磁量子数m_l决定了粒子轨道角动量在外磁场中的方向,自旋磁量子数m_s决定了粒子的自旋角动量在外磁场中的方向。
狄拉克方程式- 维基百科,自由的百科全书
https://zh.wikipedia.org/wiki/狄拉克方程式
轉為繁體網頁
狄拉克所希望建立的是一个同时具有洛伦兹协变性和薛定谔方程式形式的波方程, ... 狄拉克把这些列矢量叫做旋量(Spinor),这些旋量所决定的概率密度总是正值.轉為繁體網頁
狄拉克方程式- 維基百科,自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hant/狄拉克方程式
狄拉克所希望建立的是一個同時具有洛倫茲協變性和薛定諤方程式形式的波方程, ... 狄拉克把這些列矢量叫做旋量(Spinor),這些旋量所決定的概率密度總是正值.狄拉克符号- 维基百科,自由的百科全书
https://zh.wikipedia.org/wiki/狄拉克符号
轉為繁體網頁
狄拉克符号或狄拉克標記(英语:Dirac notation)是量子力学中广泛应用于描述量子态的一套 ... 不同的两个态矢量的内积则由一个括号来表示: \langle\phi|\psi\rangle ...轉為繁體網頁
狄拉克旋量- 维基百科,自由的百科全书
zh.wikipedia.org/wiki/狄拉克旋量
自由粒子的狄拉克方程式為: ... 是狄拉克旋量,與波向量為 \scriptstyle\vec{p} 的平面波有關,: \scriptstyle ... 為平面波的四維波向量,而 \scriptstyle\vec{p} 為任意的, ...科学网—统一路-9-从薛定谔到狄拉克- 张天蓉的博文
blog.sciencenet.cn/blog-677221-884231.html
轉為繁體網頁
2015年4月22日 - 从薛定谔到狄拉克数学物理中有许多奇妙之事,不知道是大自然本身的 ... 在上式(9-轉為繁體網頁
[PPT]4.5 狄拉克符号 - Oriyao
oriyao.com/category/p/data/kejian/4.5.ppt
轉為繁體網頁
4.5 狄拉克符号. 前面曾经指出,一个量子态相当于一个态矢量。在希尔伯特空间中选定一组基矢,即选定表象后,它可以用在这组基矢上的投影即矢量的分量表示,这 ...轉為繁體網頁
[PDF]( )y ( )1 - 物理学报
[PDF]Fig. 6.1. Schrödinger, Hilbert, and Dirac at the end of the ...
www.phy.pku.edu.cn/~qhcao/resources/class/.../hilbert.pdf
轉為繁體網頁
两个波函数的如下积分和它们傅⾥里叶变换后. 波函数的积分相等. ∫ ⇤. 1 .... 狄拉克轉為繁體網頁
[PPT]第四章矩阵力学基础- 表象理论
202.120.227.42/user/rksu/Files/Courseware/chapter4.ppt
轉為繁體網頁
... 给出用各种方式平行描述体系状态、力学量等方案--表象; 找出不同表象之间的相互关系和变换规则--么正变换; 建立一套用态矢量描述量子态的方案--Dirac ...轉為繁體網頁
狄拉克符号- 126文档分享平台 - 126文库
www.126doc.com/15750577.html
轉為繁體網頁
狄拉克符号4.5 狄拉克符号前面曾经指出,一个量子态相当于一个态矢量。在希尔伯特空间中选定一组基矢,即选定表象后,它可以用在这组基矢上的投影即矢量的分量 ...轉為繁體網頁
博文
统一路-9-从薛定谔到狄拉克  精选
精选
||
9. 从薛定谔到狄拉克
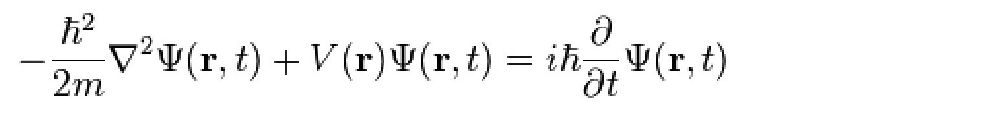

http://blog.sciencenet.cn/blog-677221-884231.html 此文来自科学网张天蓉博客,转载请注明出处。
上一篇:统一路-8-对称和守恒
下一篇:统一路-10-自旋的奥秘
数学物理中有许多奇妙之事,不知道是大自然本身的奇妙,还是因人类发现它们而奇妙,总而言之,有些概念仔细推敲起来使人目瞪口呆,无话可说,只能连呼三声:“神奇”。
如果能与外星人对话的话。你要问他们些什么问题?对工程师而言,可能会问:“你们星球是不是也用电作为主要的能源啊?”物理学家可能会用怀疑的眼光想象着他(它)们,关心他们是否是由反物质组成的?数学家们会问些什么呢?当我们将这个数学物理小文章写到此处时,最想要问的问题是:“你们是不是也用复数啊?”“你们认识这个i(-1的平方根)吗?”
A。负1的平方根
当i这个东西被法国著名哲学家及数学家笛卡儿第一次正式发明出来,并让他牵着登上了历史舞台之后,就在数学和物理理论中扮演着一个神奇的角色。欧拉在1748年发现的欧拉恒等式,更是以一种简洁奇妙的形式,将这个纯虚数与其它数学常数联系起来,令人触目惊心:
eip+1 =0。
费曼称欧拉恒等式为“数学中最奇妙的公式”,是啊,凭什么它把这5个最基本的数学常数:1、0、e、i、p,如此简洁地连系在一起?还包括了像p =3.141592653....,e =2.718281828....,这种奇怪的超越数?
到了物理学家们研究量子的年代,纯虚数i的角色就更重要了。它似乎与量子力学有着一种奇怪的渊源。我们在别的领域也使用复数,比如说,经典物理中用复数表示波动;电子工程中的各种计算,也经常使用复数而得以简化,但在那些情况,复数经常是为了方便而被引入,最后结果仍然是用实数表示。量子力学不同,复数似乎是一种少不了的,必须要用的东西。这点大概也和几何相的重要性联系在一块儿。为什么量子力学一定需要这个人为造出来的玩意儿呢?杨振宁在他的一次演讲中曾经提到过这个问题【1】。看来,这其中更深一层的奥妙,物理学的大师们也似乎还未弄清楚。
上一节中定义生成元时,也使用了这个i,其原因是为了保证生成元是厄密算符。量子理论与经典理论的一个重要区别就是物理量的算符化。在经典物理中也使用算符,比如平移算符、旋转算符等,但是,与复数的使用类似,算符对经典物理而言,是为了方便,对量子力学而言却是必须的、不可或缺的。因为在经典物理学中,诸如粒子的坐标、动量、能量、角动量等等力学量,理论上有明确的定义,实验测量有确定的数值。而在量子力学中,即使研究的是1个粒子,它的运动也需要用弥漫整个时空的波函数来描述。因此,物理量的经典概念必须加以改造方能使用,算符化便是一种改造方式。也就是说,量子理论中的物理量被作用在波函数上的算符所替代,这样更容易描述不确定性原理一类的量子规律。在量子理论的统计诠释下,每次实验测到的物理量数值不是确定的,而只是以一定几率出现的算符的本征值中的一个。
因此,这些算符的本征值应该为实数,才能在量子力学中描述与经典物理量相对应的可观测量。厄密算符便符合这个条件,厄密算符的表示矩阵是厄密矩阵,它的特点是等于自己的共轭转置矩阵,并且本征值为实数。
B。经典到量子
二十世纪初期是一个“量子英雄”辈出的年代,这与量子理论的特异性有关系。它既与经典理论迥异,又与经典理论有千丝万缕的联系。随着物理的研究深入到微观世界,发现了一个又一个不能被原有经典理论包容的物理现象,于是,这些经典理论便必须向量子理论的方向扩展,正是这些扩展,造就了一个接一个的量子英雄。
1900年,普朗克为解决经典的黑体问题而首次提出量子概念;1905年,爱因斯坦为解释经典光电效提出光量子;1913年,玻尔提出半经典原子模型;1923年,德布罗意提出物质波的概念;1924年,玻色将统计概念扩展到量子,提出玻色-爱因斯坦统计;1925年,泡利提出不相容原理; 1925年,海森堡创立矩阵力学……
量子的脚步很快就走进了1925年。这一年,薛定谔受德拜之邀在苏黎世作一个介绍德布罗意波的演讲。薛定谔的精采报告激起了听众的极大兴趣,也使薛定谔自己开始思考如何建立一个微分方程来描述这种“物质波”。这个方程一旦被建立,首先可以应用于原子中的电子上,结合波尔的原子模型,来描述氢原子内部电子的物理行为,解释索末菲模型的精细结构。
需要描述的是电子的波粒二相性,薛定谔自然首先到经典物理中寻找对应物。
电子作为经典粒子,是用牛顿定律来描述的,如何描述它的波动性呢?考察一下当时的经典力学理论,除了用牛顿力学方程表述之外,还有另外3种等效的表述方式。前面我们曾经介绍过的最小作用量原理是其中一种。除此之外,还有哈密顿原理和哈密顿-雅可比方程,这4种理论可以互相转换,都能等效地描述经典力学。
这些经典描述中,哈密顿-雅可比方程是离波动最接近的。当初,哈密顿和雅可比提出这个方程,就是为了将力学与光学作类比。
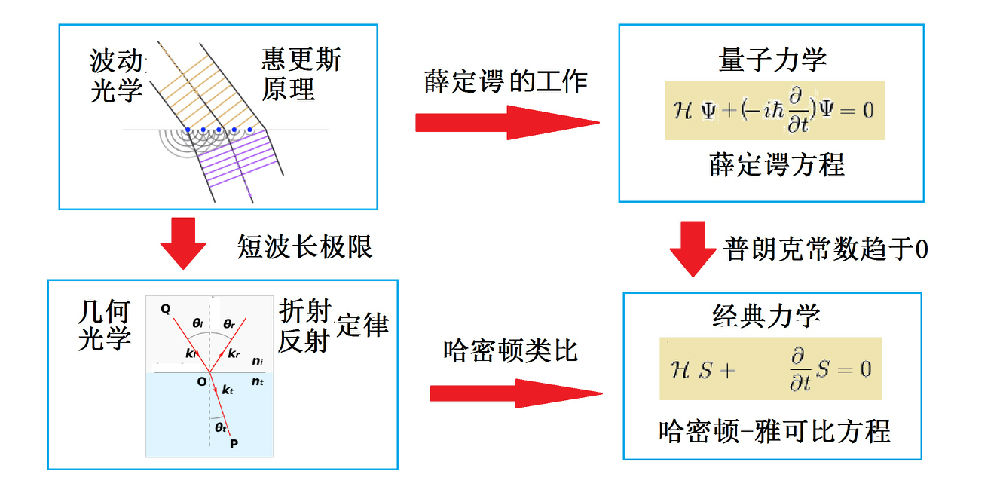
人类对“光”的认识,从来就在粒子和波动之间来回摇摆,因此,有关“光”的理论,便有几何光学和波动光学两种,分别用来描述光的粒子性和波动性。这两种描述方式并不具有等价性,而是互补的关系。几何光学不能解释光的干涉、衍射等性质,这些波动现象必须要用到波动光学的理论,但几何光学可以看作是波动光学在波长趋于零情况下的极限,见图8-1。
既然粒子与光类似,也一样具有波粒二象性,那么,类比于光线,是否能找到一个电子遵循的波动方程,使得在一定的条件下,回归到经典粒子轨道方程的情况呢?再表述得具体一点,就是说:这个波动方程的零波长极限便应该趋近于电子的经典运动方程,即哈密顿-雅可比方程。

图8-1:薛定谔方程的导出
哈密顿虽然将力学与光学进行了类比,但他并未明确地导出这样一个波动方程,这正好提供了机会,让薛定谔跟着他的思路,将上述模式运用到量子力学中而导出了薛定谔方程,并且,薛定谔用他的方程来计算氢原子的谱线,得到了与玻尔模型及实验相符合的结果【1】。
图8-1右上方和右下方,分别给出了简化的薛定谔方程和哈密顿-雅可比方程。由图中可见,从量子力学过渡到经典力学时,“零波长极限”实际上指的是普朗克常数趋于0的极限。因此,正如上一节中所说的,普朗克常数是量子化的标志。从图8-1中两个方程的比较,再一次发现了经典算符与量子算符的差别:作为时间的共轭量,量子力学算符表达式中,对时间的偏微分前面加上了一个因子(-ih(约化))。在这儿,又出现了这个神奇的负一平方根。
图8-1薛定谔方程中的H是与能量相对应的哈密顿算符。根据经典力学的能量公式:
E = p2/2m + V (9-1)
将上式中的动量p及势能V,也代之以相应的算符,可得到对应的量子力学算符方程,算符作用在电子的波函数上,也就是说,薛定谔方程可以写成以下具体形式【2】:
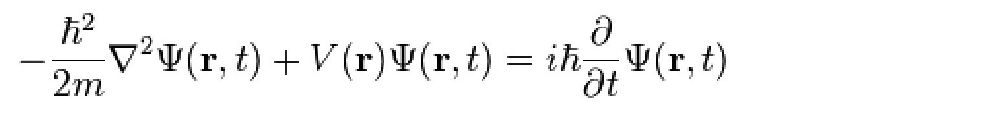
然而,因为公式(9-1)来自于经典力学,因而使得薛定谔方程有一个不足之处:它没有将狭义相对论的思想包括进去,因而只能用于非相对论的电子,也就是只适用于电子运动速度远小于光速时的情形。于是,薛定谔试图用相对论的能量动量关系:
E2 = p2c2 + m2c4 (9-2)
来构建方程。因为(9-2)的左边是E的平方,相应的算符便是对时间的2阶偏导,这实际上就是后来的克莱因-高登方程。但是,薛定谔从如此建造的方程中,没有得到令人满意的结果,还带给人们所谓负数几率的困惑。
C。狄拉克方程,算符的平方根
狄拉克敏感地意识到,薛定谔的相对论方程不成功的根源便是因为那个能量平方而带来的对时间的二阶微商。于是,狄拉克企图避免这个二阶微商,他将算符表达式(9-2)作了一个形式上的“开方”运算,并暂时令光速c=1,因此而得到:
E = Sqrt(p2c2+ m2c4)= Sqrt(p2+ m2) (9-3)
这样一来,左边变成了E的一次项,能够类似薛定谔方程那样,使用对时间的一阶微分,即使用算符(ihd/dt)来构建方程。
然后,狄拉克想了一个巧妙的办法,来处理公式(9-3)右侧根号内的量子算符。狄拉克假设这个算符表达式是另一个算符表达式的完全平方:
p2+m2 = (a1px + a2py+ a3pz + bm)2 (9-4)
在上式(9-4)右边,因为动量算符p对应的是3维空间的矢量,我们将p用它的3个算符分量px、py、pz代替,符号a1、a2、a3、b分别表示4个未知的算符。尽管普通的实数或者复数也可以看作是算符,但(9-4)中的a和b显而易见不能被表示为互相对易的实数或复数。那么,是否可以用互不对易的(n×n)矩阵来表示这几个算符呢?
在薛定谔方程中,算符是作用在电子的标量波函数y(x,t)上的,如果算符a、b等用(n×n)的矩阵表示的话,矩阵的作用对象-波函数,便应该相应地扩展成为一个n个函数的波函数矢量。当年的狄拉克是在1928年思考这些问题的,就在1年前,物理学家泡利用了3个2维矩阵,成功地描述了非相对论电子的自旋角动量。也许受到了泡利矩阵的启发,狄拉克从直觉上意识到他的方程中的a、b矩阵和泡利矩阵可能有某种关联。但是,泡利矩阵有3个,所以,狄拉克的a、b算符不应该是二维矩阵,考虑要包容3个2×2的泡利矩阵,狄拉克将他的方程中的a和b的维数定为4。如此一来,算符用4×4矩阵表示的话,狄拉克方程的解则应该是一个4个分量的函数列{y1(x,t),y2(x,t),y3(x,t),y4(x,t) }。这个列函数的性质不同于通常意义上的矢量,因而被称为旋量,详情见下一节。
于是,狄拉克将(9-4)右边的二项式展开,与等式的左边比较后,得到了他的4×4的a1、a2、a3、b矩阵必须满足的条件:
(ai)2 = b2 = I(4×4单位矩阵)
ai aj + aj ai = 0
aib + b ai = 0
上面条件中的i,j = 1、2、3。然后,狄拉克进一步找到了满足上述条件的a、b矩阵,并且导出了狄拉克方程【3】:

参考资料:
【1】张奠宙,和杨振宁漫谈:数学和物理的关系,数学传播21卷2期,1997年6月。
【2】E. Schrödinger,An Undulatory Theory of the Mechanics of Atoms and Molecules,
Phys. Rev. 28, 1049,1 December 1926
【3】Dirac, P. A. M.1928). "The Quantum Theory of the Electron". Proceedings of theRoyal Society A: Mathematical, Physical and Engineering Sciences 117 (778):610.
下一篇:自旋的奥秘
http://blog.sciencenet.cn/blog-677221-884231.html 此文来自科学网张天蓉博客,转载请注明出处。
上一篇:统一路-8-对称和守恒
下一篇:统一路-10-自旋的奥秘
26 黄永义 李德胜 郭战胜 杨荣佳 张凯军 王国强 杨波 赵国求 赵克勤 张江敏 李学忠 林中鹿 文克玲 李帅军 罗会仟 白冰 钱大鹏 应行仁 胡洪涛 xuexiyanjiu cassper hillyuan icgwang ychengwei qiue zhouguanghui
该博文允许注册用户评论 请点击登录 评论 (23 个评论)
- [23]gaoyz123
- 前人思序巧并聚,
欲引强智出奇言!
- [22]吴新忠
- 电子自旋是针对波函数的形态变化的,当然不是电子微粒本身的自转。
薛定谔的波动一元论是把微粒看成多个波函数合成的波包,自旋涉及的是一个波函数,不是合成波包的转动。
波恩的微粒一元论把波函数看成是微粒概率幅,概率幅的转动当然不是微粒的自转;
德布罗意的波-粒综合是多-多综合,一个波函数的自旋涉及是同态微粒形成的分布函数的图式转动;
爱因斯坦认为量子波不能给出微粒运动的完备信息,量子波的自旋可以与微粒的转动不一致。
- [21]钱大鹏
-

- [20]吴新忠
- 薛定谔方程给出的波函数如同无旋流体,狄拉克方程给出了具有电子自旋的波函数;广义相对论中的自由下落参照系作为局部惯性系的一个是不可以自旋与滚动的,与薛定谔波函数的无旋结构非常相似。相对论因为妙不可言而难以处理旋转问题;但是,根据德布罗意的立场,量子波函数不管是否相对论化,都不能直接描述可能具有奇点结构的微观粒子运动。
- [19]hjtvwjb
- hjtvwjb 2015-4-22 22:47
从流体力学的角度 来看,薛定谔方程就是 一个场量对时间的偏导=对流+扩散。类似于NS方程。
博主回复(2015-4-23 18:50):有道理。
==============================
我不懂量子薛定谔方程哦,你不是在讥讽我吧。
- 博主回复(2015-4-23 23:11):不是的。对不起,让你误会了。其实物理学中很多微分方程都是一定物理系统中能量(或其他)守恒定律的某种表述。薛定谔方程两边都是用算符来描述能量,流体力学中的欧拉方程也是这样的。在这个意义上,它们很类似。并且,它们描述的对象都是弥漫于空间中的某种“场”。
- [18]张磊
- 只好从头慢慢读,当年高等数学、随机数论编程还不错,多年未用全回给老师了
- [17]岳东晓
- http://blog.sciencenet.cn/blog-684007-875732.html 《为什么量子理论中必须有虚数 i》
http://blog.sciencenet.cn/blog-684007-552165.html 《科普量子力学(1)》 - 博主回复(2015-4-23 18:57):谢谢提供你的博文。
- [16]hillyuan
- 有人写过《i 的故事》之类的么?
=> Nahin, Paul (1998). An Imaginary Tale: the Story of the Square Root of −1. Princeton: Princeton University Press. - 博主回复(2015-4-23 18:56):还真有这么本书,还能下载,谢谢分享。
- [15]张磊
- 不明觉厉,应该给生物学家普及一下物理学知识
- 博主回复(2015-4-23 18:55):我觉得理论物理对生物专业的人而言,主要是因为数学少了一点,所以我的文章中讲了不少数学,如果从一开始就跟着,应该可以明白的。谢谢。
- [14]王国强
- 张老师提示的对,的确从路径积分的那个几率幅贡献的指数,作用量与h的比值,上看的更清楚。谢谢,同谢曹老师。
- [13]caozexian
- 【5】国强好。 是的,由S=klogW 出发, W是 几率Wahrscheinlichkeit首字母,也是波Welle的首字母。W=exp(S/k)
但这个表达要是波动,变量要有i,要和量子有关,就要有普朗克常数。好吧, 换成 W=exp(S/ih). 这样,S必然是作用量量纲。 S作为作用量的方程,经典力学里面现成就有,Jacobi-Hamilton 方程。 带进去,就成了薛定谔方程的样子。出锅,装盘,可以示众了。 当然,光是样子不行,重要的是这个方程用于氢原子得到了三个量子数。
【5】会仟好。 ”i"的水太深。 物理学上相当多的人没有把'i"当成物理对象对待,所以使用者多不知其威力与所以然。
- [12]caozexian
- 博主
您好。
是 Yuri Manin的Mathematics as metaphor.
所谓h趋于零,在数学上那么随口一说是可以的, 物理上它应该是个可行的操作。 短波近似,长波近似, 不必然要求涉及h的变化。关键是作为一个物理量,它应该是一个数,+ 一个单位(量纲),+它关联的物理图像。 它是一个既无左邻也无右邻的孤立存在,所谓h区域零的物理图像就不存在。 - 博主回复(2015-4-23 18:48):谢谢曹老师。
- [11]罗会仟
- 有人写过《i 的故事》之类的么?
- 博主回复(2015-4-23 18:49):还真有这样一本书,见16楼的评论。
- [10]hjtvwjb
- 从流体力学的角度 来看,薛定谔方程就是 一个场量对时间的偏导=对流+扩散。类似于NS方程。
- 博主回复(2015-4-23 18:50):有道理。

- [9]黄天翔
- 讲得非常精彩!!
- 博主回复(2015-4-23 18:46):谢谢
- [8]文克玲
- 量子力学发展史,Steven Weinberg有一个介绍。
中译本到此下载:http://blog.sciencenet.cn/blog-311388-883896.html - 博主回复(2015-4-22 21:18):太好了,很有用的资料。
- [7]陈明
- 张老师更新博客了



- 博主回复(2015-4-22 21:19):谢谢
- [6]yyy1961
- 科普性很强,赞!!!
- 博主回复(2015-4-22 21:20):谢谢
- [5]王国强
- 曹老师在2楼的意见,很有参考价值,因为他几年前在《物理》上”咬文嚼字“的时候还说谁也不知道薛定谔是怎么捣鼓出他自己的那个方程来的。看来现在他有了一个基本明确的答案了。 ^_^。。。。
我也有相同的疑问,就是在自然单位制中,c h g e 等这些”基本常数“实际上都是单位一,那么以前的很多说法,例如令 h趋向0 或让光速趋向无穷大,这些取极限的行为便得到相应的经典动力学规律的,但在自然单位制中,怎么可能取这一极限呢? 从物理上来看, 这些取极限的做法,实际上是将能量标度向0极限进行了外推。例如量子能量关系式中, hv,这两个量,既可以令h趋向于0,也可以令v趋向于0,后者实际上是玻尔的对应原理,前者是普朗克的做法,有时候也被称为”广义“对应原理的一种类型。
张老师如果能挤出时间的话,能专门写篇文章,不吝赐教就好了。 - 博主回复(2015-4-22 21:17):谢谢你的评论和建议。如何从QM过渡到CM,是一个挺有意思的问题。如果用费曼路径积分的观点来说更容易理解一些。说普朗克常数趋向0只是相对而言,常数仍然是那个常数,只是系统的尺度较大,或者说作用量数值比起h来说大得多的意思而已。很高兴和你讨论问题。
- [4]xuexiyanjiu
- 补充:
1、关于“创世--黑洞”的数学表达式——e^(iπ),其中:
(1)e——代表星系,代表费米子,或者电子(数理巧妙统一)。
(2)i——代表对宇宙历史信息或宇宙遗传性信息的数学回溯。
(3)π——代表空间信息。
2、数字1——代表“创世--宇宙中心暗物质巨球”:
也符合“道生一、一生二、二生三、三生万物”的古哲学(科学与哲学的统一)。
- [3]xuexiyanjiu
- 系列科普——点赞。
著名的欧拉方程 e^(iπ)+1 =0。
1、“费曼称欧拉恒等式为“数学中最奇妙的公式”,是啊,凭什么它把这5个最基本的数学常数:1、0、e、i、π,如此简洁地连系在一起?还包括了像π=3.141592653....,e =2.718281828....,这种奇怪的超越数?”
2、很低调的说,“暗心说网”在创建了“暗心说宇宙模型”之后,无意中发现会赋予这个欧拉方程以物理含义——“宇宙创世方程”,其中:
(1)数字0——代表宇宙初始。
数学把宇宙初始定义为0。或者说数学把宇宙万物的初始定义为0.
这是数学的简洁,也是数学的致命错误。
宇宙的初始不是0,而是“田”(在古中国文明、古印度文明、古两河文明、古希腊文明、古埃及文明中,宇宙的初始都是“田”)。
当数学强硬的以“0”代替“田”,切断了“宇宙胎儿”的来源,切断了宇宙的遗传性。
故:
虚数i,就不可避免了,它是必须的。
虚数i,是数学对客观物理实验数据进行相符合的描述、不得不引入的、其实质是对宇宙历史的“数学回溯”(宇宙历史是指:发生在数字0之前的历史,或者说是“本代宇宙大爆炸”发生之前的历史)。
(2)数字1——代表“创世--宇宙中心暗物质巨球”。
(3)e^(iπ)——代表“创世--黑洞”。
换句话说:
上述欧拉方程——“宇宙创世方程”——的具体含义是:
创世黑洞+创世宇宙中心暗物质巨球=宇宙初始。
以上,
一家之言。
欢迎质疑、讨论或分享。 - 博主回复(2015-4-22 21:20):

- [2]caozexian
- 张老师
您好。
所谓的普朗克趋于零恐是个误解。
不管用某个单位表达的普朗克常数看起来多小,它都是一个存在。 它在许多地方被当成1, 那是因为它就是1!!
可参加俄罗斯数学家、物理学家 Manin的文章关于这个问题的讨论
实际上, 薛定谔方程恰恰是选取W=exp(S/ih) 直接带入Hamilton-Jacobi 才得到的! - 博主回复(2015-4-22 21:07):是Manin Yuri吗?没有看过关于这方面的文章,能否给一个ref?
你的说法很有意思,谢谢。对这个问题我没有很多研究,但我想认为从QM到CM是h为0的极限有它的道理。一是从德布罗意波长表达式来说,它就意味着短波长近似,而是从不确定原理,h趋于0便意味着算符可对易,即回到经典力学的情况。
- [1]黄永义
- 不错!
- 博主回复(2015-4-22 21:20):谢谢
1/1 | 总计:23 | 首页 | 上一页 | 下一页 | 末页 | 跳转
|
全部作者的精选博文
全部作者的其他最新博文
全部热门博文导读
- • 记忆变成了歌
- • 诺奖得主的那几句话也叫歧视女性?
- • 得了个大奖
- • 本科生研究生入学体检要查艾滋等
- • 顽主
- • 写在毕业季——纪念博士即将毕业
No comments:
Post a Comment