k 是因為空間週期的平移對稱性所衍生出來之新的量子數，不同的 k 就對應了不同量子態的解〔k 所應該滿足的條件，以及 k 被定義的範圍

 k 是因為空間週期的平移對稱性所衍生出來之新的量子數，不同的 k 就對應了不同量子態的解〔k 所應該滿足的條件，以及 k 被定義的範圍

http://boson4.phys.tku.edu.tw/comp-solid-state/unit_band-structure_intro.htm

能帶結構簡介

單粒子能量本徵值 E 與波向量 k

量子力學以波函數（振幅的平方）來描述粒子出現在空間中的的機率分佈，而量子態的本徵能量則決定了粒子狀態或轉 移。當我們在求解薛丁格方程式時，粒子的能量本徵值與粒子的機率振幅（波函數）兩者都是最重要的待解目標。如果我們要處理的粒子是在晶體之中，亦即其所感 受到的位勢具有週期性，則 Bloch 定理告訴我們，波函數必定會具有 u_k(r)e^ik‧r 的形式，其中 u_k(r) 是在任一個晶胞裏都相同的一個週期性函數〔有關於 Bloch 定理的證明與探討，詳見教學網頁之固態物理 Ch.7〕。在此之 k 是因為空間週期的平移對稱性所衍生出來之新的量子數，不同的 k 就對應了不同量子態的解〔k 所應該滿足的條件，以及 k 被定義的範圍，亦請詳見教學網頁之固態物理 Ch.7〕。

為什麼會有這麼多 k 值，其背後的原動力就是庖利不相容原理。每個單位晶胞內的位勢一模一樣，可想見電子雲在其間的分佈情形也差不多，但一整個晶體是無數個單胞的集合體，每個 單胞內都有等數目的電子存在，但所有這些電子都不被允許具有一樣的量子態（這就是為什麼我們會用量子態是被“佔據”這種說法），要滿足這一點而且花費能量 代價最低的方法，就是利用晶體結構的延伸空間，電子要移動來形成很多組不同的 k，使它們具有不同的量子數的組合。從另一個角度來看，在整個晶體樣品的求解量子力學問題裏，以整個巨觀晶體顆粒作為邊界條件的情況之下，可以有的駐波模式就變得有非常非常多個。順帶一提，在教科書中最常見之建立 k 之量子化的方法，就是假設整個晶體樣品的一頭到另一頭接起來，可以有週期性邊界條件的成立。這看來當然有點人為，但卻能簡化了推導，重要的是只要晶胞數目 N 非常大，則樣品幾何形狀所造成之邊界條件差異就會變得很小，簡單的週期性邊界條件一樣會給出正確的結果。（一般教科書在介紹黑體幅射或者是空腔幅射的駐波態時，也使用類似的作法而採取最容易處理的邊界條件。）

在此 k 具有動量的物理意義，相當於是行進波（travaling wave） e^i(k‧r-ωt) 的波向量。事實上根據 Bloch Theorem 的結論 Ψ_k(r) = u_k(r)e^ik‧r， 而這是“與時間無關”的薛丁格方程式解，因此最完整的解的形式是 Ψ_k(r,t) = u_k(r) e^i(k‧r-ωt) ，正像是具有波向量 k 的行進波。

週期性位勢下的等效 Hamiltonian、能帶與能帶結構圖

Bloch Theorem 己經告訴我們 Ψ_k(r) = u_k(r)e^ik‧r，因此我們求解量子力學問題的目標為 u_k(r) 及Ψ_k(r) 之能量本徵值 E_n(k)，注意我們求解範圍己經簡化到只在一個晶胞之內。透過簡單的整理（把 Ψ_k(r) 代入薛丁格方程式）我們知道 u_k(r) 滿足

[ (h²/2m)(- i▽ + k)² + U(r) ] u_k(r) = E_k u_k(r)

或是

[ (- h²/2m) ( ▽² + 2ik‧▽ - k² ) + U(r) ] u_k(r) = E_k u_k(r)

上式方刮號 [ ] 裏算符的各項就是 u_k(r) 所滿足的等效 Hamiltonian，這是一個微分方程式型的本徵值問題，因此會有（無限）多組的解，以 n 標定之則其本徵值與本徵函數就會多出 n 這個指標，成為 E_n,k 與 u_n,k(r)。這個 n 我們稱之為能帶指標（Energy Band Index）。

什麼是能帶？一個能帶是由同一個能帶指標 n 及所有 k 值所構成的所有量子態的集合，這些態各有自己的 En(k) 值，但 k 相近者 E 也相近，或可說事實上 E(k) 是連續函數。（請自行查閱 k‧P 方法，它證明了：若 △k → 0，則 E(k+△k) ~ E(k)）。請記得 E(k) 是實數，因為它是 Hamiltonian （故必須是 Hermition Operator）的期望值。

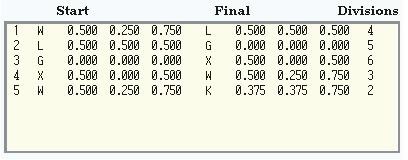
k 是分佈在布里淵區的三度空間之中，故作圖顯示 En(k) 並不容易，通常作圖時習慣取一個 k 的維度與一個 E 的維度來畫出二維的能帶結構（Band Structure）圖。實際之約定成俗的作法是選擇幾個條具較高對稱性的 k 點，前後相連成一維之路徑，再作屏風式的展開，如此一來便可在一張圖中看到多個 k 路徑上的 En(k) 圖，這就是我們常聽到的“能帶結構圖”。

 

能帶結構圖裏的對稱性與線條變化

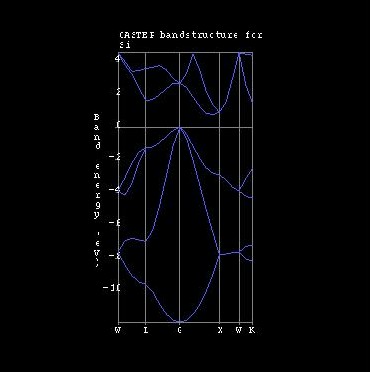
我們常有機會看到能量在能帶結構圖裏，隨著 k 的不同分裂及簡併（能量合併），這是因為我們取來畫 E(k) 的 k 值其對稱性較高，會有兩個量子態能量一模一樣的狀況發生。能帶結構的對稱性裏，有一個最普遍的，就是 E_n(k) = E_n(-k)， 它的證明很簡單〔請自行證明之〕，可在一般固態物理教科書中找到。這個性質事實上來自薛丁格方程所具有的時間反衍對稱性（Time-reversal Symmetry）。時間反衍操作在古典力學是指把所有的動量與角動量反向（例如把所有粒子的速度轉向），意即相當於是把運動方程式中時間方向反轉（變 號），請注意這並不能推廣適用於與巨觀世界的現象，故所謂的覆水難收、熵增原理與之並不衝突。由於薛丁格方程式中有這個對稱性，我們很容易就會發現 + k 與 - k 滿足的是是同一條方程式，故 E_n(k) = E_n(-k) 。在有外加磁場的情況下，薛丁格方程式並不具有時間反衍對稱性〔見 〕（我們可以想成，磁場由帶電粒子流動所產生，若粒子運動全部改為反方向，則磁場就會變號而方程式就不會是原來的方程式了。

從能帶結構看物性

電子填滿或不填滿整個能帶，對材料的物理性質有極大的影響。對金屬而言，電子填到之最高能量的地方，即費米能階，在不同的 k 方向上，費米面是由滿足 E(k) = E_F 之所有 k 點共同形成之面，通常是相當複雜的（ 這也就是為什麼計算金屬系統時 k 網格必須取得更密一點，其電荷分佈才會比較正確）。至於半導體的費米面則常定在價帶與導帶的中間。絕緣體通常不講費米面，而以價帶頂部、導帶底部、能隙等 來描述單粒子能量本徵值的位置。

金屬與絕緣體在能帶結構上最主要的差異，就是費米面的位置（對於絕對零度而言就是化學位勢），對金屬而言，費米面與能帶有相交，即存在某一條能帶有費米面通過，導致那條能帶有些 k 值有電子佔據而有些 k 值則沒有。絕緣體的能帶則是全部填滿或不填，沒有半填滿的能帶。
金屬即便在有微弱的外加電場影響下（假設電場是沿 + k 方向），仍能造成填到 + k 之態的比 - k 之態的多，如此系統會有淨電流的流動。金屬與半導體的大致區分，是溫度對其導電度的影響：基於材料之內電荷的傳導機制不同，高溫所帶來的晶格擾動造成較大的散射，使金屬的導電率降低；但高溫所造成的載子增加則促使內稟型半導體（Intrinsic Semiconductor，即不摻雜的半導體）的導電性變好。
半導體與絕緣體都有能隙，即最高佔據態到最低未佔據態之間的能量差。光學性質涉及從佔據態到未佔據態的躍遷（動量）矩陣，因此能隙大小對材料的光學性質有很大的影響。
當電子離開所佔據的量子態而躍遷到不同 k 的態，其過程就不只是能量守恆，而是連動量守恆也要滿足（光子動量轉移小，故以激發垂直躍遷為主）。從能帶之間的躍遷垂直（k 不變）與不垂直（k 會改變）來分類所需要的最低能量代價，就有所謂的直接能隙與間接能隙之分。
當物質具有磁性而我們採取所謂的“自旋極化”計算時，每條 band 不再是同時填有 spin-up 電子及 spin-down 電子，而是會各自分開成為兩條，一條只填 up spin 電子而另一條只填 down spin 電子。所填的 up 電子數與 down 電子數若有不同，則系統有淨磁矩。
 

延伸閱讀與參考資料：

有關能帶結構的重點整理，可見 Ashcroft & Mermin 第八章

k‧P 方法，見 Marder

布里淵區與費米面，見 Marder