這是 Google 對 http://www.guokr.com/blog/767808/ 的快取。 這是該網頁於 2015年5月28日 12:27:00 GMT 顯示時的快照。 在此期間,目前網頁可能已經變更。 瞭解更多資訊
提示:如要在這個網頁上快速尋找您所搜尋的字詞,請按下 Ctrl+F 鍵或 ⌘-F 鍵 (Mac),然後使用尋找列進行搜尋。
提示:如要在這個網頁上快速尋找您所搜尋的字詞,請按下 Ctrl+F 鍵或 ⌘-F 鍵 (Mac),然後使用尋找列進行搜尋。
强关联与演生规范
高温超导
量子Hall系统中演生出 规范结构与其强关联性息息相关,强关联模式的序导致了低能激发谱的有效理论正是Chern-Simons规范理论。 与量子Hall系统不太一样,高温超导的特性是通过掺杂而出现的,这可以说是看着完全不同的系统,完全不同的相态。然而它们确都有长程序,其实本质地讲它们都可以演生出规范结构的原因却是几乎一样的,这体现了凝聚态领域的第一大原理:序决定着激发。
规范结构与其强关联性息息相关,强关联模式的序导致了低能激发谱的有效理论正是Chern-Simons规范理论。 与量子Hall系统不太一样,高温超导的特性是通过掺杂而出现的,这可以说是看着完全不同的系统,完全不同的相态。然而它们确都有长程序,其实本质地讲它们都可以演生出规范结构的原因却是几乎一样的,这体现了凝聚态领域的第一大原理:序决定着激发。
一切的源头从超导系统讲起。超导现象的本质就是荷电超流体,而超流现象的本质是介种玻色子的凝聚,所以发生超导的前提以太条件是,必须存在携带电荷的玻色子。而我们知道超导材料中载流子是电子(还有代表湮灭算符的空穴),电子是费米子固然无法直接形成BEC。就如所以说,实际上超导理论的关键就在于研究合理地将原来相互作用费米子场的哈密顿量映射到玻色型平均场哈密顿量的有效理论。
历史上最早的方案是进行电子配对使得新的复合粒子是玻色子(电子都是自旋费米子,两个电子复合后总自旋就变成0或1,即自旋为整数且带 电荷的玻色子)并成为载流子;为了实现这一点,需要将电子间的作用势可以从Coulomb排斥变为有效吸引势。在固体系统中,从Hartree-Fock平均场论出发可以得到的一个重要结果是电子运动形成准粒子激发是一种带有静电屏蔽势的准电子削弱长程Coulomb作用(用Green函数理论就是计算电子自能带来的介电函数动态变化——极化);晶格振动产生元激发是声子,电子-声子作用就是Fröhlich作用,在满足一点能动量条件下电子对之间可以形成负的作用项,由Landau液体理论可知这些低能元激发作用过程都发生于费米面附近,使得费米面变得不稳定。正是这些因素使得准电子在费米面处重整形成Cooper对。现代凝聚态理论方法则是对配分函数计算的路径积分表述,使用Hubbard-Stratonovich变换后积掉费米子场自由度的办法得到有效平均场, 再以鞍点驻值方法给出自洽条件。 积掉费米子之后得到的就是BdG自洽平均场理论;并且有效场还是相变的序参量,显示的是超导系统的非对角长程序。就具体不同超导系统而言,电子之间的有效相互作用可以通过声子、磁振子、极化子、激子等等各种中间玻色子来传递,也可以通过重整化群从 裸相互作用中间逐次求出。目前的铁基超导理论就包括 磁振子BCS和泛函重整化群这样一些理论,它们都是以配对机制作为起源。
电荷的玻色子)并成为载流子;为了实现这一点,需要将电子间的作用势可以从Coulomb排斥变为有效吸引势。在固体系统中,从Hartree-Fock平均场论出发可以得到的一个重要结果是电子运动形成准粒子激发是一种带有静电屏蔽势的准电子削弱长程Coulomb作用(用Green函数理论就是计算电子自能带来的介电函数动态变化——极化);晶格振动产生元激发是声子,电子-声子作用就是Fröhlich作用,在满足一点能动量条件下电子对之间可以形成负的作用项,由Landau液体理论可知这些低能元激发作用过程都发生于费米面附近,使得费米面变得不稳定。正是这些因素使得准电子在费米面处重整形成Cooper对。现代凝聚态理论方法则是对配分函数计算的路径积分表述,使用Hubbard-Stratonovich变换后积掉费米子场自由度的办法得到有效平均场, 再以鞍点驻值方法给出自洽条件。 积掉费米子之后得到的就是BdG自洽平均场理论;并且有效场还是相变的序参量,显示的是超导系统的非对角长程序。就具体不同超导系统而言,电子之间的有效相互作用可以通过声子、磁振子、极化子、激子等等各种中间玻色子来传递,也可以通过重整化群从 裸相互作用中间逐次求出。目前的铁基超导理论就包括 磁振子BCS和泛函重整化群这样一些理论,它们都是以配对机制作为起源。
到了高温超导系统,这一切都变了。铜氧超导体的母体(未掺杂)是绝缘体,缺乏导体所具有的良好的静电屏蔽以及易变形的费米面等等特点(换言之就是费米液体失效的强关联系统——非费米液体系统),BCS配对的机制在铜氧超导体失效了。作为强关联电子结构材料的高温超导体的发现是八十年代物理学的一件大事,在这类材料发现后不久,感觉敏锐的Anderson就明确指出了高转变温度超导材料中铜氧面的重要性;并认为,应以Mott转变作为高温超导理论的出发点,因为超导电性出现在金属-绝缘体转变的附近。Anderson对相互作用费米系统的重正化群分析表明:Landau费米液体是一固定点,而Luttinger液体是另一不同的固定点。Luttinger液体一词由Haldane提出,用以界定一维量子液体的一般行为。多年前对一维排斥势Hubbard模型就已有了精确解。在Luttinger液体中,电荷与自旋具有截然不同的谱行为。Anderson指出:在所有实际的一维量子液体中,“波函数重正化因子”,这就把Landau费米液体排除在外;Landau费米液体理论之失效,并非由于在一维系统中才具有的任何特殊具体性质,而是由于其强关联在费米面上产生有限相移所致。沿此线索Anderson论证了将一维Luttinger液体推广到二维。
Pauling于1938年首先提出价键的共振理论。所谓价键态势两个自旋间配对形成单重态,在价键(VB)基础上将所有可能的自旋单重态配对波函数线性组合叠加成共振价键态。这种简并态叠加就是共振的本质,导致的结果就是离域化,也就产生分子轨道理论的效果。Anderson在针对反铁磁体的奈耳态(Neel state)和spin-peierls态的讨论中借鉴此思路提出了RVB态的新绝缘体;他认为至少在二维三角格子、自旋的反铁磁体中的反铁磁基态,可能是Bethe在反铁磁线链上提出的单重态配对(singlet)态类似体;Anderson进而提出,经高阶自能修正计算表明,诸单重态配对的移动或“共振”使其状态更稳定。Anderson在他1987年发表的论文中认为掺杂铜氧化物中超导的起源是(非超导态的)铜氧化物的莫特绝缘体特性,母化合物的绝缘态是共振价键态(RVB态)。
Mott绝缘体的物理性质可用Hubbard模型的哈密顿量来描述:

1971年,Anderson最先提出这个哈密顿量有一个非简并的基态,其中电子自旋状态是无序的。在高温超导体发现不久之后,Anderson等人提出系统存在一个共振价键基态,就是不同格点间自旋单重态线性组合:
其中 表示覆盖一个格点的最邻近的二聚态(可认为是类似Cooper对)。每一项对整体所做的贡献可认为是相同的。在平均场近似中,共振价键状态可以写成Gutzwiller投影形式,RVB态是关于BCS型函数的适当投影。这时系统的所有自旋都冻结在单重态中,构成RVB理论中的电中性真空。
表示覆盖一个格点的最邻近的二聚态(可认为是类似Cooper对)。每一项对整体所做的贡献可认为是相同的。在平均场近似中,共振价键状态可以写成Gutzwiller投影形式,RVB态是关于BCS型函数的适当投影。这时系统的所有自旋都冻结在单重态中,构成RVB理论中的电中性真空。
*然而,与BCS基态不同的是至今仍没有人对Hubbard模型或t-J模型中的哈密顿量存在这样一个超导基态进行了严格证明。
在铜氧化物晶格中,邻近铜原子相互作用形成价键
 (这里是价键中电子对算符),将它们固定在位置上。布里渊区中价键强度
(这里是价键中电子对算符),将它们固定在位置上。布里渊区中价键强度 为常数且键长分布对称分布
为常数且键长分布对称分布 , Anderson认为存在一个“赝费米面”(pseudo-Fermi surface),
, Anderson认为存在一个“赝费米面”(pseudo-Fermi surface), 在其上变号。
在其上变号。

(一种共振价键状态,其中包含邻近原子中电子的价键耦合)
对于绝缘态,每个格点均被电子占据,在RVB基态(绝缘态)由自旋子充满而形成赝费米海(PFS);而RVB基态则对应于诸自旋子充满赝费米海。按Anderson理论的观点,费米面不是电子费米海的表面,而是自旋子PFS的表面,且 不变(Luttinger液体模型)。在以少量掺杂后,当开始只有很少量二价离子(
不变(Luttinger液体模型)。在以少量掺杂后,当开始只有很少量二价离子( 等)的掺杂时,原母化合物绝缘体偏离了半填充带(pre-existing),这表示掺杂后产生了空穴子,这些空穴子很少且可能是局域化的;当掺杂量增加时,这些空穴子逐渐形成具迁移性的“气体”,还可形成自旋单重态配对,这些电子可以像Cooper对一样运动。金属化后的系统将随着掺杂而逐渐演变,最终出现超导电性。
等)的掺杂时,原母化合物绝缘体偏离了半填充带(pre-existing),这表示掺杂后产生了空穴子,这些空穴子很少且可能是局域化的;当掺杂量增加时,这些空穴子逐渐形成具迁移性的“气体”,还可形成自旋单重态配对,这些电子可以像Cooper对一样运动。金属化后的系统将随着掺杂而逐渐演变,最终出现超导电性。
我们看到了RVB相的形成对高温超导机制是至关重要的,而在强关联系统中与RVB序的形成有竞争的机制是强得多的磁有序,比如反铁磁序。随着温度降低,大多数自旋系统都会磁有序,要实现自旋液体是非常困难的。所以只有反铁磁被抑制掉,RVB才能成为基态。然而这种态实际上很难实现。Anderson再次犀利地察觉到铜离子之间的磁交换作用可能会在理论中有重要的地位。低温下破坏磁性序依靠的是阻挫(frustration)。阻挫的类型有两种,一种叫几何阻挫,一种叫动力学阻挫,几何阻挫包括加入次近邻的反铁磁耦合等等。基于高温铜氧化物与反铁磁的邻近性,邻近金属-绝缘体相变,绝缘磁相为低自旋,具二维性和载流子密度低等特点Anderson等人揭示了正是 面超交换是产生这种反铁磁耦合的一种机制——反铁磁自旋交换作用(Heisenberg模型)。
面超交换是产生这种反铁磁耦合的一种机制——反铁磁自旋交换作用(Heisenberg模型)。
回顾了高温超导理论的建立历程,我们需要更仔细地品味RVB理论所带来的深远结果。现代凝聚态物理界的大师Anderson一手开创了超导理论的新门派——分数化机制,使用了BCS理论之外的隶玻色平均场。我们从Hubbard-Anderson模型的哈密顿量出发,对电子算符作slave-boson分解后,自旋从电子上分离出去,达到玻色化的目的。也就是说电子在铜氧超导体内电子(准确地说应该是作为反粒子的空穴)分解成了一个只带自旋1/2而不携带电荷的费米子——自旋子,和一个只携带电荷 而不携带自旋的玻色子——空穴子(有的情况还有称为轨道子的元激发态);也就是与费米液体不同,这是电荷和自旋自由度明显的分开的Luttinger液体(因此这个工作也相当于把Luttinger液体理论从一维扩展到二维系统)。空穴子便可形成凝聚从而形成荷电超流体。而自旋子则组成中性费米液体——纯量子自旋液体(严格说这是RVB在理论下的图像)。总之, 高温铜氧化物超导体的母体绝缘相是RVB或量子自旋液体。RVB是一个描述自旋液体的波函数。就好像Laughlin 波函数是描述FQHE一样。这里自旋液体更强调序:拓扑序乃至量子序;而RVB给出波函数的具体结构:共振价键态。
而不携带自旋的玻色子——空穴子(有的情况还有称为轨道子的元激发态);也就是与费米液体不同,这是电荷和自旋自由度明显的分开的Luttinger液体(因此这个工作也相当于把Luttinger液体理论从一维扩展到二维系统)。空穴子便可形成凝聚从而形成荷电超流体。而自旋子则组成中性费米液体——纯量子自旋液体(严格说这是RVB在理论下的图像)。总之, 高温铜氧化物超导体的母体绝缘相是RVB或量子自旋液体。RVB是一个描述自旋液体的波函数。就好像Laughlin 波函数是描述FQHE一样。这里自旋液体更强调序:拓扑序乃至量子序;而RVB给出波函数的具体结构:共振价键态。
实际上人们从来没有在真空中看到电子的自旋电荷分离,这其实和人们从来没有看到夸克和胶子的原因一样,源于规范禁闭。电子的波函数变成了空穴子的波函数和自旋子的波函数的乘积 ,那么如果空穴子波函数改变一个相位
,那么如果空穴子波函数改变一个相位 , 而自旋子发生相反的改变
, 而自旋子发生相反的改变  ,那么电子的波函数不会发生任何变化,但是空穴子和自旋子的波函数都发生了
,那么电子的波函数不会发生任何变化,但是空穴子和自旋子的波函数都发生了 规范变换,所以这个
规范变换,所以这个 就变成一种演生的规范对称性。只有空穴子和自旋子会感受这个
就变成一种演生的规范对称性。只有空穴子和自旋子会感受这个 规范场,电子是感受不到的。那就是说自旋子和电荷子除了分别携带自旋和电荷以外,还携带一种共同的规范荷(类似电荷),它们之间通过演生的规范场是有规范相互作用的(就像电磁相互作用一样),这个规范相互作用是演生的,就像量子Hall系统演生出虚拟的
规范场,电子是感受不到的。那就是说自旋子和电荷子除了分别携带自旋和电荷以外,还携带一种共同的规范荷(类似电荷),它们之间通过演生的规范场是有规范相互作用的(就像电磁相互作用一样),这个规范相互作用是演生的,就像量子Hall系统演生出虚拟的 统计规范势;所有系统分数化都源于一种演生的规范结构。在2+1维体系中,紧致化的电磁场是有规范禁闭的,就类似3+1维时空中QCD的色相互作用一样。因此一般情况下,自旋子和空穴子会因为强烈的规范作用而禁闭成电子,而看不到分数化。人们曾经因为实验上其实测量到的是量子磁通的大小
统计规范势;所有系统分数化都源于一种演生的规范结构。在2+1维体系中,紧致化的电磁场是有规范禁闭的,就类似3+1维时空中QCD的色相互作用一样。因此一般情况下,自旋子和空穴子会因为强烈的规范作用而禁闭成电子,而看不到分数化。人们曾经因为实验上其实测量到的是量子磁通的大小 ,而认为了铜氧化物里面的的载流子是电子对 。而实际上在铜氧化物高温超导系统里面,载流子仍然是按
,而认为了铜氧化物里面的的载流子是电子对 。而实际上在铜氧化物高温超导系统里面,载流子仍然是按 量子化的,但是出现了
量子化的,但是出现了 涡旋,这样量子磁通也是
涡旋,这样量子磁通也是 。在相位弦(phase string)理论里,空穴子的
。在相位弦(phase string)理论里,空穴子的 涡旋可以自然地与个单个自旋子的统计场抵消。空穴子于自旋子之间遵循的交换统计规律则由演生的有效规范场决定,如同FQH系统。Kalmeyer和Laughlin通过比较认为,自旋子和空穴子的行为和任意子相似,服从分数统计(相对于FQH系统的统计角
涡旋可以自然地与个单个自旋子的统计场抵消。空穴子于自旋子之间遵循的交换统计规律则由演生的有效规范场决定,如同FQH系统。Kalmeyer和Laughlin通过比较认为,自旋子和空穴子的行为和任意子相似,服从分数统计(相对于FQH系统的统计角  ,高温超导里目前的机制认为其统计角为
,高温超导里目前的机制认为其统计角为  )。所以说这种自由度分离的电荷分数化机制是与配对机制完全不同一种景象,反而倒是和FQH系统相像,这一点我们将在后面一段的内容看到缘由。
)。所以说这种自由度分离的电荷分数化机制是与配对机制完全不同一种景象,反而倒是和FQH系统相像,这一点我们将在后面一段的内容看到缘由。
以上这种自由度分离分数机制只阐明了铜氧化物绝缘体如何能形成超导。那么对于其高相变温度作何解释?值得注意的是 Anderson在构造的这种二维Luttinger液体理论是基于非费米液体强电子关联效应,在高温氧化物超导体的相邻铜氧层间不存在相干的单电子隧穿而被约束于二维的 面内。尽管如此,高温氧化物超导体还存在“层间隧穿对”的超导机制,使得电子对可以在相邻铜氧层平面间经由Josephson机制相干隧穿。这种从二维到三维的跨越是一种退局域化,从而决定了高温氧化物超导电性的高临界温度
面内。尽管如此,高温氧化物超导体还存在“层间隧穿对”的超导机制,使得电子对可以在相邻铜氧层平面间经由Josephson机制相干隧穿。这种从二维到三维的跨越是一种退局域化,从而决定了高温氧化物超导电性的高临界温度 。
。
从高温超导以及更前面的量子Hall系统的讨论中,我们看到决定着规范成演生的是强关联系统形成的序。那么我们同样可以设计出特定来在演生出Chern-Simons这种拓扑规范场,这里以翁征宇一组研究的特殊晶格——超立方晶格中的强关联Mott绝缘体的 模型为范例。
模型为范例。
 是 Hubbard model 在大
是 Hubbard model 在大 (关联能很强)情形下推出的有效模型。参数J的大小正是
(关联能很强)情形下推出的有效模型。参数J的大小正是 的幂次。在半满带时
的幂次。在半满带时 退化为反铁磁体的Heisenberg模型,系统中费米子(算符)的符号则可通过Marshall符号变换(slave-fermion分解)后可规完全规范变换掉,在掺杂情形中体态符号的也可以规范变换掉, 留下纯粹的“不可约”符号结构,也就也意味着电子发生电荷-自旋自由度分离,变成空穴子和自旋子的元激发。通过在实的位形空间的运动的路径中空穴子与其自身还有与自旋子之间的交换都感生出一个
退化为反铁磁体的Heisenberg模型,系统中费米子(算符)的符号则可通过Marshall符号变换(slave-fermion分解)后可规完全规范变换掉,在掺杂情形中体态符号的也可以规范变换掉, 留下纯粹的“不可约”符号结构,也就也意味着电子发生电荷-自旋自由度分离,变成空穴子和自旋子的元激发。通过在实的位形空间的运动的路径中空穴子与其自身还有与自旋子之间的交换都感生出一个 相位的磁通,从而会在算符中出现负号。研究配分函数高温展开一直到所有阶,以及半满带中多空穴传播子还有在基态能量进行微扰展开,就会看到与正常Fermi气体系统完全不同的奇特性质。系统出现这种符号结构(sign structure)表明掺杂Mott绝缘体系统出现交换统计(mutual statistics),反映到动力学中就出现C-S项。
相位的磁通,从而会在算符中出现负号。研究配分函数高温展开一直到所有阶,以及半满带中多空穴传播子还有在基态能量进行微扰展开,就会看到与正常Fermi气体系统完全不同的奇特性质。系统出现这种符号结构(sign structure)表明掺杂Mott绝缘体系统出现交换统计(mutual statistics),反映到动力学中就出现C-S项。

凝聚态系统中,玻色子以及费米子两种统计性质截然不同的准粒子通过演生的有效规范结构中产生的分数统计,还可以通过复合结构而转化。玻色子与费米子的对应关系也意味着着凝聚态系统可以模拟出高能物理中的超对称性,甚至可能启发人们理解超对称结构背后的机制。量子Hall系统演生出的SUSY C-S 拉格朗日量:

规范结构与演生原理
从晶格上无自旋Fermi系统出发,晶格Fermi系统Hilbert空间中的态由于受到Pauli不相容原理限制,使得电子无法占据相同量子态。空间可以由各个格点费米子占有数表象基矢直积态形成的完备基张成。通过Jordan-Wigner变换,可以利用Pauli矩阵( ;它们是Bose算符)在每个格点构造一对对像是费米子算符的东西:
;它们是Bose算符)在每个格点构造一对对像是费米子算符的东西: (多格点形成就是所谓相位弦);它们可以作为对格点上的费米子进行湮灭,产生操作:占据态
(多格点形成就是所谓相位弦);它们可以作为对格点上的费米子进行湮灭,产生操作:占据态 变为
变为 空态,反之亦然。而实际上,我们通过考虑紧束缚模型的跃迁哈密顿量:
空态,反之亦然。而实际上,我们通过考虑紧束缚模型的跃迁哈密顿量:

,我们可以发现实际上随意交换各个格点间的 算符,哈密顿量作用到态矢(如前所述,这里态矢是二分量列矢)产生的结果是没有差异的,也就是
算符,哈密顿量作用到态矢(如前所述,这里态矢是二分量列矢)产生的结果是没有差异的,也就是  可以相互对易。因而实际上这两个算符相互关系虽然可以构成反对易,但实质上还是玻色子算符。Fermi Hilbert空间可以是为自旋1/2复合的硬核(hard-core:意味着不占据同一量子态)Bose Hilbert空间 (占据态,空态也可以理解为上下自旋玻色子态,而这种)。我们发现Fermi Hilbert空间中自然局域哈密顿量描述的却实际上不是Fermi系统。这样看来仅有Pauli原理依旧不够充分描述Fermi系统。如何能构造出纯粹的Fermi反对易代数,Hamiltonian的结构正好提供了解决问题的方案,从这种SU(2)代数结构出发,对跃迁矩阵结构变换为
可以相互对易。因而实际上这两个算符相互关系虽然可以构成反对易,但实质上还是玻色子算符。Fermi Hilbert空间可以是为自旋1/2复合的硬核(hard-core:意味着不占据同一量子态)Bose Hilbert空间 (占据态,空态也可以理解为上下自旋玻色子态,而这种)。我们发现Fermi Hilbert空间中自然局域哈密顿量描述的却实际上不是Fermi系统。这样看来仅有Pauli原理依旧不够充分描述Fermi系统。如何能构造出纯粹的Fermi反对易代数,Hamiltonian的结构正好提供了解决问题的方案,从这种SU(2)代数结构出发,对跃迁矩阵结构变换为 ,即是众多
,即是众多 的乘积的函数。对所以格点进行一定排序编号
的乘积的函数。对所以格点进行一定排序编号 可使得我们常见的Fermi算符出现
可使得我们常见的Fermi算符出现
 ,
,  。
。
哈密顿量就写为
 ,此处
,此处 已经与
已经与  无关。
无关。
籍此我们看到多体跃迁系统是Bose还是Fermi与Hilbert空间无关,系统的统计实际上应由哈密顿量决定。我们过去都以为自己对费米子足够了解,而凝聚态系统暗示我们要放弃还原论那种纯粹费米子,因为纯粹Fermi系统在自然界中严格来说是不存在的,可以认为玻色子比费米子更基本。费米子是可以通过玻色子的复合结构演生出现。 因为我们看到了Fermi系统的跃迁振幅是取决于所有粒子位置,是非局域量,哈密顿量实际上是高度非局域的费米子实质是非局域激发。事实上费米子不能单独存在,宇宙费米子总数是偶数,自然界揭示了费米子的行为确实很像非局域激发。近年来凝聚态物理发现的IQHE,FQH态以及拓扑序等进一步促使人们对格点规范理论以及一些自旋液体模型的研究。 自旋液体的研究直接将这方面研究带入高潮。
自旋液体的研究直接将这方面研究带入高潮。
文小刚等人发现费米子以及规范玻色子都可以从更基本的局域Bose模型演生(局域原理),这就是弦网凝聚的开端。在2+1维中基于局域Bose模型,即之前的自旋1/2硬核Bose模型,Bose算符分解为Majorana算符,通过投影构造法求解严格可解自旋模型可以产生 规范场以及非局域费米型激发。这个投影构造得到的格点量子有序态就是弦网凝聚态(和之前跃迁算符重构并所有格点排序的手续类似)。弦生成算符作用产生弦态,它由硬核Bose模型中的格点上Bose算符(Pauli算符)乘积,沿着遍历弦上所有格点形成的路径:
规范场以及非局域费米型激发。这个投影构造得到的格点量子有序态就是弦网凝聚态(和之前跃迁算符重构并所有格点排序的手续类似)。弦生成算符作用产生弦态,它由硬核Bose模型中的格点上Bose算符(Pauli算符)乘积,沿着遍历弦上所有格点形成的路径:
 (
(  )
)
则弦态一般形式为: ,这些
,这些 就是所谓的弦,它们之间相互交叉重叠的态就称为弦网态,弦网算符即为:
就是所谓的弦,它们之间相互交叉重叠的态就称为弦网态,弦网算符即为:
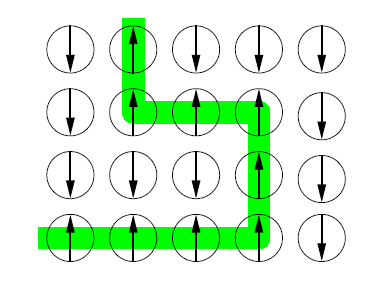
在自旋1/2硬核玻色玻色中弦网的基态凝聚可以产生 规范理论,这种低能有效理论中在晶格上会产生
规范理论,这种低能有效理论中在晶格上会产生 通量以及开弦末端的
通量以及开弦末端的 荷,
荷, 涡旋激发;开弦末端以
涡旋激发;开弦末端以 通量和
通量和 荷和涡旋 (玻色子)束缚在一起可以得到费米子。而对于3+1维,这种模型不再有效,这时以严格可解3/2自旋,和2+1维一样的投影方法,引入Majorana代数构造得到跃迁算符代数,模型的闭弦凝聚态中,开弦末端对应一个小
荷和涡旋 (玻色子)束缚在一起可以得到费米子。而对于3+1维,这种模型不再有效,这时以严格可解3/2自旋,和2+1维一样的投影方法,引入Majorana代数构造得到跃迁算符代数,模型的闭弦凝聚态中,开弦末端对应一个小 通量环路,带有能量(弦本身无能量),这 从非局域的 Majorana 费米子表示的跃迁代数在选择统计角
通量环路,带有能量(弦本身无能量),这 从非局域的 Majorana 费米子表示的跃迁代数在选择统计角 为
为 的时候也使得弦末端满足Dirac费米子跃迁代数, 形成的是服从Fermi统计准粒子激发。这一方面也可以在此清晰看到费米子是非局域的基态能量以上的准粒子激发。
的时候也使得弦末端满足Dirac费米子跃迁代数, 形成的是服从Fermi统计准粒子激发。这一方面也可以在此清晰看到费米子是非局域的基态能量以上的准粒子激发。
当给定自旋模型自由度时,可以确定局域Bose模型只有有限种类的弦网理论。比如自由度为2的时候,只有3种不同的弦网理论,其低能有效理论可以是 规范理论、
规范理论、 Chern-Simons规范理论或
Chern-Simons规范理论或 规范理论。不同的低能有效规范理论暗示了不同拓扑序。例如Z_2规范结构,基态简并度受到强拓扑保护,反映了基态非平凡拓扑序。在二维方形晶格中,边界上格点具有
规范理论。不同的低能有效规范理论暗示了不同拓扑序。例如Z_2规范结构,基态简并度受到强拓扑保护,反映了基态非平凡拓扑序。在二维方形晶格中,边界上格点具有 个简并的基态,是Majorana费米子。再进一步研究一种特殊的
个简并的基态,是Majorana费米子。再进一步研究一种特殊的 自旋立方晶格模型,将晶格的Bose自旋算符分解用Fermi表示,低能情况描述涨落集体激发具有
自旋立方晶格模型,将晶格的Bose自旋算符分解用Fermi表示,低能情况描述涨落集体激发具有 规范结构,低能有效拉格朗日量正是QED。此外理论给出了不同于对称性破缺产生保护无能隙Nambu-Goldstone激发的机制,模型中的基态不描述对称性破缺,而是具有非平凡拓扑量子序(弦网凝聚),可以导致无质量
规范结构,低能有效拉格朗日量正是QED。此外理论给出了不同于对称性破缺产生保护无能隙Nambu-Goldstone激发的机制,模型中的基态不描述对称性破缺,而是具有非平凡拓扑量子序(弦网凝聚),可以导致无质量 规范玻色子以及无质量荷电费米子(Weyl费米子,它们受到
规范玻色子以及无质量荷电费米子(Weyl费米子,它们受到 (投影对称群)保护。
(投影对称群)保护。
*量子相变和经典相变不同的是零温量子涨落产生。 不是任何对称性破缺的结果, Landau的对称性以及经典序的概念已经不适用。 因此不能再用局域序参量普适描述, 这样需要引入的是量子序。 量子序由于不是对称群能描述的,用的是 (投影对称群)。 量子相变系统基态能密度扮演经典相变中自由能的角色。 其奇点标记着量子相变, 就像经典相变是自由能的奇点来标志那样。 这时候该用什么东西替代经典的序参量? 这就是引入拓扑不变量, 以费米系统而言,这非平凡量子序就由费米面的拓扑结构来分类-- 围绕着奇点以及不围绕着奇点(就如量子Hall系统的第一陈类),还有拓扑激发的环绕数(二维XY系统发生KT相变是一种典型的拓扑序改变的例子,其中涡旋正是拓扑缺陷结构,环绕数是拓扑不变量,可衡量其准长程有序性来刻画相变) 。 这样就会再次可以量化标度量子相,代替传统的对称性决定的局域序参量,而这种拓扑是整体的。所以我们所说的量子Hall液体系统以及
(投影对称群)。 量子相变系统基态能密度扮演经典相变中自由能的角色。 其奇点标记着量子相变, 就像经典相变是自由能的奇点来标志那样。 这时候该用什么东西替代经典的序参量? 这就是引入拓扑不变量, 以费米系统而言,这非平凡量子序就由费米面的拓扑结构来分类-- 围绕着奇点以及不围绕着奇点(就如量子Hall系统的第一陈类),还有拓扑激发的环绕数(二维XY系统发生KT相变是一种典型的拓扑序改变的例子,其中涡旋正是拓扑缺陷结构,环绕数是拓扑不变量,可衡量其准长程有序性来刻画相变) 。 这样就会再次可以量化标度量子相,代替传统的对称性决定的局域序参量,而这种拓扑是整体的。所以我们所说的量子Hall液体系统以及 自旋液体系统的拓扑序可以说就是量子序的特殊情况。
自旋液体系统的拓扑序可以说就是量子序的特殊情况。
从这种局域演生原理出发去看待标准模型,我们会发现也许它就是一个边界上的低能有效理论。量子场论重整化计算就是一套低能截断的有效理论。各种参数都依赖于粒子和外界的相互作用。表现之一在于耦合常数并不是一个常数,它依赖于具体作用的动量。在电动力学里,就是电子的“有效电荷”依赖于观察这个电荷的位置,离电子越近,看到的电荷就越大,这种效应称为耦合常数的跑动。从自能修正或真空极化的图像看:电子极化周围的空间,所以离电子越远,电荷屏蔽效应越显著;离电子越近,电荷屏蔽越弱,从而看到的电子电荷就越大。然后Landau指出这套理论是不自洽的:计算重整化电荷发现,当观测距离还不等于零的时候,电子电荷已经达到了无穷(实际上Landau只是做了一级圈图计算)。所以,量子场论在一定能标上将失效,这称为Landau极点。不过目前大家相信,一个场论要么是渐近自由的,就是在无限近的距离上耦合常数为零;要么就有至少一个Landau极点。D.Gross等就证明了,QCD可以有渐进自由性质,即无论在低能标下耦合常数等于到少,它都会随着能标的增加趋于零,故没有Landau极点存在。这也被称为“存在一个紫外不动点”。这是因为除了上面提到的屏蔽效应外,由于QCD中的规范玻色子“胶子”与夸克一样携带色荷,并产生一种加强外场的反屏蔽效应,在某些条件下可以保证耦合常数在高能标下严格趋于零。所幸的是Landau极点所处在的能标远远高于我们做的能量截断,也就是超出我们有效理论的能标范围,所以对我们低能有效理论根本不造成影响。而事实上我们也只看到了真空的低能激发,这也意味着已经有很多真空对称性自发破缺了。高能物理上的这些物理图景我们不得不说在凝聚态固体系统中经常见到,几近相同。标准模型中赋予原本无能隙激发的规范玻色子质量的是Higgs机制,进而从相互作用规范场论给予无能隙费米子质量项。因此从局域玻色模型演生出无能隙费米子、规范玻色子是构建物质的第一步,在这种理论里面它们都是 保护的无能隙边缘态激发。设想我们的四维时空作为某高一维时空的边界(boundary),弦论中就有类似思想的理论:
保护的无能隙边缘态激发。设想我们的四维时空作为某高一维时空的边界(boundary),弦论中就有类似思想的理论: 。标准模型不是关于体(bulk)的理论,而是体的理论在边界上约化出的有效理论,这称谓体-边界对应(bulk-boundary correspondence);如同拓扑绝缘体系统体的强关联系统在边界上约化出C-S规范场论。如果我们的真空确实是具有一种非平凡量子序的量子比特材料 ,那么这样看来,宇宙目前的基本粒子都是边缘态的激发。而作为光传播“介质”这种意义下,真空其实就是所谓“以太”,具有拓扑序的并能低能演生出Lorentz对称性。
。标准模型不是关于体(bulk)的理论,而是体的理论在边界上约化出的有效理论,这称谓体-边界对应(bulk-boundary correspondence);如同拓扑绝缘体系统体的强关联系统在边界上约化出C-S规范场论。如果我们的真空确实是具有一种非平凡量子序的量子比特材料 ,那么这样看来,宇宙目前的基本粒子都是边缘态的激发。而作为光传播“介质”这种意义下,真空其实就是所谓“以太”,具有拓扑序的并能低能演生出Lorentz对称性。
以上我们提到“弦网理论”以及“弦理论”,两个理论名字只有一字之差,但思路却是截然不同:前者强调关系,而后者强调对象。高能物理的弦论是基于弦这个样一个对象,每条弦(world sheet)被赋予一个作用量。至于后来又有更复杂的膜理论,都是去算一个时空流形上几何对象的作用量。所以弦论这一类的理论都是面向对象的。而弦网理论中虽然也有弦这个对象,但弦不是弦网的核心。弦网是一种量子序,一种多体系统量子态集体运动模式,也可以说是量子比特编织成的关系网络。

与弦网液体理论的物理图像较接近的另一个工作是张量网理论 —— ( multi-scale entanglement renormalization ansatz;MERA是个张量网络用于量子多体理论以描述临界系统 ,由Guifré Vidal提出)处理量子多体系统。最早是Affleck于1987年发表的PRL文章,他将一组局域格点上的量子态或波函数以张量积乘起来构成矩阵积态(
( multi-scale entanglement renormalization ansatz;MERA是个张量网络用于量子多体理论以描述临界系统 ,由Guifré Vidal提出)处理量子多体系统。最早是Affleck于1987年发表的PRL文章,他将一组局域格点上的量子态或波函数以张量积乘起来构成矩阵积态( :Mtrix product states),这就是张量网络态的来源。
:Mtrix product states),这就是张量网络态的来源。

也是先从一堆客体(例如在横场Ising模型中格点上的自旋)开始,但是客体并不是核心概念,其组织关系才是。决定着张量网络的计算关键也是在于对格点编序乘积的方式,这种波函数的重整化工作在处理长程纠缠关联的量子多体系统是个十分有威力的工具。

弦网中弦不论长短以及所带什么类型激发荷,其作用量都为零(无张力),弦本身没有任何动力学,只有涨落。真正起作用的是弦的粘合联结(fusion)。以不同方粘合形成的网络就会有不同作用量。粘合方式就是一种关系,所以是关联函数决定动力学,因此弦网理论是面向关系的。因为所有的作用量都定义在粘合方式上,所以无论你怎么对弦进行微分同胚变换,只要拓扑结构不变,弦网的作用量都不会改变。所以弦网作用量是拓扑不变量。弦论中的弦被认为是最基本的物质构成,是还原的起点。而在凝聚态中,弦不是最基本的构成。就算橡胶材料中的高分子链可以视为广义上的弦网,而橡胶以及就是一种弦网凝聚态。导电橡胶的凝聚中每条聚合物链运动,那里的非定域准粒子是一种有拓扑性的畴壁(Domainwall)或称"扭结"(kink)的元激发(也就是拓扑激发)。显然它们是非定域的准粒子,(称为"孤子),而不是点粒子;就像弦的两端,成对产生和消灭。扭结或反扭结(antintik)范围非定域地分布着的电荷: ,即也是一种特定的分数荷公(但是注意,在一维空间没有分数统计)。
,即也是一种特定的分数荷公(但是注意,在一维空间没有分数统计)。

在这里,弦是由原子构成的,因此可以有丰富的内部自由度。我们可以不关心这些自由度的来源细节,认为它们都被重整化封装起来了。
量子Hall系统中演生出
一切的源头从超导系统讲起。超导现象的本质就是荷电超流体,而超流现象的本质是介种玻色子的凝聚,所以发生超导的前提以太条件是,必须存在携带电荷的玻色子。而我们知道超导材料中载流子是电子(还有代表湮灭算符的空穴),电子是费米子固然无法直接形成BEC。就如所以说,实际上超导理论的关键就在于研究合理地将原来相互作用费米子场的哈密顿量映射到玻色型平均场哈密顿量的有效理论。
历史上最早的方案是进行电子配对使得新的复合粒子是玻色子(电子都是自旋费米子,两个电子复合后总自旋就变成0或1,即自旋为整数且带
到了高温超导系统,这一切都变了。铜氧超导体的母体(未掺杂)是绝缘体,缺乏导体所具有的良好的静电屏蔽以及易变形的费米面等等特点(换言之就是费米液体失效的强关联系统——非费米液体系统),BCS配对的机制在铜氧超导体失效了。作为强关联电子结构材料的高温超导体的发现是八十年代物理学的一件大事,在这类材料发现后不久,感觉敏锐的Anderson就明确指出了高转变温度超导材料中铜氧面的重要性;并认为,应以Mott转变作为高温超导理论的出发点,因为超导电性出现在金属-绝缘体转变的附近。Anderson对相互作用费米系统的重正化群分析表明:Landau费米液体是一固定点,而Luttinger液体是另一不同的固定点。Luttinger液体一词由Haldane提出,用以界定一维量子液体的一般行为。多年前对一维排斥势Hubbard模型就已有了精确解。在Luttinger液体中,电荷与自旋具有截然不同的谱行为。Anderson指出:在所有实际的一维量子液体中,“波函数重正化因子”,这就把Landau费米液体排除在外;Landau费米液体理论之失效,并非由于在一维系统中才具有的任何特殊具体性质,而是由于其强关联在费米面上产生有限相移所致。沿此线索Anderson论证了将一维Luttinger液体推广到二维。
Pauling于1938年首先提出价键的共振理论。所谓价键态势两个自旋间配对形成单重态,在价键(VB)基础上将所有可能的自旋单重态配对波函数线性组合叠加成共振价键态。这种简并态叠加就是共振的本质,导致的结果就是离域化,也就产生分子轨道理论的效果。Anderson在针对反铁磁体的奈耳态(Neel state)和spin-peierls态的讨论中借鉴此思路提出了RVB态的新绝缘体;他认为至少在二维三角格子、自旋的反铁磁体中的反铁磁基态,可能是Bethe在反铁磁线链上提出的单重态配对(singlet)态类似体;Anderson进而提出,经高阶自能修正计算表明,诸单重态配对的移动或“共振”使其状态更稳定。Anderson在他1987年发表的论文中认为掺杂铜氧化物中超导的起源是(非超导态的)铜氧化物的莫特绝缘体特性,母化合物的绝缘态是共振价键态(RVB态)。
Mott绝缘体的物理性质可用Hubbard模型的哈密顿量来描述:
1971年,Anderson最先提出这个哈密顿量有一个非简并的基态,其中电子自旋状态是无序的。在高温超导体发现不久之后,Anderson等人提出系统存在一个共振价键基态,就是不同格点间自旋单重态线性组合:
其中
*然而,与BCS基态不同的是至今仍没有人对Hubbard模型或t-J模型中的哈密顿量存在这样一个超导基态进行了严格证明。
在铜氧化物晶格中,邻近铜原子相互作用形成价键

(一种共振价键状态,其中包含邻近原子中电子的价键耦合)
对于绝缘态,每个格点均被电子占据,在RVB基态(绝缘态)由自旋子充满而形成赝费米海(PFS);而RVB基态则对应于诸自旋子充满赝费米海。按Anderson理论的观点,费米面不是电子费米海的表面,而是自旋子PFS的表面,且
我们看到了RVB相的形成对高温超导机制是至关重要的,而在强关联系统中与RVB序的形成有竞争的机制是强得多的磁有序,比如反铁磁序。随着温度降低,大多数自旋系统都会磁有序,要实现自旋液体是非常困难的。所以只有反铁磁被抑制掉,RVB才能成为基态。然而这种态实际上很难实现。Anderson再次犀利地察觉到铜离子之间的磁交换作用可能会在理论中有重要的地位。低温下破坏磁性序依靠的是阻挫(frustration)。阻挫的类型有两种,一种叫几何阻挫,一种叫动力学阻挫,几何阻挫包括加入次近邻的反铁磁耦合等等。基于高温铜氧化物与反铁磁的邻近性,邻近金属-绝缘体相变,绝缘磁相为低自旋,具二维性和载流子密度低等特点Anderson等人揭示了正是
回顾了高温超导理论的建立历程,我们需要更仔细地品味RVB理论所带来的深远结果。现代凝聚态物理界的大师Anderson一手开创了超导理论的新门派——分数化机制,使用了BCS理论之外的隶玻色平均场。我们从Hubbard-Anderson模型的哈密顿量出发,对电子算符作slave-boson分解后,自旋从电子上分离出去,达到玻色化的目的。也就是说电子在铜氧超导体内电子(准确地说应该是作为反粒子的空穴)分解成了一个只带自旋1/2而不携带电荷的费米子——自旋子,和一个只携带电荷
实际上人们从来没有在真空中看到电子的自旋电荷分离,这其实和人们从来没有看到夸克和胶子的原因一样,源于规范禁闭。电子的波函数变成了空穴子的波函数和自旋子的波函数的乘积
以上这种自由度分离分数机制只阐明了铜氧化物绝缘体如何能形成超导。那么对于其高相变温度作何解释?值得注意的是 Anderson在构造的这种二维Luttinger液体理论是基于非费米液体强电子关联效应,在高温氧化物超导体的相邻铜氧层间不存在相干的单电子隧穿而被约束于二维的
从高温超导以及更前面的量子Hall系统的讨论中,我们看到决定着规范成演生的是强关联系统形成的序。那么我们同样可以设计出特定来在演生出Chern-Simons这种拓扑规范场,这里以翁征宇一组研究的特殊晶格——超立方晶格中的强关联Mott绝缘体的

凝聚态系统中,玻色子以及费米子两种统计性质截然不同的准粒子通过演生的有效规范结构中产生的分数统计,还可以通过复合结构而转化。玻色子与费米子的对应关系也意味着着凝聚态系统可以模拟出高能物理中的超对称性,甚至可能启发人们理解超对称结构背后的机制。量子Hall系统演生出的SUSY C-S 拉格朗日量:
规范结构与演生原理
从晶格上无自旋Fermi系统出发,晶格Fermi系统Hilbert空间中的态由于受到Pauli不相容原理限制,使得电子无法占据相同量子态。空间可以由各个格点费米子占有数表象基矢直积态形成的完备基张成。通过Jordan-Wigner变换,可以利用Pauli矩阵(
,我们可以发现实际上随意交换各个格点间的
哈密顿量就写为
籍此我们看到多体跃迁系统是Bose还是Fermi与Hilbert空间无关,系统的统计实际上应由哈密顿量决定。我们过去都以为自己对费米子足够了解,而凝聚态系统暗示我们要放弃还原论那种纯粹费米子,因为纯粹Fermi系统在自然界中严格来说是不存在的,可以认为玻色子比费米子更基本。费米子是可以通过玻色子的复合结构演生出现。 因为我们看到了Fermi系统的跃迁振幅是取决于所有粒子位置,是非局域量,哈密顿量实际上是高度非局域的费米子实质是非局域激发。事实上费米子不能单独存在,宇宙费米子总数是偶数,自然界揭示了费米子的行为确实很像非局域激发。近年来凝聚态物理发现的IQHE,FQH态以及拓扑序等进一步促使人们对格点规范理论以及一些自旋液体模型的研究。
文小刚等人发现费米子以及规范玻色子都可以从更基本的局域Bose模型演生(局域原理),这就是弦网凝聚的开端。在2+1维中基于局域Bose模型,即之前的自旋1/2硬核Bose模型,Bose算符分解为Majorana算符,通过投影构造法求解严格可解自旋模型可以产生
则弦态一般形式为:

在自旋1/2硬核玻色玻色中弦网的基态凝聚可以产生
当给定自旋模型自由度时,可以确定局域Bose模型只有有限种类的弦网理论。比如自由度为2的时候,只有3种不同的弦网理论,其低能有效理论可以是
*量子相变和经典相变不同的是零温量子涨落产生。 不是任何对称性破缺的结果, Landau的对称性以及经典序的概念已经不适用。 因此不能再用局域序参量普适描述, 这样需要引入的是量子序。 量子序由于不是对称群能描述的,用的是
从这种局域演生原理出发去看待标准模型,我们会发现也许它就是一个边界上的低能有效理论。量子场论重整化计算就是一套低能截断的有效理论。各种参数都依赖于粒子和外界的相互作用。表现之一在于耦合常数并不是一个常数,它依赖于具体作用的动量。在电动力学里,就是电子的“有效电荷”依赖于观察这个电荷的位置,离电子越近,看到的电荷就越大,这种效应称为耦合常数的跑动。从自能修正或真空极化的图像看:电子极化周围的空间,所以离电子越远,电荷屏蔽效应越显著;离电子越近,电荷屏蔽越弱,从而看到的电子电荷就越大。然后Landau指出这套理论是不自洽的:计算重整化电荷发现,当观测距离还不等于零的时候,电子电荷已经达到了无穷(实际上Landau只是做了一级圈图计算)。所以,量子场论在一定能标上将失效,这称为Landau极点。不过目前大家相信,一个场论要么是渐近自由的,就是在无限近的距离上耦合常数为零;要么就有至少一个Landau极点。D.Gross等就证明了,QCD可以有渐进自由性质,即无论在低能标下耦合常数等于到少,它都会随着能标的增加趋于零,故没有Landau极点存在。这也被称为“存在一个紫外不动点”。这是因为除了上面提到的屏蔽效应外,由于QCD中的规范玻色子“胶子”与夸克一样携带色荷,并产生一种加强外场的反屏蔽效应,在某些条件下可以保证耦合常数在高能标下严格趋于零。所幸的是Landau极点所处在的能标远远高于我们做的能量截断,也就是超出我们有效理论的能标范围,所以对我们低能有效理论根本不造成影响。而事实上我们也只看到了真空的低能激发,这也意味着已经有很多真空对称性自发破缺了。高能物理上的这些物理图景我们不得不说在凝聚态固体系统中经常见到,几近相同。标准模型中赋予原本无能隙激发的规范玻色子质量的是Higgs机制,进而从相互作用规范场论给予无能隙费米子质量项。因此从局域玻色模型演生出无能隙费米子、规范玻色子是构建物质的第一步,在这种理论里面它们都是
以上我们提到“弦网理论”以及“弦理论”,两个理论名字只有一字之差,但思路却是截然不同:前者强调关系,而后者强调对象。高能物理的弦论是基于弦这个样一个对象,每条弦(world sheet)被赋予一个作用量。至于后来又有更复杂的膜理论,都是去算一个时空流形上几何对象的作用量。所以弦论这一类的理论都是面向对象的。而弦网理论中虽然也有弦这个对象,但弦不是弦网的核心。弦网是一种量子序,一种多体系统量子态集体运动模式,也可以说是量子比特编织成的关系网络。

与弦网液体理论的物理图像较接近的另一个工作是张量网理论 ——
也是先从一堆客体(例如在横场Ising模型中格点上的自旋)开始,但是客体并不是核心概念,其组织关系才是。决定着张量网络的计算关键也是在于对格点编序乘积的方式,这种波函数的重整化工作在处理长程纠缠关联的量子多体系统是个十分有威力的工具。

弦网中弦不论长短以及所带什么类型激发荷,其作用量都为零(无张力),弦本身没有任何动力学,只有涨落。真正起作用的是弦的粘合联结(fusion)。以不同方粘合形成的网络就会有不同作用量。粘合方式就是一种关系,所以是关联函数决定动力学,因此弦网理论是面向关系的。因为所有的作用量都定义在粘合方式上,所以无论你怎么对弦进行微分同胚变换,只要拓扑结构不变,弦网的作用量都不会改变。所以弦网作用量是拓扑不变量。弦论中的弦被认为是最基本的物质构成,是还原的起点。而在凝聚态中,弦不是最基本的构成。就算橡胶材料中的高分子链可以视为广义上的弦网,而橡胶以及就是一种弦网凝聚态。导电橡胶的凝聚中每条聚合物链运动,那里的非定域准粒子是一种有拓扑性的畴壁(Domainwall)或称"扭结"(kink)的元激发(也就是拓扑激发)。显然它们是非定域的准粒子,(称为"孤子),而不是点粒子;就像弦的两端,成对产生和消灭。扭结或反扭结(antintik)范围非定域地分布着的电荷:

在这里,弦是由原子构成的,因此可以有丰富的内部自由度。我们可以不关心这些自由度的来源细节,认为它们都被重整化封装起来了。
本文由Phantom_Ghost授权(果壳网)发表,文章著作权为原作者所有。
0条评论

No comments:
Post a Comment