Ｓｕｂ－Ｐｏｉｓｓｏｎ光子统计 ，是量子光场的非经典现象之一 ，属于光场的纯量子效应 vs 散粒噪声

Ｓｕｂ－Ｐｏｉｓｓｏｎ光子统计　，是量子光场的非经典现象之一　，属于光　场的纯量子效应


．类似于３．１ 中光子反聚束效应的
讨论，表明光场量子效应的光子亚泊松分布特性也
和初始原子的纠缠这一量子特性有着直接的联系．


[PDF]杨志勇,6—光子激光的Sub—Poisson光子统计增强.渭南师专 ...

chemlab.zstu.edu.cn/ddlx/upfiles/.../201032562526489.pd...

• 頁庫存檔

轉為繁體網頁

与文献［6— 9］的结果相比，6一光子激光其光场S“6一Poisson光子统 ... 益、高损耗状态下工作时，光场将呈现非poisso￣分布的“准poisson光于统计一当激光系统 ...

 

 

散粒噪声[编辑]

维基百科，自由的百科全书

跳转至： 导航、 搜索

散粒噪声是一种实验观测中的读出噪声，当观测中数量有限的携带能量的粒子（例如电路中的电子或光学仪器中的光子）数量少到能够引发数据读取中出现可观测到的统计涨落，这种读出的统计涨落被称作散粒噪声。这种噪声在电子学、通信和基础物理领域是相当重要的概念。
这种噪声的强度随着平均电流强度或平均光强度增加，但是由于电流强度或光强度的增加会使信号本身的强度增加相对散粒噪声的增加更快，增加电流强度或光强度实际是提升了信噪比。
散粒噪声的本质在于，通过测量到的电流强度或光强度能够给出收集到的电子或光子的平均数量，但无法得知任意时刻实际收集到的电子或光子数量。实际的数量可能会高于、低于或相当于平均的数量，其分布按平均值遵循泊松分布。由于泊松分布在大量粒子数时趋向于正态分布，在大量粒子存在时信号中的散粒噪声会呈现正态分布。散粒噪声的标准差此时等于平均粒子数的平方根，信噪比从而为

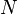这里是采集到的平均粒子数。当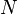很大时信噪比也会很大。因此尤其当测量中采集的粒子数很少时对散粒噪声的分析就显得非常重要。

目录

 [隐藏] 

• 1 解释
  • 1.1 直观解释
  • 1.2 电子器件中的散粒噪声
  • 1.3 量子光学中的散粒噪声
  • 1.4 引力波探测器中的散粒噪声
• 2 参见
• 3 参考文献
• 4 外部链接

解释[编辑]

直观解释[编辑]

散粒噪声的存在是由于光或电流是由处在运动中的离散的且量子化的波包构成。想像一束从激光器中出射的光照射到墙上，这束光由量子化的波包或光子构成。当照射到墙上的光斑足够亮以至于能够被肉眼直接看到时，这束光每秒钟撞击到墙上的光子可以有几十亿个。由此试想如果调低激光器的功率使光斑逐渐变得不可见，可以想象理论上能够达到使激光器中出射的光子每秒只有几个的状态。但在这里要注意，所谓“每秒只有几个光子”照射到墙上是指平均每秒照射到墙上的光子数，而量子理论指出光子从激光器中出射的时间是随机的，也就是说如果平均每秒出射光子数为5，实际出射的光子数可能在前一秒是2，下一秒是10，这样的量子涨落被称作散粒噪声。

揭示出的这种特殊的光子统计性质　，不仅深化　了人们对于光的量子本质的认识　ｔ具　

有重要的理论价值　而且还　由于这种光场　以其极低的光子数起伏在光通讯、引力波探测　、超弱信号检测　及生　

命系统的超弱光子辐射　等研　究领域显示　出了十分　广阔的应用前景，固而　使得这一研究成为　当前量子光学领　

域的一个十分活跃的前沿课题