所引入，原意是寻找这种量子态，使得坐标算符和Hamilton量算符在态平均意义上完全等同于对应的经典运动。从第二章平均值过渡的叙述可以知道，只对势函数具有不超过坐标的二阶幂次的形式，可以有解。不计一次幂的情况（这时作用力为常数），就是二次幂——谐振子的情况。因此，在谐振子的某些叠加态里可以找到这种态：这种类型的量子力学运动，在经过态平均之后，将完全等同于对应势中的经典运动相干态最初于1926年由
所引入，原意是寻找这种量子态，使得坐标算符和Hamilton量算符在态平均意义上完全等同于对应的经典运动。从第二章平均值过渡的叙述可以知道，只对势函数具有不超过坐标的二阶幂次的形式，可以有解。不计一次幂的情况（这时作用力为常数），就是二次幂——谐振子的情况。因此，在谐振子的某些叠加态里可以找到这种态：这种类型的量子力学运动，在经过态平均之后，将完全等同于对应势中的经典运动[DOC]第五章 - Quantum Physics and Quantum Information
quantum.ustc.edu.cn/old/teaching/qm2/Q5讲稿.DOC
轉為繁體網頁
利用的幺正性,. 得到等式. (5.6). 这说明，如将一个无穷小幺正算符表示为上述形式，
-
1楼 2012-08-18 19:56 简约生活-- 游戏程序员 只看Ta一点都不懂，波函数是描述波的？ 雪定谔方程只能计算波方向改变，但是不能计算波改变大小？ 咳咳，不用解释了，估计我也听不懂 :-)[0] | -
2楼 2012-08-18 21:00 zrysky 只看Ta你说的那个独立于Schrodinger方程的条件就是Hamiltonian 的厄米性[0] |
因为波函数
其中U(t)是时间演化算符。根据Schrodinger方程，U总可以表示为（假设 H不含时）
而只有当 H 是厄米算符时，才有
即 U 是幺正算符。只有 U 是幺正的，才能保证概率的守恒（即概率幅的模不变）： -
3楼 2012-08-18 21:09 Uroboros 只看Ta[0] |引用@zrysky 的话：你说的那个独立于Schrodinger方程的条件就是Hamiltonian 的厄米性
我是说，直接由薛定谔方程
因为波函数
其中U(t)是时间演化算符。根据Schrodinger方程，U总可以表示为（假设 H不含时）
而只有当 H 是厄米算符时，才有
即 U 是幺正算符。只有 U 是幺正的，才能保证概率的守恒（即概率幅的模不变）：
可以直接推出波函数的Hermitian吗？如果系统是时间独立的。。。还是说这个Hermitian是作为外界条件加上去的？不能直接由以上方程推出来？
- 5楼 2012-08-18 21:27 Uroboros 只看Ta哦~~~~我好像明白了！！！一个旋转中的矢量，如果仅仅是旋转而大小不变的话，那么对它的运动求导以后，所得导数必定是和该矢量相垂直的！。。。这样就可以解释了。。。。[0] |
- 6楼 2012-08-18 21:57 zrysky 只看Ta[0] |
引用@Uroboros 的话：我是说，直接由薛定谔方程
不可以，算符公设（力学量用线性厄米算符表示）是量子力学基本假设之一，与薛定谔方程公设独立。上面的推导对于含时的H也是一样的，只是此时的时间演化算符的形式要复杂一些。
可以直接推出波函数的Hermitian吗？如果系统是时间独立的。。。还是说这个Hermitian是作为外界条件加上去的？不能直接由以上方程推出来？
厄米性的要求来自于对力学量观测值为实数的要求，而薛定谔方程是系统的动力学方程，系统可以以其他动力学方程演化，如Dirac 方程，但力学量的厄米性却仍然要保证。现在也有pesudo-hermitian quantum mechanics， 就是对算符公设进行了扩展 - 7楼 2012-08-18 22:11 Uroboros 只看Ta[0] |
引用@zrysky 的话：不可以，算符公设（力学量用线性厄米算符表示）是量子力学基本假设之一，与薛定谔方程公设独立。上面的推导对于含时的H也是一样的，只是此时的时间演化算符的形式要复杂一些。
哦。。。原来是这样。。。话说回来，是因为能量算符H本身就是具有Hermitian的，所以那个方程才能保持概率幅的模不变。。。谢谢你！我明白了~
厄米性的要求来自于对力学量观测值为实数的要求，而薛定谔方程是系统的动力学方程，系统可以以其他动力学方程演化，如Dirac 方程，但力学量的厄米性却仍然要保证。现在也有pesudo-hermitian quantum mechanics， 就是对算符公设进行了扩展
-
8楼 2012-08-18 22:12 浔荆 只看Ta看的晕晕乎乎的、、、没抓住要点。不过你在3楼给出的薛定谔方程只是自由粒子的方程，势场以及自旋等更多的变量没有考虑在内。事实上不同情况下粒子满足的薛定谔方程是不一样的。一般一维粒子的薛定谔方程表达为[0] |
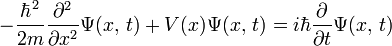
求解薛定谔方程时，第一步就是要根据系统的性质（维度、势场、采用的坐标、自旋等）来确定哈密顿算符，其次才能求解薛定谔方程， - 9楼 2012-08-18 22:18 Uroboros 只看Ta[0] |
引用@浔荆 的话：看的晕晕乎乎的、、、没抓住要点。不过你在3楼给出的薛定谔方程只是自由粒子的方程，势场以及自旋等更多的变量没有考虑在内。事实上不同情况下粒子满足的薛定谔方程是不一样的。一般一维粒子的薛定谔方程表达为
求解薛定谔方程时，第一步就是要根据系统的性质（维度、势场、采用的坐标、自旋等）来确定哈密顿算符，其次才能求解薛定谔方程，
谢谢你，我不是要求解薛定谔方程，所以把情况都简化了，连势场都没考虑。。。我只是在想直接由这种一维粒子的薛定谔方程能否反推出H是Hermitian的。。。不过目前问题已经解决了。。。 - 10楼 2012-08-18 22:48 zrysky 只看Ta[0] |
引用@Uroboros 的话：哦~~~~我好像明白了！！！一个旋转中的矢量，如果仅仅是旋转而大小不变的话，那么对它的运动求导以后，所得导数必定是和该矢量相垂直的！。。。这样就可以解释了。。。。
虽然LZ应该已经明白了，但还是说一下吧，仅就这句话来说，矢量的这个结论并不适用于量子力学。因为设矢量空间的内积定义为
因为
所以
而只有内积是定义在实数域上时，才有
即你说的矢量的变化率与矢量垂直。而量子力学中的内积是定义在复数域上的，把换成
因此只能得出
若这里导数与矢量垂直成立，因为正比与
的导数，那么应该有
那么概率守恒得出系统的能量恒为零 - 11楼 2012-08-18 22:53 Uroboros 只看Ta[0] |
引用@gaoyc 的话：一点都不懂，波函数是描述波的？ 雪定谔方程只能计算波方向改变，但是不能计算波改变大小？ 咳咳，不用解释了，估计我也听不懂 :-)
好吧。。。确实不好解释。。。因为那个波不是普通的波~~~那被称为概率波。。。如果有什么直观的方式可以理解这个的话，那就是以太了（虽然说这个词会被打脸，但是我实在找不到什么东西可以作为这种波的载体了。。。。
） - 12楼 2012-08-18 22:59 Uroboros 只看Ta[0] |
引用@zrysky 的话：虽然LZ应该已经明白了，但还是说一下吧，仅就这句话来说，矢量的这个结论并不适用于量子力学。因为设矢量空间的内积定义为
因为
所以
而只有内积是定义在实数域上时，才有
即你说的矢量的变化率与矢量垂直。而量子力学中的内积是定义在复数域上的，把换成
因此只能得出
若这里导数与矢量垂直成立，因为正比与的导数，那么应该有
那么概率守恒得出系统的能量恒为零
你没理解我的意思。。。我是把波函数本身在空间上某点的取值看做关于时间的复数矢量——就是在一维空间轴上某点为原点取一个垂直的复平面，然后看该点的波函数取值，就应该是这个平面中的一个矢量，该矢量最终会随着时间的变化而旋转，但是大小始终不变。。。。这应该就是薛定谔方程的含义。。。。 - 15楼 2012-08-19 00:09 zrysky 只看Ta[0] |
引用@Uroboros 的话：
你是指某个固定坐标点的波函数，把函数值当作复平面上的矢量（保持坐标点不变）对吧？
你没理解我的意思。。。我是把波函数本身在空间上某点的取值看做关于时间的复数矢量——就是在一维空间轴上某点为原点取一个垂直的复平面，然后看该点的波函数取值，就应该是这个平面中的一个矢量，该矢量最终会随着时间的变化而旋转，但是大小始终不变。。。。这应该就是薛定谔方程的含义。。。。
如果你是这个意思，那你的问题本身都是有问题的，即根本就不存在什么概率幅的大小不变，时间演化过程中某一个基上的分量是完全可以随时间变化的（波函数就是态矢量在坐标表象坐标本征态上投影的分量），守恒的只是总的概率，而不是在每个基上的概率分布。除非你用能量本征态对态矢量进行分解，由于每一个基都是一个定态，才有处在每个本征态上的概率不随时间变化。
而只有态矢量处于定态时，才有概率关于坐标的分布不随时间变化 - 16楼 2012-08-19 02:03 Uroboros 只看Ta[0] |
引用@zrysky 的话：你是指某个固定坐标点的波函数，把函数值当作复平面上的矢量（保持坐标点不变）对吧？
确实如此，所以我才用的那个关于能量的方程（H算符取粒子动能），这样H就是Hermitian的，因此可以保证每个基都是定态，概率不随时间变化，概率幅只改变方向不改变大小。。。。话说回来，还是因为我选的Hamilton算符是能量算符，所以才具有这种特性的，并不是薛定谔方程本身导致的。。。。嗯，我已经明白了，感谢你的详解！
如果你是这个意思，那你的问题本身都是有问题的，即根本就不存在什么概率幅的大小不变，时间演化过程中某一个基上的分量是完全可以随时间变化的（波函数就是态矢量在坐标表象坐标本征态上投影的分量），守恒的只是总的概率，而不是在每个基上的概率分布。除非你用能量本征态对态矢量进行分解，由于每一个基都是一个定态，才有处在每个本征态上的概率不随时间变化。
而只有态矢量处于定态时，才有概率关于坐标的分布不随时间变化 -
17楼 2012-08-19 09:57 EPOLISODA 只看Ta[0] |引用@Uroboros 的话：
你没理解我的意思。。。我是把波函数本身在空间上某点的取值看做关于时间的复数矢量——就是在一维空间轴上某点为原点取一个垂直的复平面，然后看该点的波函数取值，就应该是这个平面中的一个矢量，该矢量最终会随着时间的变化而旋转，但是大小始终不变。。。。这应该就是薛定谔方程的含义。。。。
感觉lz这个理解有问题啊- - 。。。。薛定谔方程含义是能量守恒。。。况且希尔伯特空间也不能类比复空间， 谈论态矢量的“方向”感觉怪怪的~ - 18楼 2012-08-19 16:23 Uroboros 只看Ta[0] |
引用@EPOLISODA 的话：
额。。。我确实没表达清楚。。。因该是将态矢量分解到一组本征态构成的基下面，然后进行观察。。。这个时候在这组基下的坐标是复数的，然后看这个复数的方向。。。并不是看态矢量的方向——毕竟态矢量是希尔伯特空间中的函数，如果不确定基的话，很难说有什么方向。。。。
感觉lz这个理解有问题啊- - 。。。。薛定谔方程含义是能量守恒。。。况且希尔伯特空间也不能类比复空间， 谈论态矢量的“方向”感觉怪怪的~ - 19楼 2012-08-19 18:10 EPOLISODA 只看Ta[0] |
引用@Uroboros 的话：额。。。我确实没表达清楚。。。因该是将态矢量分解到一组本征态构成的基下面，然后进行观察。。。这个时候在这组基下的坐标是复数的，然后看这个复数的方向。。。并不是看态矢量的方向——毕竟态矢量是希尔伯特空间中的函数，如果不确定基的话，很难说有什么方向。。。。
哈~ lz说的就是波函数的相位啊。。。确实一般情况下，薛定谔方程解出的波函数可以添加一个任意的相位因子。。。也就是lz说的旋转了~ - 20楼 2012-08-19 18:19 Uroboros 只看Ta[0] |
引用@EPOLISODA 的话：
对的。。。就是这个意思。。。总算表达清楚了。。。
哈~ lz说的就是波函数的相位啊。。。确实一般情况下，薛定谔方程解出的波函数可以添加一个任意的相位因子。。。也就是lz说的旋转了~
。。。。果然用语言来描述数学现象是十分艰难的事情——头脑中的图像、公式。。。转变成语言后就变成两外一回事了。。。。 - 21楼 2012-08-19 19:04 EPOLISODA 只看Ta[0] |
引用@Uroboros 的话：对的。。。就是这个意思。。。总算表达清楚了。。。。。。。果然用语言来描述数学现象是十分艰难的事情——头脑中的图像、公式。。。转变成语言后就变成两外一回事了。。。。
所以我才真心觉得，做科普的才是真正的大师啊 -
22楼 - 23楼 2012-08-20 14:31 Uroboros 只看Ta[0] |
引用@Dtsio 的话：波函数可以理解为Hilbert空间中的态矢量在坐标表象下的表达式。
你是说这个吗？：
|ψ>=c1|φ1>+c1|φ1>+c2|φ2>+c3|φ3>+c4|φ4>+。。。。 - 24楼 2012-08-20 14:35 DTSIo 只看Ta[0] |
引用@Uroboros 的话：你是说这个吗？：
不是，我想说它是一个跃迁矩阵元。态矢量和坐标算符本征矢量的内积。
|ψ>=c1|φ1>+c1|φ1>+c2|φ2>+c3|φ3>+c4|φ4>+。。。。 - 25楼 2012-08-20 14:39 DTSIo 只看Ta[0] |
引用@Uroboros 的话：你是说这个吗？：
坐标算符有连续的本征值谱，这样每个本征矢和态矢量的跃迁矩阵元之间的内积都是个数，每个坐标算符本征矢对应一个数，也就是每个座标对应一个数，就是波函数了。因为每个跃迁矩阵元是个概率幅，应用哥本哈根阐释也就知道了这代表粒子在这点出现的概率幅。
|ψ>=c1|φ1>+c1|φ1>+c2|φ2>+c3|φ3>+c4|φ4>+。。。。 - 26楼 2012-08-20 14:51 Uroboros 只看Ta[0] |
引用@Dtsio 的话：坐标算符有连续的本征值谱，这样每个本征矢和态矢量的跃迁矩阵元之间的内积都是个数，每个坐标算符本征矢对应一个数，也就是每个座标对应一个数，就是波函数了。因为每个跃迁矩阵元是个概率幅，应用哥本哈根阐释也就知道了这代表粒子在这点出现的概率幅。
不太明白。。。能用公式表达一下吗？？？ - 27楼 2012-08-20 18:26 DTSIo 只看Ta[0] |
引用@Uroboros 的话：不太明白。。。能用公式表达一下吗？？？
不好意思刚才用的iPad很难打。
其实抽象的态矢量|1>,|2>之类的不太好说明问题.不过有处理方法.想象位置算符X,它有连续的本征值谱,它的本征值可以是任何一个空间点.用|x>来代表具有本征值x的那个本征向量.现在假设已经根据定态薛定谔方程求出了哈密顿的各个本征向量,如果它们是完备的那么就可以建立能量表象的各个基,可以记成|0>,|1>,|2>...然后求内积:<x|n>,这就是哈密顿的第n个本征态向"粒子出现在x处"这一事件跃迁的跃迁振幅,是个数,因为每个x对应一个振幅,这也就是波函数了.所以不能按照经典的"大小方向"来理解它,虽然可以这么做类比吧.如果要类比经典矢量的话,那么哈密顿算符就是某种转动吧.
我觉得我有点答非所问?好吧,我的理解是,之所以谈"波函数",是因为概率振幅<x|n>的表达式同经典波的表达式很相像,当然可以谈"相位".而之所以有粒子性,还是因为哈密顿的本征值不连续,这就好像是n个带有一定能量的粒子一样. - 28楼 2012-08-20 19:11 Uroboros 只看Ta[0] |
引用@Dtsio 的话：不好意思刚才用的iPad很难打。
位置算符不是已经有了吗：Xφ(x)=xφ(x)啊。。。它的本征值不就是它的空间坐标么？。。。哦~~~我懂你的意思了，你一直在用“跃迁”这个词，一开始没看懂，不过这不就是做投影么。。。话说算速度的时候也是这么处理的，只不过是往标准的螺线上做投影（每个螺线对应一个本征态和一种速度）。。。。额~就是傅里叶变换。。。你懂的。。。。
其实抽象的态矢量|1>,|2>之类的不太好说明问题.不过有处理方法.想象位置算符X,它有连续的本征值谱,它的本征值可以是任何一个空间点.用|x>来代表具有本征值x的那个本征向量.现在假设已经根据定态薛定谔方程求出了哈密顿的各个本征向量,如果它们是完备的那么就可以建立能量表象的各个基,可以记成|0>,|1>,|2>...然后求内积:<x|n>,这就是哈密顿的第n个本征态向"粒子出现在x处"这一事件跃迁的跃迁振幅,是个数,因为每个x对应一个振幅,这也就是波函数了.所以不能按照经典的"大小方向"来理解它,虽然可以这么做类比吧.如果要类比经典矢量的话,那么哈密顿算符就是某种转动吧.
我觉得我有点答非所问?好吧,我的理解是,之所以谈"波函数",是因为概率振幅<x|n>的表达式同经典波的表达式很相像,当然可以谈"相位".而之所以有粒子性,还是因为哈密顿的本征值不连续,这就好像是n个带有一定能量的粒子一样. -
29楼 2012-08-20 19:59 Ryne_exp618 只看Ta[0] |引用@zrysky 的话：你说的那个独立于Schrodinger方程的条件就是Hamiltonian 的厄米性
就一个问题。亲，你是如何在guokr输入LaTeX的？
因为波函数
其中U(t)是时间演化算符。根据Schrodinger方程，U总可以表示为（假设 H不含时）
而只有当 H 是厄米算符时，才有
即 U 是幺正算符。只有 U 是幺正的，才能保证概率的守恒（即概率幅的模不变）： - 31楼 2012-08-20 20:52 zrysky 只看Ta[0] |
引用@exp618 的话：就一个问题。亲，你是如何在guokr输入LaTeX的？
以输入图片格式输入图片链接
http://latex.codecogs.com/png.latex?后面加上latex代码即可 - 32楼 2012-08-20 20:56 zrysky 只看Ta[0] |
引用@Uroboros 的话：位置算符不是已经有了吗：Xφ(x)=xφ(x)啊。。。它的本征值不就是它的空间坐标么？。。。哦~~~我懂你的意思了，你一直在用“跃迁”这个词，一开始没看懂，不过这不就是做投影么。。。话说算速度的时候也是这么处理的，只不过是往标准的螺线上做投影（每个螺线对应一个本征态和一种速度）。。。。额~就是傅里叶变换。。。你懂的。。。。
不是，态矢量是希尔伯特空间中抽象的矢量，而波函数是坐标表象下以坐标本征态为基进行展开后的分量。但坐标本征矢量是连续谱，所以用
- 33楼 2012-08-20 21:23 Uroboros 只看Ta[0] |
引用@zrysky 的话：不是，态矢量是希尔伯特空间中抽象的矢量，而波函数是坐标表象下以坐标本征态为基进行展开后的分量。但坐标本征矢量是连续谱，所以用展开波函数得到的系数是一个连续的函数，即波函数：
哦。。。是这样。。。我原来一直把波函数和态矢量当成一回事了。。。。。。。毕竟有两个薛定谔方程，一个是直接用态矢表示的，另一个是直接用波函数表示的。。。。所以有点混淆~~~ - 34楼 2012-08-20 22:26 DTSIo 只看Ta[0] |
引用@zrysky 的话：不是，态矢量是希尔伯特空间中抽象的矢量，而波函数是坐标表象下以坐标本征态为基进行展开后的分量。但坐标本征矢量是连续谱，所以用展开波函数得到的系数是一个连续的函数，即波函数：
嗯,同意.正解. - 35楼 2012-08-20 22:27 DTSIo 只看Ta
引用@Uroboros 的话：哦。。。是这样。。。我原来一直把波函数和态矢量当成一回事了。。。。。。。毕竟有两个薛定谔方程，一个是直接用态矢表示的，另一个是直接用波函数表示的。。。。所以有点混淆~~~
zrysky 正解.就是这个意思.我有点答非所问?
No comments:
Post a Comment