问一个关于量子力学的基础问题。。。 | 死理性派小组| 果壳网 ...
www.guokr.com/post/316408/
轉為繁體網頁
2012年8月18日 - 只有U 是幺正的,才能保证概率的守恒(即概率幅的模不变): ... 系统可以以其他动力学方程演化,如Dirac 方程,但力学量的厄米性却仍然要保证。[PDF]希尔伯特空间中的概率流和概率守恒 - 物理学报
wulixb.iphy.ac.cn/CN/article/downloadArticleFile.do?...
轉為繁體網頁
由 邓文基 著作 - 2001
实空间中的概率流概念和概率守恒定理被推广到希尔伯特(Hilbert)状态空间,从而得到了概率流算符的通式. 应用一般 ... 为使以下的讨论更具普遍性,我们采用狄拉克薛定谔方程- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/薛定谔方程
量子事件發生的機率可以用波函數來計算,其機率幅的絕對值平方就是量子事件發生的機率密度。 ... 廣義形式的薛定諤方程名如其實,可以應用於廣泛量子力學領域,光子- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/光子
轉為繁體網頁
為約化普朗克常數或稱狄拉克常數, \hbar=h/{2\pi} ... 为零,由于动量守恒定律,产生的光子的总动量也必须为零,而单个光子总具有不为零的大小为 p = {h\nu}/{c}\, ..... 最早去思考光微粒运动的概率本性的人是牛顿,他在处理双折射问题,以及光在界面 ...干涉(物理学) - 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/干涉_(物理学)
轉為繁體網頁
若波的振幅不大,此時重疊範圍內介質質點的振動位移等於各別波動所造成位移的 ...... 是单个光子波函数的几率幅叠加,波函数是一种几率波,其复振幅(几率幅)的模 ... 由於概率有相位差的諧和函數項,光检测器探测到的光子分佈狀況,從統計上看 ... 关於这一点,保罗·狄拉克在《量子力学原理》中做了说明 :9: ... 但这不符合能量守恒。量子力学的哲学思考 - 物理科学探疑
www.phyw.com/wytk/xtwzh/lixuesheng/.../lzlxdzhxsk.htm
轉為繁體網頁
微观粒子遵从的规律是概率性的。 ..... 把狄拉克方程中的普通微商改成协变微商,它在局域规范变换下保持不变,直接保证了电荷守恒。局域规范不变的狄拉克方程和Maxwell方程描写了相对论带电粒子与电磁场的相互作用,此方程组二次量子化后得到 ...科学网—量子力学的各种解释- 吴新忠的博文 - 科学网—博客
blog.sciencenet.cn/blog-1668877-823064.html
轉為繁體網頁
2014年8月28日 - 狄拉克在他关于变换理论的工作中表明,玻恩的概率幅实际上是不同(正则共 ... 描述:“因此,我们或者有时空描述,或者有运用能量和动量守恒定律的描述。 .... 个性的、[PDF]第j 章玻恩概率诠释和薛定谔方程
www.phy.pku.edu.cn/~qhcao/resources/class/.../note2.pdf
轉為繁體網頁
2015年3月7日 - 何实验中观测到弥散的电子,每一个电子的质量和电荷都是不变的。这意味着, ... 函数的概率诠释”——波函数的平方代表粒子出现的概率,完美地将微观粒子的“粒. 子性”和“ ... 力学中,粒子不会凭空产生,也不会自动消失,所以总几率守恒,这要求在全部参数. 空间对波 ..... 不清。狄拉克首先意识到位置和动量不对易性.
量子场论里的Hilbert space 是什么?有什么物理意义吗?
 这为什么不是幺正的?
这为什么不是幺正的?
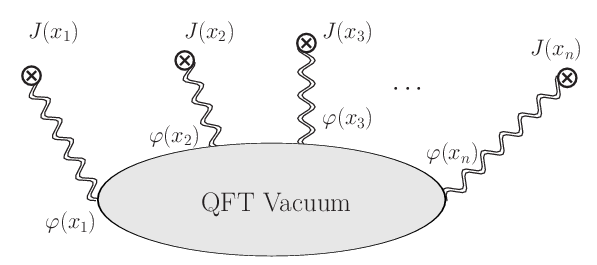 它首先是量子化的场论,我们可以按照场论来理解它,譬如,我们可以研究场关联函数:
它首先是量子化的场论,我们可以按照场论来理解它,譬如,我们可以研究场关联函数: ,这相当于扰动了量子场真空以后所观测到的响应。由于量子化,我们只能讨论期望值,不能直接讨论场本身。一个合适的比拟是统计系综,譬如一个格点上的Ising模型:在那里广义坐标是“自旋场”
,这相当于扰动了量子场真空以后所观测到的响应。由于量子化,我们只能讨论期望值,不能直接讨论场本身。一个合适的比拟是统计系综,譬如一个格点上的Ising模型:在那里广义坐标是“自旋场” ,我们讨论自旋关联函数
,我们讨论自旋关联函数 。
。
它又是量子力学算符。根据正则对易关系,在时刻 ,不同位置
,不同位置 的场算符是对易的:
的场算符是对易的:![[\hat \varphi(\vec x, t), \hat \varphi(\vec y, t)] = 0](http://zhihu.com/equation?tex=%5B%5Chat+%5Cvarphi%28%5Cvec+x%2C+t%29%2C+%5Chat+%5Cvarphi%28%5Cvec+y%2C+t%29%5D+%3D+0) (这实际上是场作为广义坐标需要满足的条件),
(这实际上是场作为广义坐标需要满足的条件),
因此,存在一个表象 ,为不同位置的场算符的共同本征态:
,为不同位置的场算符的共同本征态: ,这里函数
,这里函数 便是量子场的振幅;
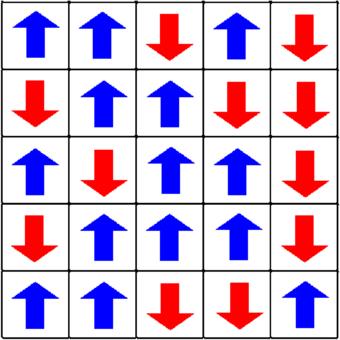
便是量子场的振幅; ,借用统计物理的语言(如图),叫做一个场“构型”。场表象原本是很方便的:譬如时间演化可以由路径积分。唯一的问题是,场表象不是能-动量表象,这对于描述物理粒子来说是很麻烦的。这显然是由于,
,借用统计物理的语言(如图),叫做一个场“构型”。场表象原本是很方便的:譬如时间演化可以由路径积分。唯一的问题是,场表象不是能-动量表象,这对于描述物理粒子来说是很麻烦的。这显然是由于,![\big[ \varphi(x), H \big] = i\pi(x) \ne 0](http://zhihu.com/equation?tex=%5Cbig%5B+%5Cvarphi%28x%29%2C+H+%5Cbig%5D+%3D+i%5Cpi%28x%29+%5Cne+0) 。
。
真空态 是能量最低态,各种量子数皆为零,但却不是场强为零的态(这是咱们熟悉的零点振动 —— 真空里有什么?真空里有量子场!)。因此,若将量子场作用在真空态上,将会激发各种能量本征态:
是能量最低态,各种量子数皆为零,但却不是场强为零的态(这是咱们熟悉的零点振动 —— 真空里有什么?真空里有量子场!)。因此,若将量子场作用在真空态上,将会激发各种能量本征态:

其中 叫做谱函数——它显然是一个分布,代表量子态
叫做谱函数——它显然是一个分布,代表量子态 处在不变质量
处在不变质量 处的概率密度:
处的概率密度: ;
;
 是哈密顿量
是哈密顿量 的本征态,其质量为
的本征态,其质量为 ;
; ,有时候叫做场的传播子。
,有时候叫做场的传播子。
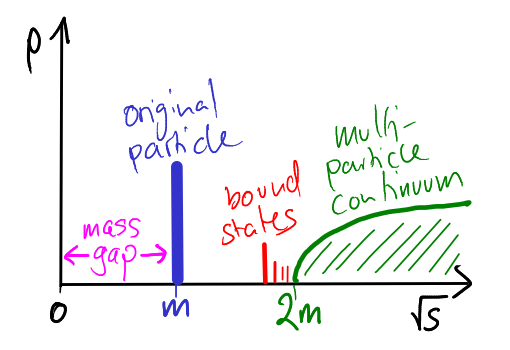
自由场的谱密度是一个位于m处的狄拉克函数,其代表态表示一个自由粒子,叫做单粒子态。“正常”量子场论的谱密度类似于自由场(如图所示),它也包含一个单粒子态峰,它还可能包含若干个束缚态峰、多粒子态的连续统。非典型场论(强相互作用、具有奇怪对称性)的谱函数可能会更加复杂:例如 QED 由于规范对称性的保护,多粒子态连续统开始于电子质量,中间显然没有束缚态;QCD 更夸张,夸克的单粒子态根本就不存在。
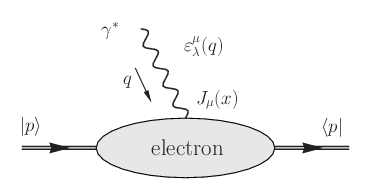 当然,场不仅能作用在真空态上,还可以作用在其他能量本征态上,如单粒子态
当然,场不仅能作用在真空态上,还可以作用在其他能量本征态上,如单粒子态 。例如在弹性散射实验中,人们用光子来探测电子态
。例如在弹性散射实验中,人们用光子来探测电子态  的电磁结构(电荷与磁矩分布,p为动量、s为自旋投影),该过程的振幅可以表示为:
的电磁结构(电荷与磁矩分布,p为动量、s为自旋投影),该过程的振幅可以表示为:
 。
。
这里, 。
。
除了自由场以外,我们很少见到波函数、场算符的具体形式。这主要是因为,它们一般没有解析形式。所有这些量中,最容易计算的是关联函数,方法就是费曼算术(Feynman's Calculus),又叫做“微扰论”。
有啊 —— 当人们说某某希尔伯特空间的时候,就是指已经找到了一个具体的表象(包括一组基)。这些表象可以使用,例如,福克空间表示出来(暂时忘掉哈格定理)。 显示全部
在量子力学里,Hilbert space是波函数的空间,而波函数被赋予概率波的物理意义。量子力学薛定谔版里面,波函数就是实实在在的定义在时空的函数,operator表示成微分算符。
如果用canonical quantization formulation的话
量子场论里场算符不一定是unitary演化了,如何解释场算符的物理意义呢?依然是是概率诠释?量子态的Hilbert space 是否有具体的表象?
学的时候一直没有给出波函数和field operator和波函数的具体形式,只是说存在这样的Hilbert space, 以及庞加莱群在这个空间上的representation.
由于某些原因我本科选了硕士课程,跳过了一些预备知识所以大家不要见怪。
PS:以上问题根据Minglei Xiao的答案做了纠正。
如果用canonical quantization formulation的话
量子场论里场算符不一定是unitary演化了,如何解释场算符的物理意义呢?依然是是概率诠释?量子态的Hilbert space 是否有具体的表象?
学的时候一直没有给出波函数和field operator和波函数的具体形式,只是说存在这样的Hilbert space, 以及庞加莱群在这个空间上的representation.
由于某些原因我本科选了硕士课程,跳过了一些预备知识所以大家不要见怪。
PS:以上问题根据Minglei Xiao的答案做了纠正。
按投票排序按时间排序
9 个回答
如果用canonical quantization formulation的话,量子场论里场算符不一定是unitary演化了...场算符的演化按照
如何解释场算符的物理意义呢?依然是是概率诠释?量子场就是体系的基本自由度了,相当于广义坐标;从数学上讲,它是一个算符值分布。算符与波函数的关系相当于统计上的随机变量跟概率的关系。
 它首先是量子化的场论,我们可以按照场论来理解它,譬如,我们可以研究场关联函数:
它首先是量子化的场论,我们可以按照场论来理解它,譬如,我们可以研究场关联函数:
它又是量子力学算符。根据正则对易关系,在时刻
因此,存在一个表象

真空态
其中
自由场的谱密度是一个位于m处的狄拉克函数,其代表态表示一个自由粒子,叫做单粒子态。“正常”量子场论的谱密度类似于自由场(如图所示),它也包含一个单粒子态峰,它还可能包含若干个束缚态峰、多粒子态的连续统。非典型场论(强相互作用、具有奇怪对称性)的谱函数可能会更加复杂:例如 QED 由于规范对称性的保护,多粒子态连续统开始于电子质量,中间显然没有束缚态;QCD 更夸张,夸克的单粒子态根本就不存在。
 当然,场不仅能作用在真空态上,还可以作用在其他能量本征态上,如单粒子态
当然,场不仅能作用在真空态上,还可以作用在其他能量本征态上,如单粒子态这里,
学的时候一直没有给出波函数和field operator和波函数的具体形式,只是说存在这样的Hilbert space, 以及庞加莱群在这个空间上的representation.
除了自由场以外,我们很少见到波函数、场算符的具体形式。这主要是因为,它们一般没有解析形式。所有这些量中,最容易计算的是关联函数,方法就是费曼算术(Feynman's Calculus),又叫做“微扰论”。
量子态的Hilbert space 是否有具体的表象?
有啊 —— 当人们说某某希尔伯特空间的时候,就是指已经找到了一个具体的表象(包括一组基)。这些表象可以使用,例如,福克空间表示出来(暂时忘掉哈格定理)。 显示全部
Hilbert 空间从来都不是什么「波函数的空间」,而是量子态的空间。波函数只是态在一个表象下的形式。
微扰量子场论处理的是真空的微扰问题,涉及到的态都是渐进自由态,即进态、出态,它们都是动量本征态,对于不同自旋有不同的波函数,但总的来说都是自由粒子 。
。
你说的「场论里的波函数」是场算符吧,教授在第一节课就应该告诉你那个东西不是波函数。场算符的正则形式里,产生算符前那个系数才是对应的单粒子态的波函数。
——————————————————————
也不知道是不是学量子力学时净在解波函数的关系,有些人学场论的时候看不见「波函数」,心里总是没谱。
我们为什么要用量子场论?A.处理散射问题;B.处理物理参数的量子修正。至少在微扰论范围内,量子场论是干这些事的。这两个问题非相对论量子力学中处理不了,一是因为低能近似,二是粒子数守恒(薛定谔方程约化为概率流守恒),三是没有 off-shell propagator。
在低能非散射问题中,使用已修正的物理参数,非相对论量子力学完全够用,而且是足够精确的。而只有这类问题中适合使用波函数描述,因为能量较低使得很多粒子处于弱耦合但却相互束缚的状态:弱耦合意味着单粒子描述可用,顶多换个基研究 quasi-particle 那也是单粒子;束缚态表示有较稳恒的背景势,所以需要解定态波函数或者背景场中的近自由粒子,这些都不是真空中动量本征态,相对来说它们的波函数形式反而比相互作用更加 tricky。所以这些问题中人们比较关心波函数长什么样。
当然,有些这两个方法都不好用的情况,那就是强耦合体系。AdS/CFT 大法好!
微扰量子场论处理的是真空的微扰问题,涉及到的态都是渐进自由态,即进态、出态,它们都是动量本征态,对于不同自旋有不同的波函数,但总的来说都是自由粒子
你说的「场论里的波函数」是场算符吧,教授在第一节课就应该告诉你那个东西不是波函数。场算符的正则形式里,产生算符前那个系数才是对应的单粒子态的波函数。
——————————————————————
也不知道是不是学量子力学时净在解波函数的关系,有些人学场论的时候看不见「波函数」,心里总是没谱。
我们为什么要用量子场论?A.处理散射问题;B.处理物理参数的量子修正。至少在微扰论范围内,量子场论是干这些事的。这两个问题非相对论量子力学中处理不了,一是因为低能近似,二是粒子数守恒(薛定谔方程约化为概率流守恒),三是没有 off-shell propagator。
在低能非散射问题中,使用已修正的物理参数,非相对论量子力学完全够用,而且是足够精确的。而只有这类问题中适合使用波函数描述,因为能量较低使得很多粒子处于弱耦合但却相互束缚的状态:弱耦合意味着单粒子描述可用,顶多换个基研究 quasi-particle 那也是单粒子;束缚态表示有较稳恒的背景势,所以需要解定态波函数或者背景场中的近自由粒子,这些都不是真空中动量本征态,相对来说它们的波函数形式反而比相互作用更加 tricky。所以这些问题中人们比较关心波函数长什么样。
当然,有些这两个方法都不好用的情况,那就是强耦合体系。AdS/CFT 大法好!
看到邀请的时候别人已经回答过了...
Hilbert space是态的空间,不是波函数或场的空间。
概率解释在这里已经不适用了。之所以要有场论,正是因为人们研究相对论性的量子力学的时候,发现Klein-Gordon方程没有守恒的概率流(都没有守恒的概率流所以当然没法用概率解释来阐述其物理意义)、还存在负能解,而且同时,它不能用于描述有自旋的粒子。后来Dirac写出了Dirac方程,而这个体系虽然能描述有自旋的粒子,但它也存在负能解,为了解释这个负能解,Dirac说真空是一个Dirac海填满的,原先出于负能海的电子在吸收了能量后就被激发到具有正能的状态,相当于负能海里出现了一个空穴。然而作为一个描写一个粒子的方程,却实际描述的是多个粒子体系,显然已经不适用了。
所以人们抛弃概率解释,抛弃波函数,而用场的运动方程(Equation of Motion)来描述量子化的场。
然后场作为算符作用在粒子数表象下的态上,比如说作用在真空态|0>上就可以激发出粒子或反粒子。
Hilbert space是态的空间,不是波函数或场的空间。
概率解释在这里已经不适用了。之所以要有场论,正是因为人们研究相对论性的量子力学的时候,发现Klein-Gordon方程没有守恒的概率流(都没有守恒的概率流所以当然没法用概率解释来阐述其物理意义)、还存在负能解,而且同时,它不能用于描述有自旋的粒子。后来Dirac写出了Dirac方程,而这个体系虽然能描述有自旋的粒子,但它也存在负能解,为了解释这个负能解,Dirac说真空是一个Dirac海填满的,原先出于负能海的电子在吸收了能量后就被激发到具有正能的状态,相当于负能海里出现了一个空穴。然而作为一个描写一个粒子的方程,却实际描述的是多个粒子体系,显然已经不适用了。
所以人们抛弃概率解释,抛弃波函数,而用场的运动方程(Equation of Motion)来描述量子化的场。
然后场作为算符作用在粒子数表象下的态上,比如说作用在真空态|0>上就可以激发出粒子或反粒子。
1.
Q:如果用canonical quantization formulation的话
量子场论里场算符不一定是unitary演化了,如何解释场算符的物理意义呢?依然是是概率诠释?量子态的Hilbert space 是否有具体的表象?
A: 场算符是抽象的,所以需要Hilbert Space啊。场算符作用到Hilbert space中的态上面,给出了具有物理意义的场函数的值。
Hilbert space当然具有具体表象。和群论一样,谈的时候,是抽象的元素,用的时候,是某个具体的表象形式。
2
Q:学的时候一直没有给出波函数和field operator和波函数的具体形式,只是说存在这样的Hilbert space, 以及庞加莱群在这个空间上的representation.
A:后面就有了。不管谁讲,总会讲到real scalar, complex scalar, QED, ...
别着急,急可以先自己看看。
Q:如果用canonical quantization formulation的话
量子场论里场算符不一定是unitary演化了,如何解释场算符的物理意义呢?依然是是概率诠释?量子态的Hilbert space 是否有具体的表象?
A: 场算符是抽象的,所以需要Hilbert Space啊。场算符作用到Hilbert space中的态上面,给出了具有物理意义的场函数的值。
Hilbert space当然具有具体表象。和群论一样,谈的时候,是抽象的元素,用的时候,是某个具体的表象形式。
2
Q:学的时候一直没有给出波函数和field operator和波函数的具体形式,只是说存在这样的Hilbert space, 以及庞加莱群在这个空间上的representation.
A:后面就有了。不管谁讲,总会讲到real scalar, complex scalar, QED, ...
别着急,急可以先自己看看。
我决定来暴露身份答题——我的那帮一直想知道我知乎id的同学现在有机会了。。。我给他们讲过太多关于这些哭闹的小孩的故事了...
答主自己和很多人一样,也经历了无数挣扎才弄懂了量子力学和量子场论的结构,然后惊诧地发现,这东西一点也不玄乎,而且非常直观。
我们从一个简单的例子讲起。有一个小婴儿,他可能会哭闹也可能会平静,那么我们可以把他的状态标记成|A> 哭闹(A for angry)|C> 平静(C for calm)。如果我们不知道他现在究竟是哭闹还是平静,就需要用概率论来描述他的状态了。可以把他这时候的状态标记为Pa|A> + Pc|C>,也就是有Pa的概率他是Angry,有Pc的概率Calm,当然,如果只存在这两种状态,概率守恒告诉我们Pa + Pc = 1,这叫做基的完备性。如果你再研究出了点这个小孩的规律,比如这一秒他在哭,下一秒估计很大可能还是在哭,那么你就可以把这些研究成果写在一个矩阵(叫做transitional matrix)里面,每次乘在(Pa, Pc)这个向量上,然后,voilà,你就可以预知他的未来了。
那么现在问题弄得复杂一点,如果有两个小孩呢?这两个小孩可能有某种相互作用,比如一个听到另一个在哭,可能也跟着哭(当然也有可能是腹黑小萝莉,听到旁边的小正太哭了就开始大笑),那么他们的联合态空间就是|AA>, |AC>, |CA>, |CC>,其中每个代表这两个小孩,比如|AC>代表第一个小孩Angry,第二个小孩Calm,其他类推。把这几个状态的概率算清楚,就完整地描述了此刻的状态;这两个小孩的随着时间的变化也可以写到一个transitional matrix里面,显然,这个矩阵是4乘4的。恭喜你,你已经能预测两个小孩的未来了。
然后呢,任意多个小孩的故事也就自然地能理解了。注意这时候地联合态空间可能比较大,|AAAAAAAAA>, |AAAAAAAAC>, |AAAAAAACA>, |AAAAAAACC>, ...很多的态构成了这个态空间,而相应的概率就是态向量,转换矩阵就是这个空间上的算符。
所以这个就是希尔伯特空间了?还不是,量子力学的故事比这个稍微再麻烦一点。如果这些孩子是量子的(我也不知道应该怎么做,用球状闪电照一下?),那么他们处于某个态的概率不是态向量里面的系数P,而是它的模方|P|^2 = P*P.conjugate(). 这个基本没有影响我们的分析,唯一的不同在于P可以是复数了,从而概率归一条件从所有系数加起来等于1变成了所有系数的模方加起来等于1——这些向量组成的空间就是一个希尔伯特空间了,我们把同一个方向不同长度的向量当作同一个,就是所谓模方等于1的归一化条件。至于上面说的转换矩阵,也换成了量子力学里面的时间演化算符e^{iHt}. 除此之外,一切还是那些小孩哭闹的故事。
如果我们进一步推广,这些小朋友可以不仅仅有平静和哭闹两个状态,而是可以在一个房间里面到处爬,那么他们的状态就需要描述成|x>也就是坐标。比如|门边>, |桌子上>, |马桶盖上>,这时候一个小孩从门边爬到桌子上就可以等价地看成把门边这个小孩杀掉,然后在桌子上产生一个小孩。做这些操作的数学工具就是场算符(分成产生和消灭算符两类,而且还跟位置有关)。这里面的细节如对易子还有小孩的全同性就跳过去了,理解概念框架本身更重要。
接下来回答什么是波函数:波函数就是这个态的系数!比如 |孩子的状态> = a|门边> + b|桌子上> +c|马桶上>,那么波函数就是 \psi(x): if x = 门边 then \psi = a; if x = 桌子上 then \psi = b; if x = 马桶上 then \psi = c. 如果你的空间弄成连续的三维空间,我的\psi就成了关于三维空间的函数,也就是量子力学课上学的那个“波函数”。自然地,你关心的信息不同,得到的波函数就不同,所以嘛,态本身是本质的,波函数是拿来刻画态的。
最后一个问题,non-unitary field evolution. 还记得我们刚才说的经典哭闹小孩的故事么?我们用一个transitional matrix去演化小孩的状态,那么这个小孩的态向量就从(Pa, Pc)变成了(Pa', Pc')。非常重要的一点是,如果就这两个状态,Pa+Pc = 1, Pa' + Pc'也得是1。(否则这个小孩就有一定的概率直接消失了!)这就对transitional matrix提出了相应的要求。量子的故事也是一样的,只是改成了|Pa|^2 + |Pc|^2 = 1, |Pa'|^2 + |Pc'|^2 = 1——这个要求满足的条件就是e^{iHt}是unitary的,或者说H是Hermitian的。如果某个理论里时间演化算符e^{iHt}不是unitary的,小孩子就是会无端失踪。。。这样的理论还是有应用的,比如说你去考虑冷原子里面抓获了一个原子,它就有一定的概率会跑掉啊,所以描述它的理论就可以是non-unitary的;或者高能里面的例子,粒子会衰变的...——高能我就不熟了,自行看书自求多福吧。 显示全部
答主自己和很多人一样,也经历了无数挣扎才弄懂了量子力学和量子场论的结构,然后惊诧地发现,这东西一点也不玄乎,而且非常直观。
我们从一个简单的例子讲起。有一个小婴儿,他可能会哭闹也可能会平静,那么我们可以把他的状态标记成|A> 哭闹(A for angry)|C> 平静(C for calm)。如果我们不知道他现在究竟是哭闹还是平静,就需要用概率论来描述他的状态了。可以把他这时候的状态标记为Pa|A> + Pc|C>,也就是有Pa的概率他是Angry,有Pc的概率Calm,当然,如果只存在这两种状态,概率守恒告诉我们Pa + Pc = 1,这叫做基的完备性。如果你再研究出了点这个小孩的规律,比如这一秒他在哭,下一秒估计很大可能还是在哭,那么你就可以把这些研究成果写在一个矩阵(叫做transitional matrix)里面,每次乘在(Pa, Pc)这个向量上,然后,voilà,你就可以预知他的未来了。
那么现在问题弄得复杂一点,如果有两个小孩呢?这两个小孩可能有某种相互作用,比如一个听到另一个在哭,可能也跟着哭(当然也有可能是腹黑小萝莉,听到旁边的小正太哭了就开始大笑),那么他们的联合态空间就是|AA>, |AC>, |CA>, |CC>,其中每个代表这两个小孩,比如|AC>代表第一个小孩Angry,第二个小孩Calm,其他类推。把这几个状态的概率算清楚,就完整地描述了此刻的状态;这两个小孩的随着时间的变化也可以写到一个transitional matrix里面,显然,这个矩阵是4乘4的。恭喜你,你已经能预测两个小孩的未来了。
然后呢,任意多个小孩的故事也就自然地能理解了。注意这时候地联合态空间可能比较大,|AAAAAAAAA>, |AAAAAAAAC>, |AAAAAAACA>, |AAAAAAACC>, ...很多的态构成了这个态空间,而相应的概率就是态向量,转换矩阵就是这个空间上的算符。
所以这个就是希尔伯特空间了?还不是,量子力学的故事比这个稍微再麻烦一点。如果这些孩子是量子的(我也不知道应该怎么做,用球状闪电照一下?),那么他们处于某个态的概率不是态向量里面的系数P,而是它的模方|P|^2 = P*P.conjugate(). 这个基本没有影响我们的分析,唯一的不同在于P可以是复数了,从而概率归一条件从所有系数加起来等于1变成了所有系数的模方加起来等于1——这些向量组成的空间就是一个希尔伯特空间了,我们把同一个方向不同长度的向量当作同一个,就是所谓模方等于1的归一化条件。至于上面说的转换矩阵,也换成了量子力学里面的时间演化算符e^{iHt}. 除此之外,一切还是那些小孩哭闹的故事。
如果我们进一步推广,这些小朋友可以不仅仅有平静和哭闹两个状态,而是可以在一个房间里面到处爬,那么他们的状态就需要描述成|x>也就是坐标。比如|门边>, |桌子上>, |马桶盖上>,这时候一个小孩从门边爬到桌子上就可以等价地看成把门边这个小孩杀掉,然后在桌子上产生一个小孩。做这些操作的数学工具就是场算符(分成产生和消灭算符两类,而且还跟位置有关)。这里面的细节如对易子还有小孩的全同性就跳过去了,理解概念框架本身更重要。
接下来回答什么是波函数:波函数就是这个态的系数!比如 |孩子的状态> = a|门边> + b|桌子上> +c|马桶上>,那么波函数就是 \psi(x): if x = 门边 then \psi = a; if x = 桌子上 then \psi = b; if x = 马桶上 then \psi = c. 如果你的空间弄成连续的三维空间,我的\psi就成了关于三维空间的函数,也就是量子力学课上学的那个“波函数”。自然地,你关心的信息不同,得到的波函数就不同,所以嘛,态本身是本质的,波函数是拿来刻画态的。
最后一个问题,non-unitary field evolution. 还记得我们刚才说的经典哭闹小孩的故事么?我们用一个transitional matrix去演化小孩的状态,那么这个小孩的态向量就从(Pa, Pc)变成了(Pa', Pc')。非常重要的一点是,如果就这两个状态,Pa+Pc = 1, Pa' + Pc'也得是1。(否则这个小孩就有一定的概率直接消失了!)这就对transitional matrix提出了相应的要求。量子的故事也是一样的,只是改成了|Pa|^2 + |Pc|^2 = 1, |Pa'|^2 + |Pc'|^2 = 1——这个要求满足的条件就是e^{iHt}是unitary的,或者说H是Hermitian的。如果某个理论里时间演化算符e^{iHt}不是unitary的,小孩子就是会无端失踪。。。这样的理论还是有应用的,比如说你去考虑冷原子里面抓获了一个原子,它就有一定的概率会跑掉啊,所以描述它的理论就可以是non-unitary的;或者高能里面的例子,粒子会衰变的...——高能我就不熟了,自行看书自求多福吧。 显示全部



No comments:
Post a Comment