 是超出水面的高度;对於声波,
是超出水面的高度;对於声波, 是超气压
是超气压http://zh.wikipedia.org/wiki/%E6%B3%A2%E7%9F%A2
波矢有两种常见的定义,区别在於振幅因子是否乘以
 ,两种定义分别用於物理学和晶体学以及它们的相关领域。[1]
,两种定义分别用於物理学和晶体学以及它们的相关领域。[1][编辑] 物理学定义
理想的一维行波遵循如下方程:- x为位置;
- t为时间;
 (x和t的函数)是对波进行描述的扰动(例如对於海浪,
(x和t的函数)是对波进行描述的扰动(例如对於海浪, 是超出水面的高度;对於声波,
是超出水面的高度;对於声波, 是超气压);
是超气压);- A是波的振幅(振动的峰值);
 是相位偏移,描述了两个波互相之间不同步的程度;
是相位偏移,描述了两个波互相之间不同步的程度; 是波的角频率,描述了在一个给定点波振动的快慢程度;
是波的角频率,描述了在一个给定点波振动的快慢程度; 是波数,与波长成反比,由
是波数,与波长成反比,由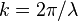 求出。
求出。
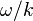 。
。推广到三维情况下,方称为:
- r是三维空间中的位置矢量;
 是矢量点积;
是矢量点积;- k是波矢。
 。波矢的方向是平面波行进的方向
。波矢的方向是平面波行进的方向


No comments:
Post a Comment