| |
今天我們所要討論的是一個跟數學與物理有關的題目,而這個題目如果從歷史上來看的話,它是來自於物理的,當然現在是屬於數學的範疇,我們現在就看一看。
第一個公式叫做Stokes'定理, 我們把它寫下來是這樣的一個公式:
上面這個公式, 一邊是線積分, 一邊是面積分, 所以我要假設各位已經有了線積分和面積分的基礎, 那麼這個公式是什麼意思呢?
就是說我們假設空間中有一個向量 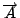 (如圖1) , (如圖1) , 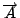 是隨著空間的點在變, 不同的點上有一個不同的向量, 這樣的東西我們就叫做一個向量場。
然後,我們隨便畫一個曲線 C,那麼我們就可以把這個向量場沿著這個曲線去做線積分,積完以後我們就得到一個值,這個值是等於什麼東西呢?
假如在這個曲線上,我們拿出一塊布把它蓋起來。造一個曲面,而以這個曲線為邊界。我們現在就利用剛剛那個向量場來求一個叫做旋度(curl)的東西,它的公式是 是隨著空間的點在變, 不同的點上有一個不同的向量, 這樣的東西我們就叫做一個向量場。
然後,我們隨便畫一個曲線 C,那麼我們就可以把這個向量場沿著這個曲線去做線積分,積完以後我們就得到一個值,這個值是等於什麼東西呢?
假如在這個曲線上,我們拿出一塊布把它蓋起來。造一個曲面,而以這個曲線為邊界。我們現在就利用剛剛那個向量場來求一個叫做旋度(curl)的東西,它的公式是
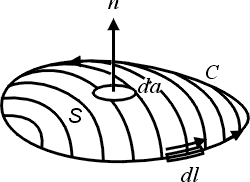
圖1 |
curl 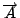 是由 是由 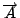 導出的另一個向量場。其中 導出的另一個向量場。其中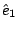 是指x軸, 是指x軸, 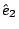 是y軸, 是y軸, 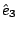 是z軸, 是z軸, 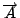 在x、 y、 z軸上的三個分量,
我們分別表示為A1、A2、A3, 它們都是函數, 因為 在x、 y、 z軸上的三個分量,
我們分別表示為A1、A2、A3, 它們都是函數, 因為 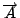 是隨著 x、y、z 在變, 所以 A1、A2、 A3當然也是函數。這裡我們為了等一下的理由把x、 y、z 改寫成x1、x2、x3, 然後把 是隨著 x、y、z 在變, 所以 A1、A2、 A3當然也是函數。這裡我們為了等一下的理由把x、 y、z 改寫成x1、x2、x3, 然後把 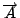 的分量A1、A2、A3 對x1、x2、x3 分別取導數, 再經過適當的運算,我們就得到一個由 的分量A1、A2、A3 對x1、x2、x3 分別取導數, 再經過適當的運算,我們就得到一個由 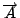 所導出的向量場, 當然, 在每一個地方都有一個curl 所導出的向量場, 當然, 在每一個地方都有一個curl 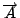 , 我們把每一點的curl , 我們把每一點的curl 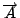 這個向量跟剛剛我們造的這個曲面當點上的法向量
這個向量跟剛剛我們造的這個曲面當點上的法向量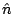 去做內乘(dot), 做完以後這也是一個函數, 在曲面上每一點都有一個值,
然後乘上曲面的面積元素da去做曲面積分, 所得到的結果和剛才的線積分相等,
這就是Stokes'定理。我們要注意一件事情, 這個曲面是任意的, 可以證明, 對於任意一個以這個曲線為邊界的曲面, 我們所做出來的積分值不變, 換句話說,
我們到底選擇什麼曲面並沒有關係。
底下我們再介紹另外一個定理, 我們叫做Gauss定理 去做內乘(dot), 做完以後這也是一個函數, 在曲面上每一點都有一個值,
然後乘上曲面的面積元素da去做曲面積分, 所得到的結果和剛才的線積分相等,
這就是Stokes'定理。我們要注意一件事情, 這個曲面是任意的, 可以證明, 對於任意一個以這個曲線為邊界的曲面, 我們所做出來的積分值不變, 換句話說,
我們到底選擇什麼曲面並沒有關係。
底下我們再介紹另外一個定理, 我們叫做Gauss定理
我們還是一樣在空間中有一個向量場 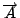 , 然後我們現在選一個封閉的曲面S,
一個封閉的曲面就會包圍一個體積V(如圖2) , 然後我們現在選一個封閉的曲面S,
一個封閉的曲面就會包圍一個體積V(如圖2)
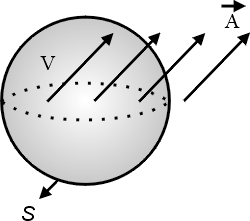
圖2 |
然後我們跟剛剛一樣在曲面上做曲面積分, 剛剛是用curl 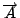 去做, 現在我們用 去做, 現在我們用 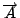 本身去做, 這個意義是完全一樣, 我這裡特別在積分符號上畫個圈, 只不過強調現在的S是一個封閉的曲面。我們現在看右邊, 右邊是利用
本身去做, 這個意義是完全一樣, 我這裡特別在積分符號上畫個圈, 只不過強調現在的S是一個封閉的曲面。我們現在看右邊, 右邊是利用 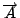 去做一個跟它相關的東西, 我們叫做散度(divergence), 用 去做一個跟它相關的東西, 我們叫做散度(divergence), 用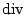 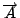 = =
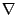 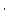 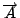 來表示, 剛剛我介紹的curl 來表示, 剛剛我介紹的curl 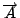 是一個向量, 現在所介紹的 是一個向量, 現在所介紹的 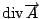 本身並不是一個向量, 而是一個數量函數, 它的定義是 本身並不是一個向量, 而是一個數量函數, 它的定義是
這個函數在V裡面每一點都有一個值, 然後乘上d3x這個小體積去做體積分,
結果我們得到邊界上的曲面積分等於裡面的體積分, 這就是Gauss定理。
Stokes' 定理與Gauss定理會成立的原因, 其實就是微積分基本定理(Fundamental Theorem of Calculus),
微積分基本定理是這樣的一個公式:
右邊是1-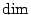 的積分, 左邊是0- 的積分, 左邊是0-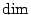 , 如果我們有一個線段, 它有兩個邊界a和b, 那麼點算是0- , 如果我們有一個線段, 它有兩個邊界a和b, 那麼點算是0-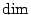 的東西, 所以左邊算是0- 的東西, 所以左邊算是0-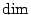 的一個量, 微積分基本定理就是函數在這兩個點上的值的差f(b)-f(a) 等於在這個線段上的這個函數導數的積分,
當然這個定理各位都很熟悉, 而事實上這個定理也是在所有數學中最重要的一個定理。這個定理我們有各種各樣的變形,
可以將它推廣到高維空間上面。現在我們看Stokes' 定理, 左邊是1- 的一個量, 微積分基本定理就是函數在這兩個點上的值的差f(b)-f(a) 等於在這個線段上的這個函數導數的積分,
當然這個定理各位都很熟悉, 而事實上這個定理也是在所有數學中最重要的一個定理。這個定理我們有各種各樣的變形,
可以將它推廣到高維空間上面。現在我們看Stokes' 定理, 左邊是1-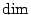 , 因為它是線積分, 在線上面做1- , 因為它是線積分, 在線上面做1-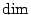 的積分, 等於一個2- 的積分, 等於一個2-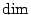 的積分, 而這個1- 的積分, 而這個1-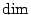 的積分區域是2- 的積分區域是2-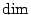 積分區域的邊界, 我們剛才所定義的curl 積分區域的邊界, 我們剛才所定義的curl 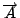 是 是 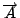 的一種導數, 所以右邊就變成一個函數導數的積分; Gauss定理也是同樣的道理, 所以這兩個定理只不過是微積分基本定理應用到1-
的一種導數, 所以右邊就變成一個函數導數的積分; Gauss定理也是同樣的道理, 所以這兩個定理只不過是微積分基本定理應用到1-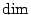 和2- 和2-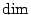 的關係、2- 的關係、2-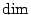 和3- 和3-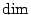 的關係而已。其實這樣的定理有很自然的推廣,可以推廣到(n-1)- 的關係而已。其實這樣的定理有很自然的推廣,可以推廣到(n-1)-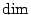 和n- 和n-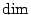 的關係, 當然我們必須要知道如何把curl和divergence的觀念推廣到n維的情況, 推廣出去之後的定理通稱為Stokes' 定理。 的關係, 當然我們必須要知道如何把curl和divergence的觀念推廣到n維的情況, 推廣出去之後的定理通稱為Stokes' 定理。
|
|
對外搜尋關鍵字:
.Stokes'定理
.電磁學
.Gauss定理
.curl
.微積分基本定理
.Gauss
.Diracδ 函數
.Maxwell
.wave
equation |
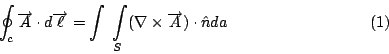
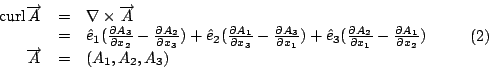
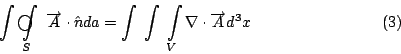


No comments:
Post a Comment