4.4 Higher Dimensions

Behind all of this geometry we've been talking about is a mathematical concept which describes such spaces as the Mobius strip and the three dimensional prism with triangles for faces. The term mathematicians use to describe these spaces is orbifold.
To define an orbifold, think of what we've been doing when we construct these chord spaces. Think of the two dimensional case. We saw that we have a surface containing all the two chords of two pitch classes. And we also saw that there are points on this surface that allow you to circle back to the other side. To construct our space, we folded, twisted, and glued those points together which allowed you to circle back to the otherside. This created our chord space and is in fact the way an orbifold is created. Given a symmetric surface (our chords) and then by taking all the points which look alike we fold and twist until the identical points have been brough together (glued) [6].
The origin of the term orbifold (orbit-manifold) is due to William Thurston [5] and is a special kind of manifold. We will not get into manifolds here, but it is worth mentioning that the orifold is a kind of manifold.
The notion used for this is as follows.

Symbol	Meaning
`Tⁿ`	This refers to a torus in `n` dimensions. You can think of a torus as a donut, or to be more specific, a torus is the product of two circles [20].
`S_n`	This refers to the symmetric group in `n` dimensions, where we have the set of permutations on the objects in `S`
`Rⁿ`	The set of all real numbers, in `n` dimensions.
`12Zⁿ`	The set of all positive and negative multiples of 12 in `n` dimensions.
`Rⁿ/12Zⁿ`	Here we have a set of sets. Each element in `Rⁿ/12Zⁿ` is a set of integers. To see this, consider the case when `n=1`. Here we have `R12Z = { {0,12,24,36,...}, {1,13,25,37,...}, ..., {11,23,35,47,...} }`. You can think of these as our pitch classes.

Using the notation above, we can define an n-torus Tⁿ to be Rⁿ/12Zⁿ. And we can then define our orbifold to be Tⁿ/S_n. This works out to [Rⁿ/12Zⁿ]/S_n, which is really Rⁿ/[12Zⁿ⋊S_n]. Now, we need a special way to take the product between the groups 12Zⁿ and S_n. We can define the product to be the semi-direct product. Without getting too much into group theory, this means that there is a group which can be formed by taking the semi-direct product between 12Zⁿ and S_n [2, p.7]. This group retains certain properties [22].
The group Rⁿ/[12Zⁿ⋊S_n] is our orbifold. These orbifolds can be constructed by describing what is called a fundamental domain of 12Zⁿ⋊S_n in Rⁿ. What this means is that a smaller pattern can be used to describe a larger pattern [21].
This is useful since it can be used to describe the the mobius strip in the two dimensional case and the prism with triangular faces in the three dimensional case, and also describe geometric spaces up to dimension n. Consider of all the points in Rⁿ, only the ones where the coordinates are sorted in nondecreasing order. Let them be of the form (x₁,...x_n). Now we further restrict these points so that x_n ≤ x₁ + 12 and that the sum of all the x_i is greater than or equal to zero and less than or equal to twelve. By gathering all these points we will form an n dimensional prism with the base being a figure in n-1 dimensions, in this case a line. Consider the prism in two dimensions below with a line for the base (highlighted in red).

Figure 4.4.1: 2D prism from the fundamental domain construction.

From the above we see something interesting. Recall that since we are working in a group modded by 12Z any negative number -x is really 12-x. This is exactly like going counter clock-wise on our pitch-class circle. We just start at zero on the circle and step counter-clockwise x times. So, in our space we see that the point (-6,6) is really the same as (6,6). Starting to seem familiar? It should remind you of the following figure.

Figure 4.4.2: 2D chord space

If you tilt your head a little then this is what we saw earlier in the two dimensional case of chord geometries. So, we see that algebraically we can describe this space. And Dmitri Tymoczko gives a function for the twisting of the surface to match up points with thier counter-parts [2, p.7].

O(x₁,...,x_n) = (x₂-12/n, ...,x_n-12/n, x₁+12-12/n)

By using this function on all the points in our prism, we can find all the chords related by transposition and with the pitch classes summing to the same value. In the orbifold, this function is a rotation when the prism has odd dimension and a rotation and reflection otherwise [2, p.7].
One last note about the orbifolds. Those chords which lie at the center of the orbifold (that divide the octave evenly) are known as T-symmetrical chords. This is because by transposition, they are all related. Also we can define the chords which lie along the boundary, furthest from dividing the octave evenly. These are called P-symmetrical since up to permutation they are the same. For example CCC is a P-symmetrical chords. Lastly, we can define those chords which are inversionally symmetrical to be I-symmetrical chords [1, p.74].

不一样的贪吃蛇

陳浩 · 6 个月前

这个专栏文章由问题「莫比乌斯带上的棋盘？」引发。其中内容我很确定在某个答案里写过，不过找不着了。莫比乌斯带，克莱因瓶等，看着非常高大上，其实把正方形的四边做合适的粘连就可以得到了。下面五个图来自维基百科的相关页面，每个图上我都大致画了「一条」带方向的线段（黑色细线，可能不是很直）。你看的出这些分别是什么曲面吗？
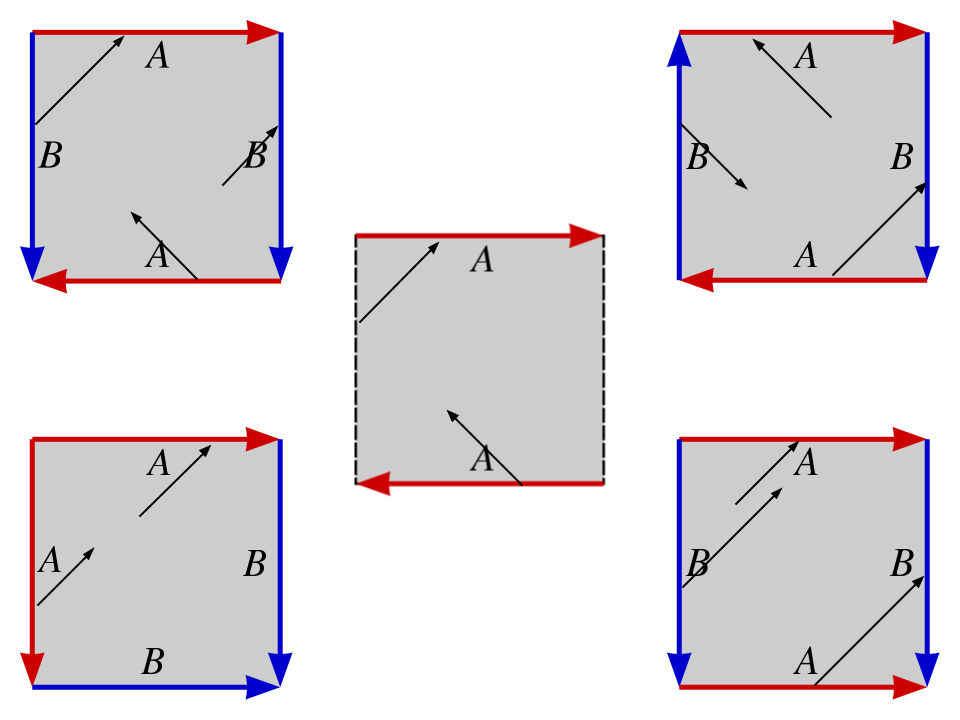图中正方形的边界都用红色或蓝色的箭头标注，表示同色的边界按标注的方向粘合。
先看右下角的图
设正方形左下角坐标 (0,0)，右上角坐标 (1,1)。因为上下边界被粘合起来，坐标为 (x,1) 的点被等同于坐标为 (x,0) 的点。同样的，左右边界被粘合起来，所以坐标 (0,x) 的点被等同于坐标为 (1,x) 的点。
试想我所画的黑线是一个正在走直线的贪吃蛇的路径。它向右上方行进，先碰到了上边界，于是从下边界同样的横坐标处出现，继续向右上方行进，碰到右边界，然后从左边界同样的高度出现，继续向右上行进。这是大家非常熟悉的情景，有些地方叫作「周期性边界条件」。
这是什么曲面呢？很容易想象……把正方形卷成一个筒，然后再把两端接起来……没错这是一个 torus（轮胎面？甜甜圈面？）
再看左下角的图
根据标注的箭头， (0,x) 被等同于 (1-x,1)，(x,0) 被等同于 (1,1-x)。这是什么曲面呢？球面。也许换个角度就更加明显了：是想一个地球，左上角是北极，右下角是南极，而 (0,0)-(1,1) 这条对角线是赤道。而左边和下面的边界，分别等同于上面和右边的边界，是「国际日期变更线」。
再看中间那幅图
根据标注的箭头，左右边界没有粘合。而上下边界，注意粘合的方向：(x,0) 被等同于 (1-x,1)。我所画的贪吃蛇，先是向右上方向行进，在偏左的地方碰到了上边界。于是他从下边界偏右的地方出现，向左上方向行进。这是什么曲面呢？注意粘合的方向是反的，是「扭」了一下再粘起来的。这正是莫比乌斯带。
现在你们知道怎么玩了，其实就是玩贪吃蛇的时候加上个变态的边界条件而已。上方的两幅图我就直接公布答案了：他们分别是克莱因瓶和射影平面。如果有人设计出这样的贪吃蛇，不知会不会流行。很有挑战不是吗？
对于数学基础不错的同学们来说，这也许太简单了。我就再贴两个当年初学时颇耗了我一些脑细胞的曲面。第一个是二维的 Dunce hat (topology)：

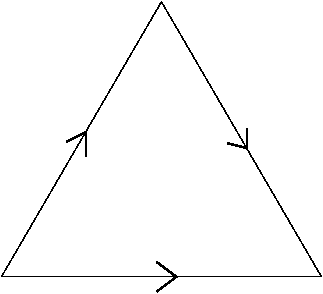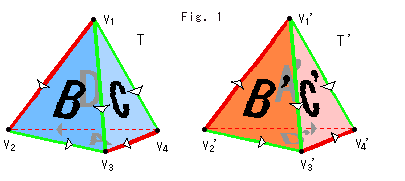
这三条边要全部按给定的方向粘合起来，三个点也因此相互等同。因此最后的结构中只有一个点，一条边，一个面。其实粘合左边和下边还是比较容易想象的，结果是一个圆锥。然后右边要怎么处理呢？想要直观可以看这个视频 https://www.youtube.com/watch?v=34j4CppfRTA 他在一块布上缝了两个拉链，做出了这个曲面。结果是一个很萌很萌的睡帽。
第二个是粘合两个四面体得到的三维流形，图片来自：Figure-8 Knot (2)