Monday, July 15, 2013

gauss01 Gauss在1827年的文章中，对于一个由测地线构成的三角形，证明了一条关于曲率的著名定理。设K是一个曲面的可变曲率，于是∫∫KdA是这个曲率在面积A上的积分；Gauss的定理用于这三角形时说∫∫KdA等于三个角之和减去π；这就是说，在一个测地三角形上曲率的积分等于三个角之和超过180度的盈量，或在三个角之和小于180度量，等于三个角之和不足180度的亏量；Gauss说这个定理应该算是一个最精美的定理；这个结果推广了Lambert的定理，后者断言球面三角形的面积等于它的球面盈量与半径平方之积，因为在一个球面三角形上K是常数且等于半径平方的倒数

Gauss在1827年的文章中，对于一个由测地线构成的三角形，证明了一条关于曲率的著名定理。设K是一个曲面的可变曲率，于是∫∫KdA是这个曲率在面积A上的积分；Gauss的定理用于这三角形时说∫∫KdA等于三个角之和减去π；这就是说，在一个测地三角形上曲率的积分等于三个角之和超过180度的盈量，或在三个角之和小于180度量，等于三个角之和不足180度的亏量；Gauss说这个定理应该算是一个最精美的定理；这个结果推广了Lambert的定理，后者断言球面三角形的面积等于它的球面盈量与半径平方之积，因为在一个球面三角形上K是常数且等于半径平方的倒数

分享日志
热门日志
细胞量子场论…………无语了…………

细胞量子场论…………无语了…………

来源：陈文珩的日志

量子细胞场论是统一场论的关键

量子细胞场论是唯一与现有的粒子物理标准模型和广义相对论两者都最大兼容的(Maximal Compatible)模型。所谓最大兼容是指在可观测效应上两者完全兼容，在不可观测效应上两者略有差异。量子细胞场论的出发点有两个：一是射影丛，二是细胞量子化。

由几何的观点我们知道，洛仑兹群(Lorentz Group)是一个酉模仿射群，因此我们应当从射影群出发定义协变性，由于还没有人仔细研究这个群，我们不妨称之为爱因斯坦群。所以要与狭义相对论相容，引入射影空间是必然的，我们称之为爱因斯坦空间，这是一个完备的空间，是由酉模仿射空间加上它的射影补丁构成的。要与规范场论兼容，则引入射影丛也是必然的，也就是说，射影变换不是全局的，而是在空间中的每一点定义的。这里没有欧氏空间中的绝对原点，只有相对原点。

所谓细胞量子化，是推测粒子是一种自对偶的细胞。普通的细胞具有粒子性也具有不确定性，不确定性是由于食物分布的不确定性引起的，所以细胞既有粒子的特点也有场的特点，但这种场具有与背景相关的特点。因此我们说粒子是一种自对偶的细胞，想象粒子有一个与之伴随的对偶细胞是在空间中随机分布的，但这种分布只与粒子本身有关。这样我们就摈弃了以太说，也不再需要Dirac海，不需要虚空间中充满了检测不到的希格斯粒子。规范场是相位因子场，而相位因子与量子细胞周期是等价的概念。

量子细胞场论的最大特点是一切推导过程都是自然的，规范场论通过引入规范变换增加了场的自由度，然后通过指定规范再限制自由度，但这种增加与限制自由度的方法都是人为引入的。量子细胞场论则不同，射影空间有最大的自由度，物理空间有最小的自由度，但众所周知，洛仑兹群是非紧致(Non-compact)群，当我们要求物理空间必须是紧致的(Compact)。从Klein的变换群等级可以知道，射影群引出的联络必须约化成U(1)、SU(2)和SU(3)群，也就是标准模型中定义联络的几个群。

另一方面，由Klein的变换群观点可知，物理空间中爱因斯坦群必须约化成保持幺正性的旋转群，这就很自然地引出了自旋。平移变换只能作为一种导出的结果，传统方法也可以导出类似的结论；比如你可以从共形群(Conformal)出发导出自旋，也是一种先增加很多自由度，再限制自由度的方法，相比之下，会使问题复杂化。

由非对易几何出发，可以导出中间矢量玻色子的质量是一种电弱“磁”效应，同样由量子细胞场论出发，也可以导出类似的结果。平移变换只能是一种导出结果，由射影群到酉模仿射群，能够保持相对原点不变的变换只可能有两种，一种就是传统意义上的“电荷”，另外一种就是“质心荷”，这是标准模型中没有考虑的情况。射影空间中有点与线的对偶性，投射到物理空间，可以自然地引出玻色子的纵向极化分量。所以说，量子细胞场论是一种最简单的同时满足可重正化要求又能引入玻色子质量的模型。

量子引力理论一直困难重重。使用正则量子化方法的圈量子引力是一种背景无关的理论；超引力遭遇到不可重正性的难题；广义相对论是背景无关的，弦论虽可解决重正化难题，却是一种背景相关的理论，发展下去也必须引入以太、Dirac海和希格斯(Higgs)粒子等类似的概念，例如超弦允许有多达数万种的真空状态。引力子的自旋为2，要想将引力量子化，超对称性是必需的，在超引力和弦论中，超对称性又是人为引入的，就导出了没有实验依据的超伙伴粒子，并且这样的理论也是丑陋的，很难想象造物主会用这么丑陋的方式创造世界。细胞量子化方式却是自然地引入了超对称性。
递归

弦论无法解决粒子的手征性问题，只有引入超对称性和高维空间后，超弦才能解决手征性问题。手征性在量子细胞场论里不是问题，我们假定电子中微子是零阶细胞，而电子为一阶细胞就可以了，现实世界中零阶细胞包括病毒等，一阶细胞包含细菌等，这在形式逻辑中有一个对应物，就是一阶谓词逻辑，就是哥德尔(Godel)发现不完备定理的那个逻辑。

同一阶谓词逻辑不一样的地方，这里我们引入了一个一阶递归(First-Order Recursive)算符，一阶算符在很多量子场论里都是必须的，比如非对易几何，再比如Dirac场(可以参见Greiner写的《量子力学导论》)，但递归算符却是可重正化理论要求的。

重正化与标度不变性有关，当我们实施一个标度变换，相应的场不会因为标度变换而发生改变，我们才说这个场论是可重正的。所以量子场论里的信使粒子必须是无质量的，质量的存在会破坏标度不变性。量子细胞场论里可以运用动态重正化技术，相信这种动态重正化技术对于强相互作用以及量子引力是必要的技术，为了有所区别我们将传统量子场论中的重正化技术称为静态重正化技术。酉模仿射变换可以保持两类相对原点不变，即电荷不变性与质心荷的不变性，当我们要求一阶条件时，很自然粒子的电荷与质心荷必须重合，这就引出了Dirac场，由于Dirac场、Gordan场与传统的Schodinger场都是色散场，动态重正化技术保证了电荷与质心荷在色散场中也保持重合。所以可以认为递归条件是量子细胞场论里的Ward恒等式。

为了看清量子细胞场论与量子场论的关系，我们引入线性逻辑中的复制算符“!”和对偶“?”，我们知道它们等价于量子场论中的产生和湮灭算符。公理化量子场论的基础是直觉逻辑，通过复制算符和对偶算符可以将直觉逻辑嵌入到线性逻辑中，从而量子细胞场论与量子场论是严格等价的；但有一个重要的区别，线性逻辑尊重资源有限的事实，这就给二次量子化加了一个限制，所以原则上量子细胞场论可以是一门抛弃了无穷大的学问；量子场论中虚粒子可以被任意的复制正是无穷大产生的根源。

自旋是量子场论中最基本的概念，可以说不了解自旋就不可能明白量子场论；但自旋没有经典物理的对应物，想像如果电子像地球一样自转的话，电子的表面将不得不以光速的两倍旋转，这显然是不可能的；量子场论中只能以较抽象的方式讨论自旋，估计盯着Dirac方程看上半天也未必能明白自旋是怎么回事。实际上，自旋在细胞的世界里是有对应物的，就是细胞周期，还有就是人体内的能量ATP循环，ATP循环只是一种逻辑上的旋转，只有当你说话或者走路的时候才会转化成真实的物理波动。对于量子细胞而言，自旋、递归和量子细胞分裂是严格等价的，这是狭义相对论所要求的；狭义相对论是一种超等的理论，洛伦兹对称性是严格成立的；但生物中的细胞分裂能够实现的是一种伪递归，用普里高津的话说，生物是一种耗散结构，对称性被破坏了。
字典

动态重正化技术自然地保证了费米子的自旋是1/2，动态重正化可以看成是自对偶细胞的细胞分裂过程，现在世界中，细菌通过细胞分裂自我繁殖。为了看清射影几何与量子细胞场论之间的关系，我们需要射影丛几何与量子场论对应关系的一个字典。

将复射影空间投射到仿射空间中，酉模仿射变换可以保持一个无穷远直线不变，并且可以保持两个虚园点不变，这样我们就建立了与量子场论对应关系的一个字典。

复射影空间中的概念	量子场论中的概念
虚园点(Circular Point)	正电荷或负电荷
无穷远直线	光子的世界线
酉模仿射变换	洛伦兹变换
仿射补丁	荷
点线对称性	电流连续性方程
二级退化曲线	核力同位旋场,Higgs复标量场
二级退化曲线X+iY	带正电荷的W玻色子场
二级退化曲线X-iY	带负电荷的W玻色子场
水平正交标架	爱因斯坦-玻色统计
垂直正交标架	费米-狄拉克统计

细胞量子化是一种与路径积分量子化方法大体上兼容的量子化方法，但细胞量子化更侧重于数学上所谓的微局部分析，我们更关心一个自对偶细胞周期内发生的事情；由于有质量粒子与无质量粒子明显存在于一个双曲空间中，加上逆归条件和动态重正化方法，自然可以得出费米子波函数的反对称统计性质；细胞量子化方法还有一个好处是可以用统一的几何语言处理对称统计和重正化问题。对费米子场而言，对偶性与手征性是等价的。以光子为例，电场与磁场相互转化，但光子的总能量是固定不变的；所以，量子细胞有零点能，一对相互对偶的场互相转化，将场进行傅里叶变换就得到对偶场，零点能就相当于自对偶的帕斯瓦尔定理。

由于荷与无穷远直线有两个交点，因此对应的是双曲几何，引出的力是排斥性的。玻色子满足谐和坐标条件，相应的微分算子是椭圆的，与无穷远直线没有交点，引出的力是吸引性的。这可以解释广义相对论引出的宇宙学疑难，量子引力在产生吸引力的同时，也产生着斥力；所以宇宙快速膨胀的原因也是量子引力的一个效应，不必是大爆炸的产物。

我们的宇宙没有起点，也没有终点，而是一个超级宇宙中不断波动着的一个超级基本粒子。这体现了马克思主义宇宙观的回归，无数与我们的宇宙类似的超级基本粒子组成了超级宇宙，而这个超级宇宙确实是无边无界的。
二次量子化

量子细胞场论使我们隐约看到了另外一种对称性，回答诸如为什么核力与电弱理论的不变群都是SU(2)，为什么味对称群和量子色动力学规范群都是SU(3)等问题。

强力与引力都有非局域性(Non-Local)特征，这些是传统的微扰方法无法解释的，比如说强力中的色禁闭和渐近自由现象，引力的非局域性引出的问题就更多了。因此我们认为强力和引力场都是在二阶上递归的力。引力有可加性，所以必须引入加法算符，但从逻辑上我们就知道这种引力理论一定是不可重正的，因为加法算符与递归算符是不相容的。但自然界中有很多二阶细胞的实例，也就是多细胞生物。直观的理解我们就知道量子细胞引力理论一定的超可重正的，注意这里的超可重正性与量子场论中的超可重正性不是一个概念。

这是因为多细胞生物有着全息效应，即每一个细胞中都含有全部的遗传信息，随便选取一个细胞就可以克隆出一个完整的生物体。回想马德西纳(Maldcena)关于量子引力与规范理论对偶性关系的那篇著名文章基于的前提也是全息原理，大自然是多么了解人的心思，现在越来越多的细节都走到一起来了。

酉模仿射群空间是不完备的，需要添加射影补丁，也就是无穷远点后才是完备的。当我们退回射影空间，想进行二次量子化时，发现一个完备的空间必然是同时具有双曲几何与椭圆几何性质的空间；用向量丛的语言来说，就是垂直空间满足反对称关系，水平空间满足对称关系，水平空间正确地复制出了爱因斯坦引力论；量子场论中对应的关系是费米子满足反对称统计，玻色子满足对称关系。

这种具有双重特点的空间蕴含了由于对偶关系引出的超对称性，双曲变换群与椭圆变换群都是保持二次的绝对形不变的群，引力的这种奇特效应是射影空间中线-线对偶关系引出的；翻译成物理的语言就是说，两个实物粒子通过交换引力子产生引力，对偶地，两个引力子也可以通过交换实物粒子产生斥力。

射影空间中的无穷远点与普通的点并没有本质的区别；投射回物理空间，荷也就是无穷远点却有可能是一个奇点，这也从另外一方面说明规范粒子一定是无质量的，只有无质量的粒子才能到达无穷远的边界点；空间的双曲几何性质也是量子场论中无穷大产生的根源，沿着一条无穷长的线积分肯定会产生奇异性，不过这种奇异性与黑洞的视界一样不是本性奇点，可以通过一个适当的变换消除，所以我们推荐用动态重正化方法代替量子场论中的静态重正化方法，象弦论一样彻底消除积分的发散性。

无穷大是量子场论的一个包袱，量子场论是不自洽的，我们这种几何上的事后诸葛亮式的论证提示了无穷大的起源，将无穷大变换成射影空间中的无穷远点，从而量子细胞场论在逻辑上是自洽的。另一方面，由于有了无穷远点，量子细胞场论和马德西纳理论站到了同一条起跑线上，但马德西纳理论却需要另外的5个维度，另外对偶性是量子细胞场论的基本原理，应该能导出很多有趣的结论。
简单的就是最好的

量子细胞场论大大简化了传统量子场论用到的数学。与幂零(Nil-potent)Dirac场方程用到的数学差不多，递归条件已经蕴含了费米子场是幂零的。

加进了二阶加法算符后，计算机逻辑中有一个对应的逻辑，即并行逻辑。由并行重写系统逻辑可知，当真空是反屏蔽时，自然可以通过重正化群导出不动点。但量子细胞场论与量子色动力学有一个差别：量子色动力学中是由重正化群导出不动点；而量子细胞场论中不动点是事先存在的，重正化群可以由不动点生成；也就是说，禁闭相、渐近自由和不动点在量子细胞场论完全是同一个原因引起的。幂零Dirac方程指出，强力可以不是由有色力传导的，要想了解详情可以参考有关幂零Dirac方程的原著(arxiv.org/abs/quant-ph/0301071)。因此，量子细胞场论完全可以解决强相互作用中所有的疑难。

引力引出的疑难有三个方面，宏观的、微观的和黑洞的。前面我们已经说过，传统的重正化方法在量子引力中是决不会奏效的，那么重正化群又如何。如果将强力比喻为量子世界中的植物的话；引力则像是量子世界中的动物，它们不会呆在一个地方不动，所以试图用不动点理论解决引力的问题也是不可能奏效的，只有超可重正性能够挽救引力。

超弦(Super-String)理论是为解释强力诞生的，由于量子色动力学的成功，超弦发展为试图解释引力。量子细胞场论在解释引力方面与弦论是有联系的，递归条件引入了一种回归效应，对应着开弦。由于没有了不动点，我们只能退回到射影空间找不变性，我们能够找到的是那些保持绝对形不变的射影群，即爱因斯坦群。爱因斯坦群在物理空间中的对应物不是别的，正是弯曲的时空，我们看到量子细胞场论与广义相对论的兼容性是多么好。那么绝对形在微观世界的对应物又是什么，不是别的，正是我们在超弦理论中熟悉的闭弦。

我们看到了弦理论的回归，不过量子细胞场论没有手征性问题、没有超对称的问题，因此没有必要像超弦理论一样需要引力额外的时空维度再让它们卷缩起来。量子细胞场论回归的正是当年那个朴素的弦理论。量子细胞场论一方面继承了量子场论中点粒子的看法，另一方面由于量子细胞的自对偶性，可以在空间中延展开，这同弦论的看法是一致的。
几何学上的推演

回顾一下我们的推导过程，我们尝试用量子场论的秘密武器重正化和重正化群去解决量子引力问题，却发现有一条行不通定理在等着我们，我们只好退回到射影空间寻找答案。当将射影几何推广到射影丛时，由于引力具有可加性，Klein几何自然会推演到Cartan几何，相应的引力理论称为爱因斯坦-Cartan理论，相应的联络称为自旋联络，微分算符称为Dirac算子。

我们看到，非对易几何与弦论的思想都有可取的部分，当我们尝试将自旋联络量子化时，我们发现，那不是别的，正是闭弦；非对易几何与弦论竟然分别是量子细胞引力理论的低能和高能极限。非对易几何是一种背景无关的理论，弦论是一种背景相关的理论，量子细胞引力理论正是这两种理论中间缺失的那道桥梁。量子细胞引力理论就这样自然地将非对易几何与弦论正确的部分统一了起来，由于这一系列推导过程都是自然的演进，所有的过程都是强制性的，我们根本没有其它可选项；由此可知，量子细胞引力理论一定是正确的。

量子场论中的概念	量子引力中的概念
电荷	引力荷
Gamma代数	Grassmann代数
费米子	超费米子(双曲几何的边界)
泡利不相容原理	超泡利不相容原理

坐标丛的截面是一种反对称的微分形式，满足Grassmann代数规则，其实有一种我们非常熟悉的Grassmann代数的特例，就是满足费米-狄拉克统计的费米子。可以引出的一个结论就是，由很多费米子组成的超费米子满足超泡利不相容原理。这是从广义相对论无法推导出来的，因为广义相对论只考虑了曲率没有考虑饶率，质量是曲率的源，而自旋是饶率的源。

这可以消除奇点疑难，黑洞不会永远塌缩下去而变为奇点，奇点是由广义相对论推导出来的一个幻像。一方面从质量方面来看，很多费米子组成的超级实物粒子满足超泡利不相容原理会阻止黑洞塌缩；另一方面，从能量方面来看，随着黑洞内能量的升高，会有越来越多的费米子组成共振态的复合粒子，这些复合粒子是非常短命的，马上就会通过强相互作用或电弱相互作用衰变而释放出能量，这种作用产生的排斥力甚至超过第一种作用。为了方便起见，我们将第一种称为质量不相容原理，第二种称为能量不相容原理。

在广义相对论中，质量和能量是等价的，而在量子力学中，质量和能量起到的作用是不等价的。这也提供了解决黑洞疑难的一个可能答案，就是黑洞的质量可能有一个上限，质量不相容原理能够阻止黑洞塌缩，使黑洞维持在一个动态平衡的状态；而当黑洞的能量超过一个上限以后，能量不相容原理开始起主导作用，当排斥超过吸引后，会引起黑洞爆炸。我们猜想遍布于宇宙中的Gamma爆可能就是黑洞爆炸引起的。
一个最简单的统一场论

量子细胞场论对费米子看法的改变不大，Dirac场位于一个二点离散空间与紧致空间的张量积空间中，构成了一个二叶(Two-sheet)不连通空间，电子就这样疯狂地在二个不连通空间中以27M每秒的速度跳来跳去，在量子细胞场论中电子就没有这么疯狂了。

对玻色子的看法改变就很大了。以电磁力为例，光子只有自旋为1或-1的状态，没有自旋为零的状态，但实际上，库仑力主要是由这个自旋为0的标量光子传导的，所以需要添加鬼粒子抵消该项多余的贡献才能恢复幺正性。在射影几何中有点线对偶性，自然可以得到一个自旋为0的标量粒子，但现在电磁力变成了一种内蕴的性质，考虑到黎曼几何是一种内蕴的几何，这就为我们建立统一场论奠定了基础。

爱因斯坦的相对论实际上还是一种绝对时空观，因为闵可夫斯基空间是一种伪欧氏空间，所以广义相对论也会产生牛顿引力论相似的悖论，实际上牛顿引力论也可以看成是弯曲时空的引力论，只要做一个坐标变换就可以了；引力子也是引力场的源，这种自吞性的集合在逻辑学上是被禁止的，哥德尔不完备定理可以体现这一点。所以广义相对论会产生很多悖论，比如空无一物的反de-Sitter空间会膨胀和时空奇点等。

量子细胞场论认为只有相互作用时时空才会弯曲，考虑时空中两个粒子交换一对标量引力子。对电磁力来讲，正电荷与负电荷是一对对合的点，我们自然也要求对标量引力论而言，两个粒子的位置也必须是对合的；这是量子力学所要求的，希尔伯特空间是一个平方可积空间，幺正性要求可观测量必需是自伴(self-adjoint)算子。这样我们就建立了一个能够正确产生出牛顿引力论的标量量子引力论，同时这个引力论也是与狭义相对论兼容的。

站在今天的立场你可能会反驳说，自旋为0同时质量为零的标量粒子从来都没有观测到。但时光倒回一个轮回(60年)，也就是中华人民共和国成立那年，假如爱因斯坦坚持时空的相对性，同时不是坚信“上帝不掷骰子！”他老人家很可能会发现这个简单的逻辑上自洽的统一场论，要知道那时人们还不知道弱力和强力。并且简单统一场论是纯几何的，爱因斯坦一定喜欢。力产生的原因是纯量子力学的，类似于两个原子通过交换电子从而构成化学健。我们将自旋为0的引力子称为牛顿引力子。

广义相对论中，实物粒子与引力子服从同样的方程，从现代量子场论的观点来看显然是病态的。量子电动力学中，电子与光子服从不同的方程，光子以最小耦合方式耦合进电磁场。简单统一场论中实物粒子与引力子服从不同的方程，引力子以最小耦合方式耦合进引力场，引力子的方程在复数空间中满足谐和坐标条件，我们知道这相当于电磁场的达朗贝尔方程。在射影空间中，点与线是对称的，这在电磁场理论中相当于电荷与电流密度的对称性，可以引出电流连续性方程；因此，简单统一场论中，引力荷与引力流密度也是对称的，可以引出引力流连续性方程，牛顿引力论和广义相对论都忽略了这种对称性。

完整的统一场论

简单统一场论与现代的观点有很多不谋而合之处，这难道仅仅是巧合吗? 简单统一场论是规范不变的，规范不变性是由点线对偶性导出的。时空是五维的，用以构造射影空间中的齐次坐标，不过这多出的一维纯粹是为了计算引入的，并不对应真实的物理维度；就像是量子场论中引入的鬼粒子，它们的存在只是为了恢复幺正性，并不对应真实的粒子。同时通过射影空间的对偶性我们发现了一条重要的关系：力=对偶性。量子场论中只有一种对称性，即洛伦兹对称性，而对偶性可以有很多；比如蜜蜂和花之间没有对称性而存在对偶性，蜜蜂有着朝花飞去的倾向，我们说蜜蜂和花之间存在吸引力。不过量子细胞显然没有生物细胞那么复杂，量子细胞只需要携带能够产生四种基本力的遗传信息就足够了。

这与那个神秘的M理论的中心观点不谋而合，传统量子场论从对称性出发，认为力的根源在于对称性，从后现代观点来分析这是有问题的，对称性引出自旋为1的光子，而实际上自旋为1的光子并不是库仑力产生的真正原因，库仑力的真正起因是标量光子。现代量子场并不排除自旋为0的无质量引力子的存在，例如通过真空自发破缺可以产生自旋为0的无质量粒子，只是这些无质量粒子都被中间规范玻色子吃掉了。

标量量子引力理论还需要扩展，原因是引力子还会与光子耦合，自旋为0的粒子不会与光子耦合，所以引力子的自旋必须是2。直接对广义相对论中的度规量子化是不行的，原因是广义相对论中的度规是非线性的，对联络量子化是可行的，沿着一个封闭的圆圈对联络积分可以导出一个不变曲率，实际上圈量子引力正是基于这种思想发展出来的，Yang-Mills场也可以通过这种方式量子化从而导出瞬子解。但圈量子引力面临着一个尴尬，必须从联络导出度规，而圈量子引力理论做不到这一点，引力虽然量子化了，却无法证明这个量子引力论与广义相对论的兼容性。量子细胞场论没有这个问题，原因还是在于对偶性，类似于简单统一场论中的方法，实际光子的状态是自旋为1的光子和标量光子的混合状态。

自始至终我们都是沿着一条唯美的思想导出了统一场论的所有规则，怎一个美字了得，难道这一切不是必然的吗? 现在可以肯定的是粒子就是自对偶的量子细胞，量子细胞带有极性，极性是力的根源，极性满足很好的代数规则，对费米子而言满足费米-狄拉克统计，对玻色子而言满足爱因斯坦-玻色统计。还有就是极性可以满足布尔代数中的吸收律: A+A=A和消去律AA=A；比如你是一位由1万亿只细胞组成的小姐，虽然每只细胞都带有小姐的遗传信息，但只要一个量子数就可以表征了；量子力学中也有这样一个例子，费曼的路径积分法认为粒子经由所有可能的路径由一点到达另外一点，但这些所有可能路径的贡献加在一起仍然是只要由一个量子数表征就足够了。

量子场论的先辈们显然忽略了吸收律，先辈们小心翼翼地摸着石头过河，可能根本没时间停下来欣赏大自然的美丽；我们却可以踏着先辈们的足迹幸运地发现隐藏在大自然背后美丽的数学定律。吸收律在量子场论中就有直接的应用，以特Hooft的大N展开为例，假如色荷满足吸收律，那么N种颜色的量子色动力学就与3种颜色的量子色动力学是等价的，但N种颜色的量子色动力学的耦合常数可以很小，适合在微扰论的框架下进行计算。另一方面，如果费米-狄拉克统计和爱因斯坦-玻色统计关系成立的话，吸收律就意谓着超费米-狄拉克统计和超爱因斯坦-玻色统计也是成立的。

从吸收律出发也可以推断出引力场也是一种自对偶的场，我们都很熟悉一种自对偶的场，就是电磁场，因此可以以量子电动力学为模板稍加改造发展出带“权重”的引力场的量子理论。回想弱相互作用理论和强相互作用都是以量子电动力学为模板发展起来的，难免有一种英雄所见略同的感觉。

较为深刻的结果

简单统一场论通过最小耦合方式将质量与质量荷的作用分离开，可以推导出一些较为深刻的结果。首先，同牛顿和爱因斯坦引力论不同，引力耦合常数变为无量纲的，我们知道费米弱相互作用理论是不可重正化的，原因在于费米耦合常数与牛顿引力耦合常数有相同的量纲，所以需要引入Yang-Mills规范场和中间矢量玻色子使得弱耦合常数无量纲。

我们还是从Weyl引入规范场最初的原理出发，证明简单统一场论确实是自洽的。考虑平面丛，由平面到平面的变换是10参数的群，当底流形为洛伦兹流形时，这个变换群与洛伦兹群是同构的。平面与平面之间可以定义联络和曲率式，当底流形为洛伦兹流形时，我们知道这正是电磁场的联络，详细的证明可以参见陈省身老先生的演讲。

简单统一场论满足可重正化最重要的条件，当实施一个标度变换后，与电荷一样，引力荷没有发生变化，感觉简单统一场论应当是可以重正化的，但这需要一个严格的证明。

这里，重正化的意思是简单统一场论是局部可重正的，用微分几何的话说，在切空间的一个邻域内是可以重正的。注意，简单统一场论是一次量子化的，所以可重正性并不是必须的，但局部可重正化意谓着在微扰论的框架下理论可以跑得更远，可以计算出一阶或二阶以上微扰引出的修正，所以还是有实际意义的。

引力还有整体性质，仅有局部重正化是不够的。原因在于，规范场论中的众粒子生活在一个“众生平等”的“民主社会”里，所以局部重正化就等于整体重正化；而引力中的众粒子还可以生成复合状态，像是生活在一个“弱肉强食”的“集权社会”里。另一方面，引力荷不是一个拓扑整数，二次量子化时不是一个好的量子数；所以只有当证明了引力在整体上是超可重正化以后“复杂”统一场论才是真正自洽的。

看起来真的如马德西纳(Maldcena)猜测的那样，五维反de-Sitter空间中，量子引力与规范场论是对偶的。不过与空中楼阁式的马德西纳理论不同，我们的理论是脚踏实地的；我们认为爱因斯坦的质能关系式反映的是隐藏在对称性背后的对偶性，这有些间接的证据，例如强子的质量谱近似地成一种线性的关系。从质能对偶性出发，就可以得出量子引力可能与强力对偶的关系，前提是强力的根源必须是能量，而强力看起来确实是能量引出的，比如具有比约肯标度不变性。

对偶性

射影空间没有直观的角度和距离的概念，实际上我们的构造中已经隐含了定义角度和距离所需的元素。弦论离不开超对称性，因为引力子的自旋为2，必须有一个将玻色子转换为费米子再转换回玻色子的操作；而在量子细胞场论中，荷是空间的无穷远点，在射影空间中无穷远点与普通的点没有什么区别，只需简单的直射变换就可以将无穷远点变成普通点。

由拉盖尔公式可以知道直射变换构成的群是SO(2)群，同构于电磁场的规范群U(1)群，对的！但拉盖尔公式将荷变换到对偶荷形成的角度是180度，有问题的! 我们知道电磁场的波函数在转过了360度后能够保持不变。当然我们已经知道答案了，就是引进对偶的磁场，在射影空间中就相当于用对射变换代替简单的直射变换，并且群的性质并没有被破坏，对射变换构成的群称为广义射影变换群；在广义射影变换群作用下，电磁场波函数转过360度保持不变。

引力子的自旋为2，在转过了180度后波函数不变；可见引力荷必须同时带有引力电荷与引力磁荷，这样转过180度后，引力电荷变成引力磁荷，而引力磁荷变换为引力电荷。对于低速运动的有质量的物体，吸引力主要是引力电荷引起的，可以得到牛顿引力论的结果；对于光线，引力电荷与引力磁荷同时发挥作用，需要将椭圆几何中的对径点等同起来，所以太阳引起的光线偏折是牛顿引力论计算出的结果的2倍。我们看到，在低能区量子细胞场论与广义相对论的结果是一致的。量子细胞场论改变的是对引力在高能区的看法，广义相对论在高能区的结论是病态的，实际上弦论改变的也是对高能区的看法，但弦论的问题是不能确定在低能区与广义相对论的对应关系。

现在我们知道为什么自然界中没有无质量的标量粒子了，由对偶性导出的标量粒子总是被隐藏在对称性当中；在电磁场中，标量光子总是被隐藏在矢量光子中，这相当于Gupta-Bleuler量子化方法，但Gupta-Bleuler在数学上很复杂，而量子细胞场论用到的数学要简单得多。在量子细胞场论中，自旋为1的纵向分量有点像铁环，而自旋为0的纵向分量像是铁环滚过的路，铁环滚过路面，它们的纵向分量有一部分恰好是抵消的，剩余的部分就是库仑力，只是自旋为0的纵向分量构成的路面只为铁环本身而存在，这是狭义相对论的基本原理。Gupta-Bleuler需要使用不定度规，这本质上还是一种欧氏空间思想的残余，而在量子细胞场论的射影丛中，本质上各个点都是平权的，就不需要使用不定度规了。

近代物理实验有证据表明，在高能区，四种基本力的跑动耦合常数也可能会相交于一点，也就是说，可能有一个统一的耦合常数；不过我们不打算深究这个问题，还是暂时留给量子场论专家们伤脑筋吧。我们看到，由电磁力到电弱力到引力，在量子细胞场论中，大自然的四种基本力呈现出一种等级结构，在这方面，它们的确是统一的；电磁力是一种保持退化点x=0不变的力，弱力是一种保持二级退化曲线x±iy=0的力，引力是一种保持绝对型x²+y²=0不变的力，前一种力是后一种的退化情形。

说到对偶性，量子细胞场论完全可以称为对偶场论，不过量子细胞是我们逻辑推理过程中重要的路标，能够提供我们物理上直观的图像，一旦我们获得一个数学上等价的描述，就可以将路标拿掉。回到电弱统一理论，对称性生成了一个自旋为1的无质量矢量粒子，对偶性给出了一个自旋为0的标量粒子，那么规范玻色子是如何吃进标量粒子而获得质量的呢？答案还是在对偶性，对于低速运动的电荷，电场也就是电力线是像刺猬一样布满整个三维空间中的，假如我们强迫电荷以光速运动，那么电场就紧缩到与运动方向垂直的一个平面上，相应的图像在很多电动力学的教科书上都可以找到。

射影空间中还有点面对偶性，在洛伦兹群作用下可以保持质心荷不变，就样就形成了一个平面丛；量子场论中，自旋为1的粒子自由自在的旋转，没有圆心的概念，用量子场论的话说，自旋只能取值1或者-1；加进了点线对偶性后，我们发现，量子细胞场论中自旋为1的粒子可以围绕一个由对偶性生成的圆心旋转，这样就将无质量的标量粒子吃掉了。量子细胞场论中，光子具有三个分量；而在量子场论中，光子只有两个分量，要么使用洛仑兹规范，要么使用库仑规范；量子细胞场论中我们将洛仑兹规范和库仑规范有机地组合在了一起，量子场论中似乎会把所有事情弄糟的鬼粒子在量子细胞场论中也不必出现了。对于电弱统一理论，由非对易几何可以得知中间矢量玻色子的质量不过是一种“电弱磁”效应，根本不需要Higgs粒子的参与；由对称性原理出发的量子场论无法导出类似的结论，量子细胞场论可以得出与非对易几何类似的结论，但我们的推理很简单，非对易几何用到的数学非常复杂，估计会吓退很多希望投身于统一场论研究的人。

回想地心说时代，人们发现很多星星的观测轨道与理论不符，只能加进一个一个的本轮试图自圆其说，到了哥白尼时代，开普勒发现行星的轨道可以不必是圆，还可以是椭圆。酉模仿射变换具有保持平行性和面积不变的特点，在相当于开普勒行星运动第二定律。假如我们允许中间矢量玻色子也可以沿椭圆旋转，质量隙就自然地显现出来；再者，如果玻色子的轨道是抛物线型的，就可以解释弱相互作用下的CP破缺问题。不过量子细胞场论中不需要一个充满Higgs粒子的背景场，点线对偶性引出的光子的纵向极化分量满足的方程类似于声波的方程，所以我们也可以将量子细胞场论中的标量光子称为声子，不过这和量子场论中的声子有一个很大的不同，量子场论中的声子属于集体激发模式，也称为元激发，需要一个背景场的参与；而量子细胞场论的声子完全是由狭义相对论基本假设引出的，属于场的基态；之所以产生这种差别的原因在于，量子场论中的闵可夫斯坦空间是不完备的，而量子细胞场论中的爱因斯坦空间是完备的。

这样我们就给出了一个质量隙起源的较完美的答案，不要小看这个问题，它与庞加莱猜想、NP完全问题等并列称为二十世纪七大难题之一，美国的克雷数学研究所对每个问题分别悬赏100万美金。想当年刘维尔洋洋洒洒地写了几十页纸终于证明了零基定理，不料被Hilbert短短的几名话就重新证明了，刘维尔不无感慨地说：“这不是数学，是神学!”现在的问题是假如我们是对的，我们这种看似“神学”的证明是否应该得到那100万美金的悬赏?
“乌云”消散了!?

洛伦兹群是酉模仿射群，仿射空间是不完备的，连欧氏空间中最简单的圆都无法定义；但欧氏空间中有讨厌的绝对原点，就是本性奇点；返回到射影空间，我们又可以定义圆了。欧氏空间是内积空间，量子力学需要内积的概念，因为Hilbert空间是内积空间；量子场论也需要内积的概念，因为量子场论中最基本的不变自由拉格朗日量是场强张量与对偶场强张量的内积。非对易几何引入了一大堆数学概念，最终找回了内积空间，而量子细胞场论中内积是很自然地定义的；如果非对易几何的创始人Alain孔涅知道了量子细胞场论中如此简单地推导出了内积的概念，一定也会感慨“神学”的威力吧!

引力的自由拉格朗日量是引力场强张量与对偶引力场强张量的内积，由于引力场强张量产生的是正确的爱因斯坦引力论，那么对偶引力场强张量产生的力一定是排斥性的反引力，这就解释了宇宙中为什么会有暗能量的存在。这也说明了爱因斯坦引力论的局限性，因为广义相对论不是一种规范理论，这与规范场论的中心思想是互相抵触的，所以正确的引力论一定是爱因斯坦-cartan引力论。

考虑一下强力，夸克等价于量子细胞，量子细胞通过交换胶子产生相互作用，在这一点上量子细胞场论与量子色动力学的观点是一致的。我们说爱因斯坦的质能关系式反映的实际上是一种隐藏在对称性背后的质能对偶性，我们将高能区的核子比喻为鸡蛋，将低能区的核子比喻为已经孵化成型的小鸡；在高能区，夸克主要由能量构成，它们之间是渐近自由的，在低能区，夸克主要由质量构成，它们之间的相互作用力会很大；这一点上量子细胞场论与量子色动力学仍然是一致的。

对偶的学名是正交补，熟悉量子逻辑的人一定知道，量子逻辑的学名应当是正交补逻辑。当由对称性产生对偶性时，对称性破损了；在射影空间中洛伦兹空间是对称的，但当映射到仿射空间中时，费米子一定要取三个空间方向之一，所以夸克可以是无色的，只要空间量子化就够了；我们还要加上一个递归条件，这不是一个很强的限制，就好比一队士兵听到齐步走的命令后以统一的相位运动，这不是很难做到的；但这样夸克的分布变得有规则起来，相邻的夸克必然是反平行的，这样空间就超导化了；量子色动力学中的重正化群只能给出一维的重正化流，量子细胞场论中核子可以有三维的结构；Yang-Mills场是非线性的，线性化的代价是核子的质量有一个上限，这个有限的质量正是色禁闭现象的根源。

这不正是特Hooft关于色禁闭猜想的最佳答案么? 量子细胞场论中的二次量子化已经隐含了递归条件，所以一切的推导都是自然的；Seiberg-Witten理论也可以给出类似的答案，代价是必须引入无法证实的超对称性和一大堆复杂的数学。并且量子细胞场论中的核子呈现出饱和性，这与核子物理的液滴模型和MIT袋模型的看法是一致的。我们还附带地解决了一个古老的先有鸡还是先有蛋的问题，鸡和蛋是相互对偶的场，如果你去测量核子的话，得到的只能是鸡和蛋的一个混合态。不引进任何外来的夸克质量，量子色动力学能够给出核子质量的绝大部分，不过，由于它只能给出核子质量的93%，因此只能粗略地给它打93分；现在量子细胞场论中由于对称性破损使圆变成椭圆，夸克获得了质量，能打到100分了。

尽管粒子物理标准模型和带暴胀的宇宙学大爆炸模型的建立表明基本物理规律的研究已取得了极其辉煌的成就，但仍然存在着不少极其重大的未解决的问题。在今天，在基本物理研究的天空中，究竟存在着哪些重要的“乌云”呢？李政道教授在2000年国际弦理论会议上的讲演中提出了四大问题：一、宇宙的暗能量和暗物质问题。二、引力的量子化问题。三、色禁闭问题。四、自然界是否存在着更大的对称及更基本的统一理论。我们看到李政道教授提出的四大问题在量子细胞场论中都得到了圆满的解答。

对偶性的结果

由于狭义相对论是爱尔朗根纲领的一个特例，Felix Klein(不是弦论中的Klein，更不是编写〈古今数学思想〉那个Klein)成了狭义相对论最早和最坚定的支持者。1974年，杨振宁明白了规范场是标架丛上的联络；于是，陈省身认为统一场论的基础一定是这些几何上的数学概念。沿着这些数学思想发展，我们将Klein几何与矢量丛的概念结合在了一起，发现果然是硕果累累。我们在没有引入任何新的假设的前提下用几何的语言重写了量子场论，我们唯一的假定是统一场论一定是很美的，也就是空间一定是完备的。

对于引力而言，如果引力满足规范对称性，就会演变到爱因斯坦-cartan引力论，我们对自旋联络量子化，发现引力必定满足超泡利不相容原理，这就解决了奇点问题。引力场必定是一种自对偶的场，这相当于M理论中的S对偶性，用S对偶性可以解释暗能量问题，因此如果M理论可能是对的，量子细胞引力论就一定是对的。其实广义相对论的问题不止有宇宙学难题，太阳系所处的银河系是一种旋臂结构，这用广义相对论和弦论都是无法解释的，量子细胞引力论有可能解决这个问题，但这需要有一个严格的证明。

量子场论中的对称性自发破损一词有误导的成份，我们知道对称性自发破损等价于量子细胞场论中的点线对偶性，对于电弱统一理论而言，手征对称性破损之后是不需要恢复的，而对于量子色动力学而言手征对称性破损之后的自发恢复至关重要；迄今为止，尚未有人能够给出手征对称性自发破缺的数学证明，但从这一破缺方式已经得到了大量的间接证据；这在量子细胞场论中根本就不是一个问题，我们不仅很容易证明手征对称性的自发破缺，而且还很容易导出手征对称性破缺之后的恢复机制，它们不过是递归条件而已。量子色动力学对π 介子及其它假Goldstone 粒子质量的计算虽然很漂亮，但从回答本原问题的角度看却仍不足以令人满意；量子色动力学为质量起源问题提供了一个独特而接近完美的回答，为了寻找更接近满分的答案，我们不得不重新回到标准模型中不能约化的那些质量上来。那些质量究竟来自何方？究竟还能不能约化？这些问题的答案只能从量子细胞场论中寻找了。

广义相对论中的引力耦合常数是有量纲的，可以预计的是广义相对论在高能区的行为一定是不好的，弦论改善的是在普朗克尺度下引力论的奇异行为，弦论回避了量子场论中的重正化方法，但这也使弦论与量子场论的兼容性打了折扣。费曼称量子场论的重正化方法是一种“脑筋不正常的运转”，但是这种“将垃圾扫到地毡下藏起来”的做法实际上是对的，并获得了物理实验的支持。量子细胞场论直面了重正化的问题，量子场论中的标度行为涉及到的群是共形群，生成元是一种称为伸缩子的东西；仿射空间中也有伸缩子，牵涉到的变换群称为相似变换群；实际上Weyl在最初的规范场论中用的正是相似变换群。

由点线对偶性生成的是规范场的纵向极化分量，在量子场论中规范场的纵向极化是不需要重整化的。由相似变换群生成的规范场却需要小心处理，一方面相似变换违反量子力学中波函数的归一化要求，这也是Weyl最初的想法被抛弃的原因，这在量子细胞场论中是不难处理的，我们处理的是在空间中每一点上定义的纤维丛，只要伸与缩是对偶的就可以解决波函数归一化问题；另一方面，生成引力的是保持一对绝对对合点不变的变换群，正是相似变换群。看来Weyl最初的想法并非一无是处，只是用错了地方。
Yang-Mills理论与质量隙猜想(Mass Gap Hypothesis)

物理始终是新数学理论之灵感与动力的来源，自微积分的发展历史以来，好的数学一直是受物理之激励才有更好的发展，物理中产生的数学问题解答及方法，从过去到现在，一直是数学活力的来源。物理在某种意义底下提供了数学最深刻的应用。Yang-Mills 方程起源于量子物理，是由著名华裔物理学家，诺贝尔奖得主杨振宁与 Robert Mills所发现。

我们说物理定律是“对称的”，意思是我们可以对物理定律或者对我们表达物理定律的方式做一些事，结果没有任何差异。对称说明了那些没有改变或不能发生的事，所以对称是现代物理学的动力。德国数学家 Hermann Weyl (1885-1955)给对称(symmetry)下了一个绝佳的定义：「假如你对某件事物做了某些事情(operation)之后，它看起来和原来完全相同，那么它就是对称的。」在数学中常常把不变性(invariance)称为对称性。Hermann Weyl 曾说：「我的研究工作尝试把真理与美统一起来，可是如果要我在两者之中择一的话，通常我都选择美。」其实他心中的美就是对称。当数学应用到物理时，美学判断的有效性最为可观。数学家在他们的研究中，受到结构美之概念形式的强烈期望所驱使，是相当平常的。

早年把「对称性、不变性及守恒量之间最关键的联系」结晶成形，为爱因斯坦发展广义相对论铺路的是德国女性数学家Emmy Noether (1882-1935)。在广义相对论发展之初，人们发觉(表面上看来)在弯曲的四维空间中，能量是不守恒的，这是一个理论基础上的缺陷。Noether把这问题解决了，她利用对称性证明弯曲的四维空间之能量是守恒的。对她而言，把对称性与基本自然律联系在一起的理念是非常自然的Noether对于对称性与自然律的构想，给了美与真理之间一个最具体的链接。科学里认为的美，与贝多芬音乐中的美是同样的东西！

基础物理发现的第一个重要的对称性是Lorentz 不变性(经Lorentz 变换后不变)。这是作为Maxwell 方程的数学性质而被发现的。爱因斯坦就是以Lorentz变换为基础而发现狭义相对论，后来再加以推广，由广义坐标不变性的想法，加上等价原理，导致了广义相对论。对称性也导致英国物理学家诺贝尔物理奖得主P. Dirac (1902-1984)把狭义相对论与量子力学以数学方法合并在一起后(量子场论)，预测反物质的存在。这后来是由美国加州理工学院的安德森由实验证实，并因此荣获诺贝尔物理奖。因此藉由对称性可以帮助我们〝看〞到物理现象，从此就不在黑暗中摸索。

早在二十世纪初(1918-1919) H. Weyl为着讨论电磁力与引力之对称关系，提出所谓“规范不变性”(gauge invariance)之概念，但是要到 1954 年杨振宁与 R. Mills 提出的“Yang-Mills 规范理论”，才是真正的突破。杨振宁由数学入手，提出一个规范性的理论架构，后来逐渐发展成为量子物理最重要的理论之一，也使得他成为替近代物理奠基的一代大师人物。

杨振宁与 R. Mills提出的理论，会产生传送作用力的粒子，但是他们碰到的困难是无法解决这个粒子的质量的问题。他们从数学推导的结果是，这个粒子有电荷但没有质量。因此困难是如果这一有电荷的粒子是没有质量，那么为什么没有任何实验证据呢？而如果假定有质量，规范对称性就会被破坏。一般物理学家是相信有质量，因此如何填补这个漏洞(gap)就是深具挑战性的数学问题。

规范场方程(Yang-Mills equation)是由电磁学的Maxwell方程而来。1974年杨振宁又发现了这些方程式与微分几何大师陈省身研究纤维丛理论(fiber bundle theory)中的陈示性类(chern class) 有密切的关系。物理学者因而知道有了解陈示性类的必要。这实在是令人惊讶的地方。至于为什么自然界的各种力都建筑在几何学中的纤维丛观念上，始终是个未解之谜。

从历史的发展而言数学渗入广义相对论与规范场理论的过程是全然不同的。爱因斯坦没有黎曼几何(Riemann geometry)就不可能写出广义相对论方程式。就后者而言，规范场方程式早已写出来了，但后来是透过数学才了解其深意。由于杨振宁的影响，Yang-Mills方程已向数学界渗透，并导致许多优美的数学成果特别是拓扑学(topology)的惊人突破，S. Donaldson为此荣获1986年的费尔兹奖。另外则是英国数学家阿提亚( M. F. Atiyah)与美国数学家辛格( I. M. Singer)关于瞬子(instanton)即Yang-Mills方程的自对偶解的工作。

相对论与几何

对偶性是量子力学的基本假设，所谓正则量子化方法是指一对对偶的量，比如位置和动量算符的非对易算符；我们也知道，狭义相对论与量子力学是兼容的，这里蕴含了量子细胞场论与经典量子场论的一个重要区别，量子细胞场论认为真空真的就是空的；量子场论中那些由真空产生的效应，例如Casimir效应完全可以由自对偶细胞完成；但这里自对偶细胞只有局部的意义，不会扩散到整个真空。狭义相对论否认真空中存在背景场，量子场论是狭义相对论与量子力学相结合的产物，怎么会出现一个无限大的真空呢?

从几何的观点来看，爱因斯坦引力之所以与其他力无法统一到一起的一个重要原因是，引力存在于一个弯曲的时空里，而其他三种力存在于一个平直的时空中，而实际上这种传统量子场论的观点是有问题的；事实上从几何的观点看电磁力、弱力或强力也可以通过坐标变换，看成是弯曲时空几何产生的力。如果我们将大自然的四种基本力从几何的观点放在同一个空间中一起考虑，就可以得到一些必然性的结论。

将有质量粒子与无质量粒子放到一起看，狭义相对论引出的空间等价于双曲几何，具体的论证可参见费保俊所著的《相对论与非欧几何》一书，这样引出的是斥力；而我们知道引力是吸引性的，所以椭圆几何也是同时存在的；如何解决这个问题，回想费曼的观点，一个沿正时间轴方向移动的粒子必然会有一个沿逆时间轴移动的粒子相对应，所以我们说量子细胞引力中，引力和斥力是同时存在的，这里沿逆时间轴移动的粒子可以解释成霍金所说的沿虚时间轴移动的粒子，只是虚时间轴与实时间轴是一对相伴随的轴。

将有质量粒子与无质量粒子统一考虑，狭义相对论就否认了时空是平直的可能性，如果时空是平直的，那么光速就应该是无限大，这与狭义相对论原则是矛盾的；之所以出现量子场论中时空平直的论调，是与闵可夫斯基平直的观点相联系的；回想一下，闵可夫斯基就是爱因斯坦上大学期间称他为“懒狗”的那位数学教授，但爱因斯坦并没有坚持时空的相对性原则，广义相对论最终还是基于闵可夫斯基空间的。量子细胞场论也引出了一个问题，通过坐标变换现在四种力都是存在于弯曲时空中的，那与传统量子场论是如何兼容的，其实量子细胞场论早已解决了这个问题；回想一下，点线对偶性给出的几何就局部等价于平直的时空。

量子细胞宇宙学模型

考虑一种背景为四维de Sitter时空与四维反de Sitter时空的乘积的宇宙学模型，有质量粒子存在于一个背景为正的常曲率de Sitter空间中，引力子则存在于反de Sitter时空中；de Sitter时空是封闭的，构成了一个四维超球面，同时这个四维超球面又构成了反de Sitter时空的边界；我们知道反de Sitter时空中任何一点到达边界的距离都是无穷远，引力子是无质量的，只有无质量的粒子才能够到达反de Sitter时空的边界；引力子的测地线是反de Sitter时空中的圆弧线，这样一个双曲几何的模型是庞加莱在研究自守函数时发现的。

在引力场的最小耦合中有一个系数i，众所周知这个系数来自于量子力学，这个系数是爱因斯坦引力论中没有的，却是量子场论所必需的，这就意谓着有质量物体的场与引力子场是垂直的。这样一个宇宙学模型很明显有马德西纳猜想的影子，所以我们将两个名字合在一起，称这样一个时空为马德西特(Malde Sitter)时空。只是马德西纳猜想是个空中楼阁，而马德西特时空却是量子细胞引力论的一个很自然的推论；并且真实的宇宙很可能正是这样构成的。我们似乎又回到了地心说时代，不过这是引入了牛顿引力论和爱因斯坦引力论中正确思想以后的现代版地心说。

考虑一个稳恒态的宇宙和牛顿引力，我们知道牛顿引力势与粒子间的距离成反比，也就是与庞加莱双曲模型中圆弧弦的半径成反比；当距离很小时，量子细胞引力论引出的是牛顿引力的反平方律，可是随着距离的增大，量子细胞引力论导出的引力势呈单调下降的趋势；当两个粒子处于的位置位于椭圆几何的对径点上时，由于圆弧弦为直线，它的半径为无穷大，这两个粒子间的牛顿引力势为0；假设我们位于宇宙的北极点上，考查位于宇宙南半球的两个粒子之间的引力相互作用，它们之间确实存在的是引力，而相对我们而言存在的是斥力，这就解释了为什么离我们很远的星系看起来在快速离我们而去，要知道引力对光线的偏折作用比对普通有质量物体的偏折作用大一倍，这样就会产生强烈的引力红移，所以离我们很远的星系的红移是引力引起的。

量子细胞引力论中有一个欧氏空间的原点，也就是三个空间坐标和一个时间坐标都为0的点，不过有质量的物体是不能到达坐标原点的，只有引力子能够到达坐标原点，但引力子却是借道而过，因为对引力子而言不存在静止的参考系。在量子细胞引力论中，有质量物质场与引力子场遵守不同的场方程，而且黑洞与宇宙遵守的也是不同的几何模型，即单重椭圆几何与双重椭圆几何的差别，这是量子细胞引力论与广义相对论的又一差别。黑洞是有质量的，一种可能是黑洞永远无法到达坐标原点，除非黑洞变成一个巨型的引力子，才能从坐标原点借道而过，坐标原点永远也不可能成为奇点；或者黑洞大到足以吞下整个宇宙，这在量子细胞引力论中意谓着这种黑洞是不稳定的，几乎立刻就会反弹回去；所以如果宇宙是从大爆炸中诞生的，这不是从奇点上诞生的，宇宙有一个最小的体积，将整个宇宙压缩到一个黑洞里，不知道有没有人计算过宇宙的最小体积是多少；这意谓着量子细胞宇宙不需要一个古思所说的暴涨阶段。

还有一种可能是黑洞与宇宙是对偶的，黑洞会把椭圆几何中的对径点连接起来，从坐标原点借道而过，这就是广义相对论引出的所谓虫洞，这意谓着黑洞吸收的物质会从对径点上喷发出来形成所谓的白洞；这就好比在地球上开凿一个穿地心而过的隧道，从隧道的这头扔一个东西下去，有可能从隧道的另外一头也就是地球的另外一端重新冒出来；白洞有可能是我们观测到的类星体，现在我们知道类星体很可能就是离我们并不遥远的黑洞从宇宙的另外一端重新冒出来，所以类星体很亮，并且由于身处宇宙的另外一端，会伴随着巨大的引力红移。

简单统一场论

在Klein以后，法国数学家庞加莱给出了双曲几何的另一种模型，它可以应用到复变函数论里的一些重要结果的推论上；庞加莱模型仍然取圆的内部作用双曲几何的平面，却把垂直于已知圆周的圆弧作为直线；算做移动的是把圆变成自己的任何保角变换。庞加莱双曲几何模型为我们讨论统一场论提供了很好的平台，我们知道，庞加莱双曲几何不仅可以建立在超球面的内部，也可以建立在上半平面上，上半平面上的双曲几何对应的正是电磁场。我们让正电荷或负电荷沿上半平面的边界活动，与边界垂直的半圆弧是光子移动时的测地线，这里有个小问题，光子在内部空间移动的速度不是光速c，而是要乘上一个系数π/2，好在经过量子力学的长期熏陶，人们已经习惯了在各种抽象空间之间变来变去，所以不必太操心这个系数。现在与边界垂直的半圆弧的半径的倒数正是库仑势，这样利用庞加莱双曲几何模型我们有了一个电磁力和引力的统一几何模型。

从这个模型出发可以导出很多有意义的结论，利用我们铁环与路面的类比，我们知道在电磁场中位置和动量确实是对偶的场量；回想电磁场量子化的历史，简单地将电磁场量子化，人们发现与库仑势共轭的动量恒为零，于是才有了Gupta-Bleuler利用不定度规的量子化方法，细胞量子化方法与Gupta-Bleuler方法等价，并且提供了一个Gupta-Bleuler量子化方法的直观的几何模型。之所以选择庞加莱模型是与射影空间的特定性质有关系的，当我们将射影空间改造成度量空间后，移动了多少距离和转过了多少角度完全是对偶的概念；以引力为例，在de Sitter时空中即宇宙边界上的移动与在内部的反de Sitter时空中转过多少角度是对偶的。所以在量子细胞场论中，代表旋转的自旋为1的矢量分量与代表移动的自旋为0的标量分量完全是对偶的不可能分割的整体；而在传统量子场论中，这两种分量是分开来处理的。

费曼称量子电动力学中的无穷大是脑筋不正常的，从现实的角度出发我们也知道带着量子场论中没有物理意义的无穷大试图构建统一场论也是一件不可能完成的任务。既然在量子细胞场论中，位置与动量是一对共轭的场量，而无穷远点是位置的极限，无穷大是量子电动力学中动量的极限，可见最子细胞场论中的无穷远与量子场论中的无穷大之间确实存在对偶关系；量子场论牵涉到无穷大的加减乘除运算，就目前人类已经掌握的数学知识体系而言，只有射影空间中的无穷远是可以直接实施加减乘除运算的从而获得逻辑上自洽的结果，所以从量子场论发展到量子细胞场论在逻辑上的必然的，所谓自古华山一条路，人类还没有找到其它处理无穷的办法。

从量子场论发展到量子细胞场论，脑筋终于正常了！以下为了讨论的方便，我们将量子细胞场论中的爱因斯坦空间简称为理想世界，将量子场论中以闵可夫斯基空间为基底的物理世界称为现实世界；现在的问题是无穷远在射影空间中纯粹是一种数学构造，不一定代表着现实世界中的无穷远，但目前的量子场论告诉我们理想世界的无穷远可能真的也是现实世界中的无穷远，由于量子场论已经在很大的精度上被证实了，可以得到的结论是即使理想世界的无穷远并不意谓着现实世界中的无穷远，至少在目前观测范围内它们是大致相同的。

但现在还是有了新的物理。首先，时空在射影空间中拥有最大的对称性，需要最多的参数描述，而映射回仿射空间或闵可夫斯基空间后，参数自然会减少，用量子场论的话说就是对称性自发破缺了，可见如果我们沿用量子场论的对称性自发破缺一词纯属误称，因为量子细胞场论中的这种破缺不需要一种背景场，不过量子场论中属于误称的名词还有很多，这也反映了量子场论的先辈们在探求真理的道路上走的是一条充满坎坷的路；另外，点线对偶性给出的自旋为0的粒子的对称性是动态的，现在Higgs机制需要的两个要素我们都有了，所以量子细胞场论与Higgs机制也是兼容的，只是不需要Higgs背景场。

其次，量子电动力学中的截断被作为一种重正化的辅助参数引入，截断动量是随意引入的，至于截断动量数值的大小是没有实际物理意义的；量子色动力学中的重正化群理论部分地改变了这种看法，截断动量虽然没有绝对的物理意义，却可能有相对的物理意义，例如引出渐近自由的概念等等；量子细胞场论进一步改变了这种看法，原因在于理想世界中的无穷远点不一定是现实世界中的无穷远点，例如假设理想世界的无穷远点对应的不是现实世界的无穷远点而是截断动量的话，那么截断动量之上的物质就很可能是宇宙中的暗物质，这样我们就可以为暗能量和暗物质都给出一个解释；另外，低频截断对应的很可能是色禁闭效应；关于这方面我们将做进一步的探讨。眼下，将量子场论的重正化翻译成量子细胞场论中的无穷远的语言是有趣也是有意义的工作；例如我们可以证明量子场论确实是自洽的，从而解决这一困扰物理学界半个多世纪的难题，我个人认为凭这一成果获得诺贝尔物理学奖或者沃夫物理学奖也是应该的；Joking?

如果把时空的无穷远点看成是一个点，那么任何一个局域规范变换都可分解成一个整体规范变换和一个在无穷远点等于1的局部规范变换。局部变换下的不变性可以归结为格林函数的生成泛函要满足一个恒等式，通常称为Slavnov-Taylor恒等式，或称为广义的Ward-Takahashi恒等式；从Slavnov-Taylor恒等式可以推导出Green函数或顶角函数所满足的一系列关系。Slavnov-Taylor恒等式要比Ward-Takahashi恒等式更普遍，前者为顶角函数生成泛函所满足的一个泛函微商恒等式，后者是三点和两点顶角所满足的恒等式，并可从前者推导出来。
等积仿射变换，又称为幺模仿射变换

可以证明，只要从两个坐标系x、y、z、t和x'、y'、z'、t'中的一个光速的等式，就可以知道从坐标x、y、z、t到坐标x'、y'、z'、t'的变换公式是线性的和齐次的；另外这个变换的行列式等于1。如果x、y、z、t满足光速的方程，则它们经过变换而得到的x'、y'、z'、t'也满足光速方程；这种变换叫做洛仑兹变换。

我们先来讨论当点沿着Ox轴运动的最简单的情形，为了方便起见我们令光速c=1。我们把x和t看做平面上的直角坐标，即我们从几何上来考虑问题，并且我们认为洛仑兹变换L是平面Oxt的仿射变换的公式；则这个变换把一对相交的直线x±t=0变成自己。因此，变换L是沿着这两条直线作具有相同系数的压缩和伸展的联合。我们再讨论当点在平面Oxy上运动的情形，光速公式是在平面Oxy上的运动的洛仑兹公式。我们把x、y、t看做普通三维空间中点的笛卡儿直角坐标，并且把洛仑兹变换看做这个空间的仿射变换的公式；则光速公式表示一个顶角是90度的正圆锥K。从洛仑兹变换的这个几何解释看来，平面上的运动不是别的，正是这个空间的把锥面K变成自己的所有不改变体积的等积仿射变换。

我们看到，洛仑兹变换的理论、射影几何和透视理论，以及欧几里德几何，都彼此有着紧密的联系；与它们在很多方面有联系的还有复变函数论里所谓的保角变换。众所周知，在欧氏几何中，面积是用距离定义的，这种定义不能直接应用到仿射几何中来，这是因为距离这个概念在仿射几何里是没有定义的，但是，在数学分析中，面积是用积分定义的，积分的定义与直角坐标x、y有关，是依赖于长度和垂直等概念的，当然也不能直接应用于仿射几何之中，然而值得注意的是积分∫∫F(x,y)dxdy的严格定义是纯解析的，完全不依赖于直角坐标x和y，而且运算规律和通常一致。如果D是仿射平面Oxt的一个区域，那么在一般的仿射变换下D的面积不是不变的，可是对于Jacobi行列式Δ=±1的那些仿射变换，面积却是不变的，称为幺模仿射变换或等积仿射变换，幺模仿射变换的全体构成一个群，这个群和它所对应的几何都是幺模仿射的，不难证明幺模仿射变换下的面积元是一种特殊的外微分形式。

让我们来讨论某些这种特殊的洛仑兹变换。1、明显地，空间作为刚体绕锥面K的轴转一个角ω的任何简单的旋转，是空间的把锥面K变成自己的等积仿射变换，即是一些特殊的洛仑兹变换。2、空间对通过锥面K的轴的任何平面的反射π，显然也是这种洛仑兹变换。3、最后，让我们看一下以下的变换；设v和w是锥面K的某一对对面的母线，P和Q是沿这两条母线与锥面相切的平面；这两个平面互相垂直。我们作空间向着平面P的压缩和它背着平面Q而具有同一个系数的伸展，或者反之。例如我们把空间向着平面P压缩到三分之一，然后背着平面Q把它伸展到三倍。这种空间变换L显然是仿射变换而且是保留所有体积的大小的；这个变换把锥面K变成自己。由于锥面以t轴作为旋转轴，总可以把整个图形旋转到使母线v和w处在例如平面Sxt上。

我们使平行于平面Sxt的任意平面R与锥面K相交；这个平面有方程y=b，这里b是常数。把这个值代入锥面K的方程，可以得到一个双曲线的方程，对于它说，平面R与平面P和Q的交线正是渐近线；刻划这个双曲线的点是：它到渐近线，即到平面P和Q的距离p和q的乘积是常数，在变换L下，这种双曲线上的每一个点都留在同一条双曲线上，因而双曲线就变成了自己，但是整个锥面K就由这种双曲线组成，所以在空间变换L下锥面K变成了自己；因此这个变换L也是洛仑兹变换。

因为在仿射变换下直线变成直线，而且相交直线变成相交直线，所以直线丛S在任何洛仑兹变换下一对一的变成自己；此外，因为在空间的仿射变换下每一个平面都变成一个平面，所以在丛S到自己的这种变换下得到的是这个丛的射影变换，如果用一个垂直于锥面K的轴的平面Π与这个丛相交，而且认为这个平面完全不参与空间的所说洛仑兹变换，再把这个平面增补为射影平面Π*，来考虑丛S的直线与平面Π*的交点，则变换丛S的洛仑兹变换，顺带给出平面Π*的一个射影变换Λ，它把由平面Π*与锥面K的内部相交而成的圆形α变成自己。为了研究洛仑兹变换的性质，最简单的是考虑它的所谓把圆α变成自己的射影变换Λ。

量子细胞引力论

由于量子细胞引力耦合常数是无量纲的，就为重正化铺平了道路。我们现在已经知道了引力子的构造，由点线对偶性生成一个自旋为1的规范玻色子，这差不多就是普通的光子；由伸缩对偶性生成一个自旋为1的需要重整化的规范玻色子，引力子是由这两个自旋为1的规范玻色子合成出来的自旋为2的玻色子。所以传递作用力的规范玻色子都是由普通的光子加上一些佐料构成的，至少在量子细胞场论中是如此。可以看出，量子场论中那些“脑筋不正常的过程”正是量子细胞引力论的起点，不过到了射影空间变得“脑筋正常”了而已。沿着量子场论的思路就可以证明量子细胞引力论是局部可重正化的。

我们将自旋为0的引力子称为牛顿引力子，自旋为2的引力子称为爱因斯坦引力子；下图是引力子的样子：

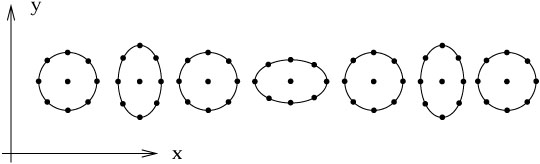
从量子场论和广义相对论的几个方面都会导致引力常数无量纲的结果；沿着Dirac的思路，当Dirac尝试推导相对论量子力学时采用虚拟开根号的方法，微分算符的一阶条件导致Dirac算子是能量算符的平方根；另外引力场的Hilbert作用量中包含度规行列式的平方根算符，直接对这个平方根算符展开会在作用量基本方程中得到一个引力子的无穷展开级数，这相当于一个无限的引力子自作用序列，而量子色动力学的Yang-Mills场的基本方程中关于胶子的展开级数除了包含三胶子自作用和四胶子自作用顶点外不包含更高阶的胶子自作用顶点。

这样就将质量有关项吸收进了质量荷中，相当于在引力作用量基本方程引入了一个截断，现在引力子的自作用也只包含三引力子顶点或四引力子自作用顶点而不包含更高的自作用项；另外，我们知道正交标架场相当于度规算符的平方根，所以引力耦合常数无量纲其实有几个方面的意义，现在引力场和Yang-Mills场有了完全一样的场方程式。对于宇宙而言，有质量物质和引力子都被封闭在一个马德西特袋中，量子细胞引力场有渐近自由的性质；这很像量子色动力学中夸克和胶子都被封闭在重子口袋里，所以有渐近自由的性质；所以可以得出结论，双重椭圆几何加双曲几何可以得到渐近自由的性质；问题是黑洞遵守的是单重椭圆几何性质，毕竟重子不会胡乱地发射胶子，而黑洞可以发射引力子，如果黑洞中的引力也有渐近自由性质，则自然可以避免奇点的产生，但如果黑洞中的引力没有渐近自由的性质，就要想别的办法避免奇点的产生了。

当然我们不能对耦合常数无量纲太迷信，现代物理实验证实所谓跑动耦合常数其实是与能标有关系的，我想无量纲耦合常数最大的好处是我们能将大自然四种基本力的场方程用一个极其简单的统一拉格朗日量写出来，即自由拉格朗日量加上一个耦合拉格朗日项；而且我们发现了大自然的另一处自相似性，即宇宙和核子之间存在着相似性，这样我们就以非常直观的方式给出了渐近自由的一个解释，而不需要一大堆繁杂的数学。

考虑两个有质量粒子通过交换引力子产生引力，沿着有质量粒子作一个无穷小的圆，根据复变函数的留数定理沿着圆积分会给出一个不变量，同时，两个有质量粒子的无穷小圆相交于两个无穷远的虚圆点，连接两个虚圆点有一条无穷远的公共弦，我们认出这两个虚圆点有点类似于产生电磁力的正电荷与负电荷；也许引力与电磁力还有更深层次上的对偶关系，不过我们现在不想深究这种类马德西纳似的关系；重要的是，正的引力电荷与负的引力电荷会使两个有质量粒子产生极化，两个有质量粒子变得像是电磁场中的偶极子，于是引力便产生了；但引力偶极子与电磁偶极子有一个重要差别，引力偶极子不会产生偶极辐射，考虑迈克尔乔丹飞身跃起扣篮，地球会向相反的方向运动从而抵消这种冲量，所以引力只会引进四极辐射；产生这种现象的微观原因是：局部的引力保持一对对合点不变，属于单重椭圆几何，需要将对径点等同起来认为是同一点，所以引力波在转过了180度后波函数保持不变。

虚的正负引力电荷产生的场是对称的，怎么会产生一个马德西特式的宇宙呢，原因主要有两个方面：一是这种对称性是非常不稳定的，像是立在桌子上的一支筷子，总要倒下来导致对称性破缺；二是按照现代宇宙论的观点宇宙一定是一个没有边界的四维流形，自然是封闭的，所以也自然会产生引力的一个取向。引力场有很强的整体效应，会产生一个整体的背景场，但这种背景场不是量子场论中那种从虚无的真空中产生出的背景场；所以牛顿引力子实际上包含两种成份：一种是导致牛顿引力势的自旋为0的分量，一种是由于量子场论中所谓的真空自发性破缺产生的一个Goldstone玻色子；但要记住，量子细胞场论中没有一个所谓无穷大的真空态。

相对论的绝对时空观

1908年9月，赫尔曼.闵可夫斯基通过与毕达哥拉斯公式的类比，发现了他的绝对时空。你可能记得，闵可夫斯基就是在爱因斯坦读书时叫他懒狗的那位数学教授。1902年，俄国出身的闵可夫斯基离开了爱因斯坦的母校苏黎世ETH，到享有国际声誉的德国哥廷根任教。在哥廷根，闵可夫斯基研究了爱因斯坦关于狭义相对论的论文，印象很深，这引导他发现了四维时空的绝对性质。

爱因斯坦听说闵可夫斯基的发现时，并不在意。闵可夫斯基只是用一种新的更数学化的语言重写了狭义相对论的定律，而对于爱因斯坦来说，数学掩盖了定律背后的物理意义。因为闵可夫斯基不断宣扬他的绝对时空观如何美妙，爱因斯坦开始笑话哥廷根的数学家。事实上，笑话落到了爱因斯坦自己身上。在4年后的1912年，为了在狭义相对论中纳入引力，爱因斯坦妥协了，闵可夫斯基的绝对时空观成了广义相对论的根本基础；遗憾的是，闵可夫斯基没能活着看到这一点，1909年，他死于阑尾炎，终年45岁。

爱因斯坦的数学功底显然不如Hilbert，爱因斯坦不是第一个发现卷曲定律的正确形式的人，第一个发现者是Hilbert；1915年，Hilbert没有走爱因斯坦那条艰难的试错路线，而是走的一条优美而简捷的看似“神学”的数学道路，推导出Einstein-Hilbert作用量，比爱因斯坦在柏林向普鲁士科学院报告相同定律早5天。爱因斯坦用的是张量分析，用陈省身的话说，从现代微分几何的观点来看，张量分析弊多利少，但张量分析简单明了，在初等问题上的功用是不可磨灭的。不幸的是，量子场论的基础也是闵可夫斯基的绝对时空观，可能虽然Klein很支持爱因斯坦，但爱因斯坦对klein的爱尔朗根纲领并不熟悉，所以没有找到相对时空观的正确表述形式，所以从量子场论和广义相对论的绝对时空观过渡到量子细胞场论的相对时空观，不仅在逻辑上而且在历史上都是必然的。当然我们用庞加莱模型和Klein的爱尔朗根纲领来统一规范场和引力场隐含了一个假设，即引力场是最大对称化的，由于目前所有关于引力的验证事实都隐含了最大对称化条件，所以这种假设也是合理的；用广义相对论的话说，量子细胞引力论与广义相对论在弱等效原理下是等价的，但广义相对论的强等效原理并未经过实验证实。

终于统一了?

有了前面这些基础知识的铺垫，我们现在可以将四种基本力统一起来考虑了。关于夸克禁闭这在量子细胞场论中有个超级简单的解释，由于强力属于多细胞生物，所以单独的细胞也就是夸克不能构成生命，当然我们不能将这种解释看得太认真，我们需要严格的逻辑推理，否则本文应该改称“大话统一场论”了；况且除了夸克禁闭外，量子细胞场论还要解决大量的其它实际问题。维尔茨克说今天量子色动力学理论在原子核实际问题中的角色，基本上同“圣水”差不多，哈罗德•弗里茨写道：“讽刺的是，QCD理论没有提供多少有关强相互作用的内容，而这正是我们研究的最初动机。”下面我们会看到，量子细胞场论大大改善了量子场论在核子相互作用中的看法。

化学键能为我们提供一些线索。氖是一种惰性气体，每个原子都是一个不发生相互作用、不带电荷的近乎完美的球体，但当两个原子相互靠近的时候，每个原子所带的电子云相对于原子核都发生了微小的偏移，结果每个原子都会呈现一点儿电极性，因此距离很近的两个原子之间存在吸引力，这就是范德瓦尔斯力。

量子细胞场论确实能为我们提供理解原子核力的基础。引力与强力都是多细胞的量子生命形式，所以两者之间有很多相似性；可以设想，夸克生存在一个正曲率的紧致无边的四维流形中，这正是黎曼几何的基本假设，所以我们这样假设也是合理的，重要的是，这个无边的四维紧致流形构成了胶子世界的边界；要记住胶子都是些虚粒子，它们的能量是借来的，既然是借来的就一定要还的，所以胶子的测地线自然终止于夸克；胶子生存在一个庞加莱双曲几何空间里，胶子是严格无质量的，所以即使庞加莱双曲几何的边界为无穷远，胶子还是能够到达边界的。我们看到，重子确实是一种口袋的形状，这是夸克禁闭的第一条线索。

同引力场一样，夸克场服从单重椭圆几何定律，而核子本身却是一个服从双重椭圆几何模型的客体，虽然我们没有黑洞与宇宙满足对偶性的证据，强力场却明显地满足单重椭圆几何与双重椭圆几何的对偶性，这已经被大量的高能加速器实验所证实。主要原因是核子的自旋是1/2，在量子细胞场论中，自旋为1/2就意谓着一定有一对对偶的场在相互转化；由于在量子细胞场论中标量粒子与矢量粒子是对偶的，所以我们只考虑标量粒子，在量子细胞场论中有两种标量粒子：一种是携带色力势的标量粒子，我们称之为色库仑子，一种是传说中的Goldstone玻色子；但量子细胞场论中没有真空自发性破缺之说，所谓Goldstone玻色子也是狭义相对论本身导出的，所以声子也与量子场论的声子有很大的不同；我们必须为量子细胞场论中的声子起一个新的名字，比如说哼哈子(Henghaon)，当然我们推荐的名称是行者或者输运子(Travellon)；之所以起这样的名字是因为它们在量子色动力学中的表兄弟瞬子可以起到在不同维空间的量子隧道中穿越的作用。

行者虽然不是真空自发性破缺所产生的，但与凝聚却有关系，负责将能量输送到双重椭圆几何的对径点上；就好像我们从地球的北极运送物质到地球的南极，北极与南极之间的测地线不存在，但我们可以选任何一条路径，但量子力学就不同了，由于没有测地线，行者一定是经过所有的路径到达对径点；这样就会与所有的夸克发生相互作用。由于存在这种单重椭圆几何与双重椭圆几何的对偶关系，所以核力的同位旋对称性实际上是这种对偶关系引起的相互作用，用量子色动力学的话说，是色力的剩余相互作用。

不管是色库仑子还是行者都起着将对径点叠合起来的作用，只是前者是对合关系，后者是输运关系，这就要求介子一定是由一个正夸克和一个反夸克组成的无色的粒子。关于夸克禁闭还有一种更强的约束，我们知道重子是由三个夸克组成的，盖尔曼先生很可能是童话小说看多了，叫了三声夸克，便虚构出了夸克这种数学对象，但夸克很可能并不对应于任何真实的物理粒子，就好像费曼的鬼粒子并不对应真实的物理粒子一样。射影空间中有一种自配极三角形，由于是自配极的，所以也满足点线对偶性，从而与行者是兼容的；重要的是，自配级三角形的面积在幺模仿射变换下是一个不变量，所以是与狭义相对论兼容的；更重要的是，假设夸克位于自配极三角形的三个顶点上，自配极三角形的面积解释为荷的话，荷是一个整数，不会出现每个夸克带1/3电荷这种奇怪的事，所以也没有自由夸克的说法。量子场论通过高能加速器击碎原子试图发现自由夸克的方法，这种试验方法是值得推崇的，但量子场论的逻辑推理是有问题的；这就好像将一辆汽车经过粉碎机粉碎成无数块惨不忍睹的碎片，然后每个碎片又会自动还原成一辆完整的汽车；一句话，QCD是还原论的，量子细胞场论是整体论的。

其实我们一直都小心翼翼的，避免与量子场论有太多矛盾的地方，我们还是有了一个容纳了大自然四种基本力的统一的几何模型，与量子场论的兼容性很好，而且比量子场论更简单也更能贴近实验事实；量子细胞场论没有困扰量子场论的所谓强CP破缺问题，没有轴矢量流的三角形反常问题。由规范势导出的标量粒子满足单重椭圆几何，与矢量粒子合在一起后就变成了极矢量；行者是动态的并且满足双重椭圆几何，与矢量粒子合在一起后就变成了轴矢量。当我们要求将对径点叠合后，电弱力的两个对合点上分别是电子和中微子，所以对于弱相互作用宇称是不守恒的；核力的两个对合点上分别是中子和质子，我们看到，强力中所谓的轴矢量流部分守恒在量子细胞场论中是这样解释的，强力并不破坏宇称的手征对称性。

为什么是量子细胞?

由于量子场论中的费米子和玻色子都是没有质量的，玻色子没有质量是因为规范不变性的要求，而费米子没有质量是因为手征性的问题，Goldstone玻色子在量子场论起到了中心作用，事实上，通过与量子细胞场论的对比我们下面将看到，通过Goldstone玻色子获取质量确实可以称为量子场论的中心法则。量子细胞场论继承了庞加莱和Klein的思想建立了与量子场论同构的一套几何理论，这套理论的基础是自同构群或自守函数，这也就意谓着空间不是连续的(但至少是稠密的)，甚至可以夸张的说，每两点之间的距离都是无穷远，这就要求所有的粒子都没有质量，因为只有无质量的粒子才能在无穷远之间穿越。量子场论采用蛮力的方法解决这个问题，即所谓的狄拉克δ函数，但δ函数本身的定义就是无穷大，这也是量子场论中令人头痛的无穷大产生的根源。

由于规范场论是局域性的，量子场论需要有一个全局性的对称性再让它破缺来平衡局部的状态变化，这就意谓着量子场论必须有一个无穷大的真空，我们的理论称为量子细胞场论，但其实我们只借用了分子生物学的中心法则，因为生物是个耗散系统，对称性是破缺的，这点与量子场论倒是很像，生命与供养它们的食物之间是不对称的，所以非洲大草原上的角马需要不断迁移来寻找食物，而量子细胞场论的细胞与对偶细胞之间的对称性是没有破缺的，从而不需要一个无穷大的真空。

局部和全局对称性之间的平衡到了理解强相互作用阶段变得迫切起来，原因在于产生和湮灭算符的作用，核子里聚集了大量的虚夸克和软夸克；直接应用产生算符会生成一个半群，例如重正化群就是一个半群，群的每个元素都有一个逆元；而半群的元素却没有逆元，在群的作用下无法回到自身；解决的办法只有一个就是引进两个全局性的函子，将半群集合的全部元素映射到另外一个半群或者反之，这两个全局性的函子在范畴论里称为self-adjunction算子，与量子力学中的self-adjoint算子有异曲同工的妙用，只是前者是针对二次量子化的而后者是针对一次量子化的；这两个整体自伴算子在分子生物学中的实例不是别的，对应的正是分子生物学的中心法则，即DNA→RNA→蛋白质的生物遗传和转录过程。

我们的行者哼哈子在量子细胞场论中起到的也是这种作用，行者哼哈子肩负的使命是将量子细胞的DNA从一点移到另外一点，DNA是没有质量的因此也是没有问题的，同时夸克也可以以无质量的方式从一点迁移到另外一点，等到了地方再根据遗传信息重组，质量就产生了，它们只是需要在传递的过程中暂时凝聚一下，并不需要整个空间中都充满了Goldstone粒子。现在回头看看量子场论简直充满了误称，真空对称性自发破缺是一个误称，所谓核力为色力的剩余相互作用也是一个误称；在量子细胞场论里，核力乃是强力的局部到全局对称性之间的平衡引发的作用力，核力的SU(2)同位旋对称性是一种全局对称性。也许等过几年量子细胞场论成熟了，我们再回头看看现在的量子细胞场论也是充满了不成熟的或者滑稽可笑的地方，但现在我们可以肯定至少在大方向上是正确的。

不仅从狭义相对论的角度，从量子力学的角度看这种局部与全局之间的对称性也是必然的，规范场的标量分量是一种局部的对称性，而行者哼哈子携带的是全局对称性产生的Noether标量流，但从量子力学的角度看，这两个标量分量必然会重合到一起，就像是两个原子通过交换电子产生共价键一样，详细的原因可以参见大牛费曼的《费曼物理学讲义》第三卷有关氨分子等篇的论述，我们这里就不再复述了。SU(2)群空间分为上下两个不连通的空间，所以弱相互作用中宇称是不守恒的；两个SU(3)群的乘积恰好同构于一个反夸克存在的反SU(3)群，这就是为什么重子总是由三个夸克组成的，强相互作用中宇称是守恒的；两个标量分量重合后描述了介子的性质，π介子是负宇称的标量粒子；量子细胞场论中没有困扰量子场论中的许多重大问题，一切都是比较完美的。

我们说两个标量分量重合，只针对椭圆几何的退化情形而言，对于引力而言显然是不重合的。在人类已经完整测序的基因序列中，有一种是线虫，这种虫子大约由一千多个细胞组成，可以认为每个线虫与其它线虫都是平凡同构的，但人太复杂了，两个人之间显然只存在非平凡同构；不过核子不比线虫更复杂，由于中子的质量是电子质量的一千多倍，可以设想核子大约由一千多个价夸克和海夸克组成，两个核子之间是平凡同构的，所以从量子细胞场论的角度我们不必恐惧强相互作用的复杂性。

胡思乱想

本小节纯属胡思乱想，再加上点胡言乱语；内容与对螺旋星系的理解有关；不过万一我们的猜想有哪一条是正确的，我们倒是有可能该准备诺贝尔奖获奖感言了。关于剩余相互作用有一点有意思的猜想，如果黑洞与我们的宇宙是对偶的关系，那么我们的宇宙在超级宇宙中也有可能扮演一个核子的角色从而与其它的宇宙发生这种剩余相互作用，只不过这些超级强相互作用也是超级的慢动作，大约交换一个超级介子的时间是几十亿年到几百亿年，至于我们的宇宙是扮演中子还是质子的角色我们就弄不清楚了。

众所周知，我们的银河系以及宇宙中众多美丽的星系都是螺旋星系；随着我们对量子细胞引力论的更深入了解，我们发现我们的宇宙变得越来越有趣了。我们隐约看到了银河系旋臂结构的一个可能的解释，众所周知银河系的中心可能存在着一个质量巨大的黑洞，这在量子细胞引力论中意谓着太阳系沿银河系公转的轨道可能不是牛顿或爱因斯坦引力论推导出来的近似椭圆的轨道，而是带着强烈的量子力学的修正；太阳系离银河系中心时而变近、时而远离，考虑到近动的影响，太阳系的轨道类似于一个一边旋转一边飞舞的蝴蝶，或者类似于一个想告诉同伴花蜜的位置而沿着8字型轨道飞舞的蜜蜂，由众多星星组成的银河系在大范围内就有可能形成旋臂结构。

经典物理图像中，唯一与动态螺旋结构相似的是龙卷风或者经由下水管排出的水形成的旋涡；我们知道，黑洞形成的引力场类似于一个漏斗的形状，如果你有幸能够到达黑洞视界的边上，你看到的天空不会是满天的星星，而是所有的星星都集中于你头顶的上方；太阳带着太阳系里的众多成员以每秒近三百公里的速度沿银河系中心公转，需要银河系里至少有三千亿颗恒星才能产生如此强大的引力场，而我们观察到的恒星大约只有一千亿颗，如果剩余的质量全部都是大黑洞携带的话，可想而知这个黑洞有多大了。如果众多星星都是冲向大黑洞的话，就会很自然地形成螺旋结构，但这样会带来一个问题，众多星星这样排着队、视死如归地踏上一条不归路，不仅与观测事实不符，在感情上也接受不了，毕竟银河系大约已经存在了一百多亿年了。

似乎有一种很硬的背景一直提升着冲向大黑洞的星星，当星星离得与大黑洞较近时轨道便被反弹了回去，于是便形成了我们所说的蝴蝶型的轨道。这种很硬的背景很可能与自旋有关，大黑洞可能带有强烈的自旋，但这种自旋不是广义相对论中的Kerr黑洞的自旋而是量子世界的自旋；在量子世界里所有的粒子都带有自旋，这种自旋是在内部空间里的一种自旋，所以不是Kerr黑洞的自旋。由于引力与强力有很多相似之处，借助强力我们可以理解一些引力的现象，但引力还是比强力复杂得多，爱因斯坦的广义相对论将引力场过于简单化了。

我们已经将强相互作用中的真空超导化机制排除了，这就意谓着如果量子细胞场论对强作用力的看法是对的，特Hooft等一系列大牛的看法便被否定了，不知道这些大牛们会不会向我们扔砖头:-)不过黑洞中确实应该是超导化的，在我们看来黑洞的视界温度接近绝对0度，可见黑洞内的对称性自发破缺是不可避免的，于是会产生大规模的集体激发现象，引力的Goldstone玻色子自然会出现从而引发大范围的引力自旋波。引力自旋波的效应只有当星星离大黑洞较近时才较为明显，而且按照我们的分析引发的效应应该是排斥性的，也就是借助于引力场强张量的对偶场强张量发挥作用的。另外，黑洞也会是一个超级哼哈子，哼哈子的作用在于使各个星星的轨道排列有序，就像它们在强力中扮演的角色一样；只有到我们对量子细胞引力有了更深入的了解并进行精确的计算后才能知道到底发生了什么。

中心法则

我们认出这正是规范场论赖以生存的根本大法，所以称之为中心法则也不为过。半个多世纪前，Weyl和杨振宁等人将整体对称性提升到局部对称性，规范场便自动地冒了出来；今天我们反其道而行之，将二次量子化后的局域对称性提升到整体对称性，核力的同位旋对称性便自动地冒了出来；难道这不是很美妙吗? 我们事实上已经提开了质子自旋之迷，其实在量子场论界所谓核子自旋危机这个名词已经由来已久，早就失去它应有的紧迫感；量子场论中核子失踪的自旋是哼哈玻色子携带的；那么自旋为0的哼哈子是如何携带核子的自旋呢? 答案还是与对偶性有关，在射影空间中移动一段距离和旋转一些角度是对偶的，所以标量与旋量也是对偶的，这就是量子细胞场论的好处，一旦我们知道一个命题是成立的，那么它的对偶命题便自动成立。

通过与细胞物理学的类比，我们可以分析出量子场论的中心法则遗漏了些什么。产生和湮灭算符是一对自伴的算符，与DNA→RNA→蛋白质的细胞生物学的中心法则确实是相似的；但直接应用这个规则生成的是一个递归可枚举集，这个集合里有大量的不可判定的命题，比如有个南京人说所有的南京人都说谎，这句话符合语法但导出的却是一个自相矛盾的结论，在逻辑上是没有意义的；因此在逻辑上我们只关心递归集，递归集里的语句不仅符合语法而且都是有意义的。要想让细胞递归就必须联系上细胞周期，我们知道细胞周期类似于量子场论的相位因子，规范场是一个相位因子场，没有了相位因子就没有了量子的特点，量子场论与经典力学并没有区别。

所以完整的中心法则必须联系上相位因子，这类似于细胞通过分裂自我繁殖的过程，仅有夸克的复制是不够的，必须联系上核子的DNA的复制。狭义相对论否认了真空中的以太说，量子细胞场论的看法也否认了量子场论中现代版的以太说。现在让我们看看在一个相位转过360度的周期内都发生了什么，这与量子力学的几率概念是对应的，这时量子细胞从一点迁移到时空中的下一点，我们让时空暂时破缺一下，就是从四维暂时破缺到三维，到了下一点再恢复成四维，我们认出这正是量子场论中通过轴矢量粒子获取质量的机制；所以粒子的质量便产生了，到了下一点后，量子细胞再来一个细胞分裂，让对偶细胞在下一个下一点等着量子细胞。

我们看到这种获取质量的机制是不需要真空中有大量粒子凝聚形成的背景场的，这样我们就摈弃了现代版的以太说。重要的是，这种机制与德布罗意的E=hω假说是兼容的，我们可以认为ω就是量子细胞的周期，这样我们就将量子力学与爱因斯坦的质能关系式统一了起来，我们看到量子细胞场论与狭义相对论和量子力学的基本假设确实都是兼容的；物理学经过了一个多世纪的发展，终于从终点又回到了起点，伴随着的是人类认识上的巨大进步。

微分几何与统一场论

Felix Klein在1871年阐述了埃尔朗根纲领；这就是几何学定义为研究有连续自同构群的空间，例如欧氏空间具有刚体运动群，射影空间具有射影直射变换群等。其中包括非欧几何学，根据Klein的观点，非欧几何学只要在空间中有一个所谓二次的超曲面，讨论在所有的投影变换下，使这个二次超曲面不变。例如：在平面上有一个圆周，非欧几何就是要讨论在投影变换下圆周仍不改变的性质。因此根据Klein的观点，非欧几何学就变得极易处理。

Klein的埃尔朗根纲领与狭义相对论完美地结合，狭义相对论中的一个原理是洛伦兹群下场方程的不变性，这导致了Klein这们处于世纪转折时期最有影响的德国数学家成为狭义相对论最早的支持者之一。洛伦兹结构在相对论中起了基本的作用，它还有几何学的解释。当我们研究空间中球的几何时，将球变为球的所有接触变换构成一个15参数群，而把平面变为平面的变换构成一个10参数的子群，后者与4个变量的洛伦兹群同构，所导致的几何学就是拉盖尔的球几何学。

Klein的埃尔朗根纲领的成功自然地引起了Klein空间或现在称之为齐性空间中的微分几何的研究；跟随Weyl之后产生了维布伦的相对论的射影理论，维布伦的理论是四维的，但切射影空间有五维的齐次坐标，维布伦的射影理论在几何上是简单的，他的出发点是空间的路径，它们是带电粒子的轨线；道路空间几何学涉及到射影联络。

在Klein制订埃尔朗根纲领时，已观察到黎曼几何并不包括在内，因为一个一般的黎曼空间除恒等变换外并不含有其他等长变换。Elie Cartan在他的主要论文《仿射联络的流形及广义相对论理论》中给出仿射联络的论述以及它向有挠率联络的推广；它比仿射联络论的内容更丰富；它的思想可以容易地推广到任何李群的纤维丛的联络理论中去。

用几何的话来说，仿射联络是一族仿射空间即纤维，它们由一个基底空间所参数化，使得这一族仿射空间是局部平凡的，并且有一个纤维沿着基底空间的曲线展开的法则，使线性关系得以保持。类似地，我们可以把Klein空间当作纤维并且用作用于Klein空间的李群来代替完全线性群，并且也有一个对应的展开法则；Cartan称这样的结构为一般空间。一般来说，这个联络是非和乐的，即展开依赖于基底空间的曲线。换句话说，沿一条闭曲线作展开时，空间并不回到原来的位置，它的变差是由联络的曲率来度量的；显然，Klein空间本身是一个曲率恒等于0的一般空间。从Cartan的观点来看，黎曼空间是一个以欧氏空间为纤维的空间，并且具有Levi-Civita联络；这解决了微分几何中的一个基础的问题，因为这样就有了一个概念，它包括了Klein空间、黎曼空间以及这两种空间的推广。

纤维丛与自对偶

欧氏空间只有一个切空间，现在的空间情况复杂了一些，每点都有一个切空间，但都是平坦空间；这个现象在几何上有一个重大的发展，就是把切空间竖起来；我们就叫它为纤维丛，或叫矢量空间丛。Maxwell方程就是建立在一个矢量丛上，这个纤维丛是复数空间；现在是一把复线，你如果能有法子从这个纤维到另外一个纤维有一个平行性的话，就能立刻得到Maxwell方程。现在纤维丛上有一个平行性，这个平行性的微分，等于电磁场的强度F，然后把这个F再求它的余微分的话，就得到流矢量J。用下面两个简单的式子，就把Maxwell方程写出来了，F=dA，δF=J。在电磁学里，要把Maxwell全部写出来的话，书上往往是一整页；其实简单地说，也就是平行性的微分是场的强度，而场的强度的余微分就是流矢量。

所以Maxwell方程就是建立在一个复的纤维丛上，你怎样把每个纤维拼起来呢，需要群的概念，即U(1)群，群里有一个运算，把一个纤维可以挪到其他一个纤维，这是个可交换的群，叫做Abel群。欧氏平面可以引进复坐标便成为复线，它的欧氏度量变为埃尔米特度量；所以电磁学的基础是洛伦兹流形上的埃尔米特线丛。电磁学的概念可以推广到高维的复矢量空间丛和埃尔米特空间丛。杨振宁先生用到一个非Abel群SU(2)群。用SU(2)联络，把同样的方程写出来，就是Yang-Mills方程，F=dA，δF=J。

在物理上有一个Bohm-Aharonov实验，就是说：电磁学中的Maxwell方程写成那样的形式是不对的，因为它没有把所有的电磁现象都表示出来，应该利用圆周丛联络A，F=dA才是描写所有电磁现象的方程式。Bohm-Aharonov实验是这样的，有一个内有磁场的圆筒，外面没有磁场，而在圆筒的外围接有线圈，那么圆筒内的磁场，便和通电的路径有关。

人们发现，这些微分几何概念很可能是统一场论的数学基础；研究同位旋时，Yang-Mills所用的本质上是SU(2)丛的一个联络，从联络可以定义作用量。四维欧氏空间上的SU(2)丛中使作用量取最小值的联络被称为瞬子；它的曲率有一个简单的表达式，称为自对偶关系；从而瞬子是Yang-Mills场的自对偶解。当四维欧氏空间紧致化成为一个四维球时，SU(2)丛除了一个同构外由一个拓扑量子数决定；对于给定的拓扑量子数，四维球上曲率为自对偶的联络的集合是一个称为模或参数空间的光滑流形。

阿蒂亚和Ward注意到，自对偶的Yang-Mills场可以很好地纳入彭罗斯的扭量方案。瞬子通过以下的结果表明它和爱因斯坦的关系；群SO(4)局部同构于SU(2)╳SU(2)，所以四维黎曼流形M上的黎曼度量通过投影给出一个SU(2)丛的联络。依投影的方法而区分，M为爱因斯坦流形的充要条件是这些联络为自对偶或反自对偶。我们需要指出的是，丛和联络这两个几何概念是非常简洁的，我们相信爱因斯坦会喜欢它们。
Cartan几何

广义相对论用到的是黎曼几何，黎曼几何中一个重要的事实就是，你不仅要考虑黎曼流形本身而且必须考虑流形上的纤维丛；我们的方法是，直接考虑纤维丛；而通常的张量分析方法通过强调局部坐标系来回避它。大量的几何研究都是关于那些在局部坐标变换下服从简单规律的问题；关于局部问题，Elie Cartan对此当然是很熟悉的，他为他的几何实在，仿射联络、射影联络、正则联络等等的一般理论引进了切空间的概念。Cartan意义下的切空间并不总是切向量空间，这构成了难以理解他的工作的原因之一。

我们的问题是研究微分流形上以局部坐标系形式给出的几何实在，这样的问题一般总有可能在某种意义下定义在与该流形关联的一个自然的纤维丛上。于是这个几何实在以唯一的方式在纤维丛中定义了一组线性微分形式，对于黎曼几何来说，这个自然的纤维丛就是流形上全部标架所形成的空间，而相应的微分形式给出的实际上是Levi-Civita平行；关联的纤维丛的性质由解决所谓等价问题而得到最佳的确定。

一般情况	特殊例子
纤维丛(Circular Point)	球面的切向量流形
纤维丛的点	切向量
底空间	球面
纤维	同一基点上的向量
投射	把切向量映射到其基点
纤维中的变换群	同一基点的向量空间中的仿射或旋转群

纤维丛的一个简单例子就是三维欧氏空间中所有与某一球面相切的非零向量形成的流形。这是个拓扑流形，虽然很特殊；然而结果表明，具有类似性质的流形在拓扑学在微分几何的应用中发挥了重要的作用。
物质场与黎曼几何

我们的马德西特宇宙模型对物质场而言是正常曲率的，相当于隐含了一个宇宙学常数，但这个宇宙学常数与爱因斯坦的宇宙学常数方向上是相互垂直的；这就是量子细胞引力论与广义相对论的不同之处。广义相对论将引力论过分简单化了，反而引出了很多病态的结论，正所谓欲速则不达；量子细胞引力论引入了许多现代量子场论中的概念，所得到的结论却常常是意外的简单；物质场所在的正常曲率空间的拓扑量子数是1，这符合我们原先将我们的宇宙看成是超级宇宙中的一个超级基本粒子的想法。虽然量子细胞引力论与广义相对论对黎曼几何的解释有所不同，但黎曼几何却是两套理论共同的基础，所以我们有必要先学习一下黎曼几何的知识。

Gauss在1827年的文章中，对于一个由测地线构成的三角形，证明了一条关于曲率的著名定理。设K是一个曲面的可变曲率，于是∫∫KdA是这个曲率在面积A上的积分；Gauss的定理用于这三角形时说∫∫KdA等于三个角之和减去π；这就是说，在一个测地三角形上曲率的积分等于三个角之和超过180度的盈量，或在三个角之和小于180度量，等于三个角之和不足180度的亏量；Gauss说这个定理应该算是一个最精美的定理；这个结果推广了Lambert的定理，后者断言球面三角形的面积等于它的球面盈量与半径平方之积，因为在一个球面三角形上K是常数且等于半径平方的倒数。

Riemann提出的空间的几何并不只是Gauss的微分几何的推广，他重新考虑了研究空间的整个途径。Riemann在完成了他的n维几何的一般研究，并说明如何引进曲率以后，进而考虑特定的流形，在这种流形上，有限的空间形式应当能够移动，而不改变其大小或形状，并且应当能够按任意方向旋转；这就把他引到常曲率空间。当在一点所有曲率的测度都相同，并且等于其它任何点的所有曲率的测度时，我们得到Riemann称之为常曲率的流形；在这种流形上可以讨论全等的图形。如果α是曲率的测度，常曲率流形上无穷小距离元素应作相应的改变。

对于正的常曲率α等于某个超半径a的平方，并且n=3的情形，由于Gauss的工作，可以得到一种三维的球面几何，虽然不能把它形象化；这个空间在广度上有限但是无界；在其中所有的测地线都是定长，等于2π/a，并且回到它们自身。如果不考虑时间维而只考虑三个空间维，则马德西特时空中物质场的分布基于的正是这种模型，并且我们已经自然地考虑了引力的潮汐效应；如果考虑了时空的对偶性，则很自然地可以推广到四维时空的情形。至于Riemann是否认为常数正曲率曲面上的测地线都交于一点或两点，实际上是不清楚的。

Felix Klein后来指出，这里涉及到两种不同的几何。经常，两个或者更多的不同的几何有同构的自同构群。这就产生了从爱尔兰根纲领的抽象群解读出具体的几何的问题。一个例子：可定向(也就是说，反射是除外的)椭圆几何(也就是，把n维球面相对点等同的曲面)和可定向球面几何(同样的非欧几里得几何，但是相对的点没有等同起来)有同构的自同构群，偶数n的SO(n+1)。这两个看起来不同。但是事实上，这两个几何紧密相关，以一种可以精确描述的方式。1886年，Friedrich Schur证明了一个后来以他的名字命名的定理，根据Riemann提出曲率概念的思路，Schur讲到空间的一个定向的曲率，这种定向由一束测地线μα+λβ确定，其中α和β是从一点出发的两条测地线的方向；这个束构成一个曲面并且有一个Gauss曲率，Schur称之为这个定向的Riemann曲率。他于是断言，如果空间的Riemann曲率在每一点都同定向无关，则Riemann曲率在全空间是常数；因此，这种流形是一个常曲率空间。由此可见，从Schur的想法发展到量子细胞引力论中的椭圆丛空间又是一种自然的推广。
细胞量子化

细胞量子化的线索来自于几个方面。第一条线索是对狭义相对论完备性的考查迫使我们进入射影丛的空间；第二条线索来自于规范场将主丛上联络作为基本几何量的考虑，前面我们已经说得很多了。第三条线索则直接来自于矩阵力学和正则量子化方法，正则量子化方法牵涉到对偶场量的量子化，为了从经典理论过渡到量子理论，我们必须把坐标及其共轭动量看成是作用在可能的物理态Hilbert空间中的算符，再对它们加上量子条件，这就是正则量子化方法；这些场函数遵从由拉氏量导出的微分波动方程；这样作了以后，我们就得到了Bohr互被意义下的电磁场的粒子解释。

要得到一个具有微分波动传播的理论，场函数必须是连续参数空间和时间的连续函数，场在一点的改变由无限邻近于该点的那些场的性质来决定。对于大多数经典波动场，这样的描述是个理想化，它只在距离大于表征介质颗粒大小的特征长度时成立。如果我们简单地保持这样的观念，即借助连续时空坐标的微观表述是Lorentz不变的，那么我们预期相互作用通过时空的传播速度不大于光速，这种微观因果性的概念强烈地迫使我们进入场的概念。

高能范围内狭义相对论的正确性有着肯定的证据，而且也已有肯定的证据表明，微观因果性概念是一个正确的概念。正则量子化方法有一个缺点，即时间与空间不是平权的，时间坐标带有特殊的地位，所以不太适合狭义相对论体系；当然可以用路径积分量子化方法来克服这个缺点，但路径积分量子化方法非常复杂，并且也只适用于计算高斯分布这种特殊的情形；细胞量子化方法是另一种克服这个缺点的办法，在射影对偶空间中时间和空间是平权的，而射影丛空间中恰恰有大量的对偶性存在。电磁场为细胞量子化方法提供了一个佐证，电磁场恰好是自对偶的，但这种自对偶性只对无源的自由场成立；非齐次的Maxwell方程是有源方程，对偶性被破坏了，所以我们引用了射影空间中惯用的引入无穷远元素的办法来解决这种问题，电荷变成了射影空间中的无穷远元素，补充了这个仿射补丁后，整个空间都是完备的，对偶性在空间中的每一点都严格成立。

经典场论中的对偶性

对偶性存在的第一个例子来自于经典场论；自然界中没有一个粒子严格服从Klein-Gordan方程，只有当某些对偶性存在的情况下才近似服从Klein-Gordan方程。当我们研究波导中的电磁辐射及地球电离层中的电磁波时，我们会碰到与Klein-Gordan方程一样的色散关系。中性等离子体由带有一些电离分子的中性分子气体所组成；每个一阶电离分子就是推动一个负电子的正离子。地球的电离层是一层空气，它含有许多电离的空气分子；空气分子的电离往往是由于吸收了太阳发射的紫外光量子。因为平均来说等离子体是中性的，它不能作为产生静电场的源。

可是，等离子体在任何一瞬间，可能在某一个区域电荷稍许过剩，而在相邻的另一区域电荷相应地减少，这样就在等离子体中产生电场。在电场作用下，离子沿一个方向加速，电子则沿相反方向加速。电荷运动的方向，趋向于去消灭那些产生电场的电荷的过剩或过少；于是这里有了一种恢复力。当电荷过剩的数量被抵消为0时，相应的电场也变为零，这时离子和电子已获得了速度；惯性使得它们冲过头，造成新的电荷过剩和不足，正负号与原来的相反。

在粒子的量子描述中，相对论性德布罗依波的色散关系也服从同样的方程，即Klein-Gordan方程。我们看到电荷与质量可以具有对偶关系，如果我们假设爱因斯坦的质能关系式反映的是质能对称性背后的质能对偶性，则自然就可以得到单重椭圆几何与双重椭圆几何对偶的结论，用物理学语言说就是极矢量与轴矢量对偶。我们看到，具备了这样一种对偶关系后，电磁力→弱力→强力→核力这样一种导出的链式规则便自然呈现在我们面前；电磁场中只有极矢量，不存在这种对偶关系，所以光子是没有质量的；W和Z玻色子存在这种对偶关系，便有了质量。
量子细胞场论的基本定理

量子场论中存在着大量的对偶性；虽然量子细胞场论与量子场论对一些重大问题的看法不同，在牵涉到对偶性关系上两者基本上是同构的；量子细胞场论可以以这些量子场论中已经存在的对偶关系作为登陆点，达到取其精华、去其糟粕的目的。我们看到，量子细胞场论以比量子场论简单得多的推理便获得了相同的经过实验检验的结论，并附带着解决了量子场论中许多由来已久的困惑。从这个角度来说，量子细胞场论也可以称为简化量子场论，或者称为数学家会喜欢的对偶场论，当然我们最喜欢的还是带点物理味道的量子细胞场论这个称呼。

自对偶性与彭罗斯的扭量理论有关，也与共形不变性有关；可以证明在任意的偶数维中只存在场强为自对偶的自由共形理论；在任意奇数维中自由共形理论只存在标量与旋量。这个定理说明了在量子细胞场论中为什么包括引力子在内的规范玻色子的测地线遵守的是庞加莱双曲几何模型，当且仅当在这种情况下规范场强才是自对偶的并且是共形不变的，这条定理可
...

注册或登录后查看完整内容

源地址：http://blog.renren.com/GetEntry.do?id=736261476&owner=379072738

‹上一篇：变型金刚3 要约谁去看捏？额们丹东人看了要转啊！：下一篇›

分享这篇日志的人也喜欢查看更多»

陆永熙 : 为什么无语捏？

2011-07-06 19:30

杨岩 : 你好~~请问你觉得意识是种物质吗？？

2012-11-04 14:26

原文琦 David : 回复赵永峰：话说这个研究有什么实际的意义吗……

2012-07-11 01:12

赵永峰 : 回复原文琦 David:这是描相互作用的最最最基础的理论啊……

2012-07-11 01:15

原文琦 David : 回复赵永峰：嗯……我表示我的物理完全停留在高中水平了……真的搞不懂这个了……

2012-07-11 01:18

赵永峰 : 回复原文琦 David:其实就是找到一个可以描述微观引力现象的理论……大概……

2012-07-11 01:19

原文琦 David : 回复赵永峰：哦……很久不学物理了……真是……估计现在太难的高中物理题也不一定可以搞定了……我觉得现在脑子就装得下那些适应征，禁忌征和诊断标准治疗原则之类的了……哈哈

2012-07-11 01:24

赵永峰 : 回复原文琦 David:囧……职业化了……

2012-07-11 01:26

原文琦 David : 回复赵永峰：嗯……实习么……现在手里还管了两个病人……搞得我天天查房时特别紧张，老师总喜欢在不经意间问我问题……有时我本来只是向老师确认病历上的一个诊断，结果老师却又问我你认为这个诊断是如何做出的……唉……所以回去赶紧看书啊……画了一周把心脏内科常见病全复习了一遍，还是难以对付老师的提问……今天还有给我讲了一堆，让我回去好好看书，说周四还要问我，看我记住了木有……

2012-07-11 01:31

赵永峰 : 回复原文琦 David:的确好辛苦……加油做吧，也没什么别的办法了……

2012-07-11 01:52

原文琦 David : 回复赵永峰：嗯～你也加油！

2012-07-11 01:52