神秘天体黑洞“奇点”无穷大- 星球探索- 星球日报网 ...
www.planetsdaily.com/show-7-13063-1.html
轉為繁體網頁
轉為繁體網頁
天体力学定性理论_百度百科
baike.baidu.com/view/774991.htm
轉為繁體網頁
轉為繁體網頁
第二节复数的几何表示
fbhs.snnu.edu.cn/kcwz/all/dianzijiaoan/1/12.ppt - 轉為繁體網頁
檔案類型: Microsoft Powerpoint - 快速檢視我们可以用球面上的点来表示复数. 我们规定: 复数中有一个唯一的“无穷大”与复平面上的无穷远点相对应, 记作. 因而球面上的北极N 就是复数无穷大的几何表示.
0Comment count
|
107View count
|
3/2/14
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0Comment count
|
4View count
|
2/24/14
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0Comment count
|
100View count
|
2/24/14
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
brain01 全同粒子 diffgeom01 expecations 从很多方面蚂蚁都可以感知三维世界. 触角是三维的; ,如果在每个局部坐标系 U 里有一组数据,当一个区域可以使用不同局部坐标 U, U’,而 U 里头的数据可以通过某种(依赖于局部坐标变换的)规则同 U’ 里的数据联系起来的时候,这组数据就组成了一个整体定义的量。这跟狭义相对论还是有所不同,在那里,时空是平直的,坐标系之间的变换同空间本身的 Poincare 群作用几乎可以对等,所以教材上面从来不区分是“坐标变换” 还是“点变换”。在流形上,坐标都是局部的,这种区别就很关键了。
相对论与黎曼几何-12-双生子佯谬
|||
12. 双生子佯谬
爱因斯坦幸运地结交了两位犹太人数学家朋友:闵可夫斯基和格罗斯曼。
一开始,爱因斯坦对闵可夫斯基的四维时空不以为然,但当他结合黎曼几何考虑广义相对论的数学模型时,才认识到这个相对论少不了的数学概念的重要性。
尽管物理学家企图将时间和空间统一在一起,但两者物理意义上终有区别,无法将它们完全一视同仁,一定的场合下还必须严格加以区分。于是,天才数学家庞加莱将四维时空中的时间维和空间维分别用实数和虚数来表示。也就是说,将时空用3个实数坐标代表空间和1个虚数坐标描述时间。或者是反过来:用一个实数坐标表示时间和3个虚数坐标表示空间。到底是让空间作为实数唱主角(前者),还是像后面一种情况那样将时间表示为实数,只不过是一种约定或习惯而已。后一种表示方法是本系列文章中将经常使用的。 后来,闵可夫斯基发展了庞加莱的想法,他用仿射空间来定义4维时空。如此一来,就可以在形式上用对称而统一的方式来处理时间和空间。类似于3维欧几里德空间中的坐标旋转,洛伦茨变换成为这个4维时空中的一个双曲旋转。在欧几里德空间中,两个相邻点之间间隔的平方是一个正定二次式: ds2 = dx2 + dy2 +dz2, 但这点不适用于闵可夫斯基时空,理由很简单,因为时空中的坐标除了实数之外,还有了虚数。根据刚才的约定,闵可夫斯基时空中两个相邻点之间间隔的平方变成了: dt2 =dt2 - dx2 - dy2 - dz2, 这儿的dt被称为固有时。不同于欧几里德度规,闵可夫斯基时空的度规是“非正定”的。这种非正定性也导致闵氏空间具有了许多不同于欧氏空间的有趣性质。 从物理的角度,时间和空间的最根本不同是时间概念的单向性。你在空间中可以上下左右四面八方随意移动,朝一个方向前进之后可以后退再走回来。但时间却不一样了,它只能向前,不会倒流,否则便会破环因果律,产生许多不合实际情况的荒谬结论。
爱因斯坦的狭义相对论将时间和空间统一起来,彻底改变了经典的时空观,由此也产生了许多“佯谬”,双生子佯谬是其中最著名的一个。
根据相对论,对静止的观测者来说,运动物体的时钟会变慢。而相对论又认为运动是相对的。那么,有人就感到糊涂了:站在地面上的人认为火车上的人的钟更慢,坐在火车上的人认为地面上的人的钟更慢,到底是谁的钟快谁的钟慢啊?之所以问这种问题,说明人们在潜意识中仍然认为时间是“绝对”的。尽管爱因斯坦先生将同时性的概念解释得头头是道,听起来也似乎有他的道理,但是人们总觉得有问题想不通,于是,便总结出来了一个双生子佯谬。最早是由朗之万在1911年提出的。
话说地球上某年某月某日,假设在1997年吧,诞生了一对双胞胎,其中哥哥(刘天)被抱到宇宙飞船送上太空,另一人(弟弟刘地)则留守地球过普通人的日子。宇宙飞船以极快的速度(光速的四分之三)飞行。根据相对论的计算结果,在如此高的速度下,时间变慢的效应很明显,大概是3比2左右。所谓“时钟变慢”,是一种物理效应,不仅仅是时钟,而是所有与时间有关的过程,诸如植物生长、细胞分裂、原子震荡,还有你的心跳,所有的过程都放慢了脚步。总之就是说,当自认为是在“静止”参考系中的人过了3年时,运动的人却只过了2年。按照地球人的计划,1997年发射的那艘宇宙飞船,将于30年之后掉头反向以同样的速度飞回地球。因此,总共经过地球上60年之后,2057年,一对双胞胎能够再见面啦!那时候,地球上的弟弟刘地已经60岁了,但一直生活在高速运动的飞船中的哥哥刘天却只过了40个年头,人到壮年,风华正茂的年月。不过,有人便说:刘天会怎么想呢?爱因斯坦的狭义相对论不是说所有的参考系都是同等的吗?刘天在飞船中一直是静止的,地球上的弟弟却总是相对于他作高速运动,因此,他以为弟弟应该比他还年轻许多才对。但是,事实却不是这样,他看到的弟弟已经是两鬓斑白、老态初现,这便似乎构成了佯谬。无论如何,我们应该如何解释刘天心中的疑惑呢?
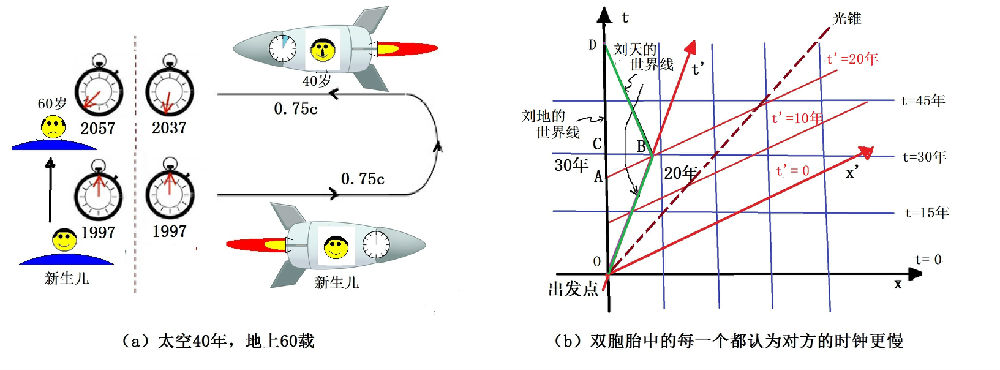
图2-12-1:双生子佯谬和同时性
首先,刘天有关狭义相对论的说法是错误的。狭义相对论并不认为所有的参考系都等同,而是认为只是惯性参考系才是等同的。刘天所在的宇宙飞船的飞行过程分成了飞离地球和飞向地球这两个阶段,每一段过程相对于地球而言都是作匀速运动,都能够分别当作是惯性参考系,但整个过程却不能在一起作为一个统一的惯性参考系。既然出发又再回头的宇宙飞船对整个过程而言并不是一个惯性参考系,刘天便不能以此而得出刘地比他年轻的结论,因而“佯谬”不成立。当刘天返回地球时,的确会发现地球上的弟弟已经比自己老了20岁。如果设想宇宙飞船的速度更快一些,快到接近光速的话,当它再次返回地球时,的确就有可能出现神话故事中描述的“山中方一日,世上已千年”的奇迹了。
我们可以使用刚才介绍的闵可夫斯基时空,更为仔细地分析这个问题。不过,我们并不需要画出4维的图形,只需要像图2-12-1b所示的,画出一个时间轴t加一个空间轴x,就足以说明问题了。
图2-12-1b中用黑线标示的直角坐标系(t,x)是地球参考系中的坐标。在这个坐标系中,两个双生子的时空过程,可以分别用他们的“世界线”来表示。什么是世界线呢?就是某个事件在时空中所走的路径。用这个新名词,以区别于仅仅是空间的“轨迹”或者仅仅时间的流逝。比如说,刘地在地球上一直没有动,所以他的世界线是沿着t轴,从出发点O->A ->C->D,图中是一条垂直向上的直线。而宇宙飞船中的刘天的世界线在图中是从O ->B ->D的一条折线。
也就是说,两个双生子的世界线都是从O到D,这是标志他们交汇见面的两个时空点:分别对应于出生时(O)和地球上60年之后(D)。两人的世界线中的一条是直线,一条是折线,这又说明什么问题呢?读者可能会认为:折线不是比直线要长吗?这点在普通空间是正确的,在“时空”中却未必见得,那是因为在这个2维时空中的距离平方:
dt2=dt2-dx2 (2-12-1)
的原因,而在普通2维坐标空间中:
ds2=dx2+dy2 (2-12-2)。
公式(2-12-1)中时空度规中的负号造成了时空空间的一些奇特性质。
首先,我们用图2-12-1b,观察解释一下时空中同时概念的相对性。对地球参考系(黑线直角坐标)而言,同时的点位于平行于x轴的同一条水平线上。比如说,地球上2012年发生的事件都在标志了“t=15年”的那条水平线上。这段时间内,宇宙飞船相对于地球作匀速运动,可以看作是一个惯性参考系。飞船参考系的坐标相对于地球参考系的坐标来说有一个旋转,如图中红色的斜线所表示。读者务必注意,这儿的所谓“坐标轴旋转”,也不同于普通空间中的旋转,被称之为“双曲旋转”,因为在闵可夫斯基时空中坐标变黄时需要保持光速不变,所以,当时间轴顺时针转动时,空间轴需要逆时针转动。在刘天的飞船参考系中看起来,平行于x’的红色斜线才是等时线。比如说,可以看看图中的A、B、C这三个事件。地球上的刘地看来,C和B是同时发生的,都发生在地球上的2027年,C点对应于自己30岁了。在宇宙飞船上的哥哥刘天呢,本来也应该是30岁,但是他的飞船时间过得慢,所以,哥哥只有20岁。飞船上的刘天怎么说呢?他不认为C和B是同时的。按照他的红线坐标,B和A才是同时的,B点对应于自己20岁,与B同时的是A点,弟弟相对于我,是运动的,时间应该更慢,所以,他还不到20岁。
在图中的这两个坐标系中(黑色和红色的),两个人的说法都是正确的,每一个人都观察到对方坐标系中的时钟比自己的更慢,从而都可以得出对方比自己更年轻的结论。但是,处于这样两个相互作匀速直线运动参考系中的双胞胎,出生且相互分离之后便永远不可能再见面,因而也就不可能构成前面所述的佯谬。不过,读者可能会说:他们虽然不能见面,但是可以通电话呀,在电话中他们互相一问,不就知道对方多少岁了么?然而,狭义相对论认为信息的速度不可能超过光速,当他们以光速通话时,也需要考虑他们之间的距离以及同时性的问题,对此我们就不进一步分析了。
在我们的故事中,地球上过了30年之后,太空船掉头向地球飞来,但这时的飞船参考系,已经不同于原来红线坐标的那一个了。要使太空船掉头达到反方向的速度,加速和减速的过程是必不可少的。在这个过程中的刘天感觉将如何?是不是被压扁或撕裂了啊?还能那么年轻力壮吗?我们且不去考虑这些种种问题,仅仅从狭义相对论时钟变慢的效应来估算他的年龄而已。
那么,既然在双生子佯谬中需要考虑宇宙飞船的加速度,是不是需要广义相对论的知识才能解释清楚它呢?也不是这样的。用地球参考系的2维时空图就可以解释清楚了。这儿,首先需要介绍一下在相对论中很重要的“固有时”概念。
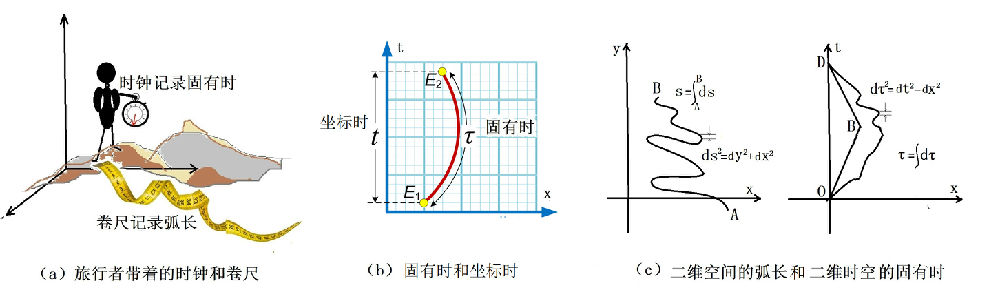
图2-12-2:固有时和坐标时的区别以及与弧长的类比
固有时,或称原时,也就是公式(2-12-1)中的t,在(2-12-1)中表示的是微分形式的dt,一段有限长度的固有时可用积分来计算得到。将公式(2-12-1)和(2-12-2)比较一下可知,固有时t类似于普通空间中弧长s的概念。在普通空间中,弧长s表示一条曲线的长度,或者说是一个人走过的路径的长度。设想如图2-12-2a的旅行者(太空人),带着自己的时钟和卷尺(计步机),一直记录他走过的距离和时间。他的计步机(或卷尺)计算测量他走过的距离,而他的时钟所记录的,就是固有时,见图2-12-2c。从图2-12-2b可以看出固有时和坐标时的区别,坐标时是事件之外的观察者使用某个参考系而记录的事件发生的时间,固有时则是旅行者自己携带的时钟记录的时间。此外,固有时与弧长不同之处是:普通空间的弧长一般比坐标数值更大,但固有时却比坐标时更小,其原因从公式(2-12-1)中显而易见,正是因为度规中空间坐标和时间坐标间的符号差。换言之,固有时用以描述时空中两个事件之间流过的时间,这个时间被赋予事件自身的时钟所测量。因而,测量结果不仅取决于两个事件对应的时空点位置,而且也取决于时钟参与其中的具体过程。再表达得更简要一点,固有时是时钟的世界线长度。
实际上,我们之前学过了黎曼几何,对固有时的概念不难理解,它就是对应于在黎曼几何中经常强调的内蕴几何不变量:弧长s。对广义相对论重要的内蕴性质,在狭义相对论中也很重要。
如何来计算两个双胞胎在重逢时各自度过的真实年龄呢?结论是:计算和比较他们在两次相遇之间的固有时。因为固有时t是内蕴不变的,这个计算可以在任何一个参考系中进行,都将得到同样的结果。每个人的年龄是由他身体的新陈代谢机制决定的,他的身体内有一个生物钟。人体处于各种运动状态(静止或运动、加速或减速)时,他的生物钟便会随着变化,或减慢,或加快,这便可以作为每个人自己带着的“时钟”。下面,我们首先用地球参考系来考察两个双胞胎在两次相遇之间的固有时。刘地一直停留在地球上没有移动,他的世界线是地球参考系中时间轴上的一段,这个参考系中,他的固有时也就等于坐标时,等于60年。而刘天的世界线是图2-12-2c右图中的OBD折线。折线中每一段的长度是20年,两段相加等于40年。所以,两个双生子在D点见面的时候,刘天40岁、刘地60岁。
从以上的分析可以体会到利用“固有时”来计算此类问题的方便之处。我们并不需要仔细考虑每个事件的过程,不需要详细去分析刘天的宇宙飞船哪一段是匀速,哪一段是加速,等等繁琐的细节,比如图2-12-2c右图中的另一条从O到D的弯弯曲曲的曲线,如果那是刘天的宇宙飞船的时空轨迹的话,只需要在地球参考系中计算这条线的固有时,那便就是刘天的年龄了。
如果不用地球参考系,使用宇宙飞船离开地球匀速运动的参考系,或者是返回时的匀速运动参考系,也都可以验证以上结果。三种情形得到同样结果:刘天40岁、刘地60岁。见图2-13-2。
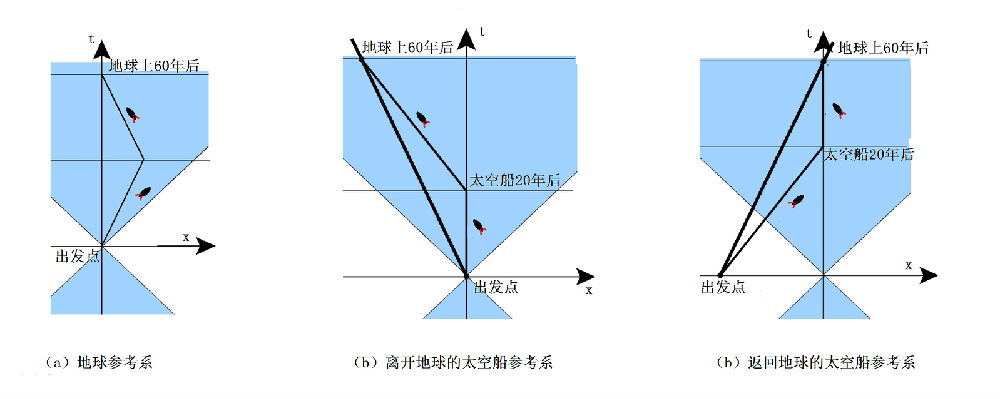
图2-12-3:使用不同的参考系计算双生子的年龄
http://blog.sciencenet.cn/blog-677221-838130.html 上一篇:相对论与黎曼几何-11-等效原理 下一篇:相对论与黎曼几何-13-四维时空 33 李颖业 沈律 应行仁 李泳 许文龙 王金良 薛加民 杜敏彪 董侠 王达伟 白冰 张凯军 罗德海 薛宇 鲍得海 王春艳 强涛 曹元兰 王迪 许旋风 罗会仟 李伟钢 文克玲 陈昌晔 ybyb3929 qiue yunmu luxiaobing12 eastHL2008 lengyonggang ychengwei koolp bishuiroubo该博文允许注册用户评论 请点击登录 评论 (19 个评论)
《数理同源2》-广义相对论与黎曼几何-1
|||
第二篇黎曼几何和广义相对论
1. 既古老又现代的几何学
几何是一门古老的学科。恐怕没有哪一门学科,像欧几里德几何学那样,在公元前就已经被创立成形,历经2000多年,至今还活跃在许多课堂上和数学竞赛试题中。尽管目前中国的中学教育已经不把平面几何当作必修课,一些学校删减了许多内容或者干脆取消了该门课程,但在上世纪的60-80年代,中国学生平面几何的水平肯定是算世界上比较高的。笔者还清楚地记得,解决平面几何难题,是本人中学时代的最爱。我们高中的数学老师兼班主任,是一个刚从师范毕业的年轻人,对数学教学充满热情。印象颇深的是他在黑板上画圆的绝活,他手握粉笔一挥一就,一笔下来,立刻在黑板上出现了一个规整的圆圈,用目测法很难看出这不是圆规画出来的。在他的影响下,我们班一半人都变成了数学迷,几何迷,大家在几何世界中遨游,从中体会到数学的奥妙,也感受到无限的乐趣。那两年,在教室的黑板上、课桌上,室外的石头边、树墩上,操场的篮球架上,随处可见同学们为思考几何题而画出来的三角形、直线、和圆圈。也许总体而言,中国式的教育方法忽略了发展学生改革创新的能力,但我深信,那个时代我们解决思考的无数道数学几何难题,对训练空间想象能力、逻辑推理能力,起了非常重要的作用。
纵观科学史,牛顿、爱因斯坦都是伟人,欧拉、高斯……伟大的数学家也可以列出不少,但恐怕很难找出像欧几里德这样的科学家,从2000多年前一直到现代,人们还经常提到以他命名的”欧几里德空间”、”欧几里德几何”等等名词,真可谓名垂千古而不朽了。阿基米德可能也能算一个,牛顿时代距离现在不过400来年,欧几里德和阿基米德却都是公元前古希腊时代的人物。
欧几里德的巨著—《几何原本》【1】(在1607年,有徐光启的中译本【2】),不仅仅被人誉为有史以来最成功的教科书,而且在几何学发展的历史中具有重要意义。其中所阐述的欧式几何是建立在五个公理之上的一套自洽而完整的逻辑理论,简单而容易理解。这点令人惊叹,它标志着在2000多年前,几何学就已经成为了一个有严密理论系统和科学方法的学科!
继欧几里德之后,16世纪法国哲学家、数学家笛卡儿(1596~1650年),将坐标的概念引入几何,建立了解析几何。
就平面几何而言,引入坐标的概念就是使用x、y来表示点、线、园等等图形在平面上的相对位置,因而便可以方便地应用解析的方法来处理几何的问题。如此一来,几何问题便成为代数的问题。这种处理方法使几何问题变得简单容易多了。说起来可笑,这种简单容易的方法反而使原来痴迷于求解平面几何难题的中学生们在刚学了解析几何之后,颇有一种失落感。因为解析几何使几何问题有了规范的解法,好像几何不再具有原来的魅力,原来那样有趣的几何学,被“解析”之后,突然间变得黯然失色、索然无味。
当然,谁也无法否认解析几何的诞生象征着几何发展的一个重要里程碑。解析几何不但能处理欧氏几何中的平面问题,还能解决三维空间的问题,以至于推广到更高维空间的几何问题。比如就说在二维和三维空间中吧,解析几何可研究的图形范围大大扩大。对平面曲线来说,欧氏几何中一般只能处理直线和圆。而现在有了坐标及函数的概念之后,直线可以用一次函数表示;圆可以用二次函数表示,二次函数不仅能够表示圆,还能表示椭圆、抛物线、双曲线等其它情形。除此之外,解析几何中还可以用一个任意的方程式f(x,y)=0,来表示所有的平面曲线,这些都使欧氏几何学望尘莫及。如果论及三维空间的话,在解析化之后,还能用三维坐标(x,y,z)和它们的代数方程式,表示各种各样的空间曲线和奇形怪状曲面。进一步谈到更高维的空间,欧几里德几何就更无用武之地了。
再到后来,数学的各个方面都有了巨大发展,特别是如我们在第一篇中所叙述的,牛顿和莱布尼茨发明了微积分,这是科学上的一件大事,使得那个时代的整个数学和物理都改变了面貌。那么,它对几何学的发展又有何种影响呢?
数学家们自然地将微积分这个强有力的工具用来研究几何学。实际上,微积分和几何的联系还更紧密一些,微积分的诞生也是得益于几何研究的,两者相互影响和发展。因此,微积分诞生之后不久,便有了“微分几何”这门新学科的萌芽。
法国数学家亚历克西斯·克莱洛(Alexis Clairaut ,1713 - 1763))是微分几何的先行者之一【3】。克莱洛是个名副其实的神童,他是母亲生下的20个子女中唯一一个长大成人的。在身为数学教授的父亲的严格管教和高标准要求下,克莱洛9岁开始读《几何原本》,13岁时就在法国科学院宣读他的数学论文。
之后几年,克莱洛迷上了空间曲线,他用曲线在两个垂直平面上的投影来研究空间曲线,第一次研究了空间曲线的曲率和挠率(当时被他称之为:双重曲率)。1729年,16岁的克莱洛将这个结果提交给法国科学院并以此申请法国科学院院士的资格,但当时未得到国王的立即认可。不过,只在两年之后,克莱洛发表了《关于双重曲率曲线的研究》一文,文中他公布了对空间曲线的研究成果,除了提出双重曲率之外,还认识到在一个垂直于曲线的切线的平面上可以有无数多条法线,同时给出了空间曲线的弧长公式,以及曲面的几个基本概念:长度、切线和双重曲率。这一年,18岁的克莱洛成为法国科学院有史以来最年轻的院士。
曲率和挠率是什么?我们先从平面曲线来认识曲率。

图2-1-1:克莱洛及双重曲率
我们首先需要引进曲线的切线,或称之为“切矢量”的概念,切矢量即为当曲线上两点无限接近时它们的连线的极限位置所决定的那个矢量。图2-1-1b中所标示的所有箭头,便是曲线的切矢量在曲线上各个点的直观图像。然后,再从图中切矢量沿着曲线的变化规律,又可以得到曲率的直观概念:曲率表征曲线的弯曲程度。比如说,图2-1-1b中最上面一条是直线,直线不会拐弯,其弯曲程度为0,即曲率等于0。这个0曲率与切矢量的变化是有关系的。看看直线上的箭头就容易明白了:上面所有箭头方向都是同样的。也就是说,曲率就是切矢量方向的变化率,或切矢量的旋转速率。直线上的切矢量方向不变,不旋转,对应于曲率为0。再看看图2-1-1b中下面两条曲线,当弧长增加时,切矢量不断旋转,曲线也随之而弯曲,切矢量旋转得越快,曲线的弯曲程度也越大。所以,曲率的几何意义就是曲线的切矢量对于弧长的旋转速度。
刚才在描述切矢量时,我们说它是“连线的极限位置所决定的那个矢量”,这儿我们很轻松地用上了“极限”的概念,诸位也毫不费力地就理解了它,因为大家学过了微积分。但是,在克莱洛的年代,曲率的计算可不是那么轻松容易的,这个十几岁的神童,天才地把微分的思想用于研究曲线,首次得到了这个结果。不仅如此,刚才我们讨论的只是平面曲线,克莱洛将微积分思想用于空间曲线。对一条平面曲线来说,如果每一点的曲率都确定了,这条曲线的形状便确定了。比如说,很容易直观地看出,一个圆上每个点的曲率都是一样的,等于它的半径的倒数。圆的半径越小,倒数则大,因而曲率便也越大;圆的半径越大,曲率则越小。因此,圆是等曲率的曲线,那么,现在我们考虑图2-1-2a中所示的平面螺旋线。因为平面螺旋线从内看到外,近似于一个一个从小到大的圆,所以,它的曲率是中心大边沿小。
我们可以将这个平面螺旋线想象成一个被压到一个平面上的的锥形弹簧,如果压力撤销之后,锥形弹簧恢复它的三维形状如图2-1-2b所示,这便得到了一条三维曲线。
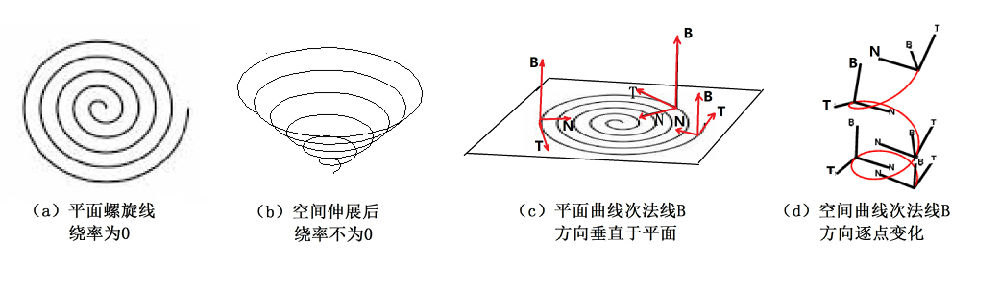
图2-1-2:空间曲线的挠率
首先让我们研究一下将平面螺旋线放在三维空间中的情形。如图2-1-2c所示,这时可以在曲线的每一个点定义一个由3个矢量组成的三维标架。令曲线的切线方向为T,在曲线所在的平面上有一个与T垂直的方向N。如果对于圆周来说,N的方向沿着半径指向圆心。N被称之为曲线在该点的主法线。为什么在法线的前面要加上一个“主”字呢,因为与切线T垂直的矢量不止一个,它们有无穷多个,都可以称为曲线在该点的法线,这些法线构成一个平面,叫做通过该点的法平面。刚才说过,这个事实是首先被小天才克莱洛认识到的。这所有的法线中,有一个是比较特别的,对平面曲线来说就是在此平面上的那一条法线,被称为主法线。有了切线T和主法线N,使用右手定则可以定义出三维空间中的另一个矢量B,B也是法线之一,称之为次法线。从图c很容易看出,螺旋线上每个点的切矢量T和主法线N的方向都逐点变化,唯有次法线B的方向不变。对一般的平面曲线也是如此,次法线的方向永远是垂直于曲线所在平面的,因此,一条平面曲线上每个点的次法线都指向同一个方向,即指向与该平面垂直的方向。
对一般的空间曲线,情况有所不同。想象一下让平面螺旋线中的每一圈逐渐从原来所在的平面慢慢被拉开,这时候,每一点次法线的方向便会从原来的垂直线逐渐发生偏离。也可以说,次法线的方向代表了与曲线“密切相贴”的那个平面,在一般三维曲线的情形下,这个密切相贴的平面逐点不一样,被称为曲线在这个点的“密切平面”。如图2-1-2d所示,对一般的三维曲线而言,在曲线上不同的点,三个标架T、N、B的方向都有所不同了。每一点的次法线B的方向也会变化,不过它仍然与该点的密切平面垂直。
克莱洛注意到空间曲线与平面曲线的不同,认为需要用另外一个曲率,后人称之为“挠率”的几何量来表征这种差别。换言之,挠率可以表示曲线偏离平面曲线的程度,被定义为次法线B随弧长变化的速率。
参考资料:
【1】Heath,Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile.Original publication: Cambridge University Press, 1925] ed.). New York: DoverPublications.
【2】1607Chinese translations reprinted as part of Siku Quanshu, or "CompleteLibrary of the Four Treasuries."
【3】O'Connorand, J. J.; E. F. Robertson (October 1998). "Alexis Clairaut".MacTutor History of Mathematics Archive. School of Mathematics and Statistics,University of St Andrews, Scotland. Retrieved 2009-03-12.
频谱分析是可能证明黎曼猜想的途径;复数放在“复球面”上,南极对应零点,北极对应无穷大点,其他的所有点对不为零的复数。 那么我应该说的是那个对应于北极的无穷大,它的四面八方都是接近复数无穷大的有限复数
频谱分析是可能证明黎曼猜想的途径
频谱分析是可能证明黎曼猜想的途径
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




No comments:
Post a Comment