|
.原載於數學傳播第二十三卷第三期 .作者當時任教於省立板橋高中 ‧對外搜尋關鍵字 |
|
在一個荒涼的島上,詩人少有能不空虛,而數學家則仍然能以其發現而自豪。 函數概念因為 Euler、d'Alembert(Jean le Rond d'Alembert, 1717~1783)以及 Daniel Bernoulli(1700~1782)一場歷經1760年代至1770年代、關於弦振動問題的論戰,而有了進一步的發展。 論戰的發起人是 d'Alembert。他的身世很可憐,剛出生時,就被遺棄在 Sanit Jean-le-Rond 教堂附近,恰巧被一位士兵發現,因此,就以教堂的名字為名。在d'Alembert 之前:雖然已經有人探討了弦振動(拉緊的弦)的問題,但是,只有 d'Alembert 在1747年所發表的論文「張緊的弦振動時形成的曲線的研究」(Recherches sur la courbe que forme unecorde tendue mise en vibration.Histoire de l'Acad'emie Royale, Berlin, 3. 1747. pp. 214-219),明確地將偏導數的概念引進,以作為弦振動的數學描述,因此,d'Alembert 也被稱做偏微分方程的先驅。 d'Alembert 主要探討的弦振動問題如下:設有一條長為 l 的弦懸掛並固定於
其中 a 為一比例常數,d'Alembert 證明了以(1)的解為
其中
然而,在 d'Alembert 心中所謂任一函數就現代意義而言,並非真的是任意的,而是有(3)式以外的附加條件!事實上,d'AIembert 要求初始函數 f(x) 至少要二次可微。因此,
|
把別的數學家置於Euler之上都是一種侮辱。 Euler於讀完 d'Alembert 的論文之後,也於1748年發表他關於弦振動問題的探討的論文──〈On the Vibration of Strings〉,文中的探討方法大致與 d'Alembert 相同,但是,Euler 的結論不同於 d'Alembert。Euler 認為 d'Alembert 對於函數的要求在物理上是不實際的,弦可以拉動:使得其起始形狀在不同的區間上可以由不同的解析表示式所描述。也就是說,Euler 認為他的初始函數 f(x) 在不同的區間上可以有著不同的解析表示式,而 Euler 稱此種函數為不連續函數(就現代意義而言是連續函數,但在相接的地方為不可微的)。Euler 這種函數的認知與他在《無窮小分析引論》中所提的函數的觀念完全不同,因此,他在1755年給函數下了一個新的定義:「如果某些量這樣依賴於另一些量,當後者變化時,它也隨著變化,那麼稱前者是後者的函數」。此一新的函數定義,似乎很接近現代的函數觀念,但是,Euler 的函數觀念,就現代意義而言,還是停留在導數有間斷點的函數上。無論如何,Euler 對於他的新發現,還是覺得很高興,他甚至於1763年12月20日寫信給 d'Alembert 說道:「考慮這類不服從連續性法則的函數:為我們開闢了一個全新的分析領域」。 |
用一條單獨的曲線,像表示棉花慣格而畫的曲線那樣,來描述在最複雜的音樂演出時效果……。在我看來是數學能力的極好證明。 介入這場論戰的另外一位重要人物是 Bernoulli 家族中最有才氣的 Daniel Bernoulli(1700~1782)。Daniel 是 Johann Bernoulli(1867~1748)的第二個兒子,Johann 雖然是在數學上很出名,而且是一個出色的數學教師,曾教育出像 Euler 這樣偉大的數學家。但是,他卻要 Daniel 去從商,或許是遺傳的關係,Daniel 並沒有如 Johann 所願,而是繼續從事學術研究,並在他的有生之年獲得了十次巴黎科學院的大獎(一個人若是得過一次,就算是非常優秀了),諷刺的是,他還在1734年,與他的父親以〈行星軌道與太陽赤道不同交角的原因〉論文一同獲得巴黎科學院的大獎,當然,他也以其豐碩的功績獲得其他榮譽以及外國院士的名聲。Daniel 於1721年獲得了醫學博士;1725年,與他的大哥 Nikolaus Bernoulli(1695~1726)受邀到俄國的聖彼得堡科學院工作,在那裡,Daniel 一共工作了八年(1725~1733),其間;大數學家 Euler 還曾擔任過他的助手。到了1733年,Daniel 的大哥過世以及一些原因,使得他離開聖彼得堡,但是,也是從那時候起,Daniel 與 Euler 開始了維持40年的通信。 早在1733午,Daniel 就曾明確指出振動的弦可以有較高頻率的振動:在1741~1743年所發表的關於振動桿的橫向振動論文中:又以物理的觀點說明基音和高次的諧音可以同時存在。直到讀完 d'Alembert 1774年與 Euler 1748年的論文之後,或許受到父親老約翰好勝的遺傳,Daniel 也趕緊於1753年發表他以前獲致的結果:振動弦的許多振動模式可以同時存在於弦上,也就是說,假定弦長為 l 的弦,則我們可以從第一基音、第二諧音、第三諧音……等一切可能的簡諧振動 出發,而將其疊合以獲致所有可能的振動
d'Alembert 知道 Daniel 的結論後,提出了強烈的反駁,他甚至不客氣地說:他根本不相信一切奇的週期函數能表示成「Daniel 級數」。Euler 知道 Daniel 的結論後,雖然提出了反駁,但是,基於他與 Bernoulli 家族的情感(Euler 起碼是老約翰的學生,Daniel 又曾推荐他在聖彼得堡科學院的工作),因此,他是以含蓄地方式提出反駁:首先他讚揚 Daniel 發現許多簡單的振動模式可以同時存在,也就是同一條弦可以同時發出許多諧音的物理觀點,但是,Euler 並不認為每一條起始曲線 f(x)=y(x,0),都可以用一個無窮三角級數表示,也就是說,他無法接受
Euler 不肯認同的原因是很簡單的,他認為他自己的振動弦的解包括了所有可能的函數,特別是他所謂的不連續函數,因此,連續的正弦函數怎麼可能疊加產生不連續函數(這在現代意義下:當然是有問題的!),另外一方面,正弦函數是奇函數,因此,顯然無法產生所有的任意函數,特別是如果起始曲線 f(x) 有一部份是靜止的;但是,Euler 倒是願意承認 Daniel 的解是他的解的一部份。 Daniel 對 Euler 提出的反駁的回答是:既然有無窮多個 an 可供選擇,因此:每一個函數當然均可用一三角級數表出,甚至於正如同他在1773年表示的看法:三角級數可能在不同的區間表示不同的代數函數。於是,他的解所涵蓋的範圍比Euler 廣。Daniel 這種非數學方式的論證,當然是無法使人信服,大家或許可以看出,爭議的焦點其實是在於何種函數可以展成三角級數的問題上。無論如何,Daniel 是第一位堅持任意函數可以表示成一三角級數和的人,這種觀點至少為往後的 Fourier 級數奠定物理的基礎。 |
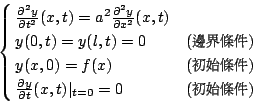
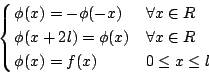
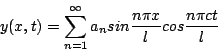
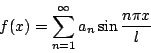
No comments:
Post a Comment