Thursday, February 6, 2014

tw01 group01 群論與魔方：高階魔方的性質與公式 群論的起源

  1. [PDF]

  2. 集合論與現代數學 - 交通大學應用數學系

  1. jupiter.math.nctu.edu.tw/~smchang/9802/BM_SM.pdf‎


  1. tor的集合論在數學中引進兩種新事物, 一個. 是集合, 一個是無窮。 前者給20世紀數學帶. 來一大批新學科, 它們可以統稱為結構數學,. 如抽象代數(包括群論、 環論、 域 ...

    1. 群論的起源

    1. episte.math.ntu.edu.tw/articles/sm/sm_17_07_2/‎

    一般而言，若G是一個集合(不管有限或無限)，而對應於其中任兩元素g1，g2，都有一元素g1g2，稱為g1，g2兩元素的合成，並且滿足以上四個條件，則稱G為一個群。

    1. 第三次數學危機-模型論-16

    1. 159.226.2.2:82/gate/big5/www.kepu.net.cn/gb/.../4_44_1016.htm‎

    這個理論可以說是泛代數(當然也包含通常代數中的群論、環論、域論等等)，它們 ... 起就由數論、分析、集合論的問題所推動，強調研究一階邏輯所有公式的集合模型。

群論與魔方：高階魔方的性質與公式

chowkafat.net/Rubik11.html‎


請注意從集合論的角度看，「軌道」實質上是集合X上的「等價類」(equivalence class)。換句話說，一個「軌道」中的成員就是那些在G的「作用」下可互相映射到對方的成員 ...


群論的起源
曹亮吉 		 

  「群」這個觀念在數學及自然科學中都非常重要，而它的起源則是為了解方程式。 一次、二次方程式的解法很早就為人所熟悉。高次方程式的解法有兩個方向。其一為數字係數方程式的數值近似解，這種方法最早在中國發展得很完善。另一種則為文字係數方程式的根式解，它在十六世紀上半因義大利一些數學家解決了三次及四次的問題，而掀起了高潮。 一般的三次方程式都可以經由移根的處理，而變成x3+px+q=0。若以ω表1約三次方根 $\frac{(-1+\sqrt{-3})}{2}$，則此方程式的三根為

\begin{displaymath}x_1=u+v,x_2=u\omega +v\omega ^2,x_3=u\omega ^2+v\omega \end{displaymath}


其中

\begin{displaymath}u=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} \quad v=\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\end{displaymath}


這些公式都是由係數經四則運算及開方運算表示出來的，所以說三次方程式有根式解四次方程式一樣有根式解，雖然其公式比三次的要複雜得多。 當三次及四次方程式獲解後，大家的注意力自然就轉到五次方程式。 在這方面，雖然經過十七、十八兩世紀的努力，但幾乎都交了白卷。 直到十八世紀末的Lagrange (1736-1813年)，才算有些突破。他經由方程式根的置換觀點，把四次以下的方程式給予統一的解法。 先以三次方程式為例。令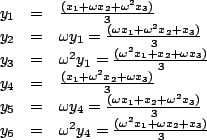
\begin{array}{rcl} y_1 & = & \frac{(x_1+\omega x_2+\omega ^2x_3)}{3}\\ y_2 & = ... ...3}\\ y_6 & = & \omega ^2y_4=\frac{(\omega ^2x_1+\omega x_2+x_3)}{3} \end{array}
考慮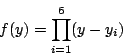

\begin{displaymath} f(y)=\prod ^6_{i=1} (y-y_i) \end{displaymath}


則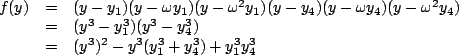
\begin{array}{rcl} f(y) & = & (y-y_1)(y-\omega y_1)(y-\omega ^2y_1)(y-y_4)(y-\om... ...(y^3-y_1^3)(y^3-y^3_4)\\ & = & (y^3)^2-y^3(y_1^3+y_4^3)+y_1^3y_4^3 \end{array}
將(x1,x2,x3)的順序重排，就稱為xi的一個置換， 譬如(x1,x2,x3)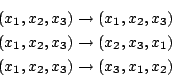$\rightarrow$(x3,x1,x2)就是一個置換。 而在xi的置換之下，y1變成了y2，y2變成了y3， 而y3變成了y1，因此我們得到y1，y2， y3的一個置換(y1,y2,y3)$\rightarrow$(y2,y3,y1)。 同理，xi的置換(x1,x2,x3)$\rightarrow$(x3,x1,x2)也引起y4, y5,y6的一個置換 (y4,y5,y6)$\rightarrow$(y5,y6,y4)。xi的置換一共有6個， 它們把y1分別變到yi。 這6個置換中有三個

\begin{eqnarray*} &(x_1,x_2,x_3)\rightarrow(x_1,x_2,x_3)\\ &(x_1,x_2,x_3)\rightarrow(x_2,x_3,x_1)\\ &(x_1,x_2,x_3)\rightarrow(x_3,x_1,x_2) \end{eqnarray*}


引起y1，y2，y3間的置換，使y13=y1y2y3不變;也引起y4,y5,y6間的置換， 因比也使 y43=y4y5y6不變。但另外三個xi的置換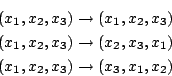

\begin{eqnarray*} &(x_1,x_2,x_3)\rightarrow(x_1,x_3,x_2)\\ &(x_1,x_2,x_3)\rightarrow(x_2,x_1,x_3)\\ &(x_1,x_2,x_3)\rightarrow(x_3,x_2,x_1) \end{eqnarray*}


則使y1,y2,y3與y4,y5,y6兩者之間互變。這就說明了xi無論怎麼置換， f(y)的係數y13+y43及y13y43總是不變，所以它們是xi的對稱式，因此可以寫成為原方程式係數的有理式。 經計算可得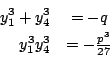

\begin{eqnarray*} y_1^3+y_4^3&=-q\\ y_1^3y_4^3&=-\frac{p^3}{27} \end{eqnarray*}


f(y)是y3的二次式，稱為原方程式的預解式，因為由f(y)=0，我們可以解得y13及y43，再從y1、y4(它們正是前面所提到的u及v)及 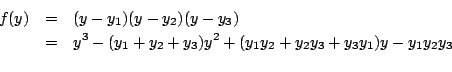$0=\frac{(x_1+x_2+x_3)}{3}$，就可以得到三根的公式。 這種利用根置換求得根式解的方法可以用到四次方程式。解四次方程式時， 若令 $y_1=\frac{(x_1+ix_2-x_3-ix_4)}{4}$，$i=\sqrt{-1}$為1的四次方根，則xi的24個置換，會把y1變成yi， $1\leq i \leq 24$。這24個yi分成六組，每組10個，組員之間所差的是i的倍數，譬如y1，y2=iy1，y3=iy2，y4=iy3為一組。組員的乘積，譬如 y1y2y3y4=y14，為預解式的一根。可惜這樣的預解式為六次，所以行不通。 然而y1的選擇並不是那麼死板。我們可以試xi的任何有理式。若令 y1=x2x3+x1x4，則xi的24個置換只能使y1變成y1， y2=x1x3+x2x4或 y3=x1x2+x3x4，而任何一個xi的置換一定引起yi的置換。所以

\begin{eqnarray*} f(y) & = & (y-y_1)(y-y_2)(y-y_3)\\ & = & y^3-(y_1+y_2+y_3)y^2+(y_1y_2+y_2y_3+y_3y_1)y-y_1y_2y_3\\ \end{eqnarray*}


的係數在xi的置換之下是不變的，因此是原來四次方程式 x4+ax3+bx2+cx+d=0的係數的有理式。由計算可得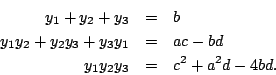

\begin{eqnarray*} y_1+y_2+y_3&=&b\\ y_1y_2+y_2y_3+y_3y_1&=&ac-bd\\ y_1y_2y_3&=&c^2+a^2d-4bd. \end{eqnarray*}


如此，我們就可以解出預解式f(y)=0的三個根y1,y2，y3。因 y1=x2x3+x1x4及 x1x2x3x4=d為已知，所以x2x3，x1x4可解。又由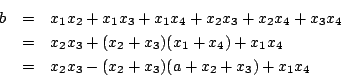

\begin{eqnarray*} b &=& x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4 \\ &=& x_2x_... ...x_3)(x_1+x_4)+x_1x_4 \\ &=& x_2x_3-(x_2+x_3)(a+x_2+x_3)+x_1x_4 \end{eqnarray*}


我們得到x2+x3的二次式，所以x2+x3可解。最後從x2+x3及x2x3可解得x2。其他根的求法類似。 Lagrange成功地用根的置換觀點，解了三次及四次方程式後，自然用同樣的方法試著去解五次方程式。為了進一步了解這種嘗試，我們用濃縮的表示法來代替所談的置換。譬如 $(x_1,x_2,x_3)\rightarrow (x_3,x_1,x_2)$表示根是依 $x_1 \rightarrow x_3 \rightarrow x_2 \rightarrow x_1$，這種方式置換的，就以(1,3,2)表之。如果置換為 $(x_1,x_2,x_3)\rightarrow (x_2,x_1,x_3)$，則以(l，2)(3)表之，而簡寫為(1,2)。如果置換為 $(x_1,x_2,x_3)\rightarrow (x_1,x_2,x_3)$，則以(1)代替(1)(2)(3)來表示。請注意:括號內的數字是環狀排列的，因此 (10xA14130xA1412)=(3,2,1)=(2,1,3)。 三個根的置換一共有6個:(1),(1,2),(2,3),(1,3),(1,2,3),(1,3,2)。它們之間可以做合成的運算。譬如先做置換(1,2)，再做置換(1,3,2)，則x1先變成x2，再變成x1，x2先變成x1，再變成x3，而x3先是不動，再變成x2所以合成的結果為 (1)(2,3)=(2,3)。設G表由此6個置換所形成的集合，則合成的運算有如下的性質：
一、若g1，g2在G內，則其合或g1g2也在G內。
二、若g1，g2，g3在G內，則 ((g1g2)g3)=(g1(g2g3))。(結合律)
三、G中有一元素e[=(1)]，它有如下的性質:eg=ge=g，對所有G中的元素g都對。
四、若g在G內，則G中必有一元素g-1，使得 gg-1=g-1g=e。(g-1稱為g的逆元素。)
一般而言，若G是一個集合(不管有限或無限)，而對應於其中任兩元素g1，g2，都有一元素g1g2，稱為g1，g2兩元素的合成，並且滿足以上四個條件，則稱G為一個群。 群的例子很多，上述所言三個根的置換就成為一個群，稱為三階置換群。又如，整數(或有理數)在加法合成之下成為一個群;非0有理數在乘法合成之下也成為一個群等等。群的合成運算雖然符合結合律，但卻不一定符合交換律。譬如，在三階置換群中， 我們已經看過 (1,2)(1,3,2)=(2,3)，然而倒過來合成，則 (1,3,2)(1,2)=(10xA1413)。 現在我們以群的觀點重看三次方程式的解法。 我們以S3表示此三階置換群。讓H表S3中的元素使y13， y43不變者(即，讓y1，y2，y3互變;y4，y5，y6互變者)， 則

H=(1),(1,2,3),(1,3,2)


在H中仍然有合成運算，而且仍然滿足群的四個條件，所以H也是一個群。但H含於S3中，而且所用的合成運算相同，所以我們說H是S3中的一個子群。在S3中而不在H的元素集合可表成為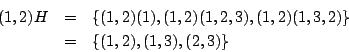

\begin{eqnarray*} (1,2)H &=& \{ (1,2)(1),(1,2)(1,2,3),(1,2)(1,3,2)\} \\ &=& \{ (1,2),(1,3),(2,3)\} \end{eqnarray*}


它使y13變成y43，而使y43變成y13。簡單地說，H，(1,2)H都可以看成預解式兩根y13,y43的置換。 再看四次方程式。我們以S4表示相應的四階置換群。它的元素一共有24個，我們以下表列出:

\begin{displaymath} \begin{tabular}{\vert c\vert c\vert c\vert c\vert c\vert c\v... ...ries{m}\selectfont \char 98}}&6&8&3&6&1\\ \hline \end{tabular}\end{displaymath}


所謂類型(1,2,3,4)是指四個數字都出現在同一括弧內者,如(1,2,3,4)等,一共有 $\frac{4!}{4}=6$個(環狀排列).其餘類型的意義類推. 在S4中讓 y1=x2x3+x1x4, y2=x1x3+x2x4, y3=x1x2+x3x4都不變者,仍然組成一個子群.

H={ (1),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)}


在S4中而不在H的元素可分成五個子集合(不是子群):

(1,2)H,(1,3)H,(2,3)H,(1,2,3)H,(1,3,2)H


連H[=(1)H]共有6個子集合，而同一子集合中的元素都引起y1,y2,y3 間同樣的置換。因此這6個S4的子集合都可看成預解式三根y1,y2,y3 的置換; $(1)H\rightarrow(1)\in S_3$, $(1,2)H\rightarrow (1,2)\in S_3$,$\cdots\cdots$, $(1,3,2)H\rightarrow (1,3,2)\in S_3$。 上述S3及S4的H都有如下的性質:gH=Hg對任何g都成立。具有這樣性質的子群稱為正規子群。 如果把三次及四次的想法，拿來看五次方程式， 則我們要找根xi的有理式yi,$1\leq i$$\leq m$$\leq4$。 然後令H為五階置換群S5中使yi都不變的子群， 然後把S5分成為幾個子集合Hi,i=1,…,k的聯集。 同一個子集合的元素所相應於yi的置換都相同，而不同的子集合相應於不同的置換， 因此子集合的個數k不能超過m!個;事寶上k要為m!的約數。 同時每個子集合的元素個數和H的一樣多， 所以H的元素個數正好是S5的元素個數120的約數。此外， H要為S5的正規子群。從進一步的群理論，我們知道， 除S5及{ (1)}兩個子群外，S5只有一個正規子群A5， 其元素個數為60。所以符合上述條件的H只可能是S5或A5， 而其相應的yi的個數m就要為1或2。但可證明對一般的五次方程而言， 這是不可能的;也就是說，我們找不到適當的yi， 所以用Lagrange的方法無法找到五次方程式的根式解。雖然這並不就證明五次方程式不能有根式解， 但卻給這樣的結論提供了強烈的暗示。 受了Lagrange的影響，日後Abel(1802-1829年)終於證明了一般的五次以上方程式沒有根式解，而Galois(1810-1831年)對一個給定的特殊方程式，「何時有根式解，何時則否」，也能根據根的置換原理，而有一定的判斷準則。 由於Lagrange、Abel及Galois等人的努力，根式解方程式的問題終於告了一個段落。然而為了解決這個問題所引起的群理論的探討，本身卻成為現代代數學的一支。經過一個半世紀的演變，群論本身不但有豐富的內涵，而其觀念與應用不只是遍及數學各個角落，而且更侵入了晶體學、化學、物理等領域。
 
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)