方程根式可解若且唯若它的Galois 群可解, 當然我們在這
裡不解釋什麼叫群, 什麼是Galois 群。Abel 與Galois 不僅解決了三百年來無法解決的著名
難題, 更重要的是: 為了解決這個問題, 他們建立起了「體」(field) 與「群」(group) 的概念
group as expressed in different coordinate systems
http://w3.math.sinica.edu.tw/math_media/d301/30103.pdf
http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/page2.html
C 為包含在
"微積分第二講" 龔昇
微积分五讲龚升_百度文库
wenku.baidu.com/view/c5f7cfd1240c844769eaee90.html?from=related
Green 定理與應用 (第 6 頁) 林琦焜
這定理告訴我們要計算積分值
雅克比(Jacobian)矩阵_彭乾坤_新浪博客
blog.sina.com.cn/s/blog_5ea558b60100fj4v.html
轉為繁體網頁
一個函數之微分的積分值等於該函數之邊界值的差。換句話說方程式(1)把區間的積分與作用於其「零維」(zero dimension) 邊界之上的「積分」(零維的積分是該點之值)連繫起來,這零維的邊界是兩個端點 a 與 b
Green 定理與應用 (第 6 頁) 林琦焜
|
.原載於數學傳播第二十一卷第四期 .作者當時任教於成功大學數學研究所 ‧對外搜尋關鍵字 |
![\begin{displaymath}
\begin{array}[b]{lll}
\overrightarrow{v}(t) = & \frac{d\over...
...2x}{dt^2} , \frac{d^2y}{dt^2} \right )
\end{array} \eqno{(33)}
\end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/img101.gif) 設物體的質量為 m,其所受外力的合力為 F,則由牛頓定律知 則對 F 而言從 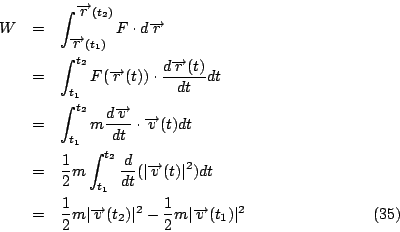 其中 合力對物體所作的功等於動能的改變量。如果 F 為一保守力場, 則(32)式改寫為 其中 |
其中 J(t) 就是 Jacobian 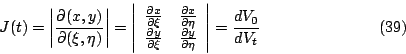
因此 同理可得 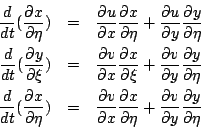 J(t) 對 t 微分並利用行列式之性質可得  所以 J(t) 滿足一階微分方程; Euler 展開公式: 這公式稱為 Euler 展開公式 (Euler expansion formula),由微分方程知 由此式顯然可得 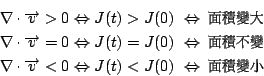 因此我們稱一流體為不可壓縮 (incompressible) 其真實意義: 流體經過任何的變換其形狀雖然改變了,但其面積(或體積)卻始終保持不變。 |
為向量場 F=(u,v) 環繞封閉曲線 C 之環流,利用等式 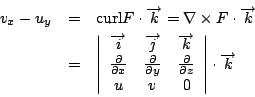 我們可將前一式表為 假設 表示單位面積之環流,因此 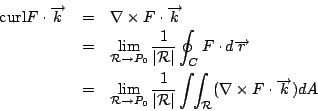 所以向量場 F 之旋度
|
實數系的建構 Cauchy-Schwarz 不等式之本質與意義 Green定理與應用 棣美弗定理與Euler公式 凸函數、Jemsen不等式與Legendre變換 數、十進位與Cantor集 從三角求和公式到Fourier級數 Weierstrass逼近定理 談加減消去法 從等比級數談起 凸函數、Jensen不等式與Legendre變換
雅可比矩阵
雅可比矩阵
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此,雅可比矩阵类似于多元函数的导数。
假设F:Rn→Rm
是一个从欧式n维空间转换到欧式m维空间的函数。这个函数由m个实函数组成: y1(x1,...,xn), ..., ym(x1,...,xn).
这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵,这就是所谓的雅可比矩阵:
此矩阵表示为:
这个矩阵的第i行是由梯度函数的转置yi(i=1,...,m)表示的
如果p是Rn中的一点,F在p点可微分,那么在这一点的导数由JF(p)给出(这是求该点导数最简便的方法)。在此情况下,由F(p)描述的线性算子即接近点p的F的最优线性逼近,x逼近与p
编辑] 例子
由球坐标系到直角坐标系的转化由F函数给出:R × [0,π] × [0,2π] → R3
此坐标变换的雅可比矩阵是
R4的f函数:
其雅可比矩阵为:
此例子说明雅可比矩阵不一定为方矩阵。
编辑] 在动态系统中
编辑] 雅可比行列式
如果m =
n,那么F是从n维空间到n维空间的函数,且它的雅可比矩阵是一个方块矩阵。于是我们可以取它的行列式,称为雅可比行列式。
在某个给定点的雅可比行列式提供了F在接近该点时的表现的重要信息。例如,如果连续可微函数F在p点的雅可比行列式不是零,那么它在该点具有反函数。这称为反函数定理。更进一步,如果p点的雅可比行列式是正数,则F在p点的取向不变;如果是负数,则F的取向相反。而从雅可比行列式的绝对值,就可以知道函数F在p点的缩放因子;这就是为什么它出现在换元积分法中。
例子
设有函数F
则它的雅可比行列式为:
从中我们可以看到,当x1和x2同号时,F的取向相反;该函数处处具有反函数,除了在x1
= 0和x2 = 0时以外。
|
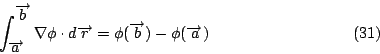
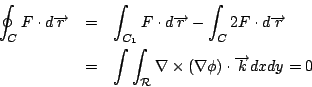
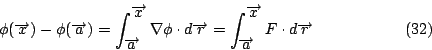

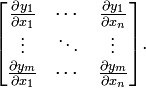
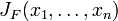 ,或者
,或者 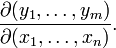
 }-
}-
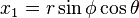





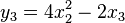



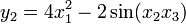
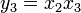
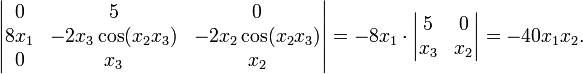
No comments:
Post a Comment