|||
k是群体数的线性增长率,与出生率有关。想到这点,我们恍然大悟:如果k比较大,群体繁殖得太多了,数目增长太快,增加社会不稳定的因素,当然就容易造成混乱
k是群体数的线性增长率,与出生率有关。想到这点,我们恍然大悟:如果k比较大,群体繁殖得太多了,数目增长太快,增加社会不稳定的因素,当然就容易造成混乱
第十九章﹕从有序到混沌
让我们仔细考察上一章中的图(18.2),复习一下罗伯特·梅的结论。从图中我们看到:可以将系统的长期行为大概归类于几种情况。或者说,可将图中的曲线分成特征不同的几个部分:
1. 当k小于1的时候,xn的最后极限是0,表明出生率太低,出生的数目补偿不了死亡数, 种族最终走向灭绝。例如,k=0.8,因为x0=0.1,不难算出x1=0.072,x2=0.051,……,对应的群体数分别是1000、720、510……,绝对群体数将逐年减少,最后趋于0。这种情况,连种族都灭亡了,显然也不存在什么混沌魔鬼。
2. 我们更感兴趣k大于1的情形,这时,方程中的第一项使得群体数逐年增长,而第二项使得群体数不能增长到无限大。我们将k值从1到3的那段绿线称为‘平衡’期,因为在这种情形下,生死速率旗鼓相当, 最后的群体数将平衡于一个固定值。比如,k=1.2,这时的线性增长率为120%。那么,许多年之后,这种生物会有多少呢?从x0开始,可以算出:x1=0.108,x2=0.1157,……。因而,相应的绝对群体数是1000,1080,1157,……。可以证明,若干年之后,这种生物的群体数将趋向于一个固定值:1666。所以,k值从1到3的情况下,种族数收敛到固定值,完全是经典情况,没有看见混沌魔鬼。
3. 当k=3.8,从迭代可以得到相应的绝对群体数是1000,3420,……,6547,9120,3100,8120,……。这时的最后结果很奇怪,不会收敛到任何稳定状态,而是在无穷多个不同的数值中无规则地跳来跳去。也就是说:魔鬼跳出来了,系统走向混沌。
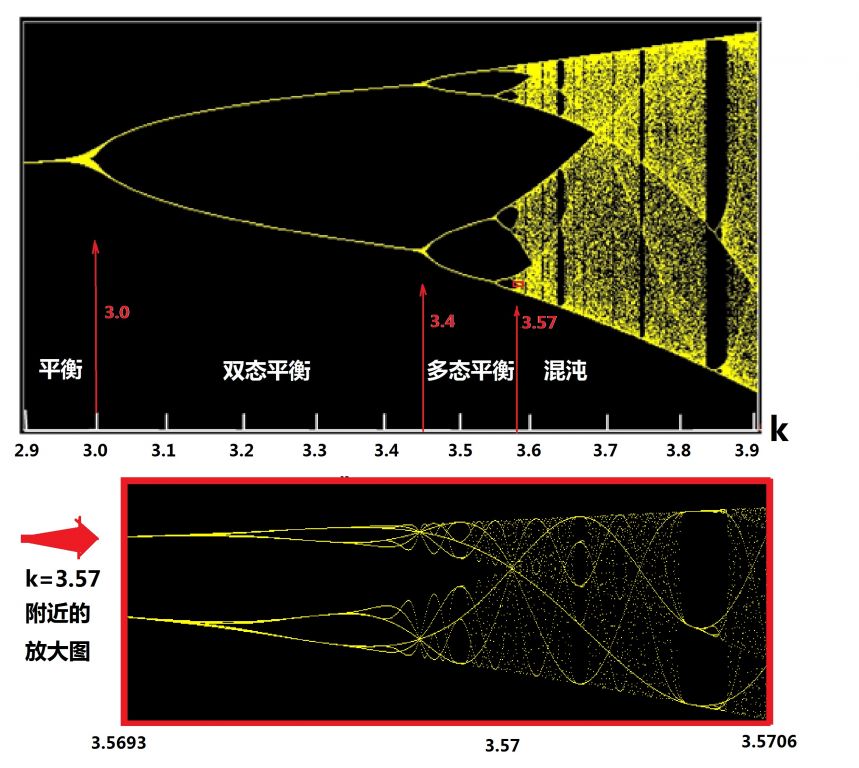
上面的第一、二种情况,属于经典有序,第三种,则为混沌。因而,我们最感兴趣的是中间从k=3到k=3.8的一段,我们再将这段放大来研究,即可得到图(19.1)中上图所示的曲线。
逻辑斯蒂系统是如何从有序过渡到混沌的呢?从图(19.1)的上图中可看到,即使我们让k的数值平滑地增长,系统的长期行为却不‘平滑’。当k的数值在3附近的时候,系统来了个‘突变’:原来的一条曲线分成了两支,形成一个三岔路口! 然后,k的数值继续平滑增长,到3.45附近时,又走到了三岔路口,两条曲线分成了四支,再后来,分成了八支,十六支……分支越来越多,相邻三岔路口间的距离却越来越短,最后,以至于我们的眼睛无法清楚地分辨那些三岔路口及分支为止。
现在,可能很多读者已经有了直觉:混沌魔鬼是由这些越来越多的分岔现象产生出来的!完全没错,这也是当时罗伯特·梅的结论。人们将这种分岔现象叫做‘倍周期分岔’现象(Bifurcation)。‘周期’这个词是哪儿冒出来的呢?想想我们所研究的逻辑斯蒂方程(18.3),这是个一代一代(或者说一年一年)的迭代方程,那么,一年就是一个周期。我们观察k=3到k=3.4之间的曲线,也就是在图(19.1)中标示为‘双态平衡’的那一段),所谓‘双态平衡’ 意味着,迭代到最后,每年的群体数将在两个数值之间循环。也可以说, 系统回到原来状态的周期从一年变成了两年,周期加倍了!后来,从k=3.4到k=3.57,状态数越来越多,最终的群体数将在更多的数值之间循环, 因此,系统回到某一平衡状态的周期因加倍又加倍而变得越来越长,这是图中标示为‘多态平衡’的一段。
当k增加到3.57之后, 由于分支之间的交互缠绕, 已无法区分单独的分支, 倍周期分岔现象呈崩溃之势, 平衡点已无法区分,连接成一片连续区域。这意味着最终的群体数失去了周期性, 进入图中标示为‘混沌’的范围。点击图(19.1),可链接到JAVA演示程序,用鼠标右键画个小矩形,便可将k=3.75附近区域放大,得到图(19.1)中下面的图形。
上面所描述的系统状态随着参数的变化从平衡走向混沌的过程, 不仅仅出现在生态学中,而是一个普遍现象。倍周期分岔现象是系统出现混沌的先兆,最终会导致有序到无序, 稳态向混沌的转变。我们在前面章节中介绍洛伦茨吸引子时,洛伦茨方程中也有一个参数,那是叫做瑞利数的R。瑞利数表征了大气流的粘滞性等物理特征。当时,洛伦茨在他的系统中所用的瑞利数R=28,得到了混沌现象。对某些其它的R值,有混沌解,也有非混沌解。因此,当R平滑变化时,在洛伦茨系统中,也能观察到倍周期分岔现象,从而观察到系统从有序过渡到混沌的过程。
科学家们更为深入地研究倍周期分岔图, 总结出倍周期分岔现象具有自相似性及普适性等等重要而有趣的特征。
自相似性是显而易见的。如果将图(19.1)中的倍周期分岔曲线在不同的标度下进行放大, 仔细观察, 就会发现它实际上是一种分形, 一种具有无穷嵌套的自相似结构, 或所谓标度不变性: 即用放大镜将细节部分放大若干倍后,它仍与整体具有相似的结构。这个与内在随机性密切相关的几何性质揭示了倍周期分岔现象与分形、混沌、奇异吸引子等之间的内在联系。
我们将在下一章继续讨论倍周期分岔现象的其他有趣特性。
《走近混沌》-20-混沌魔鬼‘不稳定’ 精选
精选


《走近混沌》-20-混沌魔鬼‘不稳定’
|||
王二正在总结他的演讲,谈到他计划中的毕业论文课题:
“你们知道,我们这个由各类生物群体组成的大千世界,盘根错节、繁杂纷纭;天下万物,互相制约、互相依存;自然界中形形色色的动植物不停地出生、繁殖、变化、死亡,时而大浪淘沙、优胜劣汰;时而又相辅相成、维持平衡。在永不间断的争争斗斗、生生死死中, 各种生物群体的数目变化莫测,有时侯表现一定程度的周期性, 有时侯又貌似一片混沌,的确有些类似于上两章中所研究的逻辑斯蒂方程的解的行为。我正在想,用逻辑斯蒂方程为基础,是否可能找出一个描述包括多种生物竞争,群体数如何变化的生态模型来……”
王二的想法引起了好几个生物相关专业学生的兴趣,他们聚在一起开始热烈讨论生态学的问题。
其实,逻辑斯蒂方程不仅在生态研究方面意义重大,在别的领域也有诸多应用。是啊,逻辑斯蒂映射看起来太简单了,只有1个变量,1个方程,却能表现出混沌系统的种种特征。还记得我们曾经讨论过的其它混沌系统,比如洛伦茨系统和三体问题吗?相对于它们的原始问题来说,最后的方程也算够简单了,但是,仍然有三个变量、三个微分方程。
混沌理论的老祖宗庞加莱曾经提出一个定理,稍后被瑞典数学家本迪克松证明,说的是混沌现象只能出现在三维以上的连续系统中。但这个定理不适用于离散系统,逻辑斯蒂迭代方程所描述的就是一个特别简单的1维离散系统。混沌魔鬼在这个简单系统中轻巧地跳出来,成为混沌研究者们的最爱。
李四对此深有体会,因为他正在做一个与流体力学、湍流等有关的课题,涉及的系统很复杂。当系统维数太多想不清楚时,李四就总是回到最简单的一维逻辑斯蒂方程,用图形的方法来考虑问题,感觉容易多了。不过,张三今天却说:
“总的来说,1个变量的确比3个变量简单很多。不过,有时候,3维的图像也挺直观的。比如说你看,当我用计算机画奇异吸引子的时候,画出来的洛伦茨吸引子多漂亮!洛伦茨方程的解,是随时间变化而无限绕下去、却又永不重复的轨道,在三维空间中画出来,好像一只翩翩起舞、展翅欲飞的蝴蝶。可是,这个逻辑斯蒂方程的吸引子,用图形表示就不好看了。”
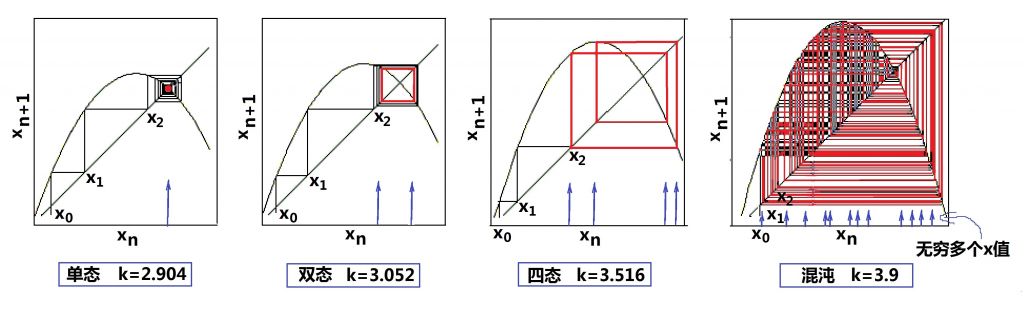
张三的说法不无道理。对逻辑斯蒂方程来说,每个不同的k值都有一个吸引子,在‘平衡’区域,吸引子是1个固定点;在‘双态平衡’区域,吸引子是2个固定点;在‘多态平衡’区域,吸引子是多个分离的固定点;而在‘混沌’区域,吸引子是连成一片的点;最后的状态在这些点无规律地蹦来蹦去,到底是如何蹦的?分岔图上对具体过程显示得并不清楚。不过,我们可以用如图(20.1)所示的逻辑斯蒂迭代图,清楚地看到在不同k值下,迭代过程中xn的收敛情形。
图(20.1)中,标为红色的是迭代的最后过程。图中的抛物线对应于逻辑斯蒂方程右边的非线性迭代函数(xn+1 = kxn·(1-xn))。
从左向右看:第一个小图中的xn最后收敛于一个红点;第二个小图中的xn最后收敛于一个红色矩形,标志着有两个不同的x值;而第三个小图中的xn最后收敛的红色区域,是在4个不同的x值中循环;最右边的‘混沌’情况,大家一看圈来圈去的红色曲线便明白了:有点类似于洛伦茨的蝴蝶图了,这是魔鬼现身的表现!

图(20.1):不同k值下的逻辑斯蒂迭代图
逻辑斯蒂系统还有一个少有的优点:它所对应的微分方程可以求得精确的解析解。而大多数非线性系统是无法得出精确解的,只能用迭代法来研究数值解的定性性质,以及解的稳定性。
混沌魔鬼的出现,与参数k的数值有关,k越大,魔鬼出现的几率就越大。这其中有何奥秘呢?我们回到逻辑斯蒂方程描述的生态学,回忆一下参数k的意义是什么?k是群体数的线性增长率,与出生率有关。想到这点,我们恍然大悟:如果k比较大,群体繁殖得太多了,数目增长太快,增加社会不稳定的因素,当然就容易造成混乱,令魔鬼现身啰。

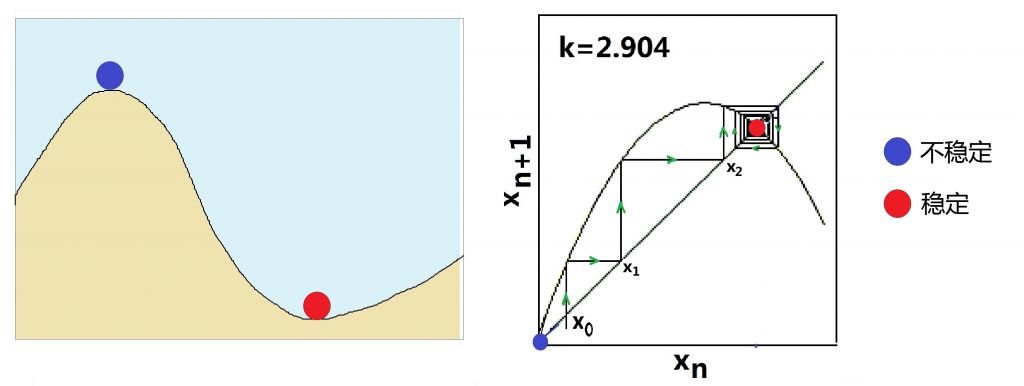
图(20.2):不稳定和稳定
混沌的产生的确与方程的‘稳定性’有关,因此,我们有必要讨论讨论系统状态的稳定性。哪种状态是稳定的?哪种状态是不稳定的?从图(20.2)的左图中一目了然,那是在重力场中‘稳定’和‘不稳定’的概念:对小圆球来说,坡顶和坡谷都是重力场中可能的平衡状态。但是人人都知道,位于顶点的蓝色球不稳定,位于谷底的红色球很稳定。究其根源,是因为只要蓝色球开始时被放斜了那么一丁点儿,就会因不能平衡而掉下去。而红球呢,则不在乎这点起始小误差,它总能够滚到谷底而平衡。用稍微科学一点的语言来说,稳定就是对初值变化不敏感,不稳定就是对初值变化太敏感。我们将这个意思发挥扩展到逻辑斯蒂方程上,考虑图(20.2)的右图中k=2.9时,即吸引子是一个固定点的情况。这时,逻辑斯蒂方程的解应该是图中的抛物线和45度直线的交点,图中的这两条线有两个交点。因此,除了固定吸引子x无穷=0.66之外,x无穷=0也是一个解。但是,在图中所示的条件下,x无穷=0.66是稳定的解,x无穷=0却是不稳定的解。为什么呢?因为只要初始值从0偏离一点点,像图中所画的情况,迭代的最后结果就会一步一步地远离0点,沿着绿色箭头,最终收敛到x无穷=0.66这个稳定的平衡点。
研究三体问题的大数学家庞加莱,是微分方程定性理论的始创者。有关微分方程解的稳定性问题,则由另一位数学家李亚普洛夫始开先河。亚历山大·李亚普洛夫(1857-1918)是与庞加莱同时代的俄国数学家和物理学家。与稳定性密切相关的李亚普洛夫指数,便是以他命名。
如何来判定系统稳定与否?李亚普洛夫想,可以用对重力场中两个小球是否稳定的类似判定方法。于是,他研究当初值变化一点点时,看看系统的最终结果如何变化,并以此来作为稳定性的判据。更具体地说,我们可以将系统的最终结果x无穷表示成初始值x0的函数,用图形画出来。然后,系统的稳定性取决于这个函数图形的走向:它是更接近图(20.3)中的哪一种曲线呢?是向下指数衰减(λ小于0)?还是向上指数增长(λ大于0)?还是平直一条(λ等于0)?第一种情况被认为是稳定的,第二种情况被认为是不稳定的,而λ等于0则是临界状态。这儿的λ便是李亚普洛夫指数。

图(20.3):指数函数的性质随λ变化
图(20.4)显示的便是不同k值下,逻辑斯蒂系统的李雅普诺夫指数及对应的分岔图,从中不难看出λ的符号变化与倍周期分岔的产生及混沌魔鬼出现之间的关系:k值比较小的时候,λ小于0,系统处于稳定状态;从k=3.0开始,λ有时等于0,出现分岔现象,系统变到多态平衡,但仍然是稳定的,大多数时候,λ小于0;从k>3.57开始,λ开始大于0,系统不稳定,过渡到混沌。有趣的是,混沌魔鬼露脸后又经常躲藏起来。在λ大于0的区间中,λ的数值还经常返回到小于0的数值。也就是说,混沌有时又变成有序,这对应于分岔图中(黄色图像)中的空白地带。

图(20.4):逻辑斯蒂系统的李雅普诺夫指数及对应的分岔情形
No comments:
Post a Comment