下载
ishare.edu.sina.com.cn/download.php?fileid=18169719
Monte Carlo Simulation of Neutron Shielding for ... - DSpace@MIT
dspace.mit.edu/.../1721.../42254993.pdf?...
Massachusetts Institute of...
Loading...
by MR Folkert - 1998 - Related articles
Monte Carlo Simulation of Neutron Shielding for Proton. Therapy Facilities by. Michael R. Folkert. SUBMITTED TO THE DEPARTMENT OF NUCLEAR ...Demon algorithm
From Wikipedia, the free encyclopedia
The demon algorithm is a Monte Carlo method for efficiently sampling members of a microcanonical ensemble with a given energy. An additional degree of freedom, called 'the demon', is added to the system and is able to store and provide energy. If a drawn microscopic state has lower energy than the original state, the excess energy is transferred to the demon. For a sampled state that has higher energy than desired, the demon provides the missing energy if it is available. The demon can not have negative energy and it does not interact with the particles beyond exchanging energy. Note that the additional degree of freedom of the demon does not alter a system with many particles significantly on a macroscopic level.
The microcanonical ensemble is a collection of microscopic states which have fixed energy, volume and number of particles. In an enclosed system with a certain number of particles, energy is the only macroscopic variable affected by the microphysics. The Monte Carlo simulation of a microcanonical ensemble thus requires sampling different microscopic states with the same energy. When the number of possible microscopic states of thermodynamical systems is very large, it is inefficient to randomly draw a state from all possible states and accept it for the simulation if it has the right energy, since many drawn states would be rejected.
1. Perform a random change in the state of a randomly chosen particle (e. g. change velocity or position).
2. Calculate the change in energy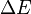
of the thermal system.
3. Negative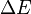, i. e. excess energy, is given to the demon by adding 
to the demon. This case (
) is always accepted.
4. The demon provides positive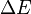 to keep the total energy constant only if it has sufficient energy, i. e. 
. In this case the change is accepted, otherwise the randomly chosen change in velocity is rejected and the algorithm is restarted from the original microscopic state.
5. If the change is accepted, repeat the algorithm for the new configuration.
Since energy fluctuations per degree of freedom are only of order 1/N, the presence of the demon has little effect on macroscopic properties of systems with high numbers of particles. After many iterations of the algorithm, the interplay of demon and random energy changes equilibrates the system. Assuming that a particular system approaches all possible states over very long times (quasi-ergodicity), the resulting Monte Carlo dynamics realistically sample microscopic states that correspond to the given energy value. This is only true if macroscopic quantities are stable over many Monte Carlo steps, i. e. if the system is at equilibrium.
Contents
[hide]Motivation[edit]
In thermodynamical systems, equal macroscopic properties (e. g. temperature) can result from different microscopic properties (e. g. velocities of individual particles). Computer simulations of the full equations of motion for every individual particle to simulate microscopic properties is computationally very expensive. Monte Carlo methods can overcome this problem by sampling microscopic states according to stochastic rules instead of modeling the complete microphysics.The microcanonical ensemble is a collection of microscopic states which have fixed energy, volume and number of particles. In an enclosed system with a certain number of particles, energy is the only macroscopic variable affected by the microphysics. The Monte Carlo simulation of a microcanonical ensemble thus requires sampling different microscopic states with the same energy. When the number of possible microscopic states of thermodynamical systems is very large, it is inefficient to randomly draw a state from all possible states and accept it for the simulation if it has the right energy, since many drawn states would be rejected.
The demon algorithm[edit]
The full procedure can be summarized by the following steps:1. Perform a random change in the state of a randomly chosen particle (e. g. change velocity or position).
2. Calculate the change in energy
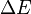of the thermal system.3. Negative
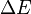, i. e. excess energy, is given to the demon by adding to the demon. This case () is always accepted.4. The demon provides positive
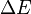to keep the total energy constant only if it has sufficient energy, i. e. . In this case the change is accepted, otherwise the randomly chosen change in velocity is rejected and the algorithm is restarted from the original microscopic state.5. If the change is accepted, repeat the algorithm for the new configuration.
Since energy fluctuations per degree of freedom are only of order 1/N, the presence of the demon has little effect on macroscopic properties of systems with high numbers of particles. After many iterations of the algorithm, the interplay of demon and random energy changes equilibrates the system. Assuming that a particular system approaches all possible states over very long times (quasi-ergodicity), the resulting Monte Carlo dynamics realistically sample microscopic states that correspond to the given energy value. This is only true if macroscopic quantities are stable over many Monte Carlo steps, i. e. if the system is at equilibrium.
See also[edit]
- Monte Carlo methods
- Metropolis algorithm to sample microscopic states at a fixed temperature
 | This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations. (January 2011) |
References[edit]
- Harvey Gould and Jan Tobochnik and Wolfgang Christian (2006). "Chapter 15: Monte Carlo Simulations of Thermal Systems". An Introduction to Computer Simulation Methods: Applications to Physical Systems (3rd Edition). Addison Wesley. ISBN 978-0-8053-7758-3.
- Creutz, Michael (May 1983). "Microcanonical Monte Carlo Simulation". Phys. Rev. Lett. (American Physical Society) 50 (19): 1411–1414. Bibcode:1983PhRvL..50.1411C. doi:10.1103/PhysRevLett.50.1411.
No comments:
Post a Comment