Wednesday, February 12, 2014

qm01 white01 对两个费米子系统，出现‘正反’的概率是1。

对两个费米子系统，出现‘正反’的概率是1。

tianrong1945的个人博客分享http://blog.sciencenet.cn/u/tianrong1945

博文

“傻”博士的初恋-23-全同粒子（科普）精选

已有 3308 次阅读 2013-1-28 09:43 |个人分类:故事+谜语|系统分类:科普集锦|关键词:玻色全同粒子费米子玻色-爱因斯坦凝聚

第二十三章﹕全同粒子（科普）

2001 年 11 月 3 日，星期六

“萨沙，我们该写数学科普书的最后一章了。你想好了写些什么内容吗？” 我问。这时候，已经是下午四点钟，萨沙刚起床，洗完了澡，坐在计算机旁边发呆。

我见他不回答我的问题，又问了一遍。

“我……这不，也在想这件事吗。”

萨沙又说：“你看，这儿有一则新闻。CLAY数学研究所，去年曾经發佈一則消息：將提供百萬美元的獎金為七個現未解決的數學問題征求答案。”

“真的吗？每个問題都一百萬美元吗？”

“对。”

“CLAY数学研究所在哪儿呀？”

“那是美國麻省劍橋的一個非盈利教育基金會。你在MIT没听过吗？”

“没有。”

“每个問題都是很难解决的。比如这一个，是在計算機算法領域頗為著名的 P / NP 問題。”

“这我知道。我們在第一章內提到過的‘推銷員周游世界’的問題，不就和这有关系吗？”

“我记得在去年年底的《科学美国》上，为了配合CLAY数学研究所的百万大奖，美国著名的科普作家Ian Stewart 写了一篇文章，把P/NP 问题与微软视窗系统中的一个小游戏联系起来。没准儿玩游戏也能得百万大奖哦！”

“哪一个游戏呀？”

“叫做MINESWEEPER…”

“啊，探雷游戏。我经常玩的那一个。”

誰不想成為百萬富翁呢？既然CLAY数学研究所以此问题征求百万大奖，当然说明这是一个非常重要和困难的问题。不过，玩游戏倒不困难，还挺有趣的。于是，我便开始收集资料：从探雷游戏出发，再解释计算机的算法问题，再就是量子计算机，那是我不太懂的领域，可能得请教学物理的罗德了。

自从上次和罗德在一起吃中饭时谈到萨沙之后，我和他的谈话反倒自然了。因为现在我不需要回避他什么，而完全是作为一个知心朋友互相倾诉。人是需要听众的，特别是当你在感情问题上有困扰时。这些天，我们经常在一起畅所欲言，开诚布公。我对他谈到和萨沙的恋爱经过，萨沙的种种趣事。我们也谈到互相的家庭、小时候的事、同学、朋友等等。

2001 年 11 月 20 日，

于是，今天向罗德咨询量子计算机之事，我首先谈到计算机算法中的 NP 問題。

“什么是NP 問题？”罗德虽然是软件工程师，但是学物理出身，并未修过很多计算机课，我便大概介绍了一下。

“哦，这量子计算机，和你的算法問題又有什么关系呢？” 罗德感到奇怪。

“算法問題的实质是计算速度的问题。从理论上来说，现在的这种经典类型的计算机永远处理不了Non-P問題，也就是那些计算量按指数增长的問題。而未来的，按照量子规律来运行的量子计算机就可以处理Non-P問題。”

“为什么呢？”

“因为……因为，量子现象不是和经典现象完全不同吗？其实，我也不是很懂，……。但是我想，我们可以慢慢讨论。对这个问题，你这个学物理的，肯定会理解得比我更深刻。”

我记起了第一个提出量子计算机设想的人，就是诺贝尔物理学奖得主，生前任教于美国加州理工学院的物理学家理查德•费曼。

“啊，费曼，那是一个智慧超凡的科学鬼才……”罗德很熟悉费曼的故事：“他不仅是著名物理学家，也是一位开保险箱专家和邦戈鼓手。此外，他还曾经像一位真正的画家一样卖掉过自己的好几幅绘画作品。他研究生刚毕业，就参加了第一颗原子弹的曼哈顿计划。我还看过好几本与他的经历有关的通俗读物，很有意思。”

不过，罗德对费曼提出的量子计算了解不多。我告诉他，1981年五月，在MIT召开了连接物理学和计算机技术的第一次会议，费曼在会上作了一个“Simulating Physics With Computers”的报告，从此揭开了研究发展量子计算机的新篇章。

说到MIT，罗德的兴趣来了，说是MIT有个物理教授沃尔夫冈·克特勒，几年前实现了玻色-爱因斯坦凝聚的那个，得了今年的诺贝尔物理学奖哦！不久前，好象是10月9日吧，瑞典皇家科学院宣布的，MIT的克特勒与其他两位科学家，共同分享2001年的诺贝尔物理学奖。

罗德说：“我不懂量子计算机，不过，我先给你讲讲与这三个人做的工作有关的玻色子及费米子，让你对量子的行为有点初步概念吧。”

下面便是罗德讲的有关‘全同粒子’概念。哈哈，还加上我这个物理门外汉，提出的几个愚蠢问题。

世界上有一模一样的东西吗？有，那就叫“全同粒子”！

所谓全同粒子就是质量、电荷、自旋等内在性质完全相同的粒子。在宏观世界中，可能不存在完全一模一样的东西，即使看起来一模一样，它们也是可以被区分的。因为根据经典力学，即使两个粒子全同，它们运动的轨道也不会相同。因此，我们可以追踪它们不同的轨道而区分它们。但是，在符合量子力学规律的微观世界里，粒子遵循测不准原理，没有固定的轨道，因而无法将它们区分开来。量子力学中，有两种类型的全同粒子：玻色子和费米子。分别以玻色和费米两位物理学家而命名。它们分别服从玻色-爱因斯坦统计和费米-狄拉克统计规律。

我插嘴了：“爱因斯坦是人人皆知的大师，费米和狄拉克也都在诺贝尔奖的榜上有名，可这个玻色是谁，没听过啊……”

“玻色的确不是那么有名，印度人，属于第三世界的物理学家嘛，受很多条件所限，不过，由他而命名的玻色子在物理学界还是挺有名的。对玻色子统计规律的研究可能是玻色一生中唯一一项重要的成果……”

有趣的是，玻色是因为一个“錯誤”而发现玻色子的。1921年左右，在一次有关光电效应的讲课中，玻色犯了一个类似“掷两枚硬币，得到“正正”概率为三分之一”的那种错误。没想到这个错误却得出了与实验相符合的结论，也就是不可区分的全同粒子所遵循的一种统计规律……

我不明白，什么叫“掷两枚硬币，‘正正’概率为三分之一”的那种错误呀？另外，两个粒子可区分或不可区分，会影响概率的计算吗？”

“当然会影响啊。”罗德说。

你先看在现实生活中计算概率的情况。如果我们掷两枚硬币，因为每个硬币都有正反两面，所有可能的实验结果就有四种情况：正正、正反、反正、反反。如果我们假设每种情形发生的几率都一样，那么，得到每种情况的可能性，各是四分之一。

现在，想象我们的两枚硬币变成了量子硬币。也就是说，它们完全一模一样，而且不可区分。既然不可区分，‘正反’和‘反正’就是一样的，所以，所有可能发生的情形就只有“正正”“反反”“正反”三种情形。

这时，如果我们仍然假设三种可能性中每种情形发生的几率是一样的（尽管这好像不太符合我们的日常经验，但不要忘记，我们考虑的是‘量子硬币’！），我们便会得出“每种情况的可能性，都是三分之一”的结论。这个例子就说明了，多个“一模一样、无法区分”的物体，与多个‘可以区分’的物体，所遵循的统计规律是不一样的。

玻色以此计算方法，得到了与光电效应实验相符的结果。他立刻意识到，这是一个“没错的错误”！便继续深入钻研下去，1924年写出一篇《普朗克定律与光量子假说》的论文。然而，当初没有杂志愿意发表这篇论文，认为玻色犯了统计学家们看来十分低级的错误。

后来，玻色突发奇想，直接将文章寄给大名鼎鼎的爱因斯坦，不料立刻得到了爱因斯坦的支持。玻色的“错误”之所以能得出正确结果，因为光子就正是一种不可区分的、后来被统称为‘玻色子’的东西。对此，爱因斯坦心中早有一些模糊的想法，如今玻色的计算正好与这些想法不谋而合。于是，爱氏便将这个概念，延伸应用到其它类似的粒子。这些‘类似粒子’之后被人称为‘玻色子’，这也才有了现在名为“玻色-爱因斯坦统计”，以及2001年三个诺贝尔物理奖得主所证明的，超低温下实现的“玻色-爱因斯坦凝聚”理论。

遗憾的是，玻色本人呢，却像一颗划过天空闪亮一时，又转瞬即逝的彗星一样，之后在科学上便没有什么大作为，最终也与诺贝尔奖无缘。

我似懂非懂：“啊，原来光子就是玻色子。不可区分的全同粒子算起概率来的确与经典统计方法不一样。那么，费米子又是些什么玩意儿呢？”

不同微观粒子的全同性有所不同，是来源于它们的自旋，及此自旋导致的不同对称性。玻色子是自旋为整数的粒子，比如光子的自旋为1。两个玻色子的波函数是交换对称的。也就是说，当两个玻色子的角色互相交换后，总的波函数不变。另一类称为费米子的粒子，自旋为半整数。例如，电子的自旋是二分之一。由两个费米子构成的系统的波函数，是交换反对称的。也就是说，当两个费米子的角色互相交换后，系统总的波函数只改变符号。（见下图中的右边二图）

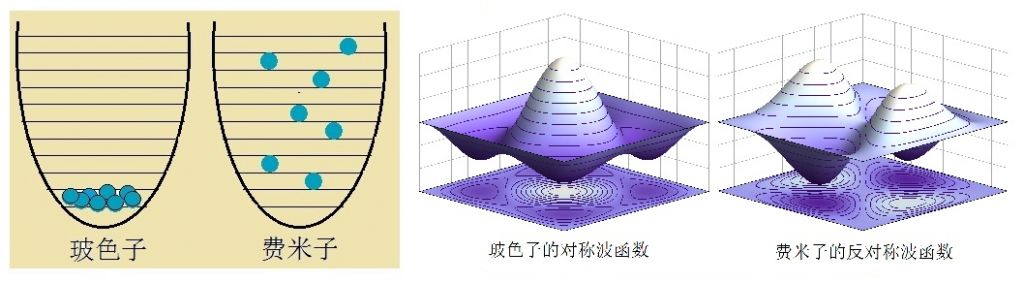
我又不明白了：“费米子交换后波函数变号，不是好像可以区分两个费米子了吗？怎么它们也是全同粒子呢？”

不是那样的，罗德说，交换前和交换后的波函数，虽然相差了一个符号，但它们描述的仍然是同样的状态，因为两种情形下的几率波（波函数的平方）是一样的。所以，费米子也是一种不可区分的全同粒子。

罗德又说，多个费米子系统的波函数是反对称函数这点，使得它的统计规律与玻色子的又有所不同哦！

“怎么不同法呢？”

我先打个比方吧。两个玻色子的互换波函数对称，就表明两个玻色子可以处于同样的状态下而和平共处；两个费米子的互换波函数反对称，就表明两个处于同样状态的费米子将互相残杀。或者说，玻色子是一群友好的朋友；费米子是互相排斥的一个个独立大侠。如果有一伙玻色子去住汽车旅馆，它们愿意大家共处一室，住一间大房间就够了；而如果一伙费米子去住汽车旅馆，便需要供给它们每人一间独立的小房间。

我突然有点开窍，想起了过去学元素周期表时听过的‘泡利不相容原理’，便问罗德：“那个泡利原理是不是与费米子的特性有关啊？”

对呀，罗德说，正是如此。所有费米子都遵循这一原理，包括电子。因而，原子中的任意两个电子不能处在相同的量子态上，而是在原子中分层排列（见上图左图）。在这个基础上，才得到了有划时代意义的元素周期律。

然后，再以刚才的两个硬币为例，说明费米子的统计规律有何特别之处？两个硬币现在变成了‘费米子硬币’。对两个费米子来说，因为它们决不愿意共住一间房间，也就是不可能处于完全相同的状态，所以，四种可能情形中的‘正正’和‘反反’状态都不成立啦，只留下唯一的一个可能性：‘一正一反’。因此，对两个费米子系统，出现‘正反’的概率是1。

我还想急于知道与今年诺贝尔物理奖有关的“玻色-爱因斯坦凝聚”是怎么回事，可罗德说那有点太专业了。不过，可以如此稍加理解……

因为玻色子喜欢大家同居一室，大家都拼命挤到能量最低的状态。比如，光就是一种玻色子，因此，许多光子可以处于相同的能级，所以，我们才得到了激光这种超强度的光束。“玻色–爱因斯坦凝聚”就是原子在冷却到绝对零度附近时所呈现出的一种特别物态……

我脑袋中又闪出一个笨问题：“光子是玻色子，电子是费米子，原子是玻色子还是费米子啊？”

啊，刚才没说太清楚。原子是复合粒子，情况要复杂一点。对复合粒子来说，如果由奇数个费米子构成，则为费米子；由偶数个费米子构成，则为波色子。如为波色子的原子，在一定的条件下，降低温度到接近绝对零度，所有玻色子像是突然‘凝聚’在一起，那时会产生一些平常物质中观察不到的‘超流体’有趣性质，这就是“玻色-爱因斯坦凝聚”。通过对“玻色-爱因斯坦凝聚”的深入研究，有可能实现‘原子激光’之类的前景诱人的新突破。

罗德最后总结说：“全同粒子的玻色子或费米子行为，也可以说是量子力学中最神秘的侧面之一！”　

今天，给萨沙看了看我根据罗德的叙述写的‘奇妙的量子’一节。对量子现象的难以理解，萨沙似乎不以为然，还发表了几句哲学家式的论调。

他说：“怪非怪，常为怪；不怪有怪，怪有不怪。这世界上的每件事都是奇怪的，不怪的东西才奇怪呢。”

“什么话嘛！奇怪的人。”

“对，人也是一样，每个人都很古怪。”

我不想和他辩论。心想，真是个怪人！和古怪的量子现象一样古怪，一样难以理解，琢磨不透，我想起了不确定原理、不可区分的全同粒子……，我又觉得，不知道为什么，和这个人交往了这么久，好象仍然不是很了解他。特别是在他的中国公司搞出了点眉目之后，萨沙有些想法与过去不一样，而且很不合常理。满口、满脑袋只有‘公司’。

“和你的公司谈恋爱去吧！”有一次，我赌气地说。

“是呀，这恐怕马上就要成为事实啰！明年，我可能大部分时间都得呆在北京。”没想到他会这样回答。