Maciej Trzetrzelewski
y
Abstract
Black-Scholes equation, after a certain coordinate transformation,
is equivalent to the heat equation. On the other hand the relativistic
extension of the latter, the telegraphers equation, can be derived from
the Euclidean version of the Dirac equation. Therefore the relativistic
extension of the Black-Scholes model follows from relativistic quantum
mechanics quite naturally.
We investigate this particular model for the case of European
vanilla options. Due to the notion of locality incorporated in this way
one nds that the volatility frown-like e
ect appears when comparing
to the original Black-Scholes model
6 Summary and Outlook
Relativistic extensions of the Black-Scholes model seem very natural,
considering future development of high frequency trading. However
the physical bound on the maximal speed of the asset is, to our understanding,
still too high to give noticeable e
ects in the market. On
the other hand, as we argued in the introduction, the e
ective maximal
speed of log-returns, c
, is much smaller due to the "resistance"
of the market - an analogous phenomena appears in some physical situations.
Therefore relativistic extensions with such e
ective velocity,
instead of the real one, seem reasonable.
m
In this paper we considered a certain relativistic extension of the
Black-Scholes model, based on the observation that the Black-Scholes
equation, in particular coordinates, becomes a heat equation. The latter
is clearly non relativistic and therefore it is a good starting point
for relativistic extensions. The stochastic process behind the heat
equation is a Brownian motion, which implies that an appropriate extension
should be related to a process such that in the c
! 1 limit
the Wiener process is recovered. A very well known process which
satis es this condition is the telegrapher process. Not only does it
converge to the Wiener process in the above limit but also, it incorporates
the features of relativity in a very clever way: the system
of PDEs describing the probability densities of the telegrapher process
is equivalent to the Euclidean version of the Dirac equation in
1 + 1 dimensions. Therefore it provides an extremely elegant framework.
Our most important nance-related conclusion based on these
remarks is that the geometric Brownian motion should be replaced by
its relativistic counterpart (13)
dS
t
=S
t
= dt + c
m
(1)
N(t)
dt;
where N(t) is the number of events in the homogeneous Poisson process
with rate parameter . This SDE becomes the geometric Brownian
motion with volatility when the c
! 1 limit is performed
(keeping = c
2
m
=
2
m
). It is not an Ito process and therefore one cannot
use the Ito lemma to derive the corresponding equation for a derivative
instrument. We circumvent this problem by claiming that in order
to price a vanilla option one should replace the Gaussian probability
distribution by its relativistic counterpart. If this is the case then
the pricing formula is given by Eq. (17). By performing numerical
integration we have found that equation (17) in general violates put-
23
m
call parity. However there is a region of parameters (in particular for
large c
) for which arbitrage possibilities are small. In these cases the
volatility frown e
ect is observed as expected. We then evaluated the
1=c
2
m
m
corrections to the Black-Scholes formula, using Eq. (17), and
found that the corresponding implied volatility resembles the frown
shape which is in accordance with the previous numerical analysis.
There are several direction where one can improve our results and
the model itself. One is to perform thorough Monte Carlo simulations
based on the SDE (13) which could then be compared with numerical
results of Section 5 as well as with (25). Formula (17) was nowhere
proven to be the solution of option pricing based on (13). It may
very well be that the true solution is di
erent form (17), and that
it does not violate put-call parity as (17) does. Still, it is desirable
to bring the integral (17), for arbitrary c
, to a form similar to the
Black-Scholes pricing formula. This seems possible as the integrand
involves the Bessel function and its time derivative, which have many
special properties.
m
Second, it would be very interesting to derive a counterpart of the
Ito lemma for the process (13) as it could be used to derive the pricing
PDE from rst principles.
Lastly one could generalize the process (13) by using non-constant
e
ective velocity c
(because it is e
ective there is a priori no reason
to assume that it is constant). Clearly one could also consider a
stochastic process for c
m
dc
2
m
m
(e.g. some mean-reverting process)
=
(c
m
; t)dt + (c
which, together with (13) and the constraint c
m
; t)dW
2
m
t
=
2
, would result
in a certain generalization of the stochastic volatility models. The
randomness of volatility would then be explained by the randomness
of c
m
since d
2
=
1
dc
2
m
. Furthermore one can also consider a nonhomogeneous
Poisson process (i.e. with non constant ) therefore
adding one more degree of freedom to the model
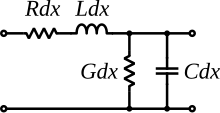
Telegrapher's equations
From Wikipedia, the free encyclopedia
The telegrapher's equations (or just telegraph equations) are a pair of linear differential equations which describe the voltage and current on an electrical transmission line with distance and time. The equations come from Oliver Heaviside who in the 1880s developed the transmission line model, which is described in this article. The model demonstrates that the electromagnetic waves can be reflected on the wire, and that wave patterns can appear along the line. The theory applies to transmission lines of all frequencies including high-frequency transmission lines (such as telegraph wires and radio frequency conductors), audio frequency (such as telephone lines), low frequency (such as power lines) and direct current.
Schematic representation of the elementary components of a transmission line.
The telegrapher's equations, like all other equations describing electrical phenomena, result from Maxwell's equations. In a more practical approach, one assumes that the conductors are composed of an infinite series of two-port elementary components, each representing an infinitesimally short segment of the transmission line:
Contents
[hide]Distributed components[edit]
No comments:
Post a Comment