「超分辨荧光显微技术」指的是哪些呢?与普通的荧光显微技术相比,实现了哪些技术突破?以及具体应用于哪些工作场景?为该工作的开展带来了怎么样的改变?
brain01 由于光的衍射,物体上的点如 P、Q,在相机上并不是单独的点,而是一个个有一定大小的斑,被称为夫琅禾费衍射斑(或称艾里斑),如右侧的同心圆所示
brain01 由于光的衍射,物体上的点如 P、Q,在相机上并不是单独的点,而是一个个有一定大小的斑,被称为夫琅禾费衍射斑(或称艾里斑),如右侧的同心圆所示
7 个回答
私货已经在另一个答案(如何评价2014年诺贝尔化学奖?)里面吐槽过了,来认真写个答案吧。第一次写同时面向非专业和专业人士的科普长文,希望没看明白的同学留言指出,我尽量修改,谢谢!
------------------------------------------------
2014 年的诺贝尔理综奖颁发给了“超分辨荧光显微技术”。也许接下来的几天,媒体会关注 Stefan Hell、Eric Betzig 二人的传奇经历,或者另一名华人女科学家与该奖项失之交臂的遗憾。但是八卦之外,这项成果背后的科学本身也非常有意思。
这里面有三个关键词:“超分辨”、“荧光”和“显微技术”,我希望能够解释清楚以下几个问题,尤其是后两个问题:
1. 为什么需要(光学)显微技术?
2. 为什么光学显微镜的分辨率存在理论极限?
3. 用怎样的方法可以突破这个理论极限以达到“超分辨”?为什么这个理论极限可以被突破?
4. 为什么非得是荧光显微技术,而非普通的明场(透射光)显微技术?
1. 采样定理与显微镜
我们用肉眼观察或者用相机拍摄一个物体时,物体上的每一个细微的点都会在眼睛的视网膜或是相机的感光芯片上成像。那么我们为什么不能看到细菌等微小的东西,为什么不能把照片无限放大以看清远处树木上面的每一片叶子呢?
这个问题的答案比较简单:因为组成视网膜的每一个感光细胞(视杆细胞和视锥细胞)、相机芯片上的每一个感光元件(CCD、CMOS等)都是有大小的。比如视网膜中央凹区域的视锥细胞直径平均约为 5 微米。而由于奈奎斯特-香农采样定理的限制,视网膜上能分清的两个相邻像点的距离是视锥细胞直径的两倍,即 10 微米。再结合眼球的构造,大致可以推断出,在距离眼睛 25 厘米的位置,我们能分辨物体上相距为 80 微米的两个点,换算成点阵密度就是大约 320 ppi,这也是苹果所谓“视网膜屏”分辨率的来历。
如果要观察小于 80 微米的物体,比如细菌,就需要先将物体放大,再用眼睛或者相机观察。现代光学显微镜的构造其实非常简单,样品放置在物镜的焦点处,从样品上发射或散射的光经过物镜变成平行(准直)光,再经过一个结像透镜,然后会聚到相机的感光芯片上成像。
按照前面的方法来推算,要区分物体上相距为 200 纳米的两个点,如果使用科研级相机,比如最近火起来的 sCMOS 相机(每个感光像素尺寸为 6.5 微米),只需要使用放大倍率为 65 倍的物镜就足够了。
那么是否可以通过提高物镜的放大倍率来观察低于 200 纳米的物体,比如细胞里面微管呢?
答案是不可以。
2. 光学衍射极限
由于光是一种电磁波,具有衍射和干涉的特性。
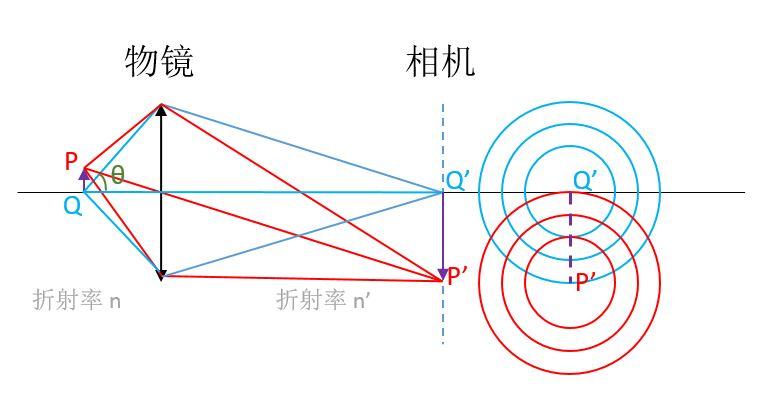 图 1. 光学显微镜简化示意图
图 1. 光学显微镜简化示意图
如上面的简图所示,紫色箭头表示的物体 PQ 经过物镜等之后在相机上成像为P'Q'。由于光的衍射,物体上的点如 P、Q,在相机上并不是单独的点,而是一个个有一定大小的斑,被称为夫琅禾费衍射斑(或称艾里斑),如右侧的同心圆所示。那么,当 P'、Q' 相距太近的时候,两个斑会叠加导致难以分辨。这就要求物体上的 P、Q 要相距一定的距离。
1873 年,德国物理学家、卡尔蔡司公司的恩斯特·阿贝(Ernst Abbe)首次推算出衍射导致的分辨率极限。根据瑞利判据——“当一个像斑的中心落到另一个像斑的边缘时,就算这两个像刚好能被分辨”,显微镜能分辨的物体上两点 P、Q 的最小距离 h 为:

这个公式就是光学显微镜的分辨率公式,或称为光学衍射极限。(注意此处的分辨率与通常说的显示器分辨率含义不同)
其中, 为光的波长,n 为物方的折射率,
为光的波长,n 为物方的折射率, 为物体与物镜边缘连线和光轴的夹角。如上图所示。为方便起见,其中的
为物体与物镜边缘连线和光轴的夹角。如上图所示。为方便起见,其中的  通常称为数值孔径,简写为 NA。
通常称为数值孔径,简写为 NA。
摄影领域常用 f/# 或称光圈值来描述镜头,光圈值与数值孔径可以相互换算。对于一枚光圈为 2.0 的镜头来说,数值孔径为 0.25,其分辨能力约 1.2 微米。
目前常用的高倍物镜 NA 最大为1.49,可以算出,对于可见光,比如波长 500 纳米的绿光,显微镜的分辨率约为 200 纳米。所以,即使再提高物镜的放大倍率,也不能提高显微镜的分辨率。
而 200 纳米这个数值也就通常被称作衍射极限。
2.5. 光学衍射极限的动态范围
从上面的公式可以看到,光学衍射极限其实并不是一个具体的数值,如果改变上述公式中的参数,是可以有效提高分辨率的。
(1) 光的波长
可见光波长范围是400~760 nm,如果使用更短波长的光,比如紫外线,理论上可以提高分辨率。但是紫外线能量高,易损伤样品,而且透射能力低,很难透过物镜。人们想到了使用高能电子束代替光束,比如 200 keV 的电子对应的的布罗意波长为 0.0025 纳米 (2.5 * 米)。虽然 NA 相对较小(
米)。虽然 NA 相对较小( 约为10°),依然可以达到0.1 纳米的理论分辨率。这就是电子显微镜的基本原理。
约为10°),依然可以达到0.1 纳米的理论分辨率。这就是电子显微镜的基本原理。
严格的说,电镜的分辨率依然限制在光学衍射极限的范围内。只不过这里的“光学”是“电子光学”。
(2) 物方折射率 n
空气折射率为 1,水的折射率 1.33,玻璃折射率 1.58。目前主要的物镜都是玻璃材质,并在物镜与样品之间用与玻璃折射率一致的油来浸润,以提高分辨率。
2012 年 Olympus 发布了一款 NA 高达 1.7 的物镜,光学部分使用蓝宝石(折射率约 1.76)制作,并搭配高折射率的镜油(目测成分应该是二碘甲烷 Methylene iodide)。
也许在未来能发明比玻璃更好的材料,折射率更高、易于制作透镜、并且能找到高折射率的油,这样就能进一步提高分辨率。
比如用钻石(折射率大约2.42)打造一枚土豪物镜,并找到同样折射率的透明液体,分辨率可以提高到 1.5 倍。当然,由于成本及工艺因素,目前尚不现实。
(3) 孔径角
看起来 的最大值是 90°,但是如果在样品的上下两面都放置物镜,相机同时收集这两个物镜中的光呢?
的最大值是 90°,但是如果在样品的上下两面都放置物镜,相机同时收集这两个物镜中的光呢?
这种方法就是 Stephen Hell 在 1991 年发明的 4 Pi 显微技术。此时衍射极限的公式稍有变化,分辨率能提高一倍。
简单理解,限制分辨率的一个原因是从物体上向四面八方发射的光线在经过透镜时,由于透镜大小(孔径)的限制,所以很多光线没有经过物体,其承载的物体的“信息”丢失了。而 4 Pi 其实是通过两个物镜收集了更多的光及“信息”。每个高 NA 的物镜离物体都非常近,所以几乎能收集到各个角度的光,这也是 4 Pi 这个名称的来历——一个以物体为球心的球体其立体角的大小就是 。
。
另一种“结构照明显微技术(SIM)”很聪明地通过类似摩尔纹的原理,获取到更多“信息”,也可以将分辨率提高一倍。解释原理需要用到傅里叶光学,在此就不详述了。它由已故的 Mats Gustafsson 教授于 2000 年发明。
那么问题来了,是否还有办法“真正”突破衍射极限,使之并不受限于这个公式呢?
3. 突破光学衍射极限
前面的公式推导过程中,有两个隐含条件。
第一个隐含条件是需要用到夫琅禾费衍射,而它也是有条件的,它要求物体与像平面之间的距离远远大于光的波长。这个条件称为远场条件。如果离物体足够近,衍射极限便不遵循上述公式。研究波长以内光传播特性的领域叫近场光学。
Eric Betzig 在 1986 年发明的近场扫描光学显微技术(NSOM)就是使用距离物体远小于波长的光学探针来扫描物体,以达到超分辨的显微图像。
4. 单分子荧光与分辨率革命(revolution of resolution)
另一个条件则非常之隐蔽,但却十分朴素,以至于自阿贝推算出衍射极限公式之后的 100 多年间,没有人能够发现或重视。
Stefan Hell 与 Eric Betzig 的贡献就在于解锁了这个隐藏关卡,在固定的波长与 NA 之下,将显微镜的理论分辨能力提高到无限大,带来了 1990 年代以来的分辨率革命。而这次革命非常依赖于 William Moerner 推动的单分子荧光成像等研究,也是为什么本次诺奖会颁发给几乎没做过超分辨显微技术的 William Moerner、颁发给理综奖的原因。
这里要简单插播一下荧光成像的原理:荧光分子(如获得 2008 年的诺贝尔理综奖的绿色荧光蛋白 GFP)在吸收一个高能量的短波长(如蓝光,称为激发光)跃迁到高能态之后,很快会发射一个低能量的长波长(如绿光,称为发射光)光子回到基态能级。
所以我们可以用蓝光照射样品上标记的 GFP,而接收其发射的绿光,来对物体进行成像。这样的一个好处就是图像对比度会非常高,只有带有 GFP 的部位会被成像,其它部位都是暗的。
而每个荧光分子的发光是完全独立的。
回到前面说的第二个隐藏条件,说穿了其实非常简单。推导时假定了图 1 中的物体上的两点 P、Q 同时发光,所以二者的衍射斑才会叠加在一起导致难以区分。但如果 P、Q 是在不同的时间分别发光,那么可以(通过点扩散函数拟合或者去卷积的方法)精确地定位到每个衍射斑的中心点位置 P'、Q'。那么也就不存在这样的衍射极限了,理论上即使 P、Q 相距再近都可以被分别定位而加以区分。
更进一步,广义地来说,只要是 P、Q 两点处在可以探测到的不同“状态”或是不同特征,那么就可以超越衍射极限。分辨率并不仅仅是关于波的,而且是关于“状态”的!
意识到了这一点,很多种真正突破衍射极限的显微技术就被解锁了。比如:
(1) 区分荧光分子的不同构象/能态
荧光分子处在不同构象或能态时,可以发射不同波长的光子,或者不发光。
受激发射耗损显微术(STED):激发光周围套上一圈耗损光,使中心区域的荧光分子处于激发态发光,周围的分子处于耗损态不发光。这样可以使图 1 中的同心圆表示的衍射斑变小,以此来区分两个相距在衍射极限以内的分子。这个方法由 Stefan Hell 在 1994 年发明。
随机光学重构显微术(STORM)、光活化定位显微术(PALM)、荧光活化定位显微术(fPALM):它们的共同特征是使样品中每次仅有少量随机、离散的单个荧光分子发光,通过拟合,找出每个荧光分子中心点的位置。重复拍摄多张图片之后,就可以把所有荧光分子的中心点位置叠加起来形成整幅图像。这些技术由庄小威、Eric Betzig 等人在 2006 分别独立发明。

图 2. 庄小威发明的 STORM 超分辨光学成像效果图。a, b 为传统光学显微镜拍摄,c, d 为相同区域经 STORM 技术拍摄并重构。b, d 为 a, c 的局部放大。图中的结构是细胞内的支架——微管蛋白。图片来自 Nikon MicroscopyU 。
RESOLFT:由于 STED 中,耗损光需要很强的亮度,激光器造价昂贵,而且对样品损伤较大,如果借鉴 STORM/PALM/fPALM 的原理,不需要使周围分子处于“耗损态”,而是采用类似于 STORM 等的特殊荧光分子,用较弱的光强使其处于其它能态,也可以实现超分辨。这也是 Stefan Hell 发明的。
(2) 荧光分子闪烁的不同周期
SOFI:有些荧光分子在持续的激发光照射下,并不是持续发光,而是会闪烁。由于每个荧光分子随机闪烁的时间不一样,可以通过连续拍摄一段录像,分析比较图像中每个像素点记录到的荧光强度在这段时间内的闪烁情况,来区分不同的荧光分子,实现超分辨。2009 年发明。
(3) 荧光分子的极性/朝向不同
SPoD/ExPAN:荧光分子都是偶极子,可以理解成有着不同的朝向。当用不同朝向的偏振光激发时,荧光分子的亮度也会随之不同。可以周期性地改变偏振光朝向,连续拍摄一段录像,分析比较图像中每个像素点荧光强度的周期变化情况,来区分不同荧光分子,实现超分辨。2014 年发明。
……
这些不同的方法,也都有着各自分辨率的计算公式。STED/RESOLFT 的理论分辨率与激发光、耗损光强度有关;STORM/PALM 与单个荧光分子发射的光子数有光;SOFI/SPoD 与相机的像素尺寸有关(采样定理决定)。在固定的波长、NA 下,理论上的分辨率依然可以达到任意高。
如果还能想到荧光分子的更多特性并加以利用,未来还会有越来越多的超分辨显微术被发明。
所以可以看到,William Moerner 开创的单分子荧光成像在超分辨成像中的作用。Stefan Hell、Eric Betzig 使用物理方法利用了荧光分子的化学特性而发明的超分辨显微成像,目前在生物学领域已经得到了广泛应用,因此,给三人颁发一个诺贝尔理综奖也是名至实归的。
------------------------
有兴趣了解超分辨实现方法细节的同学,推荐 @Hydro Ding 的这篇回答,比我写的清楚:光学显微镜受光线的波长限制只能够放大两千倍左右的极限,有办法解决么?或者这就是自然定律的一种界限表现? 显示全部
------------------------------------------------
2014 年的诺贝尔理综奖颁发给了“超分辨荧光显微技术”。也许接下来的几天,媒体会关注 Stefan Hell、Eric Betzig 二人的传奇经历,或者另一名华人女科学家与该奖项失之交臂的遗憾。但是八卦之外,这项成果背后的科学本身也非常有意思。
这里面有三个关键词:“超分辨”、“荧光”和“显微技术”,我希望能够解释清楚以下几个问题,尤其是后两个问题:
1. 为什么需要(光学)显微技术?
2. 为什么光学显微镜的分辨率存在理论极限?
3. 用怎样的方法可以突破这个理论极限以达到“超分辨”?为什么这个理论极限可以被突破?
4. 为什么非得是荧光显微技术,而非普通的明场(透射光)显微技术?
1. 采样定理与显微镜
我们用肉眼观察或者用相机拍摄一个物体时,物体上的每一个细微的点都会在眼睛的视网膜或是相机的感光芯片上成像。那么我们为什么不能看到细菌等微小的东西,为什么不能把照片无限放大以看清远处树木上面的每一片叶子呢?
这个问题的答案比较简单:因为组成视网膜的每一个感光细胞(视杆细胞和视锥细胞)、相机芯片上的每一个感光元件(CCD、CMOS等)都是有大小的。比如视网膜中央凹区域的视锥细胞直径平均约为 5 微米。而由于奈奎斯特-香农采样定理的限制,视网膜上能分清的两个相邻像点的距离是视锥细胞直径的两倍,即 10 微米。再结合眼球的构造,大致可以推断出,在距离眼睛 25 厘米的位置,我们能分辨物体上相距为 80 微米的两个点,换算成点阵密度就是大约 320 ppi,这也是苹果所谓“视网膜屏”分辨率的来历。
如果要观察小于 80 微米的物体,比如细菌,就需要先将物体放大,再用眼睛或者相机观察。现代光学显微镜的构造其实非常简单,样品放置在物镜的焦点处,从样品上发射或散射的光经过物镜变成平行(准直)光,再经过一个结像透镜,然后会聚到相机的感光芯片上成像。
按照前面的方法来推算,要区分物体上相距为 200 纳米的两个点,如果使用科研级相机,比如最近火起来的 sCMOS 相机(每个感光像素尺寸为 6.5 微米),只需要使用放大倍率为 65 倍的物镜就足够了。
那么是否可以通过提高物镜的放大倍率来观察低于 200 纳米的物体,比如细胞里面微管呢?
答案是不可以。
2. 光学衍射极限
由于光是一种电磁波,具有衍射和干涉的特性。
 图 1. 光学显微镜简化示意图
图 1. 光学显微镜简化示意图如上面的简图所示,紫色箭头表示的物体 PQ 经过物镜等之后在相机上成像为P'Q'。由于光的衍射,物体上的点如 P、Q,在相机上并不是单独的点,而是一个个有一定大小的斑,被称为夫琅禾费衍射斑(或称艾里斑),如右侧的同心圆所示。那么,当 P'、Q' 相距太近的时候,两个斑会叠加导致难以分辨。这就要求物体上的 P、Q 要相距一定的距离。
1873 年,德国物理学家、卡尔蔡司公司的恩斯特·阿贝(Ernst Abbe)首次推算出衍射导致的分辨率极限。根据瑞利判据——“当一个像斑的中心落到另一个像斑的边缘时,就算这两个像刚好能被分辨”,显微镜能分辨的物体上两点 P、Q 的最小距离 h 为:
这个公式就是光学显微镜的分辨率公式,或称为光学衍射极限。(注意此处的分辨率与通常说的显示器分辨率含义不同)
其中,
摄影领域常用 f/# 或称光圈值来描述镜头,光圈值与数值孔径可以相互换算。对于一枚光圈为 2.0 的镜头来说,数值孔径为 0.25,其分辨能力约 1.2 微米。
目前常用的高倍物镜 NA 最大为1.49,可以算出,对于可见光,比如波长 500 纳米的绿光,显微镜的分辨率约为 200 纳米。所以,即使再提高物镜的放大倍率,也不能提高显微镜的分辨率。
而 200 纳米这个数值也就通常被称作衍射极限。
2.5. 光学衍射极限的动态范围
从上面的公式可以看到,光学衍射极限其实并不是一个具体的数值,如果改变上述公式中的参数,是可以有效提高分辨率的。
(1) 光的波长
可见光波长范围是400~760 nm,如果使用更短波长的光,比如紫外线,理论上可以提高分辨率。但是紫外线能量高,易损伤样品,而且透射能力低,很难透过物镜。人们想到了使用高能电子束代替光束,比如 200 keV 的电子对应的的布罗意波长为 0.0025 纳米 (2.5 *
严格的说,电镜的分辨率依然限制在光学衍射极限的范围内。只不过这里的“光学”是“电子光学”。
(2) 物方折射率 n
空气折射率为 1,水的折射率 1.33,玻璃折射率 1.58。目前主要的物镜都是玻璃材质,并在物镜与样品之间用与玻璃折射率一致的油来浸润,以提高分辨率。
2012 年 Olympus 发布了一款 NA 高达 1.7 的物镜,光学部分使用蓝宝石(折射率约 1.76)制作,并搭配高折射率的镜油(目测成分应该是二碘甲烷 Methylene iodide)。
也许在未来能发明比玻璃更好的材料,折射率更高、易于制作透镜、并且能找到高折射率的油,这样就能进一步提高分辨率。
比如用钻石(折射率大约2.42)打造一枚土豪物镜,并找到同样折射率的透明液体,分辨率可以提高到 1.5 倍。当然,由于成本及工艺因素,目前尚不现实。
(3) 孔径角
看起来
这种方法就是 Stephen Hell 在 1991 年发明的 4 Pi 显微技术。此时衍射极限的公式稍有变化,分辨率能提高一倍。
简单理解,限制分辨率的一个原因是从物体上向四面八方发射的光线在经过透镜时,由于透镜大小(孔径)的限制,所以很多光线没有经过物体,其承载的物体的“信息”丢失了。而 4 Pi 其实是通过两个物镜收集了更多的光及“信息”。每个高 NA 的物镜离物体都非常近,所以几乎能收集到各个角度的光,这也是 4 Pi 这个名称的来历——一个以物体为球心的球体其立体角的大小就是
另一种“结构照明显微技术(SIM)”很聪明地通过类似摩尔纹的原理,获取到更多“信息”,也可以将分辨率提高一倍。解释原理需要用到傅里叶光学,在此就不详述了。它由已故的 Mats Gustafsson 教授于 2000 年发明。
那么问题来了,是否还有办法“真正”突破衍射极限,使之并不受限于这个公式呢?
3. 突破光学衍射极限
前面的公式推导过程中,有两个隐含条件。
第一个隐含条件是需要用到夫琅禾费衍射,而它也是有条件的,它要求物体与像平面之间的距离远远大于光的波长。这个条件称为远场条件。如果离物体足够近,衍射极限便不遵循上述公式。研究波长以内光传播特性的领域叫近场光学。
Eric Betzig 在 1986 年发明的近场扫描光学显微技术(NSOM)就是使用距离物体远小于波长的光学探针来扫描物体,以达到超分辨的显微图像。
4. 单分子荧光与分辨率革命(revolution of resolution)
另一个条件则非常之隐蔽,但却十分朴素,以至于自阿贝推算出衍射极限公式之后的 100 多年间,没有人能够发现或重视。
Stefan Hell 与 Eric Betzig 的贡献就在于解锁了这个隐藏关卡,在固定的波长与 NA 之下,将显微镜的理论分辨能力提高到无限大,带来了 1990 年代以来的分辨率革命。而这次革命非常依赖于 William Moerner 推动的单分子荧光成像等研究,也是为什么本次诺奖会颁发给几乎没做过超分辨显微技术的 William Moerner、颁发给理综奖的原因。
这里要简单插播一下荧光成像的原理:荧光分子(如获得 2008 年的诺贝尔理综奖的绿色荧光蛋白 GFP)在吸收一个高能量的短波长(如蓝光,称为激发光)跃迁到高能态之后,很快会发射一个低能量的长波长(如绿光,称为发射光)光子回到基态能级。
所以我们可以用蓝光照射样品上标记的 GFP,而接收其发射的绿光,来对物体进行成像。这样的一个好处就是图像对比度会非常高,只有带有 GFP 的部位会被成像,其它部位都是暗的。
而每个荧光分子的发光是完全独立的。
回到前面说的第二个隐藏条件,说穿了其实非常简单。推导时假定了图 1 中的物体上的两点 P、Q 同时发光,所以二者的衍射斑才会叠加在一起导致难以区分。但如果 P、Q 是在不同的时间分别发光,那么可以(通过点扩散函数拟合或者去卷积的方法)精确地定位到每个衍射斑的中心点位置 P'、Q'。那么也就不存在这样的衍射极限了,理论上即使 P、Q 相距再近都可以被分别定位而加以区分。
更进一步,广义地来说,只要是 P、Q 两点处在可以探测到的不同“状态”或是不同特征,那么就可以超越衍射极限。分辨率并不仅仅是关于波的,而且是关于“状态”的!
"Resolution is about waves and states." -- by Stefan Hell
意识到了这一点,很多种真正突破衍射极限的显微技术就被解锁了。比如:
(1) 区分荧光分子的不同构象/能态
荧光分子处在不同构象或能态时,可以发射不同波长的光子,或者不发光。
受激发射耗损显微术(STED):激发光周围套上一圈耗损光,使中心区域的荧光分子处于激发态发光,周围的分子处于耗损态不发光。这样可以使图 1 中的同心圆表示的衍射斑变小,以此来区分两个相距在衍射极限以内的分子。这个方法由 Stefan Hell 在 1994 年发明。
随机光学重构显微术(STORM)、光活化定位显微术(PALM)、荧光活化定位显微术(fPALM):它们的共同特征是使样品中每次仅有少量随机、离散的单个荧光分子发光,通过拟合,找出每个荧光分子中心点的位置。重复拍摄多张图片之后,就可以把所有荧光分子的中心点位置叠加起来形成整幅图像。这些技术由庄小威、Eric Betzig 等人在 2006 分别独立发明。

图 2. 庄小威发明的 STORM 超分辨光学成像效果图。a, b 为传统光学显微镜拍摄,c, d 为相同区域经 STORM 技术拍摄并重构。b, d 为 a, c 的局部放大。图中的结构是细胞内的支架——微管蛋白。图片来自 Nikon MicroscopyU 。
RESOLFT:由于 STED 中,耗损光需要很强的亮度,激光器造价昂贵,而且对样品损伤较大,如果借鉴 STORM/PALM/fPALM 的原理,不需要使周围分子处于“耗损态”,而是采用类似于 STORM 等的特殊荧光分子,用较弱的光强使其处于其它能态,也可以实现超分辨。这也是 Stefan Hell 发明的。
(2) 荧光分子闪烁的不同周期
SOFI:有些荧光分子在持续的激发光照射下,并不是持续发光,而是会闪烁。由于每个荧光分子随机闪烁的时间不一样,可以通过连续拍摄一段录像,分析比较图像中每个像素点记录到的荧光强度在这段时间内的闪烁情况,来区分不同的荧光分子,实现超分辨。2009 年发明。
(3) 荧光分子的极性/朝向不同
SPoD/ExPAN:荧光分子都是偶极子,可以理解成有着不同的朝向。当用不同朝向的偏振光激发时,荧光分子的亮度也会随之不同。可以周期性地改变偏振光朝向,连续拍摄一段录像,分析比较图像中每个像素点荧光强度的周期变化情况,来区分不同荧光分子,实现超分辨。2014 年发明。
……
这些不同的方法,也都有着各自分辨率的计算公式。STED/RESOLFT 的理论分辨率与激发光、耗损光强度有关;STORM/PALM 与单个荧光分子发射的光子数有光;SOFI/SPoD 与相机的像素尺寸有关(采样定理决定)。在固定的波长、NA 下,理论上的分辨率依然可以达到任意高。
如果还能想到荧光分子的更多特性并加以利用,未来还会有越来越多的超分辨显微术被发明。
所以可以看到,William Moerner 开创的单分子荧光成像在超分辨成像中的作用。Stefan Hell、Eric Betzig 使用物理方法利用了荧光分子的化学特性而发明的超分辨显微成像,目前在生物学领域已经得到了广泛应用,因此,给三人颁发一个诺贝尔理综奖也是名至实归的。
------------------------
有兴趣了解超分辨实现方法细节的同学,推荐 @Hydro Ding 的这篇回答,比我写的清楚:光学显微镜受光线的波长限制只能够放大两千倍左右的极限,有办法解决么?或者这就是自然定律的一种界限表现? 显示全部


No comments:
Post a Comment