凡是有 electric charge的地方，四周就存在着electric field，即任何 electric charge都在自己周围的空间激发electric field。带电体在电磁场中运动时若能级发生变化，则会辐射electromagnetic field以保持电磁质量不变，存在Maxwell理论中的脱离物体的携带能量的electric field，所以electromagnetic field具有电磁质量，displacement current与传导电流本质上都是电磁质量的传播。Newton本人已经准备接受他的图象中躲藏在光的神秘行为后面的深刻问题。在物理学中因为看出了互不相关的现象之间有相互一致之点而加以类推，结果竟得到很重要的进展。（1）
Coulomb,s law与光子静止引力质量mγ是否为零有密切的关系。mγ是有限的非零值还是等于0，有本质的区别，并且会给物理学带来一系列原则问题。 现代物理理论均以mγ=0为前提。如果mγ≠0，则电动力学的规范不变性被破坏，使电动力学的一些基本性质失去了依据；电荷将不守恒；光子的偏振态有2变为3；黑体辐射公式要修改；会出现真空色散，即不同频率的光波在真空中的传播速度不同，光速不变性原理遭到了质疑。
二、光 的 物 理 本 质
李学生
摘要: 本文首先分析了光子只具有电磁质量，而没有引力质量，分析了场强叠加原理，从根本上解决了狭义相对论中的奇点问题，使Coulomb,s law和狭义相对论的假设的基础更加牢固。关键词：引力质量、电磁质量、光子、电子、场强叠加原理。
（一）光子问题
“法拉第是很熟悉借助于偏振光来研究产生在透明固体中的胁变的方法的。他作了许多实验，希望发现偏振光在通过内部存在着电解导电或介电感应的媒质时所受到的某种作用。然而他并没有能找到任何这种作用，尽管实验是用按照最适宜发现拉力的效应的方式装置起来的－－电力或电流和光线相垂直，并和偏振平面成45度角。法拉第用各种方式改变了实验，但是没有发现由电解电流或静电感应引起的对光的任何作用。
然而他在确立光和磁之间的关系方面却取得了成功，而他作到这一点的那些实验则描述在他的《实验研究》的第十九组中。我们将把法拉第的发现取作我们有关磁的本性的进一步探索的出发点。从而我们将描述一下他所观察到的现象。
然而他在确立光和磁之间的关系方面却取得了成功，而他作到这一点的那些实验则描述在他的《实验研究》的第十九组中。我们将把法拉第的发现取作我们有关磁的本性的进一步探索的出发点。从而我们将描述一下他所观察到的现象。
一条平面偏振的光线从一种透明的抗磁性媒质中通过；当从媒质中出来时，用一个检偏器截断它的路程，以测定它的偏振面。然后加上一个磁力，使透明媒质中的磁力方向和光线的方向相重合。于是光立即重新出现，但是如果把检偏器转过某一角度，光就又被截断。这就表明，磁力的效应就是使偏振面以光线方向为轴而转过一个确定的角度，这个角度为了截断光线而必须使检偏器转过的那个角度来描述。
偏振面转过的角度和下列各量成正比：
偏振面转过的角度和下列各量成正比：
（1）光线在媒质中超过的距离。因此偏振面是从它的原始位置开始而连续变化的。
（2）磁力在光线方向上的分量。
（3）转动角的大小依赖于媒质的种类。当媒质是空气或任何其他气体时，还没有观察到任何的转动。
（2）磁力在光线方向上的分量。
（3）转动角的大小依赖于媒质的种类。当媒质是空气或任何其他气体时，还没有观察到任何的转动。
这三点说法被包括在一个更普遍的叙述中，那就是，旋转角在数值上等于光线从进入媒质的一点到离开媒质的一点的矢势增量乘以一个系数，而对抗磁性媒质来说，这个系数通常是正的。
在抗磁性物质中，偏振面被转向的方向（一般说来）和一个电流的正方向相同，那个电流就是为了产生和实际存在的磁力同方向的磁力而必须绕着光线运行的。
然而外尔代特却发现，在某些铁磁性媒质中，例如在一种高氯化铁在木精或乙醚的浓溶液中，旋转方向却和将会产生磁力的电流运行方向相反。
这就表明，铁磁性物质和抗磁性物质的区别不仅仅起源于“磁导率”在前一事例中大于而在后一事例中小于空气的磁导率，而这两类物体确实性质相反。
一种物质在磁力作用下获得的使光的偏振面发生施转的能力，并不是恰好正比于它的抗磁的或铁磁的磁化率。事实上，抗磁性物质中的旋转为正而铁磁性物质中的旋转为负这一法则。是有例外情况的，因为中性的铬酸钾是抗磁性的，但它却引起负旋转。
也存在另外一些物质，他们不依赖于磁力的施加就能在光线通过物质时使偏振面向左或向右旋转。在某些这种物质中，性质依赖于一个轴，例如在石英的事例中就是如此。在另一些物质中，性质并不依赖于光线在媒质中的方向，例如在松节油、糖溶液等等中就是如此。然而，在所有这些物质中，如果任何一条光线的偏振面在媒质中是像一个右手螺旋那样地扭转的，则当光线沿相反方向通过媒质时偏振面仍将像右手螺旋似的扭转。当把媒质放在光线的路程上时，观察者为了截断光线就必须旋转他的检偏器，而不论光线是从南或从北向他射来，旋转的方向相对于观察者来说都是相同的。当光线的方向反向时，旋转在空间中的方向当然也会反向。但是当旋转是由磁作用引起的时，它在空间中的方向却不论光是向南还是向北传播都是相同的。如果媒质属于正类，则旋转方向总是和产生或将会产生实际的磁场状态的电流的方向相同，而如果媒质属于负类则旋转方向总是和该电流的方向相反。
由此可以推知，如果光线在从北向南通过了媒质以后受到一个镜面的反射而从南向北返回媒质中，则当旋转是由磁作用引起的时，旋转就会加倍。当旋转只依赖于媒质的种类（而不依赖于光线的方向），就像在松节油等等中那样时，光线在被反射而回到媒质中再从媒质中出来时，它的偏振将是入射时在相同的平面上的，第一次通过时的旋转将在第二次通过时被恰好倒了回来。
现象的物质解释带来了相当大的困难。不论是在磁致旋转方向，还是在某些媒质的表现方面，这些困难还几乎不能说已经解决。然而我们可以通过分析已经观察到的事实来给一种解释作些准备。
运动学中的一个众所周知的定理就是，两个振幅相同、振动周期相同、在同一平面上但沿相反方向转运的匀速圆周振动，当合成在一起时是和一个直线振动相等价的。这一振动的周期等于圆周振动的周期，它的振幅等于圆周振动的振幅的两部，它的方向是两个点的连线，那就是在同一圆周上沿不同方向描述圆周运动的两个质点即将相遇的两个点。因此，如果一个圆周运动的周相被加速，则直线振动的方向将沿着圆周运动的方向转过一个等于周相加速度的二分之一的角。
也可以通过直接的光学实验来证明，两条沿相反方向而圆偏振的强度相同的光线，当合并在一起时就变成一条平面偏振的光线，而且，如果其中一条圆偏振光线的周相由于任何原因被加速了，则全光线的偏振平面会转过一个等于周相加速度之一半的角度。
因此我们可以表示偏振面的旋转现象如下：有一条平面偏振光线射在媒质上。这条光线和两条圆偏振光线相等价，其中一条是右手圆偏振的，而另一条是左手圆偏振的（对观察者而言）。通过了媒质以后，光线仍然是平面偏振的，但在两条圆偏振光线中，右手圆偏振的那一条的周相一定是在通过媒质时相对于另一条而被加速了。
换句话说，右手圆偏振的光线曾经完成了更多次数的振动，从而在媒质内部比周期相同的左手圆偏振的光线具有较小的波长。
现象的这种叙述方式是和任何光的学说都无关的，因为虽然我们使用了波长、圆偏振等等的在我们头脑中可能和某种形式的波动学说相联系的术语，但是推理过程却和这种联系无关而只依赖于被实验证明了的事实。
其次让我们考虑其中一条光线在某一给定时刻的位形。每时刻的运动都是圆周运动的任何波动，都可以用一个螺纹线或螺旋来代表。如果让螺旋绕着它的轴线旋转而并不发生任何纵向运动，则每一个粒子都会描述一个圆，而与此同时，波动的传播则将由螺旋纹路上位置相似的各部分的表现纵向运动来代表。很容易看到，如果螺旋是右手的，而观察者是位于波动所传向的一端的，则在他看来螺旋的运动将显得是左手的，也就是说，运动将显得是逆时针的。因此，这样的一条光线曾经被称为一条左手圆偏振的光线；这名称最初起源于一些法国作者，现在已经在整个的科学界都通行了。
一条右手圆偏振的光线可以按相似的方式用一个左手螺旋来表示。右侧的右手螺旋线A表示一条左手圆偏振的光线，而左侧的左手螺旋线B则表示一条右手圆偏振的光线。
现在让我们考虑在媒质内部具有相同波长的两条这样的光线。他们在一切方面都是几何地相似的，只除了其中一条是另一条的“反演”，即有如另一条在镜子里的像一样。然而，其中一条，譬如说是A，却比另一条具有较短的旋转周期。如果运动完全起源于由位移所引起的力，那么这就表明，当位形像A那样时，由相同的位移引起的力要比位形像B那样时大一些。因此，在这一事例中，左手光线将相对于右手光线而被加速，而且不论各光线是从北向南还是从南向北行进，情况都将是这样的。
因此这就是松节油等等引起的那种现象的解释。在这些媒质中，当位形像A那样时，由一条圆偏振光线所造成的位移将比位形像B那样时引起较大的恢复力。于是这些力就只依赖于位形，而不依赖于运动的方向。”
“但是，各物体的性质是可以定量地测量的。因此我们就得到媒质的数据，例如一种扰动通过媒质而传播的那一速度的数值，而这一速度是可以根据电磁实验来算出的，也是在光的事例中可以直接观测的。如果居然发现电磁扰动的传播速度和光的速度相同，而且这不但在空气中是如此，在别的透明媒质中也是如此，则我们将有很强的理由相信光是一种电磁现象，而且光学资料和电学资料的组合也将产生一种关于媒质之实在性的信念，和我们在其他种类的物质的事例中通过感官资料的组合而得到那种信念相似。”[见《电磁通论》第二十章，光的电磁学说的第三自然段。]
“但是，各物体的性质是可以定量地测量的。因此我们就得到媒质的数据，例如一种扰动通过媒质而传播的那一速度的数值，而这一速度是可以根据电磁实验来算出的，也是在光的事例中可以直接观测的。如果居然发现电磁扰动的传播速度和光的速度相同，而且这不但在空气中是如此，在别的透明媒质中也是如此，则我们将有很强的理由相信光是一种电磁现象，而且光学资料和电学资料的组合也将产生一种关于媒质之实在性的信念，和我们在其他种类的物质的事例中通过感官资料的组合而得到那种信念相似。”[见《电磁通论》第二十章，光的电磁学说的第三自然段。]
凡是有 electric charge的地方，四周就存在着electric field，即任何 electric charge都在自己周围的空间激发electric field。带电体在电磁场中运动时若能级发生变化，则会辐射electromagnetic field以保持电磁质量不变，存在Maxwell理论中的脱离物体的携带能量的electric field，所以electromagnetic field具有电磁质量，displacement current与传导电流本质上都是电磁质量的传播。Newton本人已经准备接受他的图象中躲藏在光的神秘行为后面的深刻问题。在物理学中因为看出了互不相关的现象之间有相互一致之点而加以类推，结果竟得到很重要的进展。（1）
Coulomb,s law与光子静止引力质量mγ是否为零有密切的关系。mγ是有限的非零值还是等于0，有本质的区别，并且会给物理学带来一系列原则问题。 现代物理理论均以mγ=0为前提。如果mγ≠0，则电动力学的规范不变性被破坏，使电动力学的一些基本性质失去了依据；电荷将不守恒；光子的偏振态有2变为3；黑体辐射公式要修改；会出现真空色散，即不同频率的光波在真空中的传播速度不同，光速不变性原理遭到了质疑。
如果mγ≠0，则电磁力为非长程力，Coulomb,s law应有偏差，即f∝r-2±δ，δ≠0；反之，如果mγ=0，则δ=0。因此mγ与Coulomb,s law偏离平方的修正数有关。1930年，Proca指出，如果mγ≠0，则真空中的Maxwell方程组应修改为
式中A和φ分别是电磁场的矢势和标势，c是真空中的光速, h是普朗克常量。②式称为Proca方程，采用的是高斯单位制。Proca方程的解的形式为
当mr≠0时， μ≠0，可见Proca方程的解比通常的Maxwell方程的解多了一个指数因子
。当mr=0时， μ=0，Proca方程回复到Maxwell方程。有
的关系。再利用1971年William等人的实验结果
下限的方法。它使我们再次认识到精确验证电力平方反比律，即确定δ下限的重要性。描写电磁相互作用的局域规范理论称为阿贝尔规范场理论。
。当mr=0时， μ=0，Proca方程回复到Maxwell方程。有的关系。再利用1971年William等人的实验结果下限的方法。它使我们再次认识到精确验证电力平方反比律，即确定δ下限的重要性。描写电磁相互作用的局域规范理论称为阿贝尔规范场理论。
现代物理实验用天体物理的磁压法得出的mγ的最强限制为mγ＜10-60克，既不能否定也不能肯定光子有引力静止质量。弱相互作用存在于除光子外所有基本粒子之间的一种短程作用。光子不参与引力相互作用，而参与电磁相互作用，存在于一切带电粒子或具有磁矩粒子间的电磁相互作用过程中，说明光子的引力静止质量为0，能量由电磁质量携带，这样便避免了狭义相对论中光子的奇点问题，光子能量 hν=m电磁c2，光子的电磁动量为m电磁c。现代物理学认为光子不带电荷是错误的，只是其电荷的电量非常小，现代物理学的实验观察不到，笔者认为当光的强度达到一定程度时，在实验中一定能够观察到。引力质量运动的速度极限是光速，原因在于达到光速时引力质量为无穷大，不可能再加速。各种观察和试验表明，光子的稳定时间至少在103年（因为电磁质量没有时间轴，所以稳定时间为无穷大），这也说明了上面观点的正确性。由于光子的衰变是根据Heisenberg的测不准原理得到，因此测不准原理具有一定的局限性。由于光只具有电磁质量，与绝对时空——引力质量没有相互作用，因此不能把电磁扰动看成ether介质的扰动，光波没有纵波，也不存在ether的切变模量极其大。物体在空间运动自如，得不出ether的密度极其小。由于光只具有电磁质量，因此光是electromagnetic field的一种，光学是电磁学的一个分支，Maxwell的观点是正确的。引力红移的本质在于是引力场强的地方时钟运动慢，在引力场中观察光子的频率减小，与光子是否具有引力质量无关。在阿贝尔规范场理论中，电磁场称为规范场，它的量子，即光子，成为规范粒子。带电粒子间的相互作用是通过交换规范粒子来实现的。Maxwell方程描写了在物质场（通过电流）的作用下电磁场的运动规律，而局域规范不变的狄拉克方程描写了在电磁场作用下物质场的运动规律。两个方程在局域规范变换下都保持不变。利用阿贝尔局域规范不变性，可以唯一地确定满足各种运动方程的带电粒子与电磁场的相互作用形式。它的正确性已得到实验的检验。注意到规范粒子的质量项m2AμAμ不满足局域规范不变性，因此在严格规范不变的局域规范场理论中，规范粒子一定是零引力质量，只具有电磁质量。根据新南威尔士大学天文学家约翰.韦伯收集到的有关数据，一个距地球120亿光年的类星体发出的光，在到达地球的过程中从星云中吸收了错误类型的光子，但是根据现代物理的理论，它是不可能吸收这种类型的光子的。悉尼麦加里大学的理论物理学家戴维斯认为，造成这种现象的原因可能有两个方面：电子的电荷发生了变化或者光速不恒定，笔者认为电子在到达地球的过程中由于辐射了光子，中间电荷发生了变化，因此从星云中吸收了错误类型的光子，进一步说明了光子具有电磁质量。根据现代的光学理论，在入射点处，即使是全反射，在折射律的介质中也有电磁场的存在，不过是以exp(-2izβ/λ)的形式衰减。1959年，庞德与瑞布卡在哈佛塔做了一个著名的实验。他们把发射14.4kev伽玛光子的57钴(Co)放射源放在塔顶，而在塔底测量它射来的伽玛光子频率γ′，比较它与原频率γ的差别。他们的测量结果是
这表明，光子在光传播媒介物质中表现出来的振动频率是由光子具有的绝对能量决定。
历史上对彗尾的尾巴现象解释首先是光压说，但是近代物理学家发现光根本不具有如此威力，甚至光是否存在压力都受到了人们的怀疑，军事专家的观点更支持我们，《军事学教程》中言：“激光武器的特点：不产生后坐力，是一种无惯性武器。”近代实验也发现原子核向外发射出能量极高的 Y 光子时并不做反冲运动（近代理论认为能量越大的光子其动量越大）。我们应该怀疑麦克斯伟所预言的光压了。经典物理后来又转用太阳风来解释彗尾，但目前的研究发现，地球外的宇宙射线是各向同性的，来源于太阳方向上是宇宙射线并不比其他方向上是多，而且宇宙射线来源于那里至今仍是个迷，后来人们发现宇宙射线中有一些“低能质子”的多少与太阳黑子活动存在某种联系，于是认为“低能质子”就是太阳风，但仍然存在两个困难，一是“低能质子”也是各向同性的，二是我们还不清楚是“低能质子”的变化引起太阳黑子活动呢还是太阳黑子活动引起“低能质子”的变化。
彗尾形成的原因很简单，它就是一个早已被人们公认的事实：彗尾是带电的。即彗尾的部分物质——电场——只有电磁质量而无引力质量，万有引力不能吸引这部分质量，因此整个彗尾相对于太阳的加速度是由太阳对彗尾的引力及彗核对彗尾的引力（彗尾的重力）两者的合力提供的。
由于时空是弯曲的，光子是自由粒子，其运动轨迹是测地线——物体总是沿着四维空间——时间的直线走，与光子有无引力质量无关，因此光线弯曲是自然的，光线在天体附近的弯曲是由于引力质量引起空间的弯曲，进一步验证了广义相对论的正确。费马原理应当是这一现象的表现形式，根据最小作用原理，此时的总阻力最小为0。Cassini飞船在其飞向土星的旅程中，它的轨道被太阳所偏转的状态已被测控的无线电波所测定，这又一次证实了Einstein广义相对论中关于时空结构的论断。现在意大利位于三地（Pavia,Rome,Bologna)的三所大学以Berotti为首的科学家们，细致地核对了由Cassini飞船发回的无线电数据，并发现光波轨道的偏转完全符合广义相对论的规范理论。同时他们宣称，他们的测量仪器已达到非常灵敏的程度，可为其他引力模型提供精确的测试。（2）
由于光子不具有引力质量，因此光子时空属性，它在绝对时空中静止，在相对时空中以光速运动。
,偶尔也会转化为三个光子，一对几乎静止的正负电子，其总能量为2mc2。由于动量守恒的要求，两个光子必定以相同的能量朝相反的方向辐射出来。因此每个光子的能量为mc2=0.51Mev,其实它仅为电子的引力能量转化为电磁能量，正负 electric charge中和电磁质量空间量子形式消失，它们激发的electric field的空间结构相互抵消。根据bootstrap关系，所有的基本粒子都是至少由两个基本粒子复合而成的，而且它们之间的关系是可逆的，其中没有哪一种粒子比其他粒子更优越。就是说，任何一种基本粒子都能够充当构成多种其他基本粒子的要素。 当π0介子衰变为两个光子时，由于光子的引力静止质量为0， 因此π0介子内部蕴藏的全部引力能量被释放出来而转变为光子的电磁质量的空间量子 形式。在适当条件下，它们还可以从激发时空中获得，例如正负电子对的产生。Newton讲：“物体变为光和光变为物体是符合自然进程的，自然界似乎以转化为乐”。
,偶尔也会转化为三个光子，一对几乎静止的正负电子，其总能量为2mc2。由于动量守恒的要求，两个光子必定以相同的能量朝相反的方向辐射出来。因此每个光子的能量为mc2=0.51Mev,其实它仅为电子的引力能量转化为电磁能量，正负 electric charge中和电磁质量空间量子形式消失，它们激发的electric field的空间结构相互抵消。根据bootstrap关系，所有的基本粒子都是至少由两个基本粒子复合而成的，而且它们之间的关系是可逆的，其中没有哪一种粒子比其他粒子更优越。就是说，任何一种基本粒子都能够充当构成多种其他基本粒子的要素。 当π0介子衰变为两个光子时，由于光子的引力静止质量为0， 因此π0介子内部蕴藏的全部引力能量被释放出来而转变为光子的电磁质量的空间量子 形式。在适当条件下，它们还可以从激发时空中获得，例如正负电子对的产生。Newton讲：“物体变为光和光变为物体是符合自然进程的，自然界似乎以转化为乐”。
在各种粒子的相互作用中，动量守恒定律依然成立，Compton效应与此理论并不矛盾。在光电效应中由于电子的电磁质量具有量子性，所以只有吸收一定频率的光子电子才能逸出。若频率小于该频率，也不能吸收多个光子使电子逸出，因为电子吸收一个光子后电磁能不在其量子态，这一现象用现代物理学理论无法解释。电子吸收光子后电磁质量增加，能级增大。如果频率进一步增大，多余的电磁能将转化为引力能，使电子具有一定的动能。
光子与电子的特性比较：
注1：根据上面的观点，有效引力质量为0，存在有效电磁质量；
注2：根据上面的观点，存在库仑力，但是非常小。
注3：根据上面的观点，电量不等于0，但是非常小。
注2：根据上面的观点，存在库仑力，但是非常小。
注3：根据上面的观点，电量不等于0，但是非常小。
光子与电子的一个重要区别：光子的数目在传播中不守恒。在吸收介质中光子的数目会减少，而在增益介质（反转介质）中则增加。如果囚禁在反转介质中的光子获得的增益大雨损耗，就可能产生激光。原子核外的电子在核外运动没有确定的轨道的原因之一就是电子吸收光子的频率大于某一能级的电磁能时，其中部分电磁能转化为引力能，动能增加导致运动半径增加，另外时空也是能量存在的方式，电子与时空量子以及其它原子、电子的作用也有关。因此宏观物体的运动与微观粒子的运动遵循同样的规律，微观粒子遵循统计规律是因为作用力复杂难以运用宏观物体的运动规律描述，“薛定谔猫佯谬”不存在。Heisenberg认为：“我相信自然规律的简单性具有一种客观的特征。如果自然界引向极其简单而美丽的数学形式，引向前人所未见过的形式，我们就不得不认为这些形式是真的，认为它们是显示自然界的真正特征。” 在 Einstein那里，大自然的和谐、统一这种美感，已经上升为一种坚定的信念，这给他带来了无穷无尽的探索的力量和智慧。
（二）场 强 叠 加 原 理 的 解 释
靴袢理论认为：在两个强子的相互作用中，没有任何粒子表现为单独负责传递这种作用。参加强相互作用的粒子既可以作初、末态粒子，又可以作为负责引起相互作用的被交换粒子。这一事实对描述这类反应的散射振幅提供了自恰性约束，并且强子是互为组成部分的。这种相互嵌合的粒子体系是通过“自恰性原理”而组成动力学系统的。事实上物质世界是不能归结为最基本的实体的，所谓“基本粒子”只是一组向外散射着的 关系，每一个粒子的行为是由所有其他粒子的行为决定的。因此，其性质可由其他粒子的性质推导出来。物质世界没有“部分”，只有性质。现代物理学已经把强相互作用与电磁作用统一起来，根据上面的观点电磁作用与强相互作用是互为反作用力，所以电磁作用也满足靴袢理论。力其实就是信息的最原始的表现形式。这样不难理解， electric charge跃迁的能级不同，辐射的光子频率不同。
因为electric field是物质存在的一种形态，它有特定的运动规律和物质属性，它和其它带电物质以一定形式发生相互作用，electric field由光子组成，所以 光子具有电磁质量，它的能量可以用hν表示，频率与波长为定值，相当于带有 electric charge。由于 electric charge的电磁质量有正负之分，因此光子的电磁质量也有正负之分，即正负 electric charge辐射的光子应该不同，光子的频率也应当存在正负，这样就可以解释光子发射的原因，自然界不存在静止的光子。量子场论 需要把场论分解成正频和负频两部分。前者沿时间前进方向传播，而后者向后传播。由于正 electric charge与负 electric charge都是能量存在的方式，因此正 electric charge激发或者辐射的光子为负光子，负 electric charge激发或者辐射的光子为正光子，electric field可以脱离 electric charge而独立存在， electric charge的电磁质量与electric field的能量应当相互影响。
根据QED理论，电磁力解释为光子的交换。两个 electric charge位于距离为r的A、B两点，由静止开始作加速运动，两个 electric charge分别辐射以保持电磁质量不变，由于做加速运动，产生引力场，空间曲率变大，引力质量增加，引力能量增加。根据能量最低原理可知，异种 electric charge互相吸引，同种 electric charge互相排斥。正 electric charge在负 electric charge形成的electric field中加速运动，能级增加，辐射electromagnetic field；反之依然。减速运动时，能级降低，应该吸收electromagnetic field以保持电磁质量不变。正光子与负光子互为反粒子，所以同种 electric charge形成的electric field 加强，异种 electric charge形成的electricfield减弱，把 electric charge的相互作用归结光子的相互作用，这也符合靴袢理论。笔者认为能量最低原理可能是自然界的一个基本规律，例如普氏耗散结构的建立，使人们对自然界产生了一种新的认识，这就是当一个系统处于平衡态附近时，其发展过程主要表现为趋向平衡并伴随着熵增加（即无序度的增加——能量最低状态）和结构的破坏。可是当系统在远离平衡的条件下，如果系统是开放的且又与外界有能量、物质的交换，其发展过程可以经过突变而产生新结构并达到新的有序状态——能量最低状态。
光子是组成electric field的基本粒子，具有电磁质量，相当于带有 electric charge，但是quantity of electricity极小，例如γ光子的电磁质量仅相当于电子的电磁质量的2.04×1022分之一，因此在electric field中观察不到光子的电磁质量，与现代物理学的实验并不矛盾，但是高频率的光子在强electric field中运动光线应当弯曲，这一现象可以运用实验验证。宇宙线是由高空射来的带电高能粒子流，其能量的数量级为103——105MeV ，说明当能量达到一定的数量级时(因为此时高能粒子多），它的带电性才显现出来。electric field可以脱离 electric charge而独立存在，那么一个 electric charge产生的electric field应当对它本身有影响，这可能是带电体的运动速度小于1的原因，例如虽然光子与电子相似，但是光子速度为定值，电子速度可变。
参考文献：1、《物理学的进化》Einstein和英费尔德 著 周肇威译 上海科学技术出版社 1962年
2、《物理》第32卷12期89页 2003年 北京
相对论与黎曼几何-11-等效原理
精选
参考文献：1、《物理学的进化》Einstein和英费尔德 著 周肇威译 上海科学技术出版社 1962年
2、《物理》第32卷12期89页 2003年 北京
相对论与黎曼几何-11-等效原理
精选
|||
11. 等效原理
根据狭义相对论，时间和空间不再是独立而绝对的，闵可夫斯基的四维时空将它们联系在一起。在这个理论框架里，所有相对作匀速运动的惯性参考系都是平权的，物理定律在任何惯性参考系中都具有相同的形式。这点似乎完美地满足了爱因斯坦的相对性观念。但是，仔细想想问题又来了，除了惯性参考系之外，还有非惯性参考系呢，比如说在一个加速参考系中的物理规律，是否也应该与惯性参考系中物理规律形式一致呢？
11. 等效原理 上帝经常和人类开玩笑。他早早地派来一个牛顿，点亮了科学殿堂角上的一个小火把，却让无数多个大门紧锁的房屋，仍然隐藏于深邃的黑暗之中 ... (1650)次阅读|(5)个评论
上帝经常和人类开玩笑。他早早地派来一个牛顿，点亮了科学殿堂角上的一个小火把，却让无数多个大门紧锁的房屋，仍然隐藏于深邃的黑暗之中。牛顿之后将近两百年，人类在其火把的照耀下忙乎了一阵子，看清楚了周围不少景观，将牛顿的物理及数学方面的理论发扬光大，同时也发展了多项技术、掀起了工业革命，正兴致勃勃地试图初建文明社会。然而，上帝总想在人类科学殿堂上玩点儿什么花招。于是，来了个数学家黎曼，他造出了一把精妙绝伦的钥匙，将它交给人类后，年纪轻轻便潇洒地驾鹤西去。可是，谁也不知道这个精美的钥匙有何用途？能开启殿堂中的哪扇大门呢？时光荏苒，又过了半个世纪……
爱因斯坦来到了这个世界，他最感兴趣的事就是探索上帝的思想和意图，想了解上帝到底在开些什么玩笑？玩点什么花招？尽管爱因斯坦小时候不像是个神童，但后来也并非“大器晚成”，他26岁就以研究光电效应和建立狭义相对论而一鸣惊人。
狭义相对论是基于爱因斯坦认为最重要、最具普适性的两个基本原理：相对性原理和光速不变原理而建立的，它用洛伦茨变换，将麦克斯韦的电磁理论，天衣无缝地编织进新的时空理论中。
上帝不应该只是偏爱那些被挑选出来称之为“惯性参考系”的系统吧，况且，哪些参考系就有优先权作为“惯性参考系”呢？既然对惯性参考系而言，速度只有相对的意义，难道还有理由把加速度当作绝对概念吗？爱因斯坦建立了狭义相对论之后，立即意识到这些问题。这种“狭义”的相对性原理，似乎仍然没有真正摆脱“绝对参考系”的困惑，只不过是用了多个“绝对”替代了原来的一个而已。因此，这个“狭义”的概念必须推广。此外，爱因斯坦也经常思考“引力”的问题：如何才能将万有引力也包括到相对论的框架中？
最简单的非惯性参考系是相对惯性系统作直线匀加速运动的参考系。从最基本的原理、最简单的情形出发来思考问题，从来就是爱因斯坦的特点。
科学研究最重要的原动力是什么？不是对功成名就的向往，不是对物质利益的追求，也不是出于对大师前辈的膜拜，或者想要出人头地的愿望。就爱因斯坦而言，最重要的是他对大自然始终保持着的那颗如孩童般纯真的好奇心。不可否认，光电效应的理论探索带给他荣誉；狭义相对论和广义相对论的建立带给他满足，但只有这种始终如一的好奇心，才能支持他后半生持续钻研统一理论四十年如一日终究未成正果却无怨无悔。也许，这才是爱因斯坦“天才”的奥秘所在。
回到非惯性参考系和引力。凡是有一点点物理知识的人，都知道意大利的比萨斜塔，在物理上因为伽利略在那儿做的“自由落体”实验而著名。伽利略的实验证明了，地表引力场中一切自由落体都具有同样的加速度。也就是说，不管你往下丢的是铁球还是木球，都将同时到达地面。后来又有一种看法，说伽利略本人并未做过此斜塔实验，但这点并不重要，斜塔实验所证明的物理规律是公认的。后人进行过多次类似的实验，还不仅仅在地球上，1971年阿波罗15号的宇航员大卫·斯科特，在月球表面上将一把锤子和一根羽毛同时扔出，两样东西同时落“月”之后，他兴奋地对地球上的数万电视观众喊道：“你们知道吗？伽利略先生是正确的！”
无论如何，爱因斯坦先生认识到这条定律的重要性，因为它首先可以被表述为“惯性质量等于引力质量”，继而又进一步地推论到加速度与引力间的等效原理。对此原理，爱因斯坦曾经如是说：
“我为它的存在感到极为惊奇，并且猜想其中必有可以更深入了解惯性和引力的关键。”
何谓惯性质量，又何谓引力质量呢？简言之，牛顿第二定律F=ma中的m是惯性质量，它表征物体的惯性，即抵抗速度变化的能力，而引力质量则是决定作用在物体上引力（如重力）大小的一个参数。在伽利略的自由落体实验中，与引力质量成正比的地球引力，克服惯性质量而引起了物体的加速度。这个加速度应该正比于两个质量的比值。正如实验所证实的，下落加速度对所有物体都一样，那么两个质量的比值也对所有物体都一样。既然对所有物体都相同，两者的比例系数便可以选为1，说明这两个质量实际上是同一个东西。这个看起来平淡无奇的结论却激发了爱因斯塔的好奇心，他认为其中也许深藏着惯性和引力之间的奥秘。
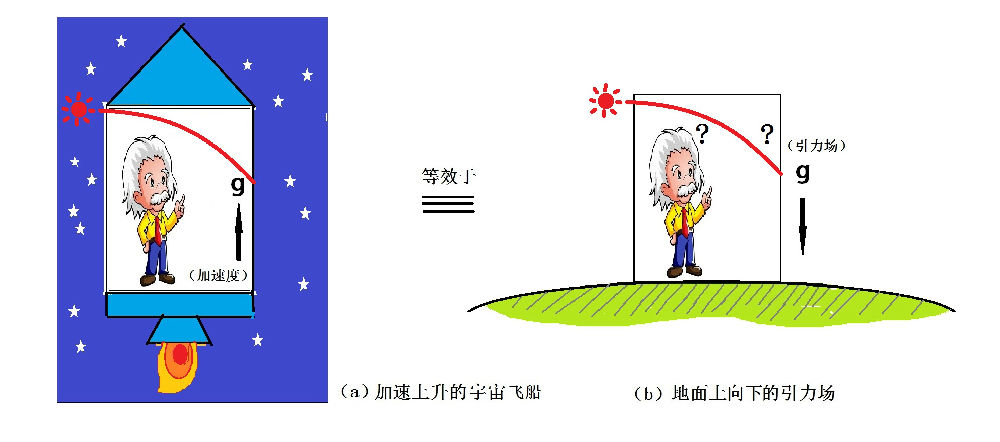
图2-11-1：等效原理
爱因斯坦设计了一个思想实验来探索这个奥秘。下面的说法不见得完全等同于他原来的描述，但实验的基本思想是同样的。如图2-11-1所示，设想在没有重力的宇宙空间中，一个飞船以匀加速度g=9.8m/s2上升。也就是说，飞船的上升加速度与地面上的重力加速度相等。关在飞船中看不到外面的观察者，将会感到一个向下的力。这种效应和我们坐汽车时经历到的一样：如果汽车向前加速的话，车上乘客会感觉一个相反方向（向后）的作用力，反之亦然。因此，图2-11-1的图a和图b中的人，无法区分他是在以匀加速度上升的飞船中，还是在地面的引力场中。换言之，加速度和引力场是等效的。
再进一步考虑如果有光线从外面水平射进宇宙飞船时的情形，如图2-11-1a所示，因为飞船加速向上运动，原来水平方向的光线在到达飞船另一侧时应该射在更低一些的位置。因此，飞船中的观察者看到的光线是一条向下弯曲的抛物线。然后，既然图2-11-1b所示的引力场，是与图a等效的，那么，当光线通过引力场的时候，就也应该和飞船中的光线一样，呈向下弯曲的抛物线形状。也就是说，光线将由于引力的作用而弯曲。
光线在引力场中弯曲的现象也可以从另一个角度来理解，可以认为不是光线弯曲了，而是引力场使得它周围的空间弯曲了。或者更为准确地表达，沿用相对论的术语，是叫做“时空弯曲了”。光线仍然是按照最短的路径传播，只不过在弯曲的时空里的最短路径已经不是原来的直线而已。
从引力与加速度等效这点，还可以推论出另一个惊人的结论：引力可以通过选择一个适当的加速参考系来消除。比如说，一台突然断了缆绳的电梯，立即成为一个自由落体，将会以等于9.8m/s2的重力加速度g下降。在这个电梯中的人，会产生使你感觉极不舒服的“失重感”。不仅仅你自己有失重感觉，你也会看到别的物体没有了重量的现象。也就是说，电梯下落的加速度抵消了地球的引力，这其实是我们在如今的游乐场中经常能体会到的经历。爱因斯坦却从中看出了暗藏的引力奥秘：引力与其它的力（比如电力）大不一样。因为我们不可能用诸如加速度这样的东西来抵消电力！但为什么可以消除引力呢？也许引力根本可以不被当成一种力，就像前面一段所想象的那样，可以将它当成是弯曲时空本来就有的某种性质。这种将引力作为时空某种性质的奇思妙想，将爱因斯坦引向了广义相对论。
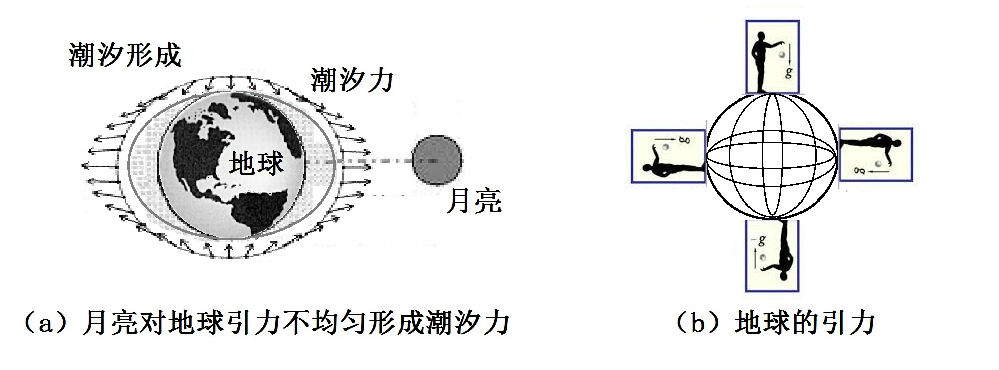
开始的时候，爱因斯坦只是企图按照上面的思路，企图将引力包括到狭义相对论的范畴中。不过，他很快就意识到碰到了大障碍。一个均匀的引力场的确可以等效于一个匀加速度参考系。但是，我们的宇宙中并不存在真正均匀的引力场。根据万有引力定律，引力与离引力源的距离成平方反比率。也就是说，地球施加在我们头顶的力比施加在双脚的力要小一些。并且，引力的方向总是指向引力源的中心。即作用在我们身体右侧和左侧的引力方向并不是完全平行的。我们在地球表面感到“重力处处一样”的现象只是一个近似，是因为我们个人的身体尺寸，比较起地球来说是太小了，我们感觉不到重力在身体不同部位产生的微小差异。然而，爱因斯坦需要建立宇宙中引力的物理数学模型，就必须考虑这点了。在大范围内，这种差异能产生明显的可见效应。比如说，我们所熟知的地球表面海洋的潮汐现象，就是因为月亮对地球的引力不是一个均匀引力场而形成的，见图2-11-2a。
图2-11-2：潮汐力、地球的引力
潮汐力的名词来源于地球上海洋的潮起潮落，但后来在广义相对论中，人们将由于引力不均匀而造成的现象都统称为潮汐力。
尽管“爱因斯坦电梯”的思想实验描述了如何用一个匀加速参考系来抵消一个均匀的引力场，但是实际上的引力场却是非均匀的，不可能使用任何参考系的变换来消除。图2-11-2b显示出地球的引力场，在四个方向需要四个不同的匀加速参考系来局部等效地近似描述。
这个问题困惑了爱因斯坦好几年，直到他后来得到他大学的同窗和好友、数学家格罗斯曼的帮助为止。根据格罗斯曼的介绍，爱因斯坦才惊奇地发现，原来早在半个世纪之前，黎曼等人就已经创造出了他正好需要的数学工具。黎曼几何这把精美的钥匙，就像是为爱因斯坦的理论定做的，有了它，爱因斯坦才顺利地开启了广义相对论的大门。
相对论与黎曼几何-11-等效原理 2014-10-16
- 相对论与黎曼几何-10-测地线和曲率张量 2014-10-09
- 10. 测地线和曲率张量 平行移动的概念不仅可以被用来定义曲面的曲率，也可以被用来定义测地线。 测地线是欧几里德几何中“直线”概念在 ...
- 相对论与黎曼几何-9-平行移动和曲率 2014-09-29
- 9. 二维曲面上的平行移动和曲率 根据上节最后得到的“无限小”平行移动公式，理论上便知道了如何将一个矢量的坐标分量改变使其作平行移动，但在实际 ...
- 相对论与黎曼几何-8-平行移动和协变微分 2014-09-22
- 8. 平行移动和协变微分 什么是平行移动？简单地说，就是将一个矢量平行于自身的方向沿着空间里的一条曲线移动。在平坦的欧几里德空间里，这种移动方 ...
- 相对论与黎曼几何-7-黎曼几何 2014-09-12
- 7. 黎曼几何 在介绍“内蕴几何”一节中说过，高斯以他的“绝妙定理”建立了曲面内在的微分几何。之后，是高斯的得意门生黎曼，将曲面的概念扩展到流 ...
- 相对论与黎曼几何-6-相对论的诞生 2014-09-02
- 6. 爱因斯坦和相对论 据说爱因斯坦在两个星期就建立了狭义相对论，这固然因为他是天才，但也不能不承认当时这个理论已经万事俱备只欠东风、水到渠成 ...
- 相对论与黎曼几何-5-相对性原理 2014-08-23
- 5. 相对性原理 牛顿和爱因斯坦，这是物理学史上的两个丰碑。物理学终究不同于数学，在数学中，欧几里德可以根据五条公理建立欧几里德几何。数学家们 ...
- 相对论与黎曼几何-4-内蕴几何 2014-08-12
- 4. 内蕴几何 高斯在 1827 年的著作《关于曲面的一般研究》中，发展了内蕴几何 【 1 】 。 所谓“内蕴”，是相对于“外嵌”而言。 相对论与黎曼几何-11-等效原理
- 热度 3
- 11. 等效原理 上帝经常和人类开玩笑。他早早地派来一个牛顿，点亮了科学殿堂角上的一个小火把，却让无数多个大门紧锁的房屋，仍然隐藏于深邃的黑暗之中。牛顿之后将近两百年，人类在其火把的照耀下忙乎了一阵子，看清楚了周围不少景观，将牛顿的物理及数学方面的理论发扬光大，同时也发展了多项技术、掀起了工业革 ...
-
- 分享 相对论与黎曼几何-10-测地线和曲率张量
- 热度 4
- 10. 测地线和曲率张量 平行移动的概念不仅可以被用来定义曲面的曲率，也可以被用来定义测地线。 测地线是欧几里德几何中“直线”概念在黎曼几何中的推广。欧氏几何中的直线，整体来说是两点之间最短的连线，局部来说可以用“切矢量方向不改变”来定义它。将后面一条的说法稍加改动，便可以直接推广 ...
- 分享 相对论与黎曼几何-9-平行移动和曲率
- 热度 7
- 9. 二维曲面上的平行移动和曲率 根据上节最后得到的“无限小”平行移动公式，理论上便知道了如何将一个矢量的坐标分量改变使其作平行移动，但在实际情况下往往不是那么容易操作的。因此，首先举几个实际中的简单例子，给二维曲面特殊情形下的平行移动作点直观说明。在这些例子中，我们只感兴趣矢量绕某个闭曲线 ...
- 分享 相对论与黎曼几何-8-平行移动和协变微分
- 热度 6
- 8. 平行移动和协变微分 什么是平行移动？简单地说，就是将一个矢量平行于自身的方向沿着空间里的一条曲线移动。在平坦的欧几里德空间里，这种移动方式似乎是一目了然的。 比如说，让我们想象有一个极小极扁的平面生物“阿扁”，生活在一张平坦的纸上。阿扁会使用坐标系，他对他的世界进行观察和测量 ...
- 分享 相对论与黎曼几何-7-黎曼几何
- 热度 10
- 7. 黎曼几何 在介绍“内蕴几何”一节中说过，高斯以他的“绝妙定理”建立了曲面内在的微分几何。之后，是高斯的得意门生黎曼，将曲面的概念扩展到流形（ Manifolds ），将内蕴几何扩展到 n 维的一般情形，建立了黎曼几何。 和高斯一样，黎曼（ 1826-1866 ）也是德国数学家，同样出生在贫困的普通家 ...
- 分享 相对论与黎曼几何-6-相对论的诞生
- 热度 9
- 6. 爱因斯坦和相对论 据说爱因斯坦在两个星期就建立了狭义相对论，这固然因为他是天才，但也不能不承认当时这个理论已经万事俱备只欠东风、水到渠成呼之欲出的事实。 当年，牛顿力学和麦克斯韦电磁理论各自都取得了巨大成功，但两者似乎不相容。牛顿力学建立在伽利略变换的基础上，对所有的惯性参考 ...
- 分享 相对论与黎曼几何-5-相对性原理
- 热度 6
- 5. 相对性原理 牛顿和爱因斯坦，这是物理学史上的两个丰碑。物理学终究不同于数学，在数学中，欧几里德可以根据五条公理建立欧几里德几何。数学家们将其中的平行共设作些许改变，又建立了双曲几何或球面几何。物理理论的建立却需要以实验观察为基础。实验观察都是在一定的坐标系，或者说一定的“参考系”下面进 ...
- 分享 相对论与黎曼几何-4-内蕴几何
- 热度 7
- 4. 内蕴几何 高斯在 1827 年的著作《关于曲面的一般研究》中，发展了内蕴几何 【 1 】 。 所谓“内蕴”，是相对于“外嵌”而言。指的是曲面（或曲线）不依赖于它在三维空间中嵌入方式的某些性质。“内蕴”的概念也可以被解释得更为物理一些：一个观察者在自己生活的物理空间中所能够观察和测 ...
- 分享 相对论与黎曼几何-3-曲面的微分几何
- 热度 9
- 3. 曲面的微分几何 用微积分的方法对曲线及曲面进行研究，除了欧拉、克莱洛等人的贡献之外，蒙日（ GaspardMonge ， 1746-1818 ）的工作举足轻重。蒙日是画法几何学的创始人，他也对曲线和曲面在三维空间中的相关性质作了详细研究，并于 1805 年出版了第一本系统的微分几何教材：《分析法在几何中的应用》。这 ...
- 分享 相对论与黎曼几何-2-牛顿引力
- 热度 8
- 2. 牛顿 引力 当年， 18 岁的克莱洛因为对空间曲线曲率和挠率的研究而被选入了法国科学院，在那儿，他与皮埃尔·莫佩尔蒂成为了好朋友。莫佩尔蒂比克莱洛大 15 岁，但在当时也算是一名相当年轻的科学院院士。莫佩尔蒂后来因为研究最小作用量原理而知名，我们曾经在第一篇中提到过他在这方面的贡献。那个时代，欧洲的 ...
- 分享
- 《数理同源2》-广义相对论与黎曼几何-1
- 热度 31
- 第二篇 黎曼几何和广义相对论 1. 既古老又现代的几何学 几何是一门古老的学科。恐怕没有哪一门学科，像欧几里德几何学那样，在公元前就已经被创立成形，历经 2000 多年，至今还活跃在许多课堂上和数学竞赛试题中。尽管目前中国的中学教育已经不把平面几何当作必修课，一些学校删减了许多内容或者干 ...
No comments:
Post a Comment