Monday, May 25, 2015

纠缠态是一种最接近经典光场并存在光子数泊松分布的最简单的连续变量态

光学分束器系统作用下的叠加相干态的非经典特性研究- 豆丁网

www.wanlibo.com/p-911446745.html - 轉為繁體網頁
2014年9月9日 - 第三章介绍光场的非经典特性，包括反聚束、压缩等，及纠缠的度量 .... 一方面，相干态是一种最接近经典光场并存在光子数泊松分布的最简单的连续 ...

  • 单模激发纠缠相干态的数学特性- 豆丁网 - docin.com豆丁网

    docin.com.cn/p-723934615.html

    轉為繁體網頁
    2013年11月10日 - 此外，纠缠态是一种最接近经典光场并存在光子数泊松分布的最简单的连续变量态。相干态定义的幅度和相位满足海森堡测不准原理中的最小测不准 ...

  • 激发纠缠相干态的非经典特性研究- 豆丁网 - docin.com豆丁网

    docin.com.cn/p-912049775.html

    轉為繁體網頁
    2014年9月10日 - 一方面，纠缠态是一种最接近经典光场并存在光子数泊松分布的最简单的连续变量态。相干态定义的幅度和相位满足海森堡测不准原理中的最小测不 ...

  • （理论物理专业优秀论文）两模激发纠缠相干态及其纠缠特性研究

    www.doc88.com/p-871103439704.html

    轉為繁體網頁
    2012年5月4日 - ... 处理过程离不开量子态及其演化而量子纠缠态是量子态中的最重要的 ..... 一方面纠缠态是一种最接近经典光场并存在光子数泊松分布的最简单 ...



    • Poisson 分布
    曹亮吉     		 

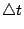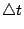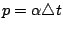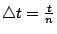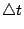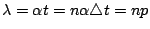      二項分布是離散型機率模型中最有名的一個，其次是 Poisson 分布，它可以看成為二項分布的一種極限情形。 假定某機關的總機在一個短時間 $\triangle t$ 內會接到一次電話的機率 p 與 $\triangle t$ 成正比： $p=\alpha\triangle t$，α 為一常數。又假定在此短時間內接到多於一次電話的機率微乎其微，可以略去不計。那麼在時間 t 內，會接到 x 次電話的機率分布為何？ 我們可以把 t 分成 n 小段，每小段長為 $\triangle t=\frac{t}{n}$。整個問題可看成為：在每個 $\triangle t$ 時間內，我們做了一次試驗，其成功（接到電話）的機率為 p。如此做了 n 次，那麼成功了 x 次的機率為何？所以我們要的機率分布正是二項分布 b(x;n,p)。令 $\lambda = \alpha t = n\alpha\triangle t = np$，則

    \begin{eqnarray*} &&b(x;n,p)\\ &=&\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}\\ &=&\fra... ...}{n})^{-\frac{n}{\lambda}})^{-\lambda}(1-\frac{\lambda}{n})^{-x} \end{eqnarray*}


    當 t 保持不變（亦即 λ 不變），而讓 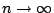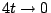$n\rightarrow\infty$ ( $4t \rightarrow 0$)，則

    \begin{eqnarray*} && (1-\frac{1}{n})(1-\frac{2}{n})\cdots(1-\frac{x-1}{n})\right... ...da}}\rightarrow e \\ && (1-\frac{\lambda}{n})^{-x}\rightarrow 1 \end{eqnarray*}


    所以
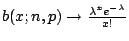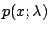    $b(x;n,p)\rightarrow\frac{\lambda^xe^{-\lambda}}{x!}$ （以 $p(x;\lambda)$ 表之，此處的 p 代表 Poisson）
    因為

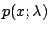    \begin{displaymath} \sum_{x=0}^{\infty}p(x;\lambda)=e^{-\lambda}\sum_{x=0}^{\infty}\frac{\lambda^x}{x!}=e^{-\lambda}e^{\lambda}=1 \end{displaymath}


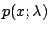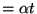    所以 $p(x;\lambda)$ 的確是個機率分布（各種可能的機率之和等於 1）。 這就是說，在時間 t 內，接到 x 次電話的機率為 $p(x;\lambda)$。這是以 λ 為參數的 Poisson 分布，而 λ（$=\alpha t$）是在時間 t 內所期望接到的電話數。 Simeon D. Poisson（1781～1840年）是一個著名的法國數學家及物理學家。到了晚年，他熱衷於將數學的機率論用到司法的運作上。他在這方面的主要著作是1837年出版的《司法機率的研究》(Recherches sur la Probabilité des Jugements)。雖然這本書的主旨是要對司法運作有具體的貢獻，但它包含了許多純粹數學的、機率的理論，所以可以看成是一本以司法應用為例的機率課本，這本書德文版的書名《機率論及其重要應用》(Lehrbuch der Wathrscheinlichkeitsrechnung und deren wichtigstein Auwendungen) 看起來和內容較為一致。在這本書的數學推演中，Poisson 從二項分布的極限得到了這個日後以他為名的機率分布。 Poisson 雖然得到這樣的機率分布，但在書中他並沒有繼續討論這種分布的性質，在往後的研究中，Poisson 似乎也把它忘掉了。 在十九世紀的許多統計研究報告上，Poisson 這個名字經常出現，但這與 Poisson 分布無關，大家所關注的是他在常態分布方面的研究。常態分布在解釋理論與數據變異之間的關係非常成功，當時許多人認為常態分布是機率與統計之間唯一的橋梁了。 直到十九世紀末，Bortkiewicz 才注意到 Poisson 分布與某些數據之間也有類似的關聯。Ladislaus von Bortkiewicz（1868～1931年）是出生在俄國聖彼得堡的波蘭人。他在德國 Göttingen 大學得到學位（1893年），並曾在 Strassburg 做過研究。在 Strassburg 時，他寫了一本小冊子《小數法則》(Das Gesetz der Kleinen Zahlen)，專門研究 Poisson 分布。他不但在理論方面推演了 Poisson 分布的許多性質，並且在應用方面，也比較了一些實際發生的、有關於自殺或意外傷害的數據。Poisson 分布雖然出於 Poisson 之手，但真正使它為人重視，使它成為統計學一部分的可要算是 Bortkiewicz了。 在這本書中，Bortkiewicz 舉了一個至今仍是膾炙人口的例子，說明數據契合 Poisson 分布的情形。從1875到1894年的20年間，德國的十四個軍團部有士兵被馬踢傷因而致死的人數紀錄。這 20×l4 = 280個（團年）紀錄，按死亡人數來分，則如表一的左二欄所示。
    x=每年死亡人數團年數280p(x;0.7)
    0144139.0
    19197.3
    23234.1
    3118.0
    421.4
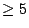    $\geq5$00.2
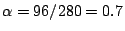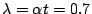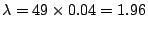    在280個紀錄中，死亡的人數共有196，因此致死率為 $\alpha=96/280=0.7$（人/團年）。我們就以此 α 為 Poisson 分布中的常數，t=1 年，則 $\lambda=\alpha t=0.7$。理想中每團每年死亡人數 x 要遵行 Poisson 分布 p(x;0.7)。表一中右欄就是根據這樣的 Poisson 分布，把280團年該有 x 人死亡的團年數列出。它和表一的中間一欄的數據的確相當吻合。 Poisson 分布既然是二項分布的極限情形，反過來 Poisson 分布也可以做為二項分布的近似值。譬如 p=0.04,n=49，則 $\lambda=49\times 0.04=1.96$。我們把 b(x;49,0.04) 與 p(x;1.96) 之值相對照就得表二
    xb(x;49,0.04)p(x;1.96)
    00.1350.141
    10.2760.276
    20.2760.270
    30.1800.176
    40.0860.086
    50.0320.034
    60.0100.011
    70.0030.003
    80.0010.001
    $\vdots$$\vdots$$\vdots$
    我們發現對應的值相當接近。一般，若用列表方式，則二項分布 b(x;n,p) 要兼顧三個變數 x,n,p，而 Poisson 只要兩個：x,λ，所以較為方便。若直接計算，則因

    b(x;49,0.04)=Cx49(0.04)x(0.96)49-x


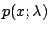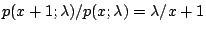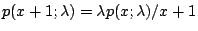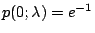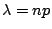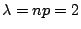    所以二項分布算起來相當費事。另一方面 $p(x;\lambda)$ 之值可用遞迴方法迅速求得： $p(x+1;\lambda)/p(x;\lambda) = \lambda/x+1$ 或 $p(x+1;\lambda) = \lambda p(x;\lambda)/x+1$；而 $p(0;\lambda)=e^{-1}$ 可由指數表中查得。因此只要情況適合，我們當然就捨二項分布而就 Poisson 分布了。 通常只要 n 很大，p 很小，$\lambda=np$ 不大不小而且是個已知定數，Poisson 分布就可以代替二項分布了，譬如某商店每星期進進出出的客人很多（=n），但每個客人買魚子醬的機率很小（=p），只知道平均一星期賣出兩罐：$\lambda=np=2$。那麼這家商店每星期開始時應有幾罐魚子醬的庫存？當然不能只有兩罐，因為平均歸平均，售量超過平均數的機率很大。當然庫存太多也會影響整個商店的運作。根據 Poisson 分布 p(x;2)，我們算得表三：
    λ012345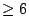$\geq6$
    p(x;2).135.271.271.180.090.036.017
    由表三可知售量達到 5 罐以上的機率只有 5.3%，而達到 6 罐以上則只有 1.7%。所以合理的庫存量為 4 罐（平均19星期才會有一次缺貨），如果怕萬一，那麼 5 罐就非常保險（平均59星期才會有一次缺貨）。 我們從另一個角度來看上面的數據。假設某工廠每做100個螺絲釘，平均會有兩個不合規格，而這是合理的不合格率。根據 Poisson 分布，偶而出現 3 個或 4 個不合規格的螺絲釘也是正常的現象。但是如果出現的頻率太高，或出現 5 個以上的不合規格的螺絲釘，那麼生產過程就可能出了問題。Poisson 分布是品質管制的利器，它可以幫助我們決定生產過程是否出了毛病。 Poisson 分布還有種種的用途：放射性物質的蛻變、細胞間因受 X 光照射而引起的染色體交換次數、細菌和血球的計數、交通事故數及死亡率等等莫不遵行 Poisson 分布。其實，無論在自然科學、在工業、在農業、在商業、在醫藥、在交通、在社會或在軍事上，無不可找到 Poisson 分布的應用。 和二項分布一樣，我們也可以從理論方面來探討 Poisson 分布的期望值 μ 及散布差 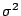$\sigma^2$。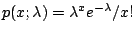由 $p(x;\lambda)=\lambda^xe^{-\lambda}/x!$，我們馬上算得

    \begin{eqnarray*} \mu &=& \sum_{x=0}^{\infty}xp(x;\lambda) = \lambda e^{\lambda... ...lambda) \\ &=& \lambda^2-(2\lambda-1)\lambda+\lambda^2=\lambda \end{eqnarray*}


    所以 Poisson 分布的確是以 λ 為期望值。 在〈二項分布與大數法則〉（《科學月刊》第十六卷第六期）一文中，我們曾導出二項分布的 Chebyshev 不等式

    \begin{displaymath} (\vert\frac{x}{n}-\mu\vert > \epsilon \; \mbox{{\fontfamily{... ...}\selectfont \char 48} } ) \leq \frac{\sigma^2}{n^2\epsilon^2} \end{displaymath}


    如果把二項分布換成 Poisson 分布或任何離散型分布，不等式也照樣成立，因為在導出不等式的過程中只用到 b(x;n,p) 是種機率分布這件事，並沒有用到 b(x;n,p) 之值。現在既然知道 Poisson 分布的 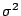$\sigma^2$（=λ）是個（與 n 無關的）定值，所以我們也可以得到關於 Poisson 分布的大數法則：

    \begin{displaymath} \lim_{n\rightarrow\infty}(\vert\frac{x}{n}-\lambda\vert > \e... ....1pt{\fontfamily{cwM7}\fontseries{m}\selectfont \char 48} })=0 \end{displaymath}


    亦即：在 Poisson 分布的機率模型假定之下，只要試驗的次數 n 夠大，則事件發生的次數比 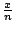$\frac{x}{n}$，從機率的觀點來看，就會很接近期望值 λ。

    前几天，我看到一篇很有趣的文章，使用"泊松分布"（Poisson distribution），判断同一年发生7起枪击案是否巧合。

    让我们先通过一个例子，了解什么是"泊松分布"。

    已知某家小杂货店，平均每周售出2个水果罐头。请问该店水果罐头的最佳库存量是多少？
    假定不存在季节因素，可以近似认为，这个问题满足以下三个条件：
    （1）顾客购买水果罐头是小概率事件。
    （2）购买水果罐头的顾客是独立的，不会互相影响。
    （3）顾客购买水果罐头的概率是稳定的。
    在统计学上，只要某类事件满足上面三个条件，它就服从"泊松分布"。
    泊松分布的公式如下：
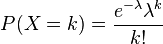
    P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}
    各个参数的含义：
    　　P：每周销售k个罐头的概率。
    　　X：水果罐头的销售变量。
    　　k：X的取值（0，1，2，3...）。
    　　λ：每周水果罐头的平均销售量，是一个常数，本题为2。
    根据公式，计算得到每周销量的分布：

    从上表可见，如果存货4个罐头，95%的概率不会缺货（平均每19周发生一次）；如果存货5个罐头，98%的概率不会缺货（平均59周发生一次）。

    现在，我们再回过头，来看美国枪击案。
    假定它们满足"泊松分布"的三个条件：
    　　（1）枪击案是小概率事件。
    　　（2）枪击案是独立的，不会互相影响。
    　　（3）枪击案的发生概率是稳定的。
    显然，第三个条件是关键。如果成立，就说明美国的治安没有恶化；如果不成立，就说明枪击案的发生概率不稳定，正在提高，美国治安恶化。
    根据资料，1982--2012年枪击案的分布情况如下：

    计算得到，平均每年发生2起枪击案，所以 λ = 2 。

    上图中，蓝色的条形柱是实际的观察值，红色的虚线是理论的预期值。可以看到，观察值与期望值还是相当接近的。

    我们用"卡方检验"（chi-square test），检验观察值与期望值之间是否存在显著差异。
    　　卡方统计量 = Σ [ ( 观察值 - 期望值 ) ^ 2 / 期望值 ]
    计算得到，卡方统计量等于9.82。查表后得到，置信水平0.90、自由度7的卡方分布临界值为12.017。因此，卡方统计量小于临界值，这表明枪击案的观察值与期望值之间没有显著差异。所以，可以接受"发生枪击案的概率是稳定的"假设，也就是说，从统计学上无法得到美国治安正在恶化的结论。
    但是，也必须看到，卡方统计量9.82离临界值很接近，p-value只有0.18。也就是说，对于"美国治安没有恶化"的结论，我们只有82%的把握，还有18%的可能是我们错了，美国治安实际上正在恶化。因此，这就需要看今后两年中，是否还有大量枪击案发生。如果确实发生了，泊松分布就不成立了。
    [参考阅读]
    　　* 泊松分布，by 曹亮吉
    　　* 卡方分布（PDF文件）
    Posted by at

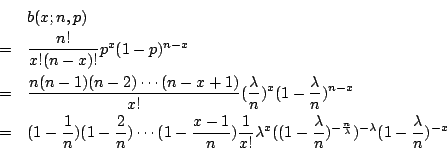
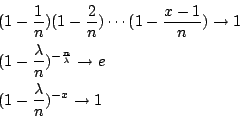
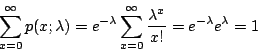
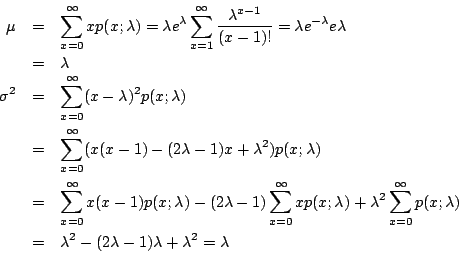
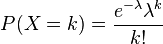
    No comments:

    Post a Comment

    Subscribe to: Post Comments (Atom)