为什么说物体在均匀引力场的运动规律等价于在匀加速参考系 ...
wenwen.sogou.com/z/q551727870.htm - 轉為繁體網頁
2014年5月7日 - 这是因为物体在均匀引力场的运动规律是相当于有一个不变的力在牵引着它而物体在匀加速参考系中的运动规律也是相当于有一个不变的力在牵引 ...引力时间膨胀可以在静态均匀引力场发生?_野薄荷
www.yebohe.cn/.../8669130312d8a8dbaf44f8c88283739f...
轉為繁體網頁
广义相对论预言的引力时间膨胀。计算扩张假定史瓦西度规在互联网上的公式(在不均匀的引力领域是)。所以问题是一个引力时间膨胀发生在静态均匀引力场?轉為繁體網頁
什么是引力场_好搜问答 - 奇虎
wenda.haosou.com/search?q=什么是引力场 - 轉為繁體網頁
... 场强是什么关系?均匀引力场是什么意思? 其实在非均匀引力场中,引力场和引力势的关系只能是定性分析,而不能定量 若是在均匀引力场中(均匀引力场是指&nbs.非稳定均匀引力场 9与时空r和t有关 广义坐标与局部惯性坐标 ...
blog.sina.com.cn/s/blog_a582cd40010174uz.html - 轉為繁體網頁
2012年7月16日 - 另一方面, 按照等价原理, 在匀加速坐标系. ' z = z 一9 一x = g, t 一t :. 中,惯性力可以抵消均匀恒定的引力9.而一般非稳定均匀引力场,9与时空r ...科学网—相对论对话录10 - 吴新忠的博文 - 科学网—博客
blog.sciencenet.cn/blog-1668877-898987.html
轉為繁體網頁
2015年6月18日 - 答:爱因斯坦在利用等效原理计算光线偏折时,把太阳表面附近的引力场近似视为均匀引力场处理,结果就得到了与牛顿力学中引力场引发的光线偏 ...轉為繁體網頁
[PDF]关于运动载体引力与惯性力的分离问题 - 中国科技论文在线
www.paper.edu.cn/scholar/.../shenwenbin449221-200903-... - 轉為繁體網頁
均匀引力场可用惯性力场来等效。另一. 方面,若考察在均匀引力场中自由降落的载体的. 内部,其重力梯度仪必然感受到零结果。一个简. 例是让载体静止,这时,在载体中 ...广义相对论的基本概念解释
old.hssyxx.com/zhsj/kexue-2/zutiweb/zu27/007/03.htm
轉為繁體網頁
它说明:如果一个惯性系相对于一个伽利略系被均匀地加速,那么我们就可以通过引入相对于它的一个均匀引力场而认为它(该惯性系)是静止的。 让我们来考查一个 ...轉為繁體網頁
球壳内部的均匀力场
作者:苏剑林 | 发布时间:October 16, 2010
也许不少同好已经在一些书籍上看到过这样的论述:
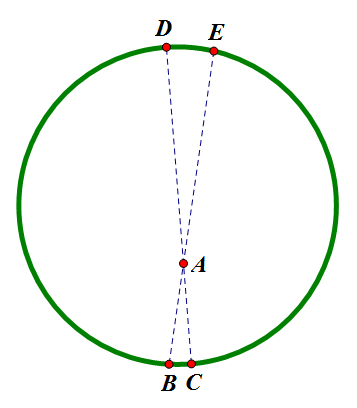
如图,我们要证明A点所受到的引力之和为0。过A点可以作两个立体角很小的对顶的圆锥,化成平面图就是图中“ΔABC和ΔADE”或“ΔAGF和ΔAHI”。以前者为例,当对顶角很小时,我们可以把DE和BC部分都其视为质点处理,并且将DE和BC看成直线(注意,它们本不是一条线,而是一个凸起的圆;看成直线后他们就是一个平面上的圆)。分别计算它们对A点的引力
FABC=GMBCMAAB2
FADE=GMDEMAAD2
由于密度均匀
MBCMDE=SBCSDE=AB2AD2代入后,我们发现
F_{ABC}=F_{ADE}$
也就是说,这两个部分的引力抵消了。一个球壳可以做无限次这种分割,而它们的引力都相互抵消,换句话说球壳的每个点对A的引力都会有另外一个点与之抵消,于是A点所受的引力为0。
由于静电力场具有和万有引力场类似的性质(和距离平方成反比),因而不难类比到,当球壳上均匀布满同种电荷时,球壳内任意点电荷所受的静电力合力为零。这时,我们不禁产生一个疑问:电荷有正负之分,要是球壳被平均分成两半,各自都均匀地分布着等量的异种电荷,那么内部的电场是怎样的呢?
也许有朋友猜测也是匀强的,不过这样想的朋友错了。请看下图
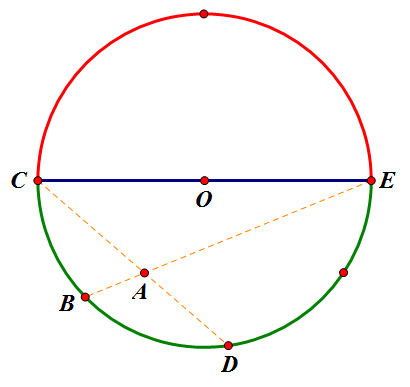
蓝色弧和红色弧分别代表带等量的异种电荷,分析点A的受力情况,根据上面的推导方法,由于BC与DE两段弧(实际是两个凸圆)的静电力相互抵消,红色弧与BD弧的静电力相等,而且方向相同,因此可以看成:A点的受力等于半球壳CE(红色弧)对A点的合力的两倍。要是受力均匀,那就是说半球壳CE对任意点的静电力相等,这显然不符合事实。
转载请包括本文地址:http://spaces.ac.cn/index.php/archives/988/
各向同性的薄球壳,其内部任意一点所受到来自球壳的引力为0。这是一个很神奇的事情,因为这意味着这是一个均匀引力场,虽然我们在很多问题上都假设了引力场均匀,但是我们却很难知道如何构造一个真正的均匀引力场(而构造一个真正的均匀力场都分析某些问题是很有用的,例如推导一些比例系数),现在眼前就摆着一个均匀引力场了。并且利用它我们就可以计算均匀实心球内部一点所受到的引力(等于它与一个球体的引力)。而关于它的证明,当然也可以利用微积分的知识,可是我们在这里介绍一个初等的方法,相信它会使我们更加感受到物理的神奇和有趣。

如图,我们要证明A点所受到的引力之和为0。过A点可以作两个立体角很小的对顶的圆锥,化成平面图就是图中“ΔABC和ΔADE”或“ΔAGF和ΔAHI”。以前者为例,当对顶角很小时,我们可以把DE和BC部分都其视为质点处理,并且将DE和BC看成直线(注意,它们本不是一条线,而是一个凸起的圆;看成直线后他们就是一个平面上的圆)。分别计算它们对A点的引力
由于密度均匀
也就是说,这两个部分的引力抵消了。一个球壳可以做无限次这种分割,而它们的引力都相互抵消,换句话说球壳的每个点对A的引力都会有另外一个点与之抵消,于是A点所受的引力为0。
由于静电力场具有和万有引力场类似的性质(和距离平方成反比),因而不难类比到,当球壳上均匀布满同种电荷时,球壳内任意点电荷所受的静电力合力为零。这时,我们不禁产生一个疑问:电荷有正负之分,要是球壳被平均分成两半,各自都均匀地分布着等量的异种电荷,那么内部的电场是怎样的呢?
也许有朋友猜测也是匀强的,不过这样想的朋友错了。请看下图

蓝色弧和红色弧分别代表带等量的异种电荷,分析点A的受力情况,根据上面的推导方法,由于BC与DE两段弧(实际是两个凸圆)的静电力相互抵消,红色弧与BD弧的静电力相等,而且方向相同,因此可以看成:A点的受力等于半球壳CE(红色弧)对A点的合力的两倍。要是受力均匀,那就是说半球壳CE对任意点的静电力相等,这显然不符合事实。
转载请包括本文地址:http://spaces.ac.cn/index.php/archives/988/
No comments:
Post a Comment