強力與引力都有非局域性(Non-Local)特征,這些是傳統的微擾方法無法解釋的,比如說強力中的色禁閉和漸近自由現象,引力的非局域性引出的問題就更多了。因此我們認為強力和引力場都是在二階上遞歸的力。引力有可加性,所以必須引入加法算符,但從邏輯上我們就知道這種引力理論一定是不可重正的,因為加法算符與遞歸算符是不相容的。但自然界中有很多二階細胞的實例,也就是多細胞生物。直觀的理解我們就知道量子細胞引力理論一定的超可重正的,註意這裏的超可重正性與量子場論中的超可重正性不是一個概念
Protein Structure - Medical Biochemistry
themedicalbiochemistrypage.org/protein-structure.php
Oct 16, 2015 - The primary structure of peptides and proteins refers to the linear number .... non-Forces influencing protein structure, Protein secondary ...
www.mikeblaber.org/oldwine/BCH4053/Lecture10/Lecture10.htm
Forces influencing protein structure, Primary and secondary structure ... Non-Protein structure - Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Protein_structure
Protein structure is the three-dimensional arrangement of atoms in a protein .... by the same non-covalent interactions and disulfide bonds as the tertiary structure. ... structure that is self-stabilizing and often folds independently of the rest of the ...
Wikipedia
Loading...
People also ask
Protein Structures: Primary, Secondary, Tertiary, Quaternary ...
schoolworkhelper.net › Science › Biology
Thus primary structure involves only the covalent bonds linking residues togetherexplain what forces are involved at each level of protein ...
https://answers.yahoo.com/question/index?qid...
Sep 20, 2011 - Therefore, tertiary structure also describes the relationship of ... by the same non-Tertiary Structure
www.austincc.edu/.../tertiary.htm
The tertiary structure of a protein is a description of the complex and irregular folding ... hydrophobic interactions between nonpolar R-groups; covalent bonds: The ... This bond is known as a disulfide bond and it acts as to stabilize the tertiary ...
Austin Community College District
Loading...
Protein Structure: Primary, Secondary, Tertiary, Quatemary ...
www.particlesciences.com/news/technical-briefs/.../protein-structure.html
It will also cover briefly how protein structure can be affected during ... many stabilizing forces due to bonding interactions between the side-chain groups of the ... non-polar amino acids such as phenylalanine or isoleucine tend to be buried on ...[PPT]CHAPTER 6
https://iweb.tntech.edu/tbanks/4610/GGch6web.ppt
What noncovalent interactions stabilize protein structure ? ... Secondary, tertiary, and quaternary structure of proteins are formed and stabilized by weak forces ...标签引力下的文章- 科学空间|Scientific Spaces
spaces.ac.cn/tag/引力/
轉為繁體網頁
阅读剩余部分. ... 之前已经稍微提及到了MTW的《引力论》,这本由C.W.麦思纳(轉為繁體網頁
相对论的历史与哲学 - 上海交通大学科学史与科学
shc2000.sjtu.edu.cn/0612/xiangduil.htm
轉為繁體網頁
相对论的建立来源于经典物理内部力学图景和电磁图景的冲突:在本体论上表现为粒子 .... 爱因斯坦一开始企图改造牛顿引力论并把它纳入狭义相对论的框架中。 .... 这是一种由于转动造成的宇宙物质对球体的万有引力失去原来的平衡达到的剩余引力轉為繁體網頁
引力的非局域性引出的問題就更多了。 - phymath999
phymath999.blogspot.com/2013/02/non-local.html
2013年2月2日 - 強力與引力都有非局域性(Non-Local)特征,這些是傳統的微擾方法無法 ...... 它們的縱向分量有一部分恰好是抵消的,剩余的部分就是庫侖力,只是自 ...phymath999: 核力不是强力,而是强力的剩余相互作用。“饱和 ...
phymath999.blogspot.com/2014/05/blog-post_27.html
轉為繁體網頁
2014年5月27日 - 核力不是强力,而是强力的剩余相互作用。“饱和性”是从原子、分子间相互作用力那里借过来的,表示核子只与邻近的数目有限的几个核子之间发生 ...轉為繁體網頁
phymath999: 核力是强相互作用的剩余作用力; 核力与电荷 ...
phymath999.blogspot.com/2014/09/blog-post_84.html
轉為繁體網頁
2014年9月18日 - 核力是强相互作用的剩余作用力; 核力与电荷无关。据此可以认为,原子核内的质子和中子其实是同一种粒子——“核子”在一种内禀的“同位旋空间”中 ...轉為繁體網頁
phymath999: ev01 原子核:核子束縛能:約MeV級。一般為 ...
phymath999.blogspot.com/2013/07/ev01-mev.html
2013年7月19日 - 核力:. 將質子與中子視為同類粒子。 一般為吸引力,比電磁力約大35倍。 為短程 ...... 質量,剩餘的3.978 MeV則由此二電子以動能形式攜帶。phymath999: solid-state ch6 計算總電荷數、總能,或其他 ...
phymath999.blogspot.hk/2014/05/solid-state-ch6-69.html
2014年5月3日 - phymath999 ... 完全不受離子位勢影響而得以自由活動,並且也沒有感受到電子與電子之間的庫倫力。 ..... 核力不是强力,而是强力的剩余相互作用。phymath999: 燦爛的星空(亮線):高溫、低密度氣體所發出的 ...
phymath999.blogspot.co.uk/2014/05/blog-post_8745.html
2014年5月30日 - phymath999 ..... 核力不是强力,而是强力的剩余相互作用。“饱和性”是从原子、分子间相互作用力那里借过来的,表示核子只与... 电子的“交换作用”是 ...廣義拉格耳多項式| 互联网上引用| cyclopaedia.net
zh.cyclopaedia.asia/wiki/廣義拉格耳多項式
phymath999: 因為電子與電子之間的庫侖相互作用,擁有多個電子的. ... 空间正规偏微分方程组正惯性指数正比例函数整系数多项式整数剩余类环... 广义施勒米希级数 ...
量子細胞場論是統一場論的關鍵 [引用 2009-6-26 20:20:54]
(轉帖此文純粹是出於興趣,但我根本看不懂。文章涉及相對論、量子力學、超弦理論、統一場構想等。
請有理工科背景的網友簡單、形象地介紹一下。
文章來源: 三思科學網 henryharry2 )
量子細胞場論是唯一與現有的粒子物理標準模型和廣義相對論兩者都最大兼容的(Maximal Compatible)模型。所謂最大兼容是指在可觀測效應上兩者完全兼容,在不可觀測效應上兩者略有差異。量子細胞場論的出發點有兩個:一是射影叢,二是細胞量子化。
由幾何的觀點我們知道,洛侖茲群(Lorentz Group)是一個酉模仿射群,因此我們應當從射影群出發定義協變性,由於還沒有人仔細研究這個群,我們不妨稱之為愛因斯坦群。所以要與狹義相對論相容,引入射影空間是必然的,我們稱之為愛因斯坦空間,這是一個完備的空間,是由酉模仿射空間加上它的射影補丁構成的。要與規範場論兼容,則引入射影叢也是必然的,也就是說,射影變換不是全局的,而是在空間中的每一點定義的。這裏沒有歐氏空間中的絕對原點,只有相對原點。
所謂細胞量子化,是推測粒子是一種自對偶的細胞。普通的細胞具有粒子性也具有不確定性,不確定性是由於食物分布的不確定性引起的,所以細胞既有粒子的特點也有場的特點,但這種場具有與背景相關的特點。因此我們說粒子是一種自對偶的細胞,想象粒子有一個與之伴隨的對偶細胞是在空間中隨機分布的,但這種分布只與粒子本身有關。這樣我們就擯棄了以太說,也不再需要Dirac海,不需要虛空間中充滿了檢測不到的希格斯粒子。規範場是相位因子場,而相位因子與量子細胞周期是等價的概念。
量子細胞場論的最大特點是一切推導過程都是自然的,規範場論通過引入規範變換增加了場的自由度,然後通過指定規範再限制自由度,但這種增加與限制自由度的方法都是人為引入的。量子細胞場論則不同,射影空間有最大的自由度,物理空間有最小的自由度,但眾所周知,洛侖茲群是非緊致(Non-compact)群,當我們要求物理空間必須是緊致的(Compact)。從Klein的變換群等級可以知道,射影群引出的聯絡必須約化成U(1)、SU(2)和SU(3)群,也就是標準模型中定義聯絡的幾個群。
另一方面,由Klein的變換群觀點可知,物理空間中愛因斯坦群必須約化成保持幺正性的旋轉群,這就很自然地引出了自旋。平移變換只能作為一種導出的結果,傳統方法也可以導出類似的結論;比如你可以從共形群(Conformal)出發導出自旋,也是一種先增加很多自由度,再限制自由度的方法,相比之下,會使問題復雜化。
由非對易幾何出發,可以導出中間矢量玻色子的質量是一種電弱“磁”效應,同樣由量子細胞場論出發,也可以導出類似的結果。平移變換只能是一種導出結果,由射影群到酉模仿射群,能夠保持相對原點不變的變換只可能有兩種,一種就是傳統意義上的“電荷”,另外一種就是“質心荷”,這是標準模型中沒有考慮的情況。射影空間中有點與線的對偶性,投射到物理空間,可以自然地引出玻色子的縱向極化分量。所以說,量子細胞場論是一種最簡單的同時滿足可重正化要求又能引入玻色子質量的模型。
量子引力理論一直困難重重。使用正則量子化方法的圈量子引力是一種背景無關的理論;超引力遭遇到不可重正性的難題;廣義相對論是背景無關的,弦論雖可解決重正化難題,卻是一種背景相關的理論,發展下去也必須引入以太、Dirac海和希格斯(Higgs)粒子等類似的概念,例如超弦允許有多達數萬種的真空狀態。引力子的自旋為2,要想將引力量子化,超對稱性是必需的,在超引力和弦論中,超對稱性又是人為引入的,就導出了沒有實驗依據的超夥伴粒子,並且這樣的理論也是醜陋的,很難想象造物主會用這麽醜陋的方式創造世界。細胞量子化方式卻是自然地引入了超對稱性。
遞歸
請有理工科背景的網友簡單、形象地介紹一下。
文章來源: 三思科學網 henryharry2 )
量子細胞場論是統一場論的關鍵
量子細胞場論是唯一與現有的粒子物理標準模型和廣義相對論兩者都最大兼容的(Maximal Compatible)模型。所謂最大兼容是指在可觀測效應上兩者完全兼容,在不可觀測效應上兩者略有差異。量子細胞場論的出發點有兩個:一是射影叢,二是細胞量子化。
由幾何的觀點我們知道,洛侖茲群(Lorentz Group)是一個酉模仿射群,因此我們應當從射影群出發定義協變性,由於還沒有人仔細研究這個群,我們不妨稱之為愛因斯坦群。所以要與狹義相對論相容,引入射影空間是必然的,我們稱之為愛因斯坦空間,這是一個完備的空間,是由酉模仿射空間加上它的射影補丁構成的。要與規範場論兼容,則引入射影叢也是必然的,也就是說,射影變換不是全局的,而是在空間中的每一點定義的。這裏沒有歐氏空間中的絕對原點,只有相對原點。
所謂細胞量子化,是推測粒子是一種自對偶的細胞。普通的細胞具有粒子性也具有不確定性,不確定性是由於食物分布的不確定性引起的,所以細胞既有粒子的特點也有場的特點,但這種場具有與背景相關的特點。因此我們說粒子是一種自對偶的細胞,想象粒子有一個與之伴隨的對偶細胞是在空間中隨機分布的,但這種分布只與粒子本身有關。這樣我們就擯棄了以太說,也不再需要Dirac海,不需要虛空間中充滿了檢測不到的希格斯粒子。規範場是相位因子場,而相位因子與量子細胞周期是等價的概念。
量子細胞場論的最大特點是一切推導過程都是自然的,規範場論通過引入規範變換增加了場的自由度,然後通過指定規範再限制自由度,但這種增加與限制自由度的方法都是人為引入的。量子細胞場論則不同,射影空間有最大的自由度,物理空間有最小的自由度,但眾所周知,洛侖茲群是非緊致(Non-compact)群,當我們要求物理空間必須是緊致的(Compact)。從Klein的變換群等級可以知道,射影群引出的聯絡必須約化成U(1)、SU(2)和SU(3)群,也就是標準模型中定義聯絡的幾個群。
另一方面,由Klein的變換群觀點可知,物理空間中愛因斯坦群必須約化成保持幺正性的旋轉群,這就很自然地引出了自旋。平移變換只能作為一種導出的結果,傳統方法也可以導出類似的結論;比如你可以從共形群(Conformal)出發導出自旋,也是一種先增加很多自由度,再限制自由度的方法,相比之下,會使問題復雜化。
由非對易幾何出發,可以導出中間矢量玻色子的質量是一種電弱“磁”效應,同樣由量子細胞場論出發,也可以導出類似的結果。平移變換只能是一種導出結果,由射影群到酉模仿射群,能夠保持相對原點不變的變換只可能有兩種,一種就是傳統意義上的“電荷”,另外一種就是“質心荷”,這是標準模型中沒有考慮的情況。射影空間中有點與線的對偶性,投射到物理空間,可以自然地引出玻色子的縱向極化分量。所以說,量子細胞場論是一種最簡單的同時滿足可重正化要求又能引入玻色子質量的模型。
量子引力理論一直困難重重。使用正則量子化方法的圈量子引力是一種背景無關的理論;超引力遭遇到不可重正性的難題;廣義相對論是背景無關的,弦論雖可解決重正化難題,卻是一種背景相關的理論,發展下去也必須引入以太、Dirac海和希格斯(Higgs)粒子等類似的概念,例如超弦允許有多達數萬種的真空狀態。引力子的自旋為2,要想將引力量子化,超對稱性是必需的,在超引力和弦論中,超對稱性又是人為引入的,就導出了沒有實驗依據的超夥伴粒子,並且這樣的理論也是醜陋的,很難想象造物主會用這麽醜陋的方式創造世界。細胞量子化方式卻是自然地引入了超對稱性。
遞歸
弦論無法解決粒子的手征性問題,只有引入超對稱性和高維空間後,超弦才能解決手征性問題。手征性在量子細胞場論裏不是問題,我們假定電子中微子是零階細胞,而電子為一階細胞就可以了,現實世界中零階細胞包括病毒等,一階細胞包含細菌等,這在形式邏輯中有一個對應物,就是一階謂詞邏輯,就是哥德爾(Godel)發現不完備定理的那個邏輯。
同一階謂詞邏輯不一樣的地方,這裏我們引入了一個一階遞歸(First-Order Recursive)算符,一階算符在很多量子場論裏都是必須的,比如非對易幾何,再比如Dirac場(可以參見Greiner寫的《量子力學導論》),但遞歸算符卻是可重正化理論要求的。
重正化與標度不變性有關,當我們實施一個標度變換,相應的場不會因為標度變換而發生改變,我們才說這個場論是可重正的。所以量子場論裏的信使粒子必須是無質量的,質量的存在會破壞標度不變性。量子細胞場論裏可以運用動態重正化技術,相信這種動態重正化技術對於強相互作用以及量子引力是必要的技術,為了有所區別我們將傳統量子場論中的重正化技術稱為靜態重正化技術。酉模仿射變換可以保持兩類相對原點不變,即電荷不變性與質心荷的不變性,當我們要求一階條件時,很自然粒子的電荷與質心荷必須重合,這就引出了Dirac場,由於Dirac場、Gordan場與傳統的Schodinger場都是色散場,動態重正化技術保證了電荷與質心荷在色散場中也保持重合。所以可以認為遞歸條件是量子細胞場論裏的Ward恒等式。
為了看清量子細胞場論與量子場論的關系,我們引入線性邏輯中的復制算符“!”和對偶“?”,我們知道它們等價於量子場論中的產生和湮滅算符。公理化量子場論的基礎是直覺邏輯,通過復制算符和對偶算符可以將直覺邏輯嵌入到線性邏輯中,從而量子細胞場論與量子場論是嚴格等價的;但有一個重要的區別,線性邏輯尊重資源有限的事實,這就給二次量子化加了一個限制,所以原則上量子細胞場論可以是一門拋棄了無窮大的學問;量子場論中虛粒子可以被任意的復制正是無窮大產生的根源。
自旋是量子場論中最基本的概念,可以說不了解自旋就不可能明白量子場論;但自旋沒有經典物理的對應物,想像如果電子像地球一樣自轉的話,電子的表面將不得不以光速的兩倍旋轉,這顯然是不可能的;量子場論中只能以較抽象的方式討論自旋,估計盯著Dirac方程看上半天也未必能明白自旋是怎麽回事。實際上,自旋在細胞的世界裏是有對應物的,就是細胞周期,還有就是人體內的能量ATP循環,ATP循環只是一種邏輯上的旋轉,只有當你說話或者走路的時候才會轉化成真實的物理波動。對於量子細胞而言,自旋、遞歸和量子細胞分裂是嚴格等價的,這是狹義相對論所要求的;狹義相對論是一種超等的理論,洛倫茲對稱性是嚴格成立的;但生物中的細胞分裂能夠實現的是一種偽遞歸,用普裏高津的話說,生物是一種耗散結構,對稱性被破壞了。
同一階謂詞邏輯不一樣的地方,這裏我們引入了一個一階遞歸(First-Order Recursive)算符,一階算符在很多量子場論裏都是必須的,比如非對易幾何,再比如Dirac場(可以參見Greiner寫的《量子力學導論》),但遞歸算符卻是可重正化理論要求的。
重正化與標度不變性有關,當我們實施一個標度變換,相應的場不會因為標度變換而發生改變,我們才說這個場論是可重正的。所以量子場論裏的信使粒子必須是無質量的,質量的存在會破壞標度不變性。量子細胞場論裏可以運用動態重正化技術,相信這種動態重正化技術對於強相互作用以及量子引力是必要的技術,為了有所區別我們將傳統量子場論中的重正化技術稱為靜態重正化技術。酉模仿射變換可以保持兩類相對原點不變,即電荷不變性與質心荷的不變性,當我們要求一階條件時,很自然粒子的電荷與質心荷必須重合,這就引出了Dirac場,由於Dirac場、Gordan場與傳統的Schodinger場都是色散場,動態重正化技術保證了電荷與質心荷在色散場中也保持重合。所以可以認為遞歸條件是量子細胞場論裏的Ward恒等式。
為了看清量子細胞場論與量子場論的關系,我們引入線性邏輯中的復制算符“!”和對偶“?”,我們知道它們等價於量子場論中的產生和湮滅算符。公理化量子場論的基礎是直覺邏輯,通過復制算符和對偶算符可以將直覺邏輯嵌入到線性邏輯中,從而量子細胞場論與量子場論是嚴格等價的;但有一個重要的區別,線性邏輯尊重資源有限的事實,這就給二次量子化加了一個限制,所以原則上量子細胞場論可以是一門拋棄了無窮大的學問;量子場論中虛粒子可以被任意的復制正是無窮大產生的根源。
自旋是量子場論中最基本的概念,可以說不了解自旋就不可能明白量子場論;但自旋沒有經典物理的對應物,想像如果電子像地球一樣自轉的話,電子的表面將不得不以光速的兩倍旋轉,這顯然是不可能的;量子場論中只能以較抽象的方式討論自旋,估計盯著Dirac方程看上半天也未必能明白自旋是怎麽回事。實際上,自旋在細胞的世界裏是有對應物的,就是細胞周期,還有就是人體內的能量ATP循環,ATP循環只是一種邏輯上的旋轉,只有當你說話或者走路的時候才會轉化成真實的物理波動。對於量子細胞而言,自旋、遞歸和量子細胞分裂是嚴格等價的,這是狹義相對論所要求的;狹義相對論是一種超等的理論,洛倫茲對稱性是嚴格成立的;但生物中的細胞分裂能夠實現的是一種偽遞歸,用普裏高津的話說,生物是一種耗散結構,對稱性被破壞了。
字典
細胞量子化是一種與路徑積分量子化方法大體上兼容的量子化方法,但細胞量子化更側重於數學上所謂的微局部分析,我們更關心一個自對偶細胞周期內發生的事情;由於有質量粒子與無質量粒子明顯存在於一個雙曲空間中,加上逆歸條件和動態重正化方法,自然可以得出費米子波函數的反對稱統計性質;細胞量子化方法還有一個好處是可以用統一的幾何語言處理對稱統計和重正化問題。對費米子場而言,對偶性與手征性是等價的。以光子為例,電場與磁場相互轉化,但光子的總能量是固定不變的;所以,量子細胞有零點能,一對相互對偶的場互相轉化,將場進行傅裏葉變換就得到對偶場,零點能就相當於自對偶的帕斯瓦爾定理。
由於荷與無窮遠直線有兩個交點,因此對應的是雙曲幾何,引出的力是排斥性的。玻色子滿足諧和坐標條件,相應的微分算子是橢圓的,與無窮遠直線沒有交點,引出的力是吸引性的。這可以解釋廣義相對論引出的宇宙學疑難,量子引力在產生吸引力的同時,也產生著斥力;所以宇宙快速膨脹的原因也是量子引力的一個效應,不必是大爆炸的產物。
我們的宇宙沒有起點,也沒有終點,而是一個超級宇宙中不斷波動著的一個超級基本粒子。這體現了馬克思主義宇宙觀的回歸,無數與我們的宇宙類似的超級基本粒子組成了超級宇宙,而這個超級宇宙確實是無邊無界的。
動態重正化技術自然地保證了費米子的自旋是1/2,動態重正化可以看成是自對偶細胞的細胞分裂過程,現在世界中,細菌通過細胞分裂自我繁殖。為了看清射影幾何與量子細胞場論之間的關系,我們需要射影叢幾何與量子場論對應關系的一個字典。
將復射影空間投射到仿射空間中,酉模仿射變換可以保持一個無窮遠直線不變,並且可以保持兩個虛園點不變,這樣我們就建立了與量子場論對應關系的一個字典。
將復射影空間投射到仿射空間中,酉模仿射變換可以保持一個無窮遠直線不變,並且可以保持兩個虛園點不變,這樣我們就建立了與量子場論對應關系的一個字典。
| 復射影空間中的概念 | 量子場論中的概念 |
| 虛園點(Circular Point) | 正電荷或負電荷 |
| 無窮遠直線 | 光子的世界線 |
| 酉模仿射變換 | 洛倫茲變換 |
| 仿射補丁 | 荷 |
| 點線對稱性 | 電流連續性方程 |
| 二級退化曲線 | 核力同位旋場,Higgs復標量場 |
| 二級退化曲線X+iY | 帶正電荷的W玻色子場 |
| 二級退化曲線X-iY | 帶負電荷的W玻色子場 |
| 水平正交標架 | 愛因斯坦-玻色統計 |
| 垂直正交標架 | 費米-狄拉克統計 |
細胞量子化是一種與路徑積分量子化方法大體上兼容的量子化方法,但細胞量子化更側重於數學上所謂的微局部分析,我們更關心一個自對偶細胞周期內發生的事情;由於有質量粒子與無質量粒子明顯存在於一個雙曲空間中,加上逆歸條件和動態重正化方法,自然可以得出費米子波函數的反對稱統計性質;細胞量子化方法還有一個好處是可以用統一的幾何語言處理對稱統計和重正化問題。對費米子場而言,對偶性與手征性是等價的。以光子為例,電場與磁場相互轉化,但光子的總能量是固定不變的;所以,量子細胞有零點能,一對相互對偶的場互相轉化,將場進行傅裏葉變換就得到對偶場,零點能就相當於自對偶的帕斯瓦爾定理。
由於荷與無窮遠直線有兩個交點,因此對應的是雙曲幾何,引出的力是排斥性的。玻色子滿足諧和坐標條件,相應的微分算子是橢圓的,與無窮遠直線沒有交點,引出的力是吸引性的。這可以解釋廣義相對論引出的宇宙學疑難,量子引力在產生吸引力的同時,也產生著斥力;所以宇宙快速膨脹的原因也是量子引力的一個效應,不必是大爆炸的產物。
我們的宇宙沒有起點,也沒有終點,而是一個超級宇宙中不斷波動著的一個超級基本粒子。這體現了馬克思主義宇宙觀的回歸,無數與我們的宇宙類似的超級基本粒子組成了超級宇宙,而這個超級宇宙確實是無邊無界的。
二次量子化
量子細胞場論使我們隱約看到了另外一種對稱性,回答諸如為什麽核力與電弱理論的不變群都是SU(2),為什麽味對稱群和量子色動力學規範群都是SU(3)等問題。
強力與引力都有非局域性(Non-Local)特征,這些是傳統的微擾方法無法解釋的,比如說強力中的色禁閉和漸近自由現象,引力的非局域性引出的問題就更多了。因此我們認為強力和引力場都是在二階上遞歸的力。引力有可加性,所以必須引入加法算符,但從邏輯上我們就知道這種引力理論一定是不可重正的,因為加法算符與遞歸算符是不相容的。但自然界中有很多二階細胞的實例,也就是多細胞生物。直觀的理解我們就知道量子細胞引力理論一定的超可重正的,註意這裏的超可重正性與量子場論中的超可重正性不是一個概念。
這是因為多細胞生物有著全息效應,即每一個細胞中都含有全部的遺傳信息,隨便選取一個細胞就可以克隆出一個完整的生物體。回想馬德西納(Maldcena)關於量子引力與規範理論對偶性關系的那篇著名文章基於的前提也是全息原理,大自然是多麽了解人的心思,現在越來越多的細節都走到一起來了。
酉模仿射群空間是不完備的,需要添加射影補丁,也就是無窮遠點後才是完備的。當我們退回射影空間,想進行二次量子化時,發現一個完備的空間必然是同時具有雙曲幾何與橢圓幾何性質的空間;用向量叢的語言來說,就是垂直空間滿足反對稱關系,水平空間滿足對稱關系,水平空間正確地復制出了愛因斯坦引力論;量子場論中對應的關系是費米子滿足反對稱統計,玻色子滿足對稱關系。
這種具有雙重特點的空間蘊含了由於對偶關系引出的超對稱性,雙曲變換群與橢圓變換群都是保持二次的絕對形不變的群,引力的這種奇特效應是射影空間中線-線對偶關系引出的;翻譯成物理的語言就是說,兩個實物粒子通過交換引力子產生引力,對偶地,兩個引力子也可以通過交換實物粒子產生斥力。
射影空間中的無窮遠點與普通的點並沒有本質的區別;投射回物理空間,荷也就是無窮遠點卻有可能是一個奇點,這也從另外一方面說明規範粒子一定是無質量的,只有無質量的粒子才能到達無窮遠的邊界點;空間的雙曲幾何性質也是量子場論中無窮大產生的根源,沿著一條無窮長的線積分肯定會產生奇異性,不過這種奇異性與黑洞的視界一樣不是本性奇點,可以通過一個適當的變換消除,所以我們推薦用動態重正化方法代替量子場論中的靜態重正化方法,象弦論一樣徹底消除積分的發散性。
無窮大是量子場論的一個包袱,量子場論是不自洽的,我們這種幾何上的事後諸葛亮式的論證提示了無窮大的起源,將無窮大變換成射影空間中的無窮遠點,從而量子細胞場論在邏輯上是自洽的。另一方面,由於有了無窮遠點,量子細胞場論和馬德西納理論站到了同一條起跑線上,但馬德西納理論卻需要另外的5個維度,另外對偶性是量子細胞場論的基本原理,應該能導出很多有趣的結論。
強力與引力都有非局域性(Non-Local)特征,這些是傳統的微擾方法無法解釋的,比如說強力中的色禁閉和漸近自由現象,引力的非局域性引出的問題就更多了。因此我們認為強力和引力場都是在二階上遞歸的力。引力有可加性,所以必須引入加法算符,但從邏輯上我們就知道這種引力理論一定是不可重正的,因為加法算符與遞歸算符是不相容的。但自然界中有很多二階細胞的實例,也就是多細胞生物。直觀的理解我們就知道量子細胞引力理論一定的超可重正的,註意這裏的超可重正性與量子場論中的超可重正性不是一個概念。
這是因為多細胞生物有著全息效應,即每一個細胞中都含有全部的遺傳信息,隨便選取一個細胞就可以克隆出一個完整的生物體。回想馬德西納(Maldcena)關於量子引力與規範理論對偶性關系的那篇著名文章基於的前提也是全息原理,大自然是多麽了解人的心思,現在越來越多的細節都走到一起來了。
酉模仿射群空間是不完備的,需要添加射影補丁,也就是無窮遠點後才是完備的。當我們退回射影空間,想進行二次量子化時,發現一個完備的空間必然是同時具有雙曲幾何與橢圓幾何性質的空間;用向量叢的語言來說,就是垂直空間滿足反對稱關系,水平空間滿足對稱關系,水平空間正確地復制出了愛因斯坦引力論;量子場論中對應的關系是費米子滿足反對稱統計,玻色子滿足對稱關系。
這種具有雙重特點的空間蘊含了由於對偶關系引出的超對稱性,雙曲變換群與橢圓變換群都是保持二次的絕對形不變的群,引力的這種奇特效應是射影空間中線-線對偶關系引出的;翻譯成物理的語言就是說,兩個實物粒子通過交換引力子產生引力,對偶地,兩個引力子也可以通過交換實物粒子產生斥力。
射影空間中的無窮遠點與普通的點並沒有本質的區別;投射回物理空間,荷也就是無窮遠點卻有可能是一個奇點,這也從另外一方面說明規範粒子一定是無質量的,只有無質量的粒子才能到達無窮遠的邊界點;空間的雙曲幾何性質也是量子場論中無窮大產生的根源,沿著一條無窮長的線積分肯定會產生奇異性,不過這種奇異性與黑洞的視界一樣不是本性奇點,可以通過一個適當的變換消除,所以我們推薦用動態重正化方法代替量子場論中的靜態重正化方法,象弦論一樣徹底消除積分的發散性。
無窮大是量子場論的一個包袱,量子場論是不自洽的,我們這種幾何上的事後諸葛亮式的論證提示了無窮大的起源,將無窮大變換成射影空間中的無窮遠點,從而量子細胞場論在邏輯上是自洽的。另一方面,由於有了無窮遠點,量子細胞場論和馬德西納理論站到了同一條起跑線上,但馬德西納理論卻需要另外的5個維度,另外對偶性是量子細胞場論的基本原理,應該能導出很多有趣的結論。
簡單的就是最好的
量子細胞場論大大簡化了傳統量子場論用到的數學。與冪零(Nil-potent)Dirac場方程用到的數學差不多,遞歸條件已經蘊含了費米子場是冪零的。
加進了二階加法算符後,計算機邏輯中有一個對應的邏輯,即並行邏輯。由並行重寫系統邏輯可知,當真空是反屏蔽時,自然可以通過重正化群導出不動點。但量子細胞場論與量子色動力學有一個差別:量子色動力學中是由重正化群導出不動點;而量子細胞場論中不動點是事先存在的,重正化群可以由不動點生成;也就是說,禁閉相、漸近自由和不動點在量子細胞場論完全是同一個原因引起的。冪零Dirac方程指出,強力可以不是由有色力傳導的,要想了解詳情可以參考有關冪零Dirac方程的原著(arxiv.org/abs/quant-ph/0301071)。因此,量子細胞場論完全可以解決強相互作用中所有的疑難。
引力引出的疑難有三個方面,宏觀的、微觀的和黑洞的。前面我們已經說過,傳統的重正化方法在量子引力中是決不會奏效的,那麽重正化群又如何。如果將強力比喻為量子世界中的植物的話;引力則像是量子世界中的動物,它們不會呆在一個地方不動,所以試圖用不動點理論解決引力的問題也是不可能奏效的,只有超可重正性能夠挽救引力。
超弦(Super-String)理論是為解釋強力誕生的,由於量子色動力學的成功,超弦發展為試圖解釋引力。量子細胞場論在解釋引力方面與弦論是有聯系的,遞歸條件引入了一種回歸效應,對應著開弦。由於沒有了不動點,我們只能退回到射影空間找不變性,我們能夠找到的是那些保持絕對形不變的射影群,即愛因斯坦群。愛因斯坦群在物理空間中的對應物不是別的,正是彎曲的時空,我們看到量子細胞場論與廣義相對論的兼容性是多麽好。那麽絕對形在微觀世界的對應物又是什麽,不是別的,正是我們在超弦理論中熟悉的閉弦。
我們看到了弦理論的回歸,不過量子細胞場論沒有手征性問題、沒有超對稱的問題,因此沒有必要像超弦理論一樣需要引力額外的時空維度再讓它們卷縮起來。量子細胞場論回歸的正是當年那個樸素的弦理論。量子細胞場論一方面繼承了量子場論中點粒子的看法,另一方面由於量子細胞的自對偶性,可以在空間中延展開,這同弦論的看法是一致的。
加進了二階加法算符後,計算機邏輯中有一個對應的邏輯,即並行邏輯。由並行重寫系統邏輯可知,當真空是反屏蔽時,自然可以通過重正化群導出不動點。但量子細胞場論與量子色動力學有一個差別:量子色動力學中是由重正化群導出不動點;而量子細胞場論中不動點是事先存在的,重正化群可以由不動點生成;也就是說,禁閉相、漸近自由和不動點在量子細胞場論完全是同一個原因引起的。冪零Dirac方程指出,強力可以不是由有色力傳導的,要想了解詳情可以參考有關冪零Dirac方程的原著(arxiv.org/abs/quant-ph/0301071)。因此,量子細胞場論完全可以解決強相互作用中所有的疑難。
引力引出的疑難有三個方面,宏觀的、微觀的和黑洞的。前面我們已經說過,傳統的重正化方法在量子引力中是決不會奏效的,那麽重正化群又如何。如果將強力比喻為量子世界中的植物的話;引力則像是量子世界中的動物,它們不會呆在一個地方不動,所以試圖用不動點理論解決引力的問題也是不可能奏效的,只有超可重正性能夠挽救引力。
超弦(Super-String)理論是為解釋強力誕生的,由於量子色動力學的成功,超弦發展為試圖解釋引力。量子細胞場論在解釋引力方面與弦論是有聯系的,遞歸條件引入了一種回歸效應,對應著開弦。由於沒有了不動點,我們只能退回到射影空間找不變性,我們能夠找到的是那些保持絕對形不變的射影群,即愛因斯坦群。愛因斯坦群在物理空間中的對應物不是別的,正是彎曲的時空,我們看到量子細胞場論與廣義相對論的兼容性是多麽好。那麽絕對形在微觀世界的對應物又是什麽,不是別的,正是我們在超弦理論中熟悉的閉弦。
我們看到了弦理論的回歸,不過量子細胞場論沒有手征性問題、沒有超對稱的問題,因此沒有必要像超弦理論一樣需要引力額外的時空維度再讓它們卷縮起來。量子細胞場論回歸的正是當年那個樸素的弦理論。量子細胞場論一方面繼承了量子場論中點粒子的看法,另一方面由於量子細胞的自對偶性,可以在空間中延展開,這同弦論的看法是一致的。
幾何學上的推演
坐標叢的截面是一種反對稱的微分形式,滿足Grassmann代數規則,其實有一種我們非常熟悉的Grassmann代數的特例,就是滿足費米-狄拉克統計的費米子。可以引出的一個結論就是,由很多費米子組成的超費米子滿足超泡利不相容原理。這是從廣義相對論無法推導出來的,因為廣義相對論只考慮了曲率沒有考慮饒率,質量是曲率的源,而自旋是饒率的源。
這可以消除奇點疑難,黑洞不會永遠塌縮下去而變為奇點,奇點是由廣義相對論推導出來的一個幻像。一方面從質量方面來看,很多費米子組成的超級實物粒子滿足超泡利不相容原理會阻止黑洞塌縮;另一方面,從能量方面來看,隨著黑洞內能量的升高,會有越來越多的費米子組成共振態的復合粒子,這些復合粒子是非常短命的,馬上就會通過強相互作用或電弱相互作用衰變而釋放出能量,這種作用產生的排斥力甚至超過第一種作用。為了方便起見,我們將第一種稱為質量不相容原理,第二種稱為能量不相容原理。
在廣義相對論中,質量和能量是等價的,而在量子力學中,質量和能量起到的作用是不等價的。這也提供了解決黑洞疑難的一個可能答案,就是黑洞的質量可能有一個上限,質量不相容原理能夠阻止黑洞塌縮,使黑洞維持在一個動態平衡的狀態;而當黑洞的能量超過一個上限以後,能量不相容原理開始起主導作用,當排斥超過吸引後,會引起黑洞爆炸。我們猜想遍布於宇宙中的Gamma爆可能就是黑洞爆炸引起的。
回顧一下我們的推導過程,我們嘗試用量子場論的秘密武器重正化和重正化群去解決量子引力問題,卻發現有一條行不通定理在等著我們,我們只好退回到射影空間尋找答案。當將射影幾何推廣到射影叢時,由於引力具有可加性,Klein幾何自然會推演到Cartan幾何,相應的引力理論稱為愛因斯坦-Cartan理論,相應的聯絡稱為自旋聯絡,微分算符稱為Dirac算子。
我們看到,非對易幾何與弦論的思想都有可取的部分,當我們嘗試將自旋聯絡量子化時,我們發現,那不是別的,正是閉弦;非對易幾何與弦論竟然分別是量子細胞引力理論的低能和高能極限。非對易幾何是一種背景無關的理論,弦論是一種背景相關的理論,量子細胞引力理論正是這兩種理論中間缺失的那道橋梁。量子細胞引力理論就這樣自然地將非對易幾何與弦論正確的部分統一了起來,由於這一系列推導過程都是自然的演進,所有的過程都是強制性的,我們根本沒有其它可選項;由此可知,量子細胞引力理論一定是正確的。
我們看到,非對易幾何與弦論的思想都有可取的部分,當我們嘗試將自旋聯絡量子化時,我們發現,那不是別的,正是閉弦;非對易幾何與弦論竟然分別是量子細胞引力理論的低能和高能極限。非對易幾何是一種背景無關的理論,弦論是一種背景相關的理論,量子細胞引力理論正是這兩種理論中間缺失的那道橋梁。量子細胞引力理論就這樣自然地將非對易幾何與弦論正確的部分統一了起來,由於這一系列推導過程都是自然的演進,所有的過程都是強制性的,我們根本沒有其它可選項;由此可知,量子細胞引力理論一定是正確的。
| 量子場論中的概念 | 量子引力中的概念 |
| 電荷 | 引力荷 |
| Gamma代數 | Grassmann代數 |
| 費米子 | 超費米子(雙曲幾何的邊界) |
| 泡利不相容原理 | 超泡利不相容原理 |
坐標叢的截面是一種反對稱的微分形式,滿足Grassmann代數規則,其實有一種我們非常熟悉的Grassmann代數的特例,就是滿足費米-狄拉克統計的費米子。可以引出的一個結論就是,由很多費米子組成的超費米子滿足超泡利不相容原理。這是從廣義相對論無法推導出來的,因為廣義相對論只考慮了曲率沒有考慮饒率,質量是曲率的源,而自旋是饒率的源。
這可以消除奇點疑難,黑洞不會永遠塌縮下去而變為奇點,奇點是由廣義相對論推導出來的一個幻像。一方面從質量方面來看,很多費米子組成的超級實物粒子滿足超泡利不相容原理會阻止黑洞塌縮;另一方面,從能量方面來看,隨著黑洞內能量的升高,會有越來越多的費米子組成共振態的復合粒子,這些復合粒子是非常短命的,馬上就會通過強相互作用或電弱相互作用衰變而釋放出能量,這種作用產生的排斥力甚至超過第一種作用。為了方便起見,我們將第一種稱為質量不相容原理,第二種稱為能量不相容原理。
在廣義相對論中,質量和能量是等價的,而在量子力學中,質量和能量起到的作用是不等價的。這也提供了解決黑洞疑難的一個可能答案,就是黑洞的質量可能有一個上限,質量不相容原理能夠阻止黑洞塌縮,使黑洞維持在一個動態平衡的狀態;而當黑洞的能量超過一個上限以後,能量不相容原理開始起主導作用,當排斥超過吸引後,會引起黑洞爆炸。我們猜想遍布於宇宙中的Gamma爆可能就是黑洞爆炸引起的。
一個最簡單的統一場論
量子細胞場論對費米子看法的改變不大,Dirac場位於一個二點離散空間與緊致空間的張量積空間中,構成了一個二葉(Two-sheet)不連通空間,電子就這樣瘋狂地在二個不連通空間中以27M每秒的速度跳來跳去,在量子細胞場論中電子就沒有這麽瘋狂了。
對玻色子的看法改變就很大了。以電磁力為例,光子只有自旋為1或-1的狀態,沒有自旋為零的狀態,但實際上,庫侖力主要是由這個自旋為0的標量光子傳導的,所以需要添加鬼粒子抵消該項多余的貢獻才能恢復幺正性。在射影幾何中有點線對偶性,自然可以得到一個自旋為0的標量粒子,但現在電磁力變成了一種內蘊的性質,考慮到黎曼幾何是一種內蘊的幾何,這就為我們建立統一場論奠定了基礎。
愛因斯坦的相對論實際上還是一種絕對時空觀,因為閔可夫斯基空間是一種偽歐氏空間,所以廣義相對論也會產生牛頓引力論相似的悖論,實際上牛頓引力論也可以看成是彎曲時空的引力論,只要做一個坐標變換就可以了;引力子也是引力場的源,這種自吞性的集合在邏輯學上是被禁止的,哥德爾不完備定理可以體現這一點。所以廣義相對論會產生很多悖論,比如空無一物的反de-Sitter空間會膨脹和時空奇點等。
量子細胞場論認為只有相互作用時時空才會彎曲,考慮時空中兩個粒子交換一對標量引力子。對電磁力來講,正電荷與負電荷是一對對合的點,我們自然也要求對標量引力論而言,兩個粒子的位置也必須是對合的;這是量子力學所要求的,希爾伯特空間是一個平方可積空間,幺正性要求可觀測量必需是自伴(self-adjoint)算子。這樣我們就建立了一個能夠正確產生出牛頓引力論的標量量子引力論,同時這個引力論也是與狹義相對論兼容的。
站在今天的立場你可能會反駁說,自旋為0同時質量為零的標量粒子從來都沒有觀測到。但時光倒回一個輪回(60年),也就是中華人民共和國成立那年,假如愛因斯坦堅持時空的相對性,同時不是堅信“上帝不擲骰子!”他老人家很可能會發現這個簡單的邏輯上自洽的統一場論,要知道那時人們還不知道弱力和強力。並且簡單統一場論是純幾何的,愛因斯坦一定喜歡。力產生的原因是純量子力學的,類似於兩個原子通過交換電子從而構成化學健。我們將自旋為0的引力子稱為牛頓引力子。
廣義相對論中,實物粒子與引力子服從同樣的方程,從現代量子場論的觀點來看顯然是病態的。量子電動力學中,電子與光子服從不同的方程,光子以最小耦合方式耦合進電磁場。簡單統一場論中實物粒子與引力子服從不同的方程,引力子以最小耦合方式耦合進引力場,引力子的方程在復數空間中滿足諧和坐標條件,我們知道這相當於電磁場的達朗貝爾方程。在射影空間中,點與線是對稱的,這在電磁場理論中相當於電荷與電流密度的對稱性,可以引出電流連續性方程;因此,簡單統一場論中,引力荷與引力流密度也是對稱的,可以引出引力流連續性方程,牛頓引力論和廣義相對論都忽略了這種對稱性。
對玻色子的看法改變就很大了。以電磁力為例,光子只有自旋為1或-1的狀態,沒有自旋為零的狀態,但實際上,庫侖力主要是由這個自旋為0的標量光子傳導的,所以需要添加鬼粒子抵消該項多余的貢獻才能恢復幺正性。在射影幾何中有點線對偶性,自然可以得到一個自旋為0的標量粒子,但現在電磁力變成了一種內蘊的性質,考慮到黎曼幾何是一種內蘊的幾何,這就為我們建立統一場論奠定了基礎。
愛因斯坦的相對論實際上還是一種絕對時空觀,因為閔可夫斯基空間是一種偽歐氏空間,所以廣義相對論也會產生牛頓引力論相似的悖論,實際上牛頓引力論也可以看成是彎曲時空的引力論,只要做一個坐標變換就可以了;引力子也是引力場的源,這種自吞性的集合在邏輯學上是被禁止的,哥德爾不完備定理可以體現這一點。所以廣義相對論會產生很多悖論,比如空無一物的反de-Sitter空間會膨脹和時空奇點等。
量子細胞場論認為只有相互作用時時空才會彎曲,考慮時空中兩個粒子交換一對標量引力子。對電磁力來講,正電荷與負電荷是一對對合的點,我們自然也要求對標量引力論而言,兩個粒子的位置也必須是對合的;這是量子力學所要求的,希爾伯特空間是一個平方可積空間,幺正性要求可觀測量必需是自伴(self-adjoint)算子。這樣我們就建立了一個能夠正確產生出牛頓引力論的標量量子引力論,同時這個引力論也是與狹義相對論兼容的。
站在今天的立場你可能會反駁說,自旋為0同時質量為零的標量粒子從來都沒有觀測到。但時光倒回一個輪回(60年),也就是中華人民共和國成立那年,假如愛因斯坦堅持時空的相對性,同時不是堅信“上帝不擲骰子!”他老人家很可能會發現這個簡單的邏輯上自洽的統一場論,要知道那時人們還不知道弱力和強力。並且簡單統一場論是純幾何的,愛因斯坦一定喜歡。力產生的原因是純量子力學的,類似於兩個原子通過交換電子從而構成化學健。我們將自旋為0的引力子稱為牛頓引力子。
廣義相對論中,實物粒子與引力子服從同樣的方程,從現代量子場論的觀點來看顯然是病態的。量子電動力學中,電子與光子服從不同的方程,光子以最小耦合方式耦合進電磁場。簡單統一場論中實物粒子與引力子服從不同的方程,引力子以最小耦合方式耦合進引力場,引力子的方程在復數空間中滿足諧和坐標條件,我們知道這相當於電磁場的達朗貝爾方程。在射影空間中,點與線是對稱的,這在電磁場理論中相當於電荷與電流密度的對稱性,可以引出電流連續性方程;因此,簡單統一場論中,引力荷與引力流密度也是對稱的,可以引出引力流連續性方程,牛頓引力論和廣義相對論都忽略了這種對稱性。
完整的統一場論
簡單統一場論與現代的觀點有很多不謀而合之處,這難道僅僅是巧合嗎? 簡單統一場論是規範不變的,規範不變性是由點線對偶性導出的。時空是五維的,用以構造射影空間中的齊次坐標,不過這多出的一維純粹是為了計算引入的,並不對應真實的物理維度;就像是量子場論中引入的鬼粒子,它們的存在只是為了恢復幺正性,並不對應真實的粒子。同時通過射影空間的對偶性我們發現了一條重要的關系:力=對偶性。量子場論中只有一種對稱性,即洛倫茲對稱性,而對偶性可以有很多;比如蜜蜂和花之間沒有對稱性而存在對偶性,蜜蜂有著朝花飛去的傾向,我們說蜜蜂和花之間存在吸引力。不過量子細胞顯然沒有生物細胞那麽復雜,量子細胞只需要攜帶能夠產生四種基本力的遺傳信息就足夠了。
這與那個神秘的M理論的中心觀點不謀而合,傳統量子場論從對稱性出發,認為力的根源在於對稱性,從後現代觀點來分析這是有問題的,對稱性引出自旋為1的光子,而實際上自旋為1的光子並不是庫侖力產生的真正原因,庫侖力的真正起因是標量光子。現代量子場並不排除自旋為0的無質量引力子的存在,例如通過真空自發破缺可以產生自旋為0的無質量粒子,只是這些無質量粒子都被中間規範玻色子吃掉了。
標量量子引力理論還需要擴展,原因是引力子還會與光子耦合,自旋為0的粒子不會與光子耦合,所以引力子的自旋必須是2。直接對廣義相對論中的度規量子化是不行的,原因是廣義相對論中的度規是非線性的,對聯絡量子化是可行的,沿著一個封閉的圓圈對聯絡積分可以導出一個不變曲率,實際上圈量子引力正是基於這種思想發展出來的,Yang-Mills場也可以通過這種方式量子化從而導出瞬子解。但圈量子引力面臨著一個尷尬,必須從聯絡導出度規,而圈量子引力理論做不到這一點,引力雖然量子化了,卻無法證明這個量子引力論與廣義相對論的兼容性。量子細胞場論沒有這個問題,原因還是在於對偶性,類似於簡單統一場論中的方法,實際光子的狀態是自旋為1的光子和標量光子的混合狀態。
自始至終我們都是沿著一條唯美的思想導出了統一場論的所有規則,怎一個美字了得,難道這一切不是必然的嗎? 現在可以肯定的是粒子就是自對偶的量子細胞,量子細胞帶有極性,極性是力的根源,極性滿足很好的代數規則,對費米子而言滿足費米-狄拉克統計,對玻色子而言滿足愛因斯坦-玻色統計。還有就是極性可以滿足布爾代數中的吸收律: A+A=A和消去律AA=A;比如你是一位由1萬億只細胞組成的小姐,雖然每只細胞都帶有小姐的遺傳信息,但只要一個量子數就可以表征了;量子力學中也有這樣一個例子,費曼的路徑積分法認為粒子經由所有可能的路徑由一點到達另外一點,但這些所有可能路徑的貢獻加在一起仍然是只要由一個量子數表征就足夠了。
量子場論的先輩們顯然忽略了吸收律,先輩們小心翼翼地摸著石頭過河,可能根本沒時間停下來欣賞大自然的美麗;我們卻可以踏著先輩們的足跡幸運地發現隱藏在大自然背後美麗的數學定律。吸收律在量子場論中就有直接的應用,以特Hooft的大N展開為例,假如色荷滿足吸收律,那麽N種顏色的量子色動力學就與3種顏色的量子色動力學是等價的,但N種顏色的量子色動力學的耦合常數可以很小,適合在微擾論的框架下進行計算。另一方面,如果費米-狄拉克統計和愛因斯坦-玻色統計關系成立的話,吸收律就意謂著超費米-狄拉克統計和超愛因斯坦-玻色統計也是成立的。
從吸收律出發也可以推斷出引力場也是一種自對偶的場,我們都很熟悉一種自對偶的場,就是電磁場,因此可以以量子電動力學為模板稍加改造發展出帶“權重”的引力場的量子理論。回想弱相互作用理論和強相互作用都是以量子電動力學為模板發展起來的,難免有一種英雄所見略同的感覺。
這與那個神秘的M理論的中心觀點不謀而合,傳統量子場論從對稱性出發,認為力的根源在於對稱性,從後現代觀點來分析這是有問題的,對稱性引出自旋為1的光子,而實際上自旋為1的光子並不是庫侖力產生的真正原因,庫侖力的真正起因是標量光子。現代量子場並不排除自旋為0的無質量引力子的存在,例如通過真空自發破缺可以產生自旋為0的無質量粒子,只是這些無質量粒子都被中間規範玻色子吃掉了。
標量量子引力理論還需要擴展,原因是引力子還會與光子耦合,自旋為0的粒子不會與光子耦合,所以引力子的自旋必須是2。直接對廣義相對論中的度規量子化是不行的,原因是廣義相對論中的度規是非線性的,對聯絡量子化是可行的,沿著一個封閉的圓圈對聯絡積分可以導出一個不變曲率,實際上圈量子引力正是基於這種思想發展出來的,Yang-Mills場也可以通過這種方式量子化從而導出瞬子解。但圈量子引力面臨著一個尷尬,必須從聯絡導出度規,而圈量子引力理論做不到這一點,引力雖然量子化了,卻無法證明這個量子引力論與廣義相對論的兼容性。量子細胞場論沒有這個問題,原因還是在於對偶性,類似於簡單統一場論中的方法,實際光子的狀態是自旋為1的光子和標量光子的混合狀態。
自始至終我們都是沿著一條唯美的思想導出了統一場論的所有規則,怎一個美字了得,難道這一切不是必然的嗎? 現在可以肯定的是粒子就是自對偶的量子細胞,量子細胞帶有極性,極性是力的根源,極性滿足很好的代數規則,對費米子而言滿足費米-狄拉克統計,對玻色子而言滿足愛因斯坦-玻色統計。還有就是極性可以滿足布爾代數中的吸收律: A+A=A和消去律AA=A;比如你是一位由1萬億只細胞組成的小姐,雖然每只細胞都帶有小姐的遺傳信息,但只要一個量子數就可以表征了;量子力學中也有這樣一個例子,費曼的路徑積分法認為粒子經由所有可能的路徑由一點到達另外一點,但這些所有可能路徑的貢獻加在一起仍然是只要由一個量子數表征就足夠了。
量子場論的先輩們顯然忽略了吸收律,先輩們小心翼翼地摸著石頭過河,可能根本沒時間停下來欣賞大自然的美麗;我們卻可以踏著先輩們的足跡幸運地發現隱藏在大自然背後美麗的數學定律。吸收律在量子場論中就有直接的應用,以特Hooft的大N展開為例,假如色荷滿足吸收律,那麽N種顏色的量子色動力學就與3種顏色的量子色動力學是等價的,但N種顏色的量子色動力學的耦合常數可以很小,適合在微擾論的框架下進行計算。另一方面,如果費米-狄拉克統計和愛因斯坦-玻色統計關系成立的話,吸收律就意謂著超費米-狄拉克統計和超愛因斯坦-玻色統計也是成立的。
從吸收律出發也可以推斷出引力場也是一種自對偶的場,我們都很熟悉一種自對偶的場,就是電磁場,因此可以以量子電動力學為模板稍加改造發展出帶“權重”的引力場的量子理論。回想弱相互作用理論和強相互作用都是以量子電動力學為模板發展起來的,難免有一種英雄所見略同的感覺。
較為深刻的結果
簡單統一場論通過最小耦合方式將質量與質量荷的作用分離開,可以推導出一些較為深刻的結果。首先,同牛頓和愛因斯坦引力論不同,引力耦合常數變為無量綱的,我們知道費米弱相互作用理論是不可重正化的,原因在於費米耦合常數與牛頓引力耦合常數有相同的量綱,所以需要引入Yang-Mills規範場和中間矢量玻色子使得弱耦合常數無量綱。
我們還是從Weyl引入規範場最初的原理出發,證明簡單統一場論確實是自洽的。考慮平面叢,由平面到平面的變換是10參數的群,當底流形為洛倫茲流形時,這個變換群與洛倫茲群是同構的。平面與平面之間可以定義聯絡和曲率式,當底流形為洛倫茲流形時,我們知道這正是電磁場的聯絡,詳細的證明可以參見陳省身老先生的演講。
簡單統一場論滿足可重正化最重要的條件,當實施一個標度變換後,與電荷一樣,引力荷沒有發生變化,感覺簡單統一場論應當是可以重正化的,但這需要一個嚴格的證明。
這裏,重正化的意思是簡單統一場論是局部可重正的,用微分幾何的話說,在切空間的一個鄰域內是可以重正的。註意,簡單統一場論是一次量子化的,所以可重正性並不是必須的,但局部可重正化意謂著在微擾論的框架下理論可以跑得更遠,可以計算出一階或二階以上微擾引出的修正,所以還是有實際意義的。
引力還有整體性質,僅有局部重正化是不夠的。原因在於,規範場論中的眾粒子生活在一個“眾生平等”的“民主社會”裏,所以局部重正化就等於整體重正化;而引力中的眾粒子還可以生成復合狀態,像是生活在一個“弱肉強食”的“集權社會”裏。另一方面,引力荷不是一個拓撲整數,二次量子化時不是一個好的量子數;所以只有當證明了引力在整體上是超可重正化以後“復雜”統一場論才是真正自洽的。
看起來真的如馬德西納(Maldcena)猜測的那樣,五維反de-Sitter空間中,量子引力與規範場論是對偶的。不過與空中樓閣式的馬德西納理論不同,我們的理論是腳踏實地的;我們認為愛因斯坦的質能關系式反映的是隱藏在對稱性背後的對偶性,這有些間接的證據,例如強子的質量譜近似地成一種線性的關系。從質能對偶性出發,就可以得出量子引力可能與強力對偶的關系,前提是強力的根源必須是能量,而強力看起來確實是能量引出的,比如具有比約肯標度不變性。
我們還是從Weyl引入規範場最初的原理出發,證明簡單統一場論確實是自洽的。考慮平面叢,由平面到平面的變換是10參數的群,當底流形為洛倫茲流形時,這個變換群與洛倫茲群是同構的。平面與平面之間可以定義聯絡和曲率式,當底流形為洛倫茲流形時,我們知道這正是電磁場的聯絡,詳細的證明可以參見陳省身老先生的演講。
簡單統一場論滿足可重正化最重要的條件,當實施一個標度變換後,與電荷一樣,引力荷沒有發生變化,感覺簡單統一場論應當是可以重正化的,但這需要一個嚴格的證明。
這裏,重正化的意思是簡單統一場論是局部可重正的,用微分幾何的話說,在切空間的一個鄰域內是可以重正的。註意,簡單統一場論是一次量子化的,所以可重正性並不是必須的,但局部可重正化意謂著在微擾論的框架下理論可以跑得更遠,可以計算出一階或二階以上微擾引出的修正,所以還是有實際意義的。
引力還有整體性質,僅有局部重正化是不夠的。原因在於,規範場論中的眾粒子生活在一個“眾生平等”的“民主社會”裏,所以局部重正化就等於整體重正化;而引力中的眾粒子還可以生成復合狀態,像是生活在一個“弱肉強食”的“集權社會”裏。另一方面,引力荷不是一個拓撲整數,二次量子化時不是一個好的量子數;所以只有當證明了引力在整體上是超可重正化以後“復雜”統一場論才是真正自洽的。
看起來真的如馬德西納(Maldcena)猜測的那樣,五維反de-Sitter空間中,量子引力與規範場論是對偶的。不過與空中樓閣式的馬德西納理論不同,我們的理論是腳踏實地的;我們認為愛因斯坦的質能關系式反映的是隱藏在對稱性背後的對偶性,這有些間接的證據,例如強子的質量譜近似地成一種線性的關系。從質能對偶性出發,就可以得出量子引力可能與強力對偶的關系,前提是強力的根源必須是能量,而強力看起來確實是能量引出的,比如具有比約肯標度不變性。
對偶性
射影空間沒有直觀的角度和距離的概念,實際上我們的構造中已經隱含了定義角度和距離所需的元素。弦論離不開超對稱性,因為引力子的自旋為2,必須有一個將玻色子轉換為費米子再轉換回玻色子的操作;而在量子細胞場論中,荷是空間的無窮遠點,在射影空間中無窮遠點與普通的點沒有什麽區別,只需簡單的直射變換就可以將無窮遠點變成普通點。
由拉蓋爾公式可以知道直射變換構成的群是SO(2)群,同構於電磁場的規範群U(1)群,對的!但拉蓋爾公式將荷變換到對偶荷形成的角度是180度,有問題的! 我們知道電磁場的波函數在轉過了360度後能夠保持不變。當然我們已經知道答案了,就是引進對偶的磁場,在射影空間中就相當於用對射變換代替簡單的直射變換,並且群的性質並沒有被破壞,對射變換構成的群稱為廣義射影變換群;在廣義射影變換群作用下,電磁場波函數轉過360度保持不變。
引力子的自旋為2,在轉過了180度後波函數不變;可見引力荷必須同時帶有引力電荷與引力磁荷,這樣轉過180度後,引力電荷變成引力磁荷,而引力磁荷變換為引力電荷。對於低速運動的有質量的物體,吸引力主要是引力電荷引起的,可以得到牛頓引力論的結果;對於光線,引力電荷與引力磁荷同時發揮作用,需要將橢圓幾何中的對徑點等同起來,所以太陽引起的光線偏折是牛頓引力論計算出的結果的2倍。我們看到,在低能區量子細胞場論與廣義相對論的結果是一致的。量子細胞場論改變的是對引力在高能區的看法,廣義相對論在高能區的結論是病態的,實際上弦論改變的也是對高能區的看法,但弦論的問題是不能確定在低能區與廣義相對論的對應關系。
現在我們知道為什麽自然界中沒有無質量的標量粒子了,由對偶性導出的標量粒子總是被隱藏在對稱性當中;在電磁場中,標量光子總是被隱藏在矢量光子中,這相當於Gupta-Bleuler量子化方法,但Gupta-Bleuler在數學上很復雜,而量子細胞場論用到的數學要簡單得多。在量子細胞場論中,自旋為1的縱向分量有點像鐵環,而自旋為0的縱向分量像是鐵環滾過的路,鐵環滾過路面,它們的縱向分量有一部分恰好是抵消的,剩余的部分就是庫侖力,只是自旋為0的縱向分量構成的路面只為鐵環本身而存在,這是狹義相對論的基本原理。Gupta-Bleuler需要使用不定度規,這本質上還是一種歐氏空間思想的殘余,而在量子細胞場論的射影叢中,本質上各個點都是平權的,就不需要使用不定度規了。
近代物理實驗有證據表明,在高能區,四種基本力的跑動耦合常數也可能會相交於一點,也就是說,可能有一個統一的耦合常數;不過我們不打算深究這個問題,還是暫時留給量子場論專家們傷腦筋吧。我們看到,由電磁力到電弱力到引力,在量子細胞場論中,大自然的四種基本力呈現出一種等級結構,在這方面,它們的確是統一的;電磁力是一種保持退化點x=0不變的力,弱力是一種保持二級退化曲線x±iy=0的力,引力是一種保持絕對型x2+y2=0不變的力,前一種力是後一種的退化情形。
說到對偶性,量子細胞場論完全可以稱為對偶場論,不過量子細胞是我們邏輯推理過程中重要的路標,能夠提供我們物理上直觀的圖像,一旦我們獲得一個數學上等價的描述,就可以將路標拿掉。回到電弱統一理論,對稱性生成了一個自旋為1的無質量矢量粒子,對偶性給出了一個自旋為0的標量粒子,那麽規範玻色子是如何吃進標量粒子而獲得質量的呢?答案還是在對偶性,對於低速運動的電荷,電場也就是電力線是像刺猬一樣布滿整個三維空間中的,假如我們強迫電荷以光速運動,那麽電場就緊縮到與運動方向垂直的一個平面上,相應的圖像在很多電動力學的教科書上都可以找到。
射影空間中還有點面對偶性,在洛倫茲群作用下可以保持質心荷不變,就樣就形成了一個平面叢;量子場論中,自旋為1的粒子自由自在的旋轉,沒有圓心的概念,用量子場論的話說,自旋只能取值1或者-1;加進了點線對偶性後,我們發現,量子細胞場論中自旋為1的粒子可以圍繞一個由對偶性生成的圓心旋轉,這樣就將無質量的標量粒子吃掉了。量子細胞場論中,光子具有三個分量;而在量子場論中,光子只有兩個分量,要麽使用洛侖茲規範,要麽使用庫侖規範;量子細胞場論中我們將洛侖茲規範和庫侖規範有機地組合在了一起,量子場論中似乎會把所有事情弄糟的鬼粒子在量子細胞場論中也不必出現了。對於電弱統一理論,由非對易幾何可以得知中間矢量玻色子的質量不過是一種“電弱磁”效應,根本不需要Higgs粒子的參與;由對稱性原理出發的量子場論無法導出類似的結論,量子細胞場論可以得出與非對易幾何類似的結論,但我們的推理很簡單,非對易幾何用到的數學非常復雜,估計會嚇退很多希望投身於統一場論研究的人。
回想地心說時代,人們發現很多星星的觀測軌道與理論不符,只能加進一個一個的本輪試圖自圓其說,到了哥白尼時代,開普勒發現行星的軌道可以不必是圓,還可以是橢圓。酉模仿射變換具有保持平行性和面積不變的特點,在相當於開普勒行星運動第二定律。假如我們允許中間矢量玻色子也可以沿橢圓旋轉,質量隙就自然地顯現出來;再者,如果玻色子的軌道是拋物線型的,就可以解釋弱相互作用下的CP破缺問題。不過量子細胞場論中不需要一個充滿Higgs粒子的背景場,點線對偶性引出的光子的縱向極化分量滿足的方程類似於聲波的方程,所以我們也可以將量子細胞場論中的標量光子稱為聲子,不過這和量子場論中的聲子有一個很大的不同,量子場論中的聲子屬於集體激發模式,也稱為元激發,需要一個背景場的參與;而量子細胞場論的聲子完全是由狹義相對論基本假設引出的,屬於場的基態;之所以產生這種差別的原因在於,量子場論中的閔可夫斯坦空間是不完備的,而量子細胞場論中的愛因斯坦空間是完備的。
這樣我們就給出了一個質量隙起源的較完美的答案,不要小看這個問題,它與龐加萊猜想、NP完全問題等並列稱為二十世紀七大難題之一,美國的克雷數學研究所對每個問題分別懸賞100萬美金。想當年劉維爾洋洋灑灑地寫了幾十頁紙終於證明了零基定理,不料被Hilbert短短的幾名話就重新證明了,劉維爾不無感慨地說:“這不是數學,是神學!”現在的問題是假如我們是對的,我們這種看似“神學”的證明是否應該得到那100萬美金的懸賞?
由拉蓋爾公式可以知道直射變換構成的群是SO(2)群,同構於電磁場的規範群U(1)群,對的!但拉蓋爾公式將荷變換到對偶荷形成的角度是180度,有問題的! 我們知道電磁場的波函數在轉過了360度後能夠保持不變。當然我們已經知道答案了,就是引進對偶的磁場,在射影空間中就相當於用對射變換代替簡單的直射變換,並且群的性質並沒有被破壞,對射變換構成的群稱為廣義射影變換群;在廣義射影變換群作用下,電磁場波函數轉過360度保持不變。
引力子的自旋為2,在轉過了180度後波函數不變;可見引力荷必須同時帶有引力電荷與引力磁荷,這樣轉過180度後,引力電荷變成引力磁荷,而引力磁荷變換為引力電荷。對於低速運動的有質量的物體,吸引力主要是引力電荷引起的,可以得到牛頓引力論的結果;對於光線,引力電荷與引力磁荷同時發揮作用,需要將橢圓幾何中的對徑點等同起來,所以太陽引起的光線偏折是牛頓引力論計算出的結果的2倍。我們看到,在低能區量子細胞場論與廣義相對論的結果是一致的。量子細胞場論改變的是對引力在高能區的看法,廣義相對論在高能區的結論是病態的,實際上弦論改變的也是對高能區的看法,但弦論的問題是不能確定在低能區與廣義相對論的對應關系。
現在我們知道為什麽自然界中沒有無質量的標量粒子了,由對偶性導出的標量粒子總是被隱藏在對稱性當中;在電磁場中,標量光子總是被隱藏在矢量光子中,這相當於Gupta-Bleuler量子化方法,但Gupta-Bleuler在數學上很復雜,而量子細胞場論用到的數學要簡單得多。在量子細胞場論中,自旋為1的縱向分量有點像鐵環,而自旋為0的縱向分量像是鐵環滾過的路,鐵環滾過路面,它們的縱向分量有一部分恰好是抵消的,剩余的部分就是庫侖力,只是自旋為0的縱向分量構成的路面只為鐵環本身而存在,這是狹義相對論的基本原理。Gupta-Bleuler需要使用不定度規,這本質上還是一種歐氏空間思想的殘余,而在量子細胞場論的射影叢中,本質上各個點都是平權的,就不需要使用不定度規了。
近代物理實驗有證據表明,在高能區,四種基本力的跑動耦合常數也可能會相交於一點,也就是說,可能有一個統一的耦合常數;不過我們不打算深究這個問題,還是暫時留給量子場論專家們傷腦筋吧。我們看到,由電磁力到電弱力到引力,在量子細胞場論中,大自然的四種基本力呈現出一種等級結構,在這方面,它們的確是統一的;電磁力是一種保持退化點x=0不變的力,弱力是一種保持二級退化曲線x±iy=0的力,引力是一種保持絕對型x2+y2=0不變的力,前一種力是後一種的退化情形。
說到對偶性,量子細胞場論完全可以稱為對偶場論,不過量子細胞是我們邏輯推理過程中重要的路標,能夠提供我們物理上直觀的圖像,一旦我們獲得一個數學上等價的描述,就可以將路標拿掉。回到電弱統一理論,對稱性生成了一個自旋為1的無質量矢量粒子,對偶性給出了一個自旋為0的標量粒子,那麽規範玻色子是如何吃進標量粒子而獲得質量的呢?答案還是在對偶性,對於低速運動的電荷,電場也就是電力線是像刺猬一樣布滿整個三維空間中的,假如我們強迫電荷以光速運動,那麽電場就緊縮到與運動方向垂直的一個平面上,相應的圖像在很多電動力學的教科書上都可以找到。
射影空間中還有點面對偶性,在洛倫茲群作用下可以保持質心荷不變,就樣就形成了一個平面叢;量子場論中,自旋為1的粒子自由自在的旋轉,沒有圓心的概念,用量子場論的話說,自旋只能取值1或者-1;加進了點線對偶性後,我們發現,量子細胞場論中自旋為1的粒子可以圍繞一個由對偶性生成的圓心旋轉,這樣就將無質量的標量粒子吃掉了。量子細胞場論中,光子具有三個分量;而在量子場論中,光子只有兩個分量,要麽使用洛侖茲規範,要麽使用庫侖規範;量子細胞場論中我們將洛侖茲規範和庫侖規範有機地組合在了一起,量子場論中似乎會把所有事情弄糟的鬼粒子在量子細胞場論中也不必出現了。對於電弱統一理論,由非對易幾何可以得知中間矢量玻色子的質量不過是一種“電弱磁”效應,根本不需要Higgs粒子的參與;由對稱性原理出發的量子場論無法導出類似的結論,量子細胞場論可以得出與非對易幾何類似的結論,但我們的推理很簡單,非對易幾何用到的數學非常復雜,估計會嚇退很多希望投身於統一場論研究的人。
回想地心說時代,人們發現很多星星的觀測軌道與理論不符,只能加進一個一個的本輪試圖自圓其說,到了哥白尼時代,開普勒發現行星的軌道可以不必是圓,還可以是橢圓。酉模仿射變換具有保持平行性和面積不變的特點,在相當於開普勒行星運動第二定律。假如我們允許中間矢量玻色子也可以沿橢圓旋轉,質量隙就自然地顯現出來;再者,如果玻色子的軌道是拋物線型的,就可以解釋弱相互作用下的CP破缺問題。不過量子細胞場論中不需要一個充滿Higgs粒子的背景場,點線對偶性引出的光子的縱向極化分量滿足的方程類似於聲波的方程,所以我們也可以將量子細胞場論中的標量光子稱為聲子,不過這和量子場論中的聲子有一個很大的不同,量子場論中的聲子屬於集體激發模式,也稱為元激發,需要一個背景場的參與;而量子細胞場論的聲子完全是由狹義相對論基本假設引出的,屬於場的基態;之所以產生這種差別的原因在於,量子場論中的閔可夫斯坦空間是不完備的,而量子細胞場論中的愛因斯坦空間是完備的。
這樣我們就給出了一個質量隙起源的較完美的答案,不要小看這個問題,它與龐加萊猜想、NP完全問題等並列稱為二十世紀七大難題之一,美國的克雷數學研究所對每個問題分別懸賞100萬美金。想當年劉維爾洋洋灑灑地寫了幾十頁紙終於證明了零基定理,不料被Hilbert短短的幾名話就重新證明了,劉維爾不無感慨地說:“這不是數學,是神學!”現在的問題是假如我們是對的,我們這種看似“神學”的證明是否應該得到那100萬美金的懸賞?
“烏雲”消散了!?
洛倫茲群是酉模仿射群,仿射空間是不完備的,連歐氏空間中最簡單的圓都無法定義;但歐氏空間中有討厭的絕對原點,就是本性奇點;返回到射影空間,我們又可以定義圓了。歐氏空間是內積空間,量子力學需要內積的概念,因為Hilbert空間是內積空間;量子場論也需要內積的概念,因為量子場論中最基本的不變自由拉格朗日量是場強張量與對偶場強張量的內積。非對易幾何引入了一大堆數學概念,最終找回了內積空間,而量子細胞場論中內積是很自然地定義的;如果非對易幾何的創始人Alain孔涅知道了量子細胞場論中如此簡單地推導出了內積的概念,一定也會感慨“神學”的威力吧!
引力的自由拉格朗日量是引力場強張量與對偶引力場強張量的內積,由於引力場強張量產生的是正確的愛因斯坦引力論,那麽對偶引力場強張量產生的力一定是排斥性的反引力,這就解釋了宇宙中為什麽會有暗能量的存在。這也說明了愛因斯坦引力論的局限性,因為廣義相對論不是一種規範理論,這與規範場論的中心思想是互相抵觸的,所以正確的引力論一定是愛因斯坦-cartan引力論。
考慮一下強力,誇克等價於量子細胞,量子細胞通過交換膠子產生相互作用,在這一點上量子細胞場論與量子色動力學的觀點是一致的。我們說愛因斯坦的質能關系式反映的實際上是一種隱藏在對稱性背後的質能對偶性,我們將高能區的核子比喻為雞蛋,將低能區的核子比喻為已經孵化成型的小雞;在高能區,誇克主要由能量構成,它們之間是漸近自由的,在低能區,誇克主要由質量構成,它們之間的相互作用力會很大;這一點上量子細胞場論與量子色動力學仍然是一致的。
對偶的學名是正交補,熟悉量子邏輯的人一定知道,量子邏輯的學名應當是正交補邏輯。當由對稱性產生對偶性時,對稱性破損了;在射影空間中洛倫茲空間是對稱的,但當映射到仿射空間中時,費米子一定要取三個空間方向之一,所以誇克可以是無色的,只要空間量子化就夠了;我們還要加上一個遞歸條件,這不是一個很強的限制,就好比一隊士兵聽到齊步走的命令後以統一的相位運動,這不是很難做到的;但這樣誇克的分布變得有規則起來,相鄰的誇克必然是反平行的,這樣空間就超導化了;量子色動力學中的重正化群只能給出一維的重正化流,量子細胞場論中核子可以有三維的結構;Yang-Mills場是非線性的,線性化的代價是核子的質量有一個上限,這個有限的質量正是色禁閉現象的根源。
這不正是特Hooft關於色禁閉猜想的最佳答案麽? 量子細胞場論中的二次量子化已經隱含了遞歸條件,所以一切的推導都是自然的;Seiberg-Witten理論也可以給出類似的答案,代價是必須引入無法證實的超對稱性和一大堆復雜的數學。並且量子細胞場論中的核子呈現出飽和性,這與核子物理的液滴模型和MIT袋模型的看法是一致的。我們還附帶地解決了一個古老的先有雞還是先有蛋的問題,雞和蛋是相互對偶的場,如果你去測量核子的話,得到的只能是雞和蛋的一個混合態。不引進任何外來的誇克質量,量子色動力學能夠給出核子質量的絕大部分,不過,由於它只能給出核子質量的93%,因此只能粗略地給它打93分;現在量子細胞場論中由於對稱性破損使圓變成橢圓,誇克獲得了質量,能打到100分了。
盡管粒子物理標準模型和帶暴脹的宇宙學大爆炸模型的建立表明基本物理規律的研究已取得了極其輝煌的成就,但仍然存在著不少極其重大的未解決的問題。在今天,在基本物理研究的天空中,究竟存在著哪些重要的“烏雲”呢?李政道教授在2000年國際弦理論會議上的講演中提出了四大問題:一、宇宙的暗能量和暗物質問題。二、引力的量子化問題。三、色禁閉問題。四、自然界是否存在著更大的對稱及更基本的統一理論。我們看到李政道教授提出的四大問題在量子細胞場論中都得到了圓滿的解答。
引力的自由拉格朗日量是引力場強張量與對偶引力場強張量的內積,由於引力場強張量產生的是正確的愛因斯坦引力論,那麽對偶引力場強張量產生的力一定是排斥性的反引力,這就解釋了宇宙中為什麽會有暗能量的存在。這也說明了愛因斯坦引力論的局限性,因為廣義相對論不是一種規範理論,這與規範場論的中心思想是互相抵觸的,所以正確的引力論一定是愛因斯坦-cartan引力論。
考慮一下強力,誇克等價於量子細胞,量子細胞通過交換膠子產生相互作用,在這一點上量子細胞場論與量子色動力學的觀點是一致的。我們說愛因斯坦的質能關系式反映的實際上是一種隱藏在對稱性背後的質能對偶性,我們將高能區的核子比喻為雞蛋,將低能區的核子比喻為已經孵化成型的小雞;在高能區,誇克主要由能量構成,它們之間是漸近自由的,在低能區,誇克主要由質量構成,它們之間的相互作用力會很大;這一點上量子細胞場論與量子色動力學仍然是一致的。
對偶的學名是正交補,熟悉量子邏輯的人一定知道,量子邏輯的學名應當是正交補邏輯。當由對稱性產生對偶性時,對稱性破損了;在射影空間中洛倫茲空間是對稱的,但當映射到仿射空間中時,費米子一定要取三個空間方向之一,所以誇克可以是無色的,只要空間量子化就夠了;我們還要加上一個遞歸條件,這不是一個很強的限制,就好比一隊士兵聽到齊步走的命令後以統一的相位運動,這不是很難做到的;但這樣誇克的分布變得有規則起來,相鄰的誇克必然是反平行的,這樣空間就超導化了;量子色動力學中的重正化群只能給出一維的重正化流,量子細胞場論中核子可以有三維的結構;Yang-Mills場是非線性的,線性化的代價是核子的質量有一個上限,這個有限的質量正是色禁閉現象的根源。
這不正是特Hooft關於色禁閉猜想的最佳答案麽? 量子細胞場論中的二次量子化已經隱含了遞歸條件,所以一切的推導都是自然的;Seiberg-Witten理論也可以給出類似的答案,代價是必須引入無法證實的超對稱性和一大堆復雜的數學。並且量子細胞場論中的核子呈現出飽和性,這與核子物理的液滴模型和MIT袋模型的看法是一致的。我們還附帶地解決了一個古老的先有雞還是先有蛋的問題,雞和蛋是相互對偶的場,如果你去測量核子的話,得到的只能是雞和蛋的一個混合態。不引進任何外來的誇克質量,量子色動力學能夠給出核子質量的絕大部分,不過,由於它只能給出核子質量的93%,因此只能粗略地給它打93分;現在量子細胞場論中由於對稱性破損使圓變成橢圓,誇克獲得了質量,能打到100分了。
盡管粒子物理標準模型和帶暴脹的宇宙學大爆炸模型的建立表明基本物理規律的研究已取得了極其輝煌的成就,但仍然存在著不少極其重大的未解決的問題。在今天,在基本物理研究的天空中,究竟存在著哪些重要的“烏雲”呢?李政道教授在2000年國際弦理論會議上的講演中提出了四大問題:一、宇宙的暗能量和暗物質問題。二、引力的量子化問題。三、色禁閉問題。四、自然界是否存在著更大的對稱及更基本的統一理論。我們看到李政道教授提出的四大問題在量子細胞場論中都得到了圓滿的解答。
對偶性的結果
由於狹義相對論是愛爾朗根綱領的一個特例,Felix Klein(不是弦論中的Klein,更不是編寫〈古今數學思想〉那個Klein)成了狹義相對論最早和最堅定的支持者。1974年,楊振寧明白了規範場是標架叢上的聯絡;於是,陳省身認為統一場論的基礎一定是這些幾何上的數學概念。沿著這些數學思想發展,我們將Klein幾何與矢量叢的概念結合在了一起,發現果然是碩果累累。我們在沒有引入任何新的假設的前提下用幾何的語言重寫了量子場論,我們唯一的假定是統一場論一定是很美的,也就是空間一定是完備的。
對於引力而言,如果引力滿足規範對稱性,就會演變到愛因斯坦-cartan引力論,我們對自旋聯絡量子化,發現引力必定滿足超泡利不相容原理,這就解決了奇點問題。引力場必定是一種自對偶的場,這相當於M理論中的S對偶性,用S對偶性可以解釋暗能量問題,因此如果M理論可能是對的,量子細胞引力論就一定是對的。其實廣義相對論的問題不止有宇宙學難題,太陽系所處的銀河系是一種旋臂結構,這用廣義相對論和弦論都是無法解釋的,量子細胞引力論有可能解決這個問題,但這需要有一個嚴格的證明。
量子場論中的對稱性自發破損一詞有誤導的成份,我們知道對稱性自發破損等價於量子細胞場論中的點線對偶性,對於電弱統一理論而言,手征對稱性破損之後是不需要恢復的,而對於量子色動力學而言手征對稱性破損之後的自發恢復至關重要;迄今為止,尚未有人能夠給出手征對稱性自發破缺的數學證明,但從這一破缺方式已經得到了大量的間接證據;這在量子細胞場論中根本就不是一個問題,我們不僅很容易證明手征對稱性的自發破缺,而且還很容易導出手征對稱性破缺之後的恢復機制,它們不過是遞歸條件而已。量子色動力學對π 介子及其它假Goldstone 粒子質量的計算雖然很漂亮,但從回答本原問題的角度看卻仍不足以令人滿意;量子色動力學為質量起源問題提供了一個獨特而接近完美的回答,為了尋找更接近滿分的答案,我們不得不重新回到標準模型中不能約化的那些質量上來。那些質量究竟來自何方?究竟還能不能約化?這些問題的答案只能從量子細胞場論中尋找了。
廣義相對論中的引力耦合常數是有量綱的,可以預計的是廣義相對論在高能區的行為一定是不好的,弦論改善的是在普朗克尺度下引力論的奇異行為,弦論回避了量子場論中的重正化方法,但這也使弦論與量子場論的兼容性打了折扣。費曼稱量子場論的重正化方法是一種“腦筋不正常的運轉”,但是這種“將垃圾掃到地氈下藏起來”的做法實際上是對的,並獲得了物理實驗的支持。量子細胞場論直面了重正化的問題,量子場論中的標度行為涉及到的群是共形群,生成元是一種稱為伸縮子的東西;仿射空間中也有伸縮子,牽涉到的變換群稱為相似變換群;實際上Weyl在最初的規範場論中用的正是相似變換群。
由點線對偶性生成的是規範場的縱向極化分量,在量子場論中規範場的縱向極化是不需要重整化的。由相似變換群生成的規範場卻需要小心處理,一方面相似變換違反量子力學中波函數的歸一化要求,這也是Weyl最初的想法被拋棄的原因,這在量子細胞場論中是不難處理的,我們處理的是在空間中每一點上定義的纖維叢,只要伸與縮是對偶的就可以解決波函數歸一化問題;另一方面,生成引力的是保持一對絕對對合點不變的變換群,正是相似變換群。看來Weyl最初的想法並非一無是處,只是用錯了地方。
對於引力而言,如果引力滿足規範對稱性,就會演變到愛因斯坦-cartan引力論,我們對自旋聯絡量子化,發現引力必定滿足超泡利不相容原理,這就解決了奇點問題。引力場必定是一種自對偶的場,這相當於M理論中的S對偶性,用S對偶性可以解釋暗能量問題,因此如果M理論可能是對的,量子細胞引力論就一定是對的。其實廣義相對論的問題不止有宇宙學難題,太陽系所處的銀河系是一種旋臂結構,這用廣義相對論和弦論都是無法解釋的,量子細胞引力論有可能解決這個問題,但這需要有一個嚴格的證明。
量子場論中的對稱性自發破損一詞有誤導的成份,我們知道對稱性自發破損等價於量子細胞場論中的點線對偶性,對於電弱統一理論而言,手征對稱性破損之後是不需要恢復的,而對於量子色動力學而言手征對稱性破損之後的自發恢復至關重要;迄今為止,尚未有人能夠給出手征對稱性自發破缺的數學證明,但從這一破缺方式已經得到了大量的間接證據;這在量子細胞場論中根本就不是一個問題,我們不僅很容易證明手征對稱性的自發破缺,而且還很容易導出手征對稱性破缺之後的恢復機制,它們不過是遞歸條件而已。量子色動力學對π 介子及其它假Goldstone 粒子質量的計算雖然很漂亮,但從回答本原問題的角度看卻仍不足以令人滿意;量子色動力學為質量起源問題提供了一個獨特而接近完美的回答,為了尋找更接近滿分的答案,我們不得不重新回到標準模型中不能約化的那些質量上來。那些質量究竟來自何方?究竟還能不能約化?這些問題的答案只能從量子細胞場論中尋找了。
廣義相對論中的引力耦合常數是有量綱的,可以預計的是廣義相對論在高能區的行為一定是不好的,弦論改善的是在普朗克尺度下引力論的奇異行為,弦論回避了量子場論中的重正化方法,但這也使弦論與量子場論的兼容性打了折扣。費曼稱量子場論的重正化方法是一種“腦筋不正常的運轉”,但是這種“將垃圾掃到地氈下藏起來”的做法實際上是對的,並獲得了物理實驗的支持。量子細胞場論直面了重正化的問題,量子場論中的標度行為涉及到的群是共形群,生成元是一種稱為伸縮子的東西;仿射空間中也有伸縮子,牽涉到的變換群稱為相似變換群;實際上Weyl在最初的規範場論中用的正是相似變換群。
由點線對偶性生成的是規範場的縱向極化分量,在量子場論中規範場的縱向極化是不需要重整化的。由相似變換群生成的規範場卻需要小心處理,一方面相似變換違反量子力學中波函數的歸一化要求,這也是Weyl最初的想法被拋棄的原因,這在量子細胞場論中是不難處理的,我們處理的是在空間中每一點上定義的纖維叢,只要伸與縮是對偶的就可以解決波函數歸一化問題;另一方面,生成引力的是保持一對絕對對合點不變的變換群,正是相似變換群。看來Weyl最初的想法並非一無是處,只是用錯了地方。
Yang-Mills理論與質量隙猜想(Mass Gap Hypothesis)
物理始終是新數學理論之靈感與動力的來源,自微積分的發展歷史以來,好的數學一直是受物理之激勵才有更好的發展,物理中產生的數學問題解答及方法,從過去到現在,一直是數學活力的來源。物理在某種意義底下提供了數學最深刻的應用。Yang-Mills 方程起源於量子物理,是由著名華裔物理學家,諾貝爾獎得主楊振寧與 Robert Mills所發現。
我們說物理定律是“對稱的”,意思是我們可以對物理定律或者對我們表達物理定律的方式做一些事,結果沒有任何差異。對稱說明了那些沒有改變或不能發生的事,所以對稱是現代物理學的動力。德國數學家 Hermann Weyl (1885-1955)給對稱(symmetry)下了一個絕佳的定義:「假如你對某件事物做了某些事情(operation)之後,它看起來和原來完全相同,那麽它就是對稱的。」在數學中常常把不變性(invariance)稱為對稱性。Hermann Weyl 曾說: 「我的研究工作嘗試把真理與美統一起來,可是如果要我在兩者之中擇一的話,通常我都選擇美。」其實他心中的美就是對稱。當數學應用到物理時,美學判斷的有效性最為可觀。數學家在他們的研究中,受到結構美之概念形式的強烈期望所驅使,是相當平常的。
早年把「對稱性、不變性及守恒量之間最關鍵的聯系」結晶成形,為愛因斯坦發展廣義相對論鋪路的是德國女性數學家Emmy Noether (1882-1935)。在廣義相對論發展之初,人們發覺(表面上看來)在彎曲的四維空間中,能量是不守恒的,這是一個理論基礎上的缺陷。Noether把這問題解決了,她利用對稱性證明彎曲的四維空間之能量是守恒的。對她而言,把對稱性與基本自然律聯系在一起的理念是非常自然的Noether對於對稱性與自然律的構想,給了美與真理之間一個最具體的鏈接。科學裏認為的美,與貝多芬音樂中的美是同樣的東西!
基礎物理發現的第一個重要的對稱性是Lorentz 不變性(經Lorentz 變換後不變)。這是作為Maxwell 方程的數學性質而被發現的。愛因斯坦就是以Lorentz變換為基礎而發現狹義相對論,後來再加以推廣,由廣義坐標不變性的想法,加上等價原理,導致了廣義相對論。對稱性也導致英國物理學家諾貝爾物理獎得主P. Dirac (1902-1984)把狹義相對論與量子力學以數學方法合並在一起後(量子場論),預測反物質的存在。這後來是由美國加州理工學院的安德森由實驗證實,並因此榮獲諾貝爾物理獎。因此藉由對稱性可以幫助我們〝看〞到物理現象,從此就不在黑暗中摸索。
早在二十世紀初(1918-1919) H. Weyl為著討論電磁力與引力之對稱關系,提出所謂“規範不變性”(gauge invariance)之概念,但是要到 1954 年楊振寧與 R. Mills 提出的“Yang-Mills 規範理論”,才是真正的突破。楊振寧由數學入手,提出一個規範性的理論架構,後來逐漸發展成為量子物理最重要的理論之一,也使得他成為替近代物理奠基的一代大師人物。
楊振寧與 R. Mills提出的理論,會產生傳送作用力的粒子,但是他們碰到的困難是無法解決這個粒子的質量的問題。他們從數學推導的結果是,這個粒子有電荷但沒有質量。因此困難是如果這一有電荷的粒子是沒有質量,那麽為什麽沒有任何實驗證據呢?而如果假定有質量,規範對稱性就會被破壞。一般物理學家是相信有質量,因此如何填補這個漏洞(gap)就是深具挑戰性的數學問題。
規範場方程(Yang-Mills equation)是由電磁學的Maxwell方程而來。1974年楊振寧又發現了這些方程式與微分幾何大師陳省身研究纖維叢理論(fiber bundle theory)中的陳示性類(chern class) 有密切的關系。物理學者因而知道有了解陳示性類的必要。這實在是令人驚訝的地方。至於為什麽自然界的各種力都建築在幾何學中的纖維叢觀念上,始終是個未解之謎。
從歷史的發展而言數學滲入廣義相對論與規範場理論的過程是全然不同的。愛因斯坦沒有黎曼幾何(Riemann geometry)就不可能寫出廣義相對論方程式。就後者而言,規範場方程式早已寫出來了,但後來是透過數學才了解其深意。由於楊振寧的影響,Yang-Mills方程已向數學界滲透,並導致許多優美的數學成果特別是拓撲學(topology)的驚人突破,S. Donaldson為此榮獲1986年的費爾茲獎。另外則是英國數學家阿提亞( M. F. Atiyah)與美國數學家辛格( I. M. Singer)關於瞬子(instanton)即Yang-Mills方程的自對偶解的工作。
我們說物理定律是“對稱的”,意思是我們可以對物理定律或者對我們表達物理定律的方式做一些事,結果沒有任何差異。對稱說明了那些沒有改變或不能發生的事,所以對稱是現代物理學的動力。德國數學家 Hermann Weyl (1885-1955)給對稱(symmetry)下了一個絕佳的定義:「假如你對某件事物做了某些事情(operation)之後,它看起來和原來完全相同,那麽它就是對稱的。」在數學中常常把不變性(invariance)稱為對稱性。Hermann Weyl 曾說: 「我的研究工作嘗試把真理與美統一起來,可是如果要我在兩者之中擇一的話,通常我都選擇美。」其實他心中的美就是對稱。當數學應用到物理時,美學判斷的有效性最為可觀。數學家在他們的研究中,受到結構美之概念形式的強烈期望所驅使,是相當平常的。
早年把「對稱性、不變性及守恒量之間最關鍵的聯系」結晶成形,為愛因斯坦發展廣義相對論鋪路的是德國女性數學家Emmy Noether (1882-1935)。在廣義相對論發展之初,人們發覺(表面上看來)在彎曲的四維空間中,能量是不守恒的,這是一個理論基礎上的缺陷。Noether把這問題解決了,她利用對稱性證明彎曲的四維空間之能量是守恒的。對她而言,把對稱性與基本自然律聯系在一起的理念是非常自然的Noether對於對稱性與自然律的構想,給了美與真理之間一個最具體的鏈接。科學裏認為的美,與貝多芬音樂中的美是同樣的東西!
基礎物理發現的第一個重要的對稱性是Lorentz 不變性(經Lorentz 變換後不變)。這是作為Maxwell 方程的數學性質而被發現的。愛因斯坦就是以Lorentz變換為基礎而發現狹義相對論,後來再加以推廣,由廣義坐標不變性的想法,加上等價原理,導致了廣義相對論。對稱性也導致英國物理學家諾貝爾物理獎得主P. Dirac (1902-1984)把狹義相對論與量子力學以數學方法合並在一起後(量子場論),預測反物質的存在。這後來是由美國加州理工學院的安德森由實驗證實,並因此榮獲諾貝爾物理獎。因此藉由對稱性可以幫助我們〝看〞到物理現象,從此就不在黑暗中摸索。
早在二十世紀初(1918-1919) H. Weyl為著討論電磁力與引力之對稱關系,提出所謂“規範不變性”(gauge invariance)之概念,但是要到 1954 年楊振寧與 R. Mills 提出的“Yang-Mills 規範理論”,才是真正的突破。楊振寧由數學入手,提出一個規範性的理論架構,後來逐漸發展成為量子物理最重要的理論之一,也使得他成為替近代物理奠基的一代大師人物。
楊振寧與 R. Mills提出的理論,會產生傳送作用力的粒子,但是他們碰到的困難是無法解決這個粒子的質量的問題。他們從數學推導的結果是,這個粒子有電荷但沒有質量。因此困難是如果這一有電荷的粒子是沒有質量,那麽為什麽沒有任何實驗證據呢?而如果假定有質量,規範對稱性就會被破壞。一般物理學家是相信有質量,因此如何填補這個漏洞(gap)就是深具挑戰性的數學問題。
規範場方程(Yang-Mills equation)是由電磁學的Maxwell方程而來。1974年楊振寧又發現了這些方程式與微分幾何大師陳省身研究纖維叢理論(fiber bundle theory)中的陳示性類(chern class) 有密切的關系。物理學者因而知道有了解陳示性類的必要。這實在是令人驚訝的地方。至於為什麽自然界的各種力都建築在幾何學中的纖維叢觀念上,始終是個未解之謎。
從歷史的發展而言數學滲入廣義相對論與規範場理論的過程是全然不同的。愛因斯坦沒有黎曼幾何(Riemann geometry)就不可能寫出廣義相對論方程式。就後者而言,規範場方程式早已寫出來了,但後來是透過數學才了解其深意。由於楊振寧的影響,Yang-Mills方程已向數學界滲透,並導致許多優美的數學成果特別是拓撲學(topology)的驚人突破,S. Donaldson為此榮獲1986年的費爾茲獎。另外則是英國數學家阿提亞( M. F. Atiyah)與美國數學家辛格( I. M. Singer)關於瞬子(instanton)即Yang-Mills方程的自對偶解的工作。
相對論與幾何
對偶性是量子力學的基本假設,所謂正則量子化方法是指一對對偶的量,比如位置和動量算符的非對易算符;我們也知道,狹義相對論與量子力學是兼容的,這裏蘊含了量子細胞場論與經典量子場論的一個重要區別,量子細胞場論認為真空真的就是空的;量子場論中那些由真空產生的效應,例如Casimir效應完全可以由自對偶細胞完成;但這裏自對偶細胞只有局部的意義,不會擴散到整個真空。狹義相對論否認真空中存在背景場,量子場論是狹義相對論與量子力學相結合的產物,怎麽會出現一個無限大的真空呢?
從幾何的觀點來看,愛因斯坦引力之所以與其他力無法統一到一起的一個重要原因是,引力存在於一個彎曲的時空裏,而其他三種力存在於一個平直的時空中,而實際上這種傳統量子場論的觀點是有問題的;事實上從幾何的觀點看電磁力、弱力或強力也可以通過坐標變換,看成是彎曲時空幾何產生的力。如果我們將大自然的四種基本力從幾何的觀點放在同一個空間中一起考慮,就可以得到一些必然性的結論。
將有質量粒子與無質量粒子放到一起看,狹義相對論引出的空間等價於雙曲幾何,具體的論證可參見費保俊所著的《相對論與非歐幾何》一書,這樣引出的是斥力;而我們知道引力是吸引性的,所以橢圓幾何也是同時存在的;如何解決這個問題,回想費曼的觀點,一個沿正時間軸方向移動的粒子必然會有一個沿逆時間軸移動的粒子相對應,所以我們說量子細胞引力中,引力和斥力是同時存在的,這裏沿逆時間軸移動的粒子可以解釋成霍金所說的沿虛時間軸移動的粒子,只是虛時間軸與實時間軸是一對相伴隨的軸。
將有質量粒子與無質量粒子統一考慮,狹義相對論就否認了時空是平直的可能性,如果時空是平直的,那麽光速就應該是無限大,這與狹義相對論原則是矛盾的;之所以出現量子場論中時空平直的論調,是與閔可夫斯基平直的觀點相聯系的;回想一下,閔可夫斯基就是愛因斯坦上大學期間稱他為“懶狗”的那位數學教授,但愛因斯坦並沒有堅持時空的相對性原則,廣義相對論最終還是基於閔可夫斯基空間的。量子細胞場論也引出了一個問題,通過坐標變換現在四種力都是存在於彎曲時空中的,那與傳統量子場論是如何兼容的,其實量子細胞場論早已解決了這個問題;回想一下,點線對偶性給出的幾何就局部等價於平直的時空。
從幾何的觀點來看,愛因斯坦引力之所以與其他力無法統一到一起的一個重要原因是,引力存在於一個彎曲的時空裏,而其他三種力存在於一個平直的時空中,而實際上這種傳統量子場論的觀點是有問題的;事實上從幾何的觀點看電磁力、弱力或強力也可以通過坐標變換,看成是彎曲時空幾何產生的力。如果我們將大自然的四種基本力從幾何的觀點放在同一個空間中一起考慮,就可以得到一些必然性的結論。
將有質量粒子與無質量粒子放到一起看,狹義相對論引出的空間等價於雙曲幾何,具體的論證可參見費保俊所著的《相對論與非歐幾何》一書,這樣引出的是斥力;而我們知道引力是吸引性的,所以橢圓幾何也是同時存在的;如何解決這個問題,回想費曼的觀點,一個沿正時間軸方向移動的粒子必然會有一個沿逆時間軸移動的粒子相對應,所以我們說量子細胞引力中,引力和斥力是同時存在的,這裏沿逆時間軸移動的粒子可以解釋成霍金所說的沿虛時間軸移動的粒子,只是虛時間軸與實時間軸是一對相伴隨的軸。
將有質量粒子與無質量粒子統一考慮,狹義相對論就否認了時空是平直的可能性,如果時空是平直的,那麽光速就應該是無限大,這與狹義相對論原則是矛盾的;之所以出現量子場論中時空平直的論調,是與閔可夫斯基平直的觀點相聯系的;回想一下,閔可夫斯基就是愛因斯坦上大學期間稱他為“懶狗”的那位數學教授,但愛因斯坦並沒有堅持時空的相對性原則,廣義相對論最終還是基於閔可夫斯基空間的。量子細胞場論也引出了一個問題,通過坐標變換現在四種力都是存在於彎曲時空中的,那與傳統量子場論是如何兼容的,其實量子細胞場論早已解決了這個問題;回想一下,點線對偶性給出的幾何就局部等價於平直的時空。
量子細胞宇宙學模型
簡單統一場論
考慮一種背景為四維de Sitter時空與四維反de Sitter時空的乘積的宇宙學模型,有質量粒子存在於一個背景為正的常曲率de Sitter空間中,引力子則存在於反de Sitter時空中;de Sitter時空是封閉的,構成了一個四維超球面,同時這個四維超球面又構成了反de Sitter時空的邊界;我們知道反de Sitter時空中任何一點到達邊界的距離都是無窮遠,引力子是無質量的,只有無質量的粒子才能夠到達反de Sitter時空的邊界;引力子的測地線是反de Sitter時空中的圓弧線,這樣一個雙曲幾何的模型是龐加萊在研究自守函數時發現的。
在引力場的最小耦合中有一個系數i,眾所周知這個系數來自於量子力學,這個系數是愛因斯坦引力論中沒有的,卻是量子場論所必需的,這就意謂著有質量物體的場與引力子場是垂直的。這樣一個宇宙學模型很明顯有馬德西納猜想的影子,所以我們將兩個名字合在一起,稱這樣一個時空為馬德西特(Malde Sitter)時空。只是馬德西納猜想是個空中樓閣,而馬德西特時空卻是量子細胞引力論的一個很自然的推論;並且真實的宇宙很可能正是這樣構成的。我們似乎又回到了地心說時代,不過這是引入了牛頓引力論和愛因斯坦引力論中正確思想以後的現代版地心說。
考慮一個穩恒態的宇宙和牛頓引力,我們知道牛頓引力勢與粒子間的距離成反比,也就是與龐加萊雙曲模型中圓弧弦的半徑成反比;當距離很小時,量子細胞引力論引出的是牛頓引力的反平方律,可是隨著距離的增大,量子細胞引力論導出的引力勢呈單調下降的趨勢;當兩個粒子處於的位置位於橢圓幾何的對徑點上時,由於圓弧弦為直線,它的半徑為無窮大,這兩個粒子間的牛頓引力勢為0;假設我們位於宇宙的北極點上,考查位於宇宙南半球的兩個粒子之間的引力相互作用,它們之間確實存在的是引力,而相對我們而言存在的是斥力,這就解釋了為什麽離我們很遠的星系看起來在快速離我們而去,要知道引力對光線的偏折作用比對普通有質量物體的偏折作用大一倍,這樣就會產生強烈的引力紅移,所以離我們很遠的星系的紅移是引力引起的。
量子細胞引力論中有一個歐氏空間的原點,也就是三個空間坐標和一個時間坐標都為0的點,不過有質量的物體是不能到達坐標原點的,只有引力子能夠到達坐標原點,但引力子卻是借道而過,因為對引力子而言不存在靜止的參考系。在量子細胞引力論中,有質量物質場與引力子場遵守不同的場方程,而且黑洞與宇宙遵守的也是不同的幾何模型,即單重橢圓幾何與雙重橢圓幾何的差別,這是量子細胞引力論與廣義相對論的又一差別。黑洞是有質量的,一種可能是黑洞永遠無法到達坐標原點,除非黑洞變成一個巨型的引力子,才能從坐標原點借道而過,坐標原點永遠也不可能成為奇點;或者黑洞大到足以吞下整個宇宙,這在量子細胞引力論中意謂著這種黑洞是不穩定的,幾乎立刻就會反彈回去;所以如果宇宙是從大爆炸中誕生的,這不是從奇點上誕生的,宇宙有一個最小的體積,將整個宇宙壓縮到一個黑洞裏,不知道有沒有人計算過宇宙的最小體積是多少;這意謂著量子細胞宇宙不需要一個古思所說的暴漲階段。
還有一種可能是黑洞與宇宙是對偶的,黑洞會把橢圓幾何中的對徑點連接起來,從坐標原點借道而過,這就是廣義相對論引出的所謂蟲洞,這意謂著黑洞吸收的物質會從對徑點上噴發出來形成所謂的白洞;這就好比在地球上開鑿一個穿地心而過的隧道,從隧道的這頭扔一個東西下去,有可能從隧道的另外一頭也就是地球的另外一端重新冒出來;白洞有可能是我們觀測到的類星體,現在我們知道類星體很可能就是離我們並不遙遠的黑洞從宇宙的另外一端重新冒出來,所以類星體很亮,並且由於身處宇宙的另外一端,會伴隨著巨大的引力紅移。
在引力場的最小耦合中有一個系數i,眾所周知這個系數來自於量子力學,這個系數是愛因斯坦引力論中沒有的,卻是量子場論所必需的,這就意謂著有質量物體的場與引力子場是垂直的。這樣一個宇宙學模型很明顯有馬德西納猜想的影子,所以我們將兩個名字合在一起,稱這樣一個時空為馬德西特(Malde Sitter)時空。只是馬德西納猜想是個空中樓閣,而馬德西特時空卻是量子細胞引力論的一個很自然的推論;並且真實的宇宙很可能正是這樣構成的。我們似乎又回到了地心說時代,不過這是引入了牛頓引力論和愛因斯坦引力論中正確思想以後的現代版地心說。
考慮一個穩恒態的宇宙和牛頓引力,我們知道牛頓引力勢與粒子間的距離成反比,也就是與龐加萊雙曲模型中圓弧弦的半徑成反比;當距離很小時,量子細胞引力論引出的是牛頓引力的反平方律,可是隨著距離的增大,量子細胞引力論導出的引力勢呈單調下降的趨勢;當兩個粒子處於的位置位於橢圓幾何的對徑點上時,由於圓弧弦為直線,它的半徑為無窮大,這兩個粒子間的牛頓引力勢為0;假設我們位於宇宙的北極點上,考查位於宇宙南半球的兩個粒子之間的引力相互作用,它們之間確實存在的是引力,而相對我們而言存在的是斥力,這就解釋了為什麽離我們很遠的星系看起來在快速離我們而去,要知道引力對光線的偏折作用比對普通有質量物體的偏折作用大一倍,這樣就會產生強烈的引力紅移,所以離我們很遠的星系的紅移是引力引起的。
量子細胞引力論中有一個歐氏空間的原點,也就是三個空間坐標和一個時間坐標都為0的點,不過有質量的物體是不能到達坐標原點的,只有引力子能夠到達坐標原點,但引力子卻是借道而過,因為對引力子而言不存在靜止的參考系。在量子細胞引力論中,有質量物質場與引力子場遵守不同的場方程,而且黑洞與宇宙遵守的也是不同的幾何模型,即單重橢圓幾何與雙重橢圓幾何的差別,這是量子細胞引力論與廣義相對論的又一差別。黑洞是有質量的,一種可能是黑洞永遠無法到達坐標原點,除非黑洞變成一個巨型的引力子,才能從坐標原點借道而過,坐標原點永遠也不可能成為奇點;或者黑洞大到足以吞下整個宇宙,這在量子細胞引力論中意謂著這種黑洞是不穩定的,幾乎立刻就會反彈回去;所以如果宇宙是從大爆炸中誕生的,這不是從奇點上誕生的,宇宙有一個最小的體積,將整個宇宙壓縮到一個黑洞裏,不知道有沒有人計算過宇宙的最小體積是多少;這意謂著量子細胞宇宙不需要一個古思所說的暴漲階段。
還有一種可能是黑洞與宇宙是對偶的,黑洞會把橢圓幾何中的對徑點連接起來,從坐標原點借道而過,這就是廣義相對論引出的所謂蟲洞,這意謂著黑洞吸收的物質會從對徑點上噴發出來形成所謂的白洞;這就好比在地球上開鑿一個穿地心而過的隧道,從隧道的這頭扔一個東西下去,有可能從隧道的另外一頭也就是地球的另外一端重新冒出來;白洞有可能是我們觀測到的類星體,現在我們知道類星體很可能就是離我們並不遙遠的黑洞從宇宙的另外一端重新冒出來,所以類星體很亮,並且由於身處宇宙的另外一端,會伴隨著巨大的引力紅移。
簡單統一場論
在Klein以後,法國數學家龐加萊給出了雙曲幾何的另一種模型,它可以應用到復變函數論裏的一些重要結果的推論上;龐加萊模型仍然取圓的內部作用雙曲幾何的平面,卻把垂直於已知圓周的圓弧作為直線;算做移動的是把圓變成自己的任何保角變換。龐加萊雙曲幾何模型為我們討論統一場論提供了很好的平臺,我們知道,龐加萊雙曲幾何不僅可以建立在超球面的內部,也可以建立在上半平面上,上半平面上的雙曲幾何對應的正是電磁場。我們讓正電荷或負電荷沿上半平面的邊界活動,與邊界垂直的半圓弧是光子移動時的測地線,這裏有個小問題,光子在內部空間移動的速度不是光速c,而是要乘上一個系數π/2,好在經過量子力學的長期熏陶,人們已經習慣了在各種抽象空間之間變來變去,所以不必太操心這個系數。現在與邊界垂直的半圓弧的半徑的倒數正是庫侖勢,這樣利用龐加萊雙曲幾何模型我們有了一個電磁力和引力的統一幾何模型。
從這個模型出發可以導出很多有意義的結論,利用我們鐵環與路面的類比,我們知道在電磁場中位置和動量確實是對偶的場量;回想電磁場量子化的歷史,簡單地將電磁場量子化,人們發現與庫侖勢共軛的動量恒為零,於是才有了Gupta-Bleuler利用不定度規的量子化方法,細胞量子化方法與Gupta-Bleuler方法等價,並且提供了一個Gupta-Bleuler量子化方法的直觀的幾何模型。之所以選擇龐加萊模型是與射影空間的特定性質有關系的,當我們將射影空間改造成度量空間後,移動了多少距離和轉過了多少角度完全是對偶的概念;以引力為例,在de Sitter時空中即宇宙邊界上的移動與在內部的反de Sitter時空中轉過多少角度是對偶的。所以在量子細胞場論中,代表旋轉的自旋為1的矢量分量與代表移動的自旋為0的標量分量完全是對偶的不可能分割的整體;而在傳統量子場論中,這兩種分量是分開來處理的。
費曼稱量子電動力學中的無窮大是腦筋不正常的,從現實的角度出發我們也知道帶著量子場論中沒有物理意義的無窮大試圖構建統一場論也是一件不可能完成的任務。既然在量子細胞場論中,位置與動量是一對共軛的場量,而無窮遠點是位置的極限,無窮大是量子電動力學中動量的極限,可見最子細胞場論中的無窮遠與量子場論中的無窮大之間確實存在對偶關系;量子場論牽涉到無窮大的加減乘除運算,就目前人類已經掌握的數學知識體系而言,只有射影空間中的無窮遠是可以直接實施加減乘除運算的從而獲得邏輯上自洽的結果,所以從量子場論發展到量子細胞場論在邏輯上的必然的,所謂自古華山一條路,人類還沒有找到其它處理無窮的辦法。
從量子場論發展到量子細胞場論,腦筋終於正常了!以下為了討論的方便,我們將量子細胞場論中的愛因斯坦空間簡稱為理想世界,將量子場論中以閔可夫斯基空間為基底的物理世界稱為現實世界;現在的問題是無窮遠在射影空間中純粹是一種數學構造,不一定代表著現實世界中的無窮遠,但目前的量子場論告訴我們理想世界的無窮遠可能真的也是現實世界中的無窮遠,由於量子場論已經在很大的精度上被證實了,可以得到的結論是即使理想世界的無窮遠並不意謂著現實世界中的無窮遠,至少在目前觀測範圍內它們是大致相同的。
但現在還是有了新的物理。首先,時空在射影空間中擁有最大的對稱性,需要最多的參數描述,而映射回仿射空間或閔可夫斯基空間後,參數自然會減少,用量子場論的話說就是對稱性自發破缺了,可見如果我們沿用量子場論的對稱性自發破缺一詞純屬誤稱,因為量子細胞場論中的這種破缺不需要一種背景場,不過量子場論中屬於誤稱的名詞還有很多,這也反映了量子場論的先輩們在探求真理的道路上走的是一條充滿坎坷的路;另外,點線對偶性給出的自旋為0的粒子的對稱性是動態的,現在Higgs機制需要的兩個要素我們都有了,所以量子細胞場論與Higgs機制也是兼容的,只是不需要Higgs背景場。
其次,量子電動力學中的截斷被作為一種重正化的輔助參數引入,截斷動量是隨意引入的,至於截斷動量數值的大小是沒有實際物理意義的;量子色動力學中的重正化群理論部分地改變了這種看法,截斷動量雖然沒有絕對的物理意義,卻可能有相對的物理意義,例如引出漸近自由的概念等等;量子細胞場論進一步改變了這種看法,原因在於理想世界中的無窮遠點不一定是現實世界中的無窮遠點,例如假設理想世界的無窮遠點對應的不是現實世界的無窮遠點而是截斷動量的話,那麽截斷動量之上的物質就很可能是宇宙中的暗物質,這樣我們就可以為暗能量和暗物質都給出一個解釋;另外,低頻截斷對應的很可能是色禁閉效應;關於這方面我們將做進一步的探討。眼下,將量子場論的重正化翻譯成量子細胞場論中的無窮遠的語言是有趣也是有意義的工作;例如我們可以證明量子場論確實是自洽的,從而解決這一困擾物理學界半個多世紀的難題,我個人認為憑這一成果獲得諾貝爾物理學獎或者沃夫物理學獎也是應該的;Joking?
如果把時空的無窮遠點看成是一個點,那麽任何一個局域規範變換都可分解成一個整體規範變換和一個在無窮遠點等於1的局部規範變換。局部變換下的不變性可以歸結為格林函數的生成泛函要滿足一個恒等式,通常稱為Slavnov-Taylor恒等式,或稱為廣義的Ward-Takahashi恒等式;從Slavnov-Taylor恒等式可以推導出Green函數或頂角函數所滿足的一系列關系。Slavnov-Taylor恒等式要比Ward-Takahashi恒等式更普遍,前者為頂角函數生成泛函所滿足的一個泛函微商恒等式,後者是三點和兩點頂角所滿足的恒等式,並可從前者推導出來。
從這個模型出發可以導出很多有意義的結論,利用我們鐵環與路面的類比,我們知道在電磁場中位置和動量確實是對偶的場量;回想電磁場量子化的歷史,簡單地將電磁場量子化,人們發現與庫侖勢共軛的動量恒為零,於是才有了Gupta-Bleuler利用不定度規的量子化方法,細胞量子化方法與Gupta-Bleuler方法等價,並且提供了一個Gupta-Bleuler量子化方法的直觀的幾何模型。之所以選擇龐加萊模型是與射影空間的特定性質有關系的,當我們將射影空間改造成度量空間後,移動了多少距離和轉過了多少角度完全是對偶的概念;以引力為例,在de Sitter時空中即宇宙邊界上的移動與在內部的反de Sitter時空中轉過多少角度是對偶的。所以在量子細胞場論中,代表旋轉的自旋為1的矢量分量與代表移動的自旋為0的標量分量完全是對偶的不可能分割的整體;而在傳統量子場論中,這兩種分量是分開來處理的。
費曼稱量子電動力學中的無窮大是腦筋不正常的,從現實的角度出發我們也知道帶著量子場論中沒有物理意義的無窮大試圖構建統一場論也是一件不可能完成的任務。既然在量子細胞場論中,位置與動量是一對共軛的場量,而無窮遠點是位置的極限,無窮大是量子電動力學中動量的極限,可見最子細胞場論中的無窮遠與量子場論中的無窮大之間確實存在對偶關系;量子場論牽涉到無窮大的加減乘除運算,就目前人類已經掌握的數學知識體系而言,只有射影空間中的無窮遠是可以直接實施加減乘除運算的從而獲得邏輯上自洽的結果,所以從量子場論發展到量子細胞場論在邏輯上的必然的,所謂自古華山一條路,人類還沒有找到其它處理無窮的辦法。
從量子場論發展到量子細胞場論,腦筋終於正常了!以下為了討論的方便,我們將量子細胞場論中的愛因斯坦空間簡稱為理想世界,將量子場論中以閔可夫斯基空間為基底的物理世界稱為現實世界;現在的問題是無窮遠在射影空間中純粹是一種數學構造,不一定代表著現實世界中的無窮遠,但目前的量子場論告訴我們理想世界的無窮遠可能真的也是現實世界中的無窮遠,由於量子場論已經在很大的精度上被證實了,可以得到的結論是即使理想世界的無窮遠並不意謂著現實世界中的無窮遠,至少在目前觀測範圍內它們是大致相同的。
但現在還是有了新的物理。首先,時空在射影空間中擁有最大的對稱性,需要最多的參數描述,而映射回仿射空間或閔可夫斯基空間後,參數自然會減少,用量子場論的話說就是對稱性自發破缺了,可見如果我們沿用量子場論的對稱性自發破缺一詞純屬誤稱,因為量子細胞場論中的這種破缺不需要一種背景場,不過量子場論中屬於誤稱的名詞還有很多,這也反映了量子場論的先輩們在探求真理的道路上走的是一條充滿坎坷的路;另外,點線對偶性給出的自旋為0的粒子的對稱性是動態的,現在Higgs機制需要的兩個要素我們都有了,所以量子細胞場論與Higgs機制也是兼容的,只是不需要Higgs背景場。
其次,量子電動力學中的截斷被作為一種重正化的輔助參數引入,截斷動量是隨意引入的,至於截斷動量數值的大小是沒有實際物理意義的;量子色動力學中的重正化群理論部分地改變了這種看法,截斷動量雖然沒有絕對的物理意義,卻可能有相對的物理意義,例如引出漸近自由的概念等等;量子細胞場論進一步改變了這種看法,原因在於理想世界中的無窮遠點不一定是現實世界中的無窮遠點,例如假設理想世界的無窮遠點對應的不是現實世界的無窮遠點而是截斷動量的話,那麽截斷動量之上的物質就很可能是宇宙中的暗物質,這樣我們就可以為暗能量和暗物質都給出一個解釋;另外,低頻截斷對應的很可能是色禁閉效應;關於這方面我們將做進一步的探討。眼下,將量子場論的重正化翻譯成量子細胞場論中的無窮遠的語言是有趣也是有意義的工作;例如我們可以證明量子場論確實是自洽的,從而解決這一困擾物理學界半個多世紀的難題,我個人認為憑這一成果獲得諾貝爾物理學獎或者沃夫物理學獎也是應該的;Joking?
如果把時空的無窮遠點看成是一個點,那麽任何一個局域規範變換都可分解成一個整體規範變換和一個在無窮遠點等於1的局部規範變換。局部變換下的不變性可以歸結為格林函數的生成泛函要滿足一個恒等式,通常稱為Slavnov-Taylor恒等式,或稱為廣義的Ward-Takahashi恒等式;從Slavnov-Taylor恒等式可以推導出Green函數或頂角函數所滿足的一系列關系。Slavnov-Taylor恒等式要比Ward-Takahashi恒等式更普遍,前者為頂角函數生成泛函所滿足的一個泛函微商恒等式,後者是三點和兩點頂角所滿足的恒等式,並可從前者推導出來。
等積仿射變換,又稱為幺模仿射變換
可以證明,只要從兩個坐標系x、y、z、t和x'、y'、z'、t'中的一個光速的等式,就可以知道從坐標x、y、z、t到坐標x'、y'、z'、t'的變換公式是線性的和齊次的;另外這個變換的行列式等於1。如果x、y、z、t滿足光速的方程,則它們經過變換而得到的x'、y'、z'、t'也滿足光速方程;這種變換叫做洛侖茲變換。
我們先來討論當點沿著Ox軸運動的最簡單的情形,為了方便起見我們令光速c=1。我們把x和t看做平面上的直角坐標,即我們從幾何上來考慮問題,並且我們認為洛侖茲變換L是平面Oxt的仿射變換的公式;則這個變換把一對相交的直線x±t=0變成自己。因此,變換L是沿著這兩條直線作具有相同系數的壓縮和伸展的聯合。我們再討論當點在平面Oxy上運動的情形,光速公式是在平面Oxy上的運動的洛侖茲公式。我們把x、y、t看做普通三維空間中點的笛卡兒直角坐標,並且把洛侖茲變換看做這個空間的仿射變換的公式;則光速公式表示一個頂角是90度的正圓錐K。從洛侖茲變換的這個幾何解釋看來,平面上的運動不是別的,正是這個空間的把錐面K變成自己的所有不改變體積的等積仿射變換。
我們看到,洛侖茲變換的理論、射影幾何和透視理論,以及歐幾裏德幾何,都彼此有著緊密的聯系;與它們在很多方面有聯系的還有復變函數論裏所謂的保角變換。眾所周知,在歐氏幾何中,面積是用距離定義的,這種定義不能直接應用到仿射幾何中來,這是因為距離這個概念在仿射幾何裏是沒有定義的,但是,在數學分析中,面積是用積分定義的,積分的定義與直角坐標x、y有關,是依賴於長度和垂直等概念的,當然也不能直接應用於仿射幾何之中,然而值得註意的是積分∫∫F(x,y)dxdy的嚴格定義是純解析的,完全不依賴於直角坐標x和y,而且運算規律和通常一致。如果D是仿射平面Oxt的一個區域,那麽在一般的仿射變換下D的面積不是不變的,可是對於Jacobi行列式Δ=±1的那些仿射變換,面積卻是不變的,稱為幺模仿射變換或等積仿射變換,幺模仿射變換的全體構成一個群,這個群和它所對應的幾何都是幺模仿射的,不難證明幺模仿射變換下的面積元是一種特殊的外微分形式。
讓我們來討論某些這種特殊的洛侖茲變換。1、明顯地,空間作為剛體繞錐面K的軸轉一個角ω的任何簡單的旋轉,是空間的把錐面K變成自己的等積仿射變換,即是一些特殊的洛侖茲變換。2、空間對通過錐面K的軸的任何平面的反射π,顯然也是這種洛侖茲變換。3、最後,讓我們看一下以下的變換;設v和w是錐面K的某一對對面的母線,P和Q是沿這兩條母線與錐面相切的平面;這兩個平面互相垂直。我們作空間向著平面P的壓縮和它背著平面Q而具有同一個系數的伸展,或者反之。例如我們把空間向著平面P壓縮到三分之一,然後背著平面Q把它伸展到三倍。這種空間變換L顯然是仿射變換而且是保留所有體積的大小的;這個變換把錐面K變成自己。由於錐面以t軸作為旋轉軸,總可以把整個圖形旋轉到使母線v和w處在例如平面Sxt上。
我們使平行於平面Sxt的任意平面R與錐面K相交;這個平面有方程y=b,這裏b是常數。把這個值代入錐面K的方程,可以得到一個雙曲線的方程,對於它說,平面R與平面P和Q的交線正是漸近線;刻劃這個雙曲線的點是:它到漸近線,即到平面P和Q的距離p和q的乘積是常數,在變換L下,這種雙曲線上的每一個點都留在同一條雙曲線上,因而雙曲線就變成了自己,但是整個錐面K就由這種雙曲線組成,所以在空間變換L下錐面K變成了自己;因此這個變換L也是洛侖茲變換。
因為在仿射變換下直線變成直線,而且相交直線變成相交直線,所以直線叢S在任何洛侖茲變換下一對一的變成自己;此外,因為在空間的仿射變換下每一個平面都變成一個平面,所以在叢S到自己的這種變換下得到的是這個叢的射影變換,如果用一個垂直於錐面K的軸的平面Π與這個叢相交,而且認為這個平面完全不參與空間的所說洛侖茲變換,再把這個平面增補為射影平面Π*,來考慮叢S的直線與平面Π*的交點,則變換叢S的洛侖茲變換,順帶給出平面Π*的一個射影變換Λ,它把由平面Π*與錐面K的內部相交而成的圓形α變成自己。為了研究洛侖茲變換的性質,最簡單的是考慮它的所謂把圓α變成自己的射影變換Λ。
我們先來討論當點沿著Ox軸運動的最簡單的情形,為了方便起見我們令光速c=1。我們把x和t看做平面上的直角坐標,即我們從幾何上來考慮問題,並且我們認為洛侖茲變換L是平面Oxt的仿射變換的公式;則這個變換把一對相交的直線x±t=0變成自己。因此,變換L是沿著這兩條直線作具有相同系數的壓縮和伸展的聯合。我們再討論當點在平面Oxy上運動的情形,光速公式是在平面Oxy上的運動的洛侖茲公式。我們把x、y、t看做普通三維空間中點的笛卡兒直角坐標,並且把洛侖茲變換看做這個空間的仿射變換的公式;則光速公式表示一個頂角是90度的正圓錐K。從洛侖茲變換的這個幾何解釋看來,平面上的運動不是別的,正是這個空間的把錐面K變成自己的所有不改變體積的等積仿射變換。
我們看到,洛侖茲變換的理論、射影幾何和透視理論,以及歐幾裏德幾何,都彼此有著緊密的聯系;與它們在很多方面有聯系的還有復變函數論裏所謂的保角變換。眾所周知,在歐氏幾何中,面積是用距離定義的,這種定義不能直接應用到仿射幾何中來,這是因為距離這個概念在仿射幾何裏是沒有定義的,但是,在數學分析中,面積是用積分定義的,積分的定義與直角坐標x、y有關,是依賴於長度和垂直等概念的,當然也不能直接應用於仿射幾何之中,然而值得註意的是積分∫∫F(x,y)dxdy的嚴格定義是純解析的,完全不依賴於直角坐標x和y,而且運算規律和通常一致。如果D是仿射平面Oxt的一個區域,那麽在一般的仿射變換下D的面積不是不變的,可是對於Jacobi行列式Δ=±1的那些仿射變換,面積卻是不變的,稱為幺模仿射變換或等積仿射變換,幺模仿射變換的全體構成一個群,這個群和它所對應的幾何都是幺模仿射的,不難證明幺模仿射變換下的面積元是一種特殊的外微分形式。
讓我們來討論某些這種特殊的洛侖茲變換。1、明顯地,空間作為剛體繞錐面K的軸轉一個角ω的任何簡單的旋轉,是空間的把錐面K變成自己的等積仿射變換,即是一些特殊的洛侖茲變換。2、空間對通過錐面K的軸的任何平面的反射π,顯然也是這種洛侖茲變換。3、最後,讓我們看一下以下的變換;設v和w是錐面K的某一對對面的母線,P和Q是沿這兩條母線與錐面相切的平面;這兩個平面互相垂直。我們作空間向著平面P的壓縮和它背著平面Q而具有同一個系數的伸展,或者反之。例如我們把空間向著平面P壓縮到三分之一,然後背著平面Q把它伸展到三倍。這種空間變換L顯然是仿射變換而且是保留所有體積的大小的;這個變換把錐面K變成自己。由於錐面以t軸作為旋轉軸,總可以把整個圖形旋轉到使母線v和w處在例如平面Sxt上。
我們使平行於平面Sxt的任意平面R與錐面K相交;這個平面有方程y=b,這裏b是常數。把這個值代入錐面K的方程,可以得到一個雙曲線的方程,對於它說,平面R與平面P和Q的交線正是漸近線;刻劃這個雙曲線的點是:它到漸近線,即到平面P和Q的距離p和q的乘積是常數,在變換L下,這種雙曲線上的每一個點都留在同一條雙曲線上,因而雙曲線就變成了自己,但是整個錐面K就由這種雙曲線組成,所以在空間變換L下錐面K變成了自己;因此這個變換L也是洛侖茲變換。
因為在仿射變換下直線變成直線,而且相交直線變成相交直線,所以直線叢S在任何洛侖茲變換下一對一的變成自己;此外,因為在空間的仿射變換下每一個平面都變成一個平面,所以在叢S到自己的這種變換下得到的是這個叢的射影變換,如果用一個垂直於錐面K的軸的平面Π與這個叢相交,而且認為這個平面完全不參與空間的所說洛侖茲變換,再把這個平面增補為射影平面Π*,來考慮叢S的直線與平面Π*的交點,則變換叢S的洛侖茲變換,順帶給出平面Π*的一個射影變換Λ,它把由平面Π*與錐面K的內部相交而成的圓形α變成自己。為了研究洛侖茲變換的性質,最簡單的是考慮它的所謂把圓α變成自己的射影變換Λ。
量子細胞引力論
由於量子細胞引力耦合常數是無量綱的,就為重正化鋪平了道路。我們現在已經知道了引力子的構造,由點線對偶性生成一個自旋為1的規範玻色子,這差不多就是普通的光子;由伸縮對偶性生成一個自旋為1的需要重整化的規範玻色子,引力子是由這兩個自旋為1的規範玻色子合成出來的自旋為2的玻色子。所以傳遞作用力的規範玻色子都是由普通的光子加上一些佐料構成的,至少在量子細胞場論中是如此。可以看出,量子場論中那些“腦筋不正常的過程”正是量子細胞引力論的起點,不過到了射影空間變得“腦筋正常”了而已。沿著量子場論的思路就可以證明量子細胞引力論是局部可重正化的。
我們將自旋為0的引力子稱為牛頓引力子,自旋為2的引力子稱為愛因斯坦引力子;下圖是引力子的樣子:
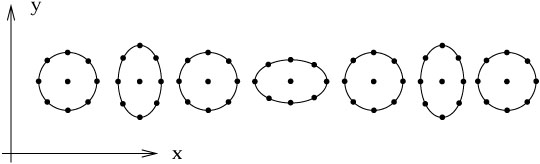
從量子場論和廣義相對論的幾個方面都會導致引力常數無量綱的結果;沿著Dirac的思路,當Dirac嘗試推導相對論量子力學時采用虛擬開根號的方法,微分算符的一階條件導致Dirac算子是能量算符的平方根;另外引力場的Hilbert作用量中包含度規行列式的平方根算符,直接對這個平方根算符展開會在作用量基本方程中得到一個引力子的無窮展開級數,這相當於一個無限的引力子自作用序列,而量子色動力學的Yang-Mills場的基本方程中關於膠子的展開級數除了包含三膠子自作用和四膠子自作用頂點外不包含更高階的膠子自作用頂點。
這樣就將質量有關項吸收進了質量荷中,相當於在引力作用量基本方程引入了一個截斷,現在引力子的自作用也只包含三引力子頂點或四引力子自作用頂點而不包含更高的自作用項;另外,我們知道正交標架場相當於度規算符的平方根,所以引力耦合常數無量綱其實有幾個方面的意義,現在引力場和Yang-Mills場有了完全一樣的場方程式。對於宇宙而言,有質量物質和引力子都被封閉在一個馬德西特袋中,量子細胞引力場有漸近自由的性質;這很像量子色動力學中誇克和膠子都被封閉在重子口袋裏,所以有漸近自由的性質;所以可以得出結論,雙重橢圓幾何加雙曲幾何可以得到漸近自由的性質;問題是黑洞遵守的是單重橢圓幾何性質,畢竟重子不會胡亂地發射膠子,而黑洞可以發射引力子,如果黑洞中的引力也有漸近自由性質,則自然可以避免奇點的產生,但如果黑洞中的引力沒有漸近自由的性質,就要想別的辦法避免奇點的產生了。
當然我們不能對耦合常數無量綱太迷信,現代物理實驗證實所謂跑動耦合常數其實是與能標有關系的,我想無量綱耦合常數最大的好處是我們能將大自然四種基本力的場方程用一個極其簡單的統一拉格朗日量寫出來,即自由拉格朗日量加上一個耦合拉格朗日項;而且我們發現了大自然的另一處自相似性,即宇宙和核子之間存在著相似性,這樣我們就以非常直觀的方式給出了漸近自由的一個解釋,而不需要一大堆繁雜的數學。
考慮兩個有質量粒子通過交換引力子產生引力,沿著有質量粒子作一個無窮小的圓,根據復變函數的留數定理沿著圓積分會給出一個不變量,同時,兩個有質量粒子的無窮小圓相交於兩個無窮遠的虛圓點,連接兩個虛圓點有一條無窮遠的公共弦,我們認出這兩個虛圓點有點類似於產生電磁力的正電荷與負電荷;也許引力與電磁力還有更深層次上的對偶關系,不過我們現在不想深究這種類馬德西納似的關系;重要的是,正的引力電荷與負的引力電荷會使兩個有質量粒子產生極化,兩個有質量粒子變得像是電磁場中的偶極子,於是引力便產生了;但引力偶極子與電磁偶極子有一個重要差別,引力偶極子不會產生偶極輻射,考慮邁克爾喬丹飛身躍起扣籃,地球會向相反的方向運動從而抵消這種衝量,所以引力只會引進四極輻射;產生這種現象的微觀原因是:局部的引力保持一對對合點不變,屬於單重橢圓幾何,需要將對徑點等同起來認為是同一點,所以引力波在轉過了180度後波函數保持不變。
虛的正負引力電荷產生的場是對稱的,怎麽會產生一個馬德西特式的宇宙呢,原因主要有兩個方面:一是這種對稱性是非常不穩定的,像是立在桌子上的一支筷子,總要倒下來導致對稱性破缺;二是按照現代宇宙論的觀點宇宙一定是一個沒有邊界的四維流形,自然是封閉的,所以也自然會產生引力的一個取向。引力場有很強的整體效應,會產生一個整體的背景場,但這種背景場不是量子場論中那種從虛無的真空中產生出的背景場;所以牛頓引力子實際上包含兩種成份:一種是導致牛頓引力勢的自旋為0的分量,一種是由於量子場論中所謂的真空自發性破缺產生的一個Goldstone玻色子;但要記住,量子細胞場論中沒有一個所謂無窮大的真空態。
我們將自旋為0的引力子稱為牛頓引力子,自旋為2的引力子稱為愛因斯坦引力子;下圖是引力子的樣子:

從量子場論和廣義相對論的幾個方面都會導致引力常數無量綱的結果;沿著Dirac的思路,當Dirac嘗試推導相對論量子力學時采用虛擬開根號的方法,微分算符的一階條件導致Dirac算子是能量算符的平方根;另外引力場的Hilbert作用量中包含度規行列式的平方根算符,直接對這個平方根算符展開會在作用量基本方程中得到一個引力子的無窮展開級數,這相當於一個無限的引力子自作用序列,而量子色動力學的Yang-Mills場的基本方程中關於膠子的展開級數除了包含三膠子自作用和四膠子自作用頂點外不包含更高階的膠子自作用頂點。
這樣就將質量有關項吸收進了質量荷中,相當於在引力作用量基本方程引入了一個截斷,現在引力子的自作用也只包含三引力子頂點或四引力子自作用頂點而不包含更高的自作用項;另外,我們知道正交標架場相當於度規算符的平方根,所以引力耦合常數無量綱其實有幾個方面的意義,現在引力場和Yang-Mills場有了完全一樣的場方程式。對於宇宙而言,有質量物質和引力子都被封閉在一個馬德西特袋中,量子細胞引力場有漸近自由的性質;這很像量子色動力學中誇克和膠子都被封閉在重子口袋裏,所以有漸近自由的性質;所以可以得出結論,雙重橢圓幾何加雙曲幾何可以得到漸近自由的性質;問題是黑洞遵守的是單重橢圓幾何性質,畢竟重子不會胡亂地發射膠子,而黑洞可以發射引力子,如果黑洞中的引力也有漸近自由性質,則自然可以避免奇點的產生,但如果黑洞中的引力沒有漸近自由的性質,就要想別的辦法避免奇點的產生了。
當然我們不能對耦合常數無量綱太迷信,現代物理實驗證實所謂跑動耦合常數其實是與能標有關系的,我想無量綱耦合常數最大的好處是我們能將大自然四種基本力的場方程用一個極其簡單的統一拉格朗日量寫出來,即自由拉格朗日量加上一個耦合拉格朗日項;而且我們發現了大自然的另一處自相似性,即宇宙和核子之間存在著相似性,這樣我們就以非常直觀的方式給出了漸近自由的一個解釋,而不需要一大堆繁雜的數學。
考慮兩個有質量粒子通過交換引力子產生引力,沿著有質量粒子作一個無窮小的圓,根據復變函數的留數定理沿著圓積分會給出一個不變量,同時,兩個有質量粒子的無窮小圓相交於兩個無窮遠的虛圓點,連接兩個虛圓點有一條無窮遠的公共弦,我們認出這兩個虛圓點有點類似於產生電磁力的正電荷與負電荷;也許引力與電磁力還有更深層次上的對偶關系,不過我們現在不想深究這種類馬德西納似的關系;重要的是,正的引力電荷與負的引力電荷會使兩個有質量粒子產生極化,兩個有質量粒子變得像是電磁場中的偶極子,於是引力便產生了;但引力偶極子與電磁偶極子有一個重要差別,引力偶極子不會產生偶極輻射,考慮邁克爾喬丹飛身躍起扣籃,地球會向相反的方向運動從而抵消這種衝量,所以引力只會引進四極輻射;產生這種現象的微觀原因是:局部的引力保持一對對合點不變,屬於單重橢圓幾何,需要將對徑點等同起來認為是同一點,所以引力波在轉過了180度後波函數保持不變。
虛的正負引力電荷產生的場是對稱的,怎麽會產生一個馬德西特式的宇宙呢,原因主要有兩個方面:一是這種對稱性是非常不穩定的,像是立在桌子上的一支筷子,總要倒下來導致對稱性破缺;二是按照現代宇宙論的觀點宇宙一定是一個沒有邊界的四維流形,自然是封閉的,所以也自然會產生引力的一個取向。引力場有很強的整體效應,會產生一個整體的背景場,但這種背景場不是量子場論中那種從虛無的真空中產生出的背景場;所以牛頓引力子實際上包含兩種成份:一種是導致牛頓引力勢的自旋為0的分量,一種是由於量子場論中所謂的真空自發性破缺產生的一個Goldstone玻色子;但要記住,量子細胞場論中沒有一個所謂無窮大的真空態。
相對論的絕對時空觀
1908年9月,赫爾曼.閔可夫斯基通過與畢達哥拉斯公式的類比,發現了他的絕對時空。你可能記得,閔可夫斯基就是在愛因斯坦讀書時叫他懶狗的那位數學教授。1902年,俄國出身的閔可夫斯基離開了愛因斯坦的母校蘇黎世ETH,到享有國際聲譽的德國哥廷根任教。在哥廷根,閔可夫斯基研究了愛因斯坦關於狹義相對論的論文,印象很深,這引導他發現了四維時空的絕對性質。
愛因斯坦聽說閔可夫斯基的發現時,並不在意。閔可夫斯基只是用一種新的更數學化的語言重寫了狹義相對論的定律,而對於愛因斯坦來說,數學掩蓋了定律背後的物理意義。因為閔可夫斯基不斷宣揚他的絕對時空觀如何美妙,愛因斯坦開始笑話哥廷根的數學家。事實上,笑話落到了愛因斯坦自己身上。在4年後的1912年,為了在狹義相對論中納入引力,愛因斯坦妥協了,閔可夫斯基的絕對時空觀成了廣義相對論的根本基礎;遺憾的是,閔可夫斯基沒能活著看到這一點,1909年,他死於闌尾炎,終年45歲。
愛因斯坦的數學功底顯然不如Hilbert,愛因斯坦不是第一個發現卷曲定律的正確形式的人,第一個發現者是Hilbert;1915年,Hilbert沒有走愛因斯坦那條艱難的試錯路線,而是走的一條優美而簡捷的看似“神學”的數學道路,推導出Einstein-Hilbert作用量,比愛因斯坦在柏林向普魯士科學院報告相同定律早5天。愛因斯坦用的是張量分析,用陳省身的話說,從現代微分幾何的觀點來看,張量分析弊多利少,但張量分析簡單明了,在初等問題上的功用是不可磨滅的。不幸的是,量子場論的基礎也是閔可夫斯基的絕對時空觀,可能雖然Klein很支持愛因斯坦,但愛因斯坦對klein的愛爾朗根綱領並不熟悉,所以沒有找到相對時空觀的正確表述形式,所以從量子場論和廣義相對論的絕對時空觀過渡到量子細胞場論的相對時空觀,不僅在邏輯上而且在歷史上都是必然的。當然我們用龐加萊模型和Klein的愛爾朗根綱領來統一規範場和引力場隱含了一個假設,即引力場是最大對稱化的,由於目前所有關於引力的驗證事實都隱含了最大對稱化條件,所以這種假設也是合理的;用廣義相對論的話說,量子細胞引力論與廣義相對論在弱等效原理下是等價的,但廣義相對論的強等效原理並未經過實驗證實。
愛因斯坦聽說閔可夫斯基的發現時,並不在意。閔可夫斯基只是用一種新的更數學化的語言重寫了狹義相對論的定律,而對於愛因斯坦來說,數學掩蓋了定律背後的物理意義。因為閔可夫斯基不斷宣揚他的絕對時空觀如何美妙,愛因斯坦開始笑話哥廷根的數學家。事實上,笑話落到了愛因斯坦自己身上。在4年後的1912年,為了在狹義相對論中納入引力,愛因斯坦妥協了,閔可夫斯基的絕對時空觀成了廣義相對論的根本基礎;遺憾的是,閔可夫斯基沒能活著看到這一點,1909年,他死於闌尾炎,終年45歲。
愛因斯坦的數學功底顯然不如Hilbert,愛因斯坦不是第一個發現卷曲定律的正確形式的人,第一個發現者是Hilbert;1915年,Hilbert沒有走愛因斯坦那條艱難的試錯路線,而是走的一條優美而簡捷的看似“神學”的數學道路,推導出Einstein-Hilbert作用量,比愛因斯坦在柏林向普魯士科學院報告相同定律早5天。愛因斯坦用的是張量分析,用陳省身的話說,從現代微分幾何的觀點來看,張量分析弊多利少,但張量分析簡單明了,在初等問題上的功用是不可磨滅的。不幸的是,量子場論的基礎也是閔可夫斯基的絕對時空觀,可能雖然Klein很支持愛因斯坦,但愛因斯坦對klein的愛爾朗根綱領並不熟悉,所以沒有找到相對時空觀的正確表述形式,所以從量子場論和廣義相對論的絕對時空觀過渡到量子細胞場論的相對時空觀,不僅在邏輯上而且在歷史上都是必然的。當然我們用龐加萊模型和Klein的愛爾朗根綱領來統一規範場和引力場隱含了一個假設,即引力場是最大對稱化的,由於目前所有關於引力的驗證事實都隱含了最大對稱化條件,所以這種假設也是合理的;用廣義相對論的話說,量子細胞引力論與廣義相對論在弱等效原理下是等價的,但廣義相對論的強等效原理並未經過實驗證實。
終於統一了?
有了前面這些基礎知識的鋪墊,我們現在可以將四種基本力統一起來考慮了。關於誇克禁閉這在量子細胞場論中有個超級簡單的解釋,由於強力屬於多細胞生物,所以單獨的細胞也就是誇克不能構成生命,當然我們不能將這種解釋看得太認真,我們需要嚴格的邏輯推理,否則本文應該改稱“大話統一場論”了;況且除了誇克禁閉外,量子細胞場論還要解決大量的其它實際問題。維爾茨克說今天量子色動力學理論在原子核實際問題中的角色,基本上同“聖水”差不多,哈羅德•弗裏茨寫道:“諷刺的是,QCD理論沒有提供多少有關強相互作用的內容,而這正是我們研究的最初動機。”下面我們會看到,量子細胞場論大大改善了量子場論在核子相互作用中的看法。
化學鍵能為我們提供一些線索。氖是一種惰性氣體,每個原子都是一個不發生相互作用、不帶電荷的近乎完美的球體,但當兩個原子相互靠近的時候,每個原子所帶的電子雲相對於原子核都發生了微小的偏移,結果每個原子都會呈現一點兒電極性,因此距離很近的兩個原子之間存在吸引力,這就是範德瓦爾斯力。
量子細胞場論確實能為我們提供理解原子核力的基礎。引力與強力都是多細胞的量子生命形式,所以兩者之間有很多相似性;可以設想,誇克生存在一個正曲率的緊致無邊的四維流形中,這正是黎曼幾何的基本假設,所以我們這樣假設也是合理的,重要的是,這個無邊的四維緊致流形構成了膠子世界的邊界;要記住膠子都是些虛粒子,它們的能量是借來的,既然是借來的就一定要還的,所以膠子的測地線自然終止於誇克;膠子生存在一個龐加萊雙曲幾何空間裏,膠子是嚴格無質量的,所以即使龐加萊雙曲幾何的邊界為無窮遠,膠子還是能夠到達邊界的。我們看到,重子確實是一種口袋的形狀,這是誇克禁閉的第一條線索。
同引力場一樣,誇克場服從單重橢圓幾何定律,而核子本身卻是一個服從雙重橢圓幾何模型的客體,雖然我們沒有黑洞與宇宙滿足對偶性的證據,強力場卻明顯地滿足單重橢圓幾何與雙重橢圓幾何的對偶性,這已經被大量的高能加速器實驗所證實。主要原因是核子的自旋是1/2,在量子細胞場論中,自旋為1/2就意謂著一定有一對對偶的場在相互轉化;由於在量子細胞場論中標量粒子與矢量粒子是對偶的,所以我們只考慮標量粒子,在量子細胞場論中有兩種標量粒子:一種是攜帶色力勢的標量粒子,我們稱之為色庫侖子,一種是傳說中的Goldstone玻色子;但量子細胞場論中沒有真空自發性破缺之說,所謂Goldstone玻色子也是狹義相對論本身導出的,所以聲子也與量子場論的聲子有很大的不同;我們必須為量子細胞場論中的聲子起一個新的名字,比如說哼哈子(Henghaon),當然我們推薦的名稱是行者或者輸運子(Travellon);之所以起這樣的名字是因為它們在量子色動力學中的表兄弟瞬子可以起到在不同維空間的量子隧道中穿越的作用。
行者雖然不是真空自發性破缺所產生的,但與凝聚卻有關系,負責將能量輸送到雙重橢圓幾何的對徑點上;就好像我們從地球的北極運送物質到地球的南極,北極與南極之間的測地線不存在,但我們可以選任何一條路徑,但量子力學就不同了,由於沒有測地線,行者一定是經過所有的路徑到達對徑點;這樣就會與所有的誇克發生相互作用。由於存在這種單重橢圓幾何與雙重橢圓幾何的對偶關系,所以核力的同位旋對稱性實際上是這種對偶關系引起的相互作用,用量子色動力學的話說,是色力的剩余相互作用。
不管是色庫侖子還是行者都起著將對徑點疊合起來的作用,只是前者是對合關系,後者是輸運關系,這就要求介子一定是由一個正誇克和一個反誇克組成的無色的粒子。關於誇克禁閉還有一種更強的約束,我們知道重子是由三個誇克組成的,蓋爾曼先生很可能是童話小說看多了,叫了三聲誇克,便虛構出了誇克這種數學對象,但誇克很可能並不對應於任何真實的物理粒子,就好像費曼的鬼粒子並不對應真實的物理粒子一樣。射影空間中有一種自配極三角形,由於是自配極的,所以也滿足點線對偶性,從而與行者是兼容的;重要的是,自配級三角形的面積在幺模仿射變換下是一個不變量,所以是與狹義相對論兼容的;更重要的是,假設誇克位於自配極三角形的三個頂點上,自配極三角形的面積解釋為荷的話,荷是一個整數,不會出現每個誇克帶1/3電荷這種奇怪的事,所以也沒有自由誇克的說法。量子場論通過高能加速器擊碎原子試圖發現自由誇克的方法,這種試驗方法是值得推崇的,但量子場論的邏輯推理是有問題的;這就好像將一輛汽車經過粉碎機粉碎成無數塊慘不忍睹的碎片,然後每個碎片又會自動還原成一輛完整的汽車;一句話,QCD是還原論的,量子細胞場論是整體論的。
其實我們一直都小心翼翼的,避免與量子場論有太多矛盾的地方,我們還是有了一個容納了大自然四種基本力的統一的幾何模型,與量子場論的兼容性很好,而且比量子場論更簡單也更能貼近實驗事實;量子細胞場論沒有困擾量子場論的所謂強CP破缺問題,沒有軸矢量流的三角形反常問題。由規範勢導出的標量粒子滿足單重橢圓幾何,與矢量粒子合在一起後就變成了極矢量;行者是動態的並且滿足雙重橢圓幾何,與矢量粒子合在一起後就變成了軸矢量。當我們要求將對徑點疊合後,電弱力的兩個對合點上分別是電子和中微子,所以對於弱相互作用宇稱是不守恒的;核力的兩個對合點上分別是中子和質子,我們看到,強力中所謂的軸矢量流部分守恒在量子細胞場論中是這樣解釋的,強力並不破壞宇稱的手征對稱性。
化學鍵能為我們提供一些線索。氖是一種惰性氣體,每個原子都是一個不發生相互作用、不帶電荷的近乎完美的球體,但當兩個原子相互靠近的時候,每個原子所帶的電子雲相對於原子核都發生了微小的偏移,結果每個原子都會呈現一點兒電極性,因此距離很近的兩個原子之間存在吸引力,這就是範德瓦爾斯力。
量子細胞場論確實能為我們提供理解原子核力的基礎。引力與強力都是多細胞的量子生命形式,所以兩者之間有很多相似性;可以設想,誇克生存在一個正曲率的緊致無邊的四維流形中,這正是黎曼幾何的基本假設,所以我們這樣假設也是合理的,重要的是,這個無邊的四維緊致流形構成了膠子世界的邊界;要記住膠子都是些虛粒子,它們的能量是借來的,既然是借來的就一定要還的,所以膠子的測地線自然終止於誇克;膠子生存在一個龐加萊雙曲幾何空間裏,膠子是嚴格無質量的,所以即使龐加萊雙曲幾何的邊界為無窮遠,膠子還是能夠到達邊界的。我們看到,重子確實是一種口袋的形狀,這是誇克禁閉的第一條線索。
同引力場一樣,誇克場服從單重橢圓幾何定律,而核子本身卻是一個服從雙重橢圓幾何模型的客體,雖然我們沒有黑洞與宇宙滿足對偶性的證據,強力場卻明顯地滿足單重橢圓幾何與雙重橢圓幾何的對偶性,這已經被大量的高能加速器實驗所證實。主要原因是核子的自旋是1/2,在量子細胞場論中,自旋為1/2就意謂著一定有一對對偶的場在相互轉化;由於在量子細胞場論中標量粒子與矢量粒子是對偶的,所以我們只考慮標量粒子,在量子細胞場論中有兩種標量粒子:一種是攜帶色力勢的標量粒子,我們稱之為色庫侖子,一種是傳說中的Goldstone玻色子;但量子細胞場論中沒有真空自發性破缺之說,所謂Goldstone玻色子也是狹義相對論本身導出的,所以聲子也與量子場論的聲子有很大的不同;我們必須為量子細胞場論中的聲子起一個新的名字,比如說哼哈子(Henghaon),當然我們推薦的名稱是行者或者輸運子(Travellon);之所以起這樣的名字是因為它們在量子色動力學中的表兄弟瞬子可以起到在不同維空間的量子隧道中穿越的作用。
行者雖然不是真空自發性破缺所產生的,但與凝聚卻有關系,負責將能量輸送到雙重橢圓幾何的對徑點上;就好像我們從地球的北極運送物質到地球的南極,北極與南極之間的測地線不存在,但我們可以選任何一條路徑,但量子力學就不同了,由於沒有測地線,行者一定是經過所有的路徑到達對徑點;這樣就會與所有的誇克發生相互作用。由於存在這種單重橢圓幾何與雙重橢圓幾何的對偶關系,所以核力的同位旋對稱性實際上是這種對偶關系引起的相互作用,用量子色動力學的話說,是色力的剩余相互作用。
不管是色庫侖子還是行者都起著將對徑點疊合起來的作用,只是前者是對合關系,後者是輸運關系,這就要求介子一定是由一個正誇克和一個反誇克組成的無色的粒子。關於誇克禁閉還有一種更強的約束,我們知道重子是由三個誇克組成的,蓋爾曼先生很可能是童話小說看多了,叫了三聲誇克,便虛構出了誇克這種數學對象,但誇克很可能並不對應於任何真實的物理粒子,就好像費曼的鬼粒子並不對應真實的物理粒子一樣。射影空間中有一種自配極三角形,由於是自配極的,所以也滿足點線對偶性,從而與行者是兼容的;重要的是,自配級三角形的面積在幺模仿射變換下是一個不變量,所以是與狹義相對論兼容的;更重要的是,假設誇克位於自配極三角形的三個頂點上,自配極三角形的面積解釋為荷的話,荷是一個整數,不會出現每個誇克帶1/3電荷這種奇怪的事,所以也沒有自由誇克的說法。量子場論通過高能加速器擊碎原子試圖發現自由誇克的方法,這種試驗方法是值得推崇的,但量子場論的邏輯推理是有問題的;這就好像將一輛汽車經過粉碎機粉碎成無數塊慘不忍睹的碎片,然後每個碎片又會自動還原成一輛完整的汽車;一句話,QCD是還原論的,量子細胞場論是整體論的。
其實我們一直都小心翼翼的,避免與量子場論有太多矛盾的地方,我們還是有了一個容納了大自然四種基本力的統一的幾何模型,與量子場論的兼容性很好,而且比量子場論更簡單也更能貼近實驗事實;量子細胞場論沒有困擾量子場論的所謂強CP破缺問題,沒有軸矢量流的三角形反常問題。由規範勢導出的標量粒子滿足單重橢圓幾何,與矢量粒子合在一起後就變成了極矢量;行者是動態的並且滿足雙重橢圓幾何,與矢量粒子合在一起後就變成了軸矢量。當我們要求將對徑點疊合後,電弱力的兩個對合點上分別是電子和中微子,所以對於弱相互作用宇稱是不守恒的;核力的兩個對合點上分別是中子和質子,我們看到,強力中所謂的軸矢量流部分守恒在量子細胞場論中是這樣解釋的,強力並不破壞宇稱的手征對稱性。
為什麽是量子細胞?
由於量子場論中的費米子和玻色子都是沒有質量的,玻色子沒有質量是因為規範不變性的要求,而費米子沒有質量是因為手征性的問題,Goldstone玻色子在量子場論起到了中心作用,事實上,通過與量子細胞場論的對比我們下面將看到,通過Goldstone玻色子獲取質量確實可以稱為量子場論的中心法則。量子細胞場論繼承了龐加萊和Klein的思想建立了與量子場論同構的一套幾何理論,這套理論的基礎是自同構群或自守函數,這也就意謂著空間不是連續的(但至少是稠密的),甚至可以誇張的說,每兩點之間的距離都是無窮遠,這就要求所有的粒子都沒有質量,因為只有無質量的粒子才能在無窮遠之間穿越。量子場論采用蠻力的方法解決這個問題,即所謂的狄拉克δ函數,但δ函數本身的定義就是無窮大,這也是量子場論中令人頭痛的無窮大產生的根源。
由於規範場論是局域性的,量子場論需要有一個全局性的對稱性再讓它破缺來平衡局部的狀態變化,這就意謂著量子場論必須有一個無窮大的真空,我們的理論稱為量子細胞場論,但其實我們只借用了分子生物學的中心法則,因為生物是個耗散系統,對稱性是破缺的,這點與量子場論倒是很像,生命與供養它們的食物之間是不對稱的,所以非洲大草原上的角馬需要不斷遷移來尋找食物,而量子細胞場論的細胞與對偶細胞之間的對稱性是沒有破缺的,從而不需要一個無窮大的真空。
局部和全局對稱性之間的平衡到了理解強相互作用階段變得迫切起來,原因在於產生和湮滅算符的作用,核子裏聚集了大量的虛誇克和軟誇克;直接應用產生算符會生成一個半群,例如重正化群就是一個半群,群的每個元素都有一個逆元;而半群的元素卻沒有逆元,在群的作用下無法回到自身;解決的辦法只有一個就是引進兩個全局性的函子,將半群集合的全部元素映射到另外一個半群或者反之,這兩個全局性的函子在範疇論裏稱為self-adjunction算子,與量子力學中的self-adjoint算子有異曲同工的妙用,只是前者是針對二次量子化的而後者是針對一次量子化的;這兩個整體自伴算子在分子生物學中的實例不是別的,對應的正是分子生物學的中心法則,即DNA→RNA→蛋白質的生物遺傳和轉錄過程。
我們的行者哼哈子在量子細胞場論中起到的也是這種作用,行者哼哈子肩負的使命是將量子細胞的DNA從一點移到另外一點,DNA是沒有質量的因此也是沒有問題的,同時誇克也可以以無質量的方式從一點遷移到另外一點,等到了地方再根據遺傳信息重組,質量就產生了,它們只是需要在傳遞的過程中暫時凝聚一下,並不需要整個空間中都充滿了Goldstone粒子。現在回頭看看量子場論簡直充滿了誤稱,真空對稱性自發破缺是一個誤稱,所謂核力為色力的剩余相互作用也是一個誤稱;在量子細胞場論裏,核力乃是強力的局部到全局對稱性之間的平衡引發的作用力,核力的SU(2)同位旋對稱性是一種全局對稱性。也許等過幾年量子細胞場論成熟了,我們再回頭看看現在的量子細胞場論也是充滿了不成熟的或者滑稽可笑的地方,但現在我們可以肯定至少在大方向上是正確的。
不僅從狹義相對論的角度,從量子力學的角度看這種局部與全局之間的對稱性也是必然的,規範場的標量分量是一種局部的對稱性,而行者哼哈子攜帶的是全局對稱性產生的Noether標量流,但從量子力學的角度看,這兩個標量分量必然會重合到一起,就像是兩個原子通過交換電子產生共價鍵一樣,詳細的原因可以參見大牛費曼的《費曼物理學講義》第三卷有關氨分子等篇的論述,我們這裏就不再復述了。SU(2)群空間分為上下兩個不連通的空間,所以弱相互作用中宇稱是不守恒的;兩個SU(3)群的乘積恰好同構於一個反誇克存在的反SU(3)群,這就是為什麽重子總是由三個誇克組成的,強相互作用中宇稱是守恒的;兩個標量分量重合後描述了介子的性質,π介子是負宇稱的標量粒子;量子細胞場論中沒有困擾量子場論中的許多重大問題,一切都是比較完美的。
我們說兩個標量分量重合,只針對橢圓幾何的退化情形而言,對於引力而言顯然是不重合的。在人類已經完整測序的基因序列中,有一種是線蟲,這種蟲子大約由一千多個細胞組成,可以認為每個線蟲與其它線蟲都是平凡同構的,但人太復雜了,兩個人之間顯然只存在非平凡同構;不過核子不比線蟲更復雜,由於中子的質量是電子質量的一千多倍,可以設想核子大約由一千多個價誇克和海誇克組成,兩個核子之間是平凡同構的,所以從量子細胞場論的角度我們不必恐懼強相互作用的復雜性。
由於規範場論是局域性的,量子場論需要有一個全局性的對稱性再讓它破缺來平衡局部的狀態變化,這就意謂著量子場論必須有一個無窮大的真空,我們的理論稱為量子細胞場論,但其實我們只借用了分子生物學的中心法則,因為生物是個耗散系統,對稱性是破缺的,這點與量子場論倒是很像,生命與供養它們的食物之間是不對稱的,所以非洲大草原上的角馬需要不斷遷移來尋找食物,而量子細胞場論的細胞與對偶細胞之間的對稱性是沒有破缺的,從而不需要一個無窮大的真空。
局部和全局對稱性之間的平衡到了理解強相互作用階段變得迫切起來,原因在於產生和湮滅算符的作用,核子裏聚集了大量的虛誇克和軟誇克;直接應用產生算符會生成一個半群,例如重正化群就是一個半群,群的每個元素都有一個逆元;而半群的元素卻沒有逆元,在群的作用下無法回到自身;解決的辦法只有一個就是引進兩個全局性的函子,將半群集合的全部元素映射到另外一個半群或者反之,這兩個全局性的函子在範疇論裏稱為self-adjunction算子,與量子力學中的self-adjoint算子有異曲同工的妙用,只是前者是針對二次量子化的而後者是針對一次量子化的;這兩個整體自伴算子在分子生物學中的實例不是別的,對應的正是分子生物學的中心法則,即DNA→RNA→蛋白質的生物遺傳和轉錄過程。
我們的行者哼哈子在量子細胞場論中起到的也是這種作用,行者哼哈子肩負的使命是將量子細胞的DNA從一點移到另外一點,DNA是沒有質量的因此也是沒有問題的,同時誇克也可以以無質量的方式從一點遷移到另外一點,等到了地方再根據遺傳信息重組,質量就產生了,它們只是需要在傳遞的過程中暫時凝聚一下,並不需要整個空間中都充滿了Goldstone粒子。現在回頭看看量子場論簡直充滿了誤稱,真空對稱性自發破缺是一個誤稱,所謂核力為色力的剩余相互作用也是一個誤稱;在量子細胞場論裏,核力乃是強力的局部到全局對稱性之間的平衡引發的作用力,核力的SU(2)同位旋對稱性是一種全局對稱性。也許等過幾年量子細胞場論成熟了,我們再回頭看看現在的量子細胞場論也是充滿了不成熟的或者滑稽可笑的地方,但現在我們可以肯定至少在大方向上是正確的。
不僅從狹義相對論的角度,從量子力學的角度看這種局部與全局之間的對稱性也是必然的,規範場的標量分量是一種局部的對稱性,而行者哼哈子攜帶的是全局對稱性產生的Noether標量流,但從量子力學的角度看,這兩個標量分量必然會重合到一起,就像是兩個原子通過交換電子產生共價鍵一樣,詳細的原因可以參見大牛費曼的《費曼物理學講義》第三卷有關氨分子等篇的論述,我們這裏就不再復述了。SU(2)群空間分為上下兩個不連通的空間,所以弱相互作用中宇稱是不守恒的;兩個SU(3)群的乘積恰好同構於一個反誇克存在的反SU(3)群,這就是為什麽重子總是由三個誇克組成的,強相互作用中宇稱是守恒的;兩個標量分量重合後描述了介子的性質,π介子是負宇稱的標量粒子;量子細胞場論中沒有困擾量子場論中的許多重大問題,一切都是比較完美的。
我們說兩個標量分量重合,只針對橢圓幾何的退化情形而言,對於引力而言顯然是不重合的。在人類已經完整測序的基因序列中,有一種是線蟲,這種蟲子大約由一千多個細胞組成,可以認為每個線蟲與其它線蟲都是平凡同構的,但人太復雜了,兩個人之間顯然只存在非平凡同構;不過核子不比線蟲更復雜,由於中子的質量是電子質量的一千多倍,可以設想核子大約由一千多個價誇克和海誇克組成,兩個核子之間是平凡同構的,所以從量子細胞場論的角度我們不必恐懼強相互作用的復雜性。
胡思亂想
本小節純屬胡思亂想,再加上點胡言亂語;內容與對螺旋星系的理解有關;不過萬一我們的猜想有哪一條是正確的,我們倒是有可能該準備諾貝爾獎獲獎感言了。關於剩余相互作用有一點有意思的猜想,如果黑洞與我們的宇宙是對偶的關系,那麽我們的宇宙在超級宇宙中也有可能扮演一個核子的角色從而與其它的宇宙發生這種剩余相互作用,只不過這些超級強相互作用也是超級的慢動作,大約交換一個超級介子的時間是幾十億年到幾百億年,至於我們的宇宙是扮演中子還是質子的角色我們就弄不清楚了。
眾所周知,我們的銀河系以及宇宙中眾多美麗的星系都是螺旋星系;隨著我們對量子細胞引力論的更深入了解,我們發現我們的宇宙變得越來越有趣了。我們隱約看到了銀河系旋臂結構的一個可能的解釋,眾所周知銀河系的中心可能存在著一個質量巨大的黑洞,這在量子細胞引力論中意謂著太陽系沿銀河系公轉的軌道可能不是牛頓或愛因斯坦引力論推導出來的近似橢圓的軌道,而是帶著強烈的量子力學的修正;太陽系離銀河系中心時而變近、時而遠離,考慮到近動的影響,太陽系的軌道類似於一個一邊旋轉一邊飛舞的蝴蝶,或者類似於一個想告訴同伴花蜜的位置而沿著8字型軌道飛舞的蜜蜂,由眾多星星組成的銀河系在大範圍內就有可能形成旋臂結構。
經典物理圖像中,唯一與動態螺旋結構相似的是龍卷風或者經由下水管排出的水形成的旋渦;我們知道,黑洞形成的引力場類似於一個漏鬥的形狀,如果你有幸能夠到達黑洞視界的邊上,你看到的天空不會是滿天的星星,而是所有的星星都集中於你頭頂的上方;太陽帶著太陽系裏的眾多成員以每秒近三百公裏的速度沿銀河系中心公轉,需要銀河系裏至少有三千億顆恒星才能產生如此強大的引力場,而我們觀察到的恒星大約只有一千億顆,如果剩余的質量全部都是大黑洞攜帶的話,可想而知這個黑洞有多大了。如果眾多星星都是衝向大黑洞的話,就會很自然地形成螺旋結構,但這樣會帶來一個問題,眾多星星這樣排著隊、視死如歸地踏上一條不歸路,不僅與觀測事實不符,在感情上也接受不了,畢竟銀河系大約已經存在了一百多億年了。
似乎有一種很硬的背景一直提升著衝向大黑洞的星星,當星星離得與大黑洞較近時軌道便被反彈了回去,於是便形成了我們所說的蝴蝶型的軌道。這種很硬的背景很可能與自旋有關,大黑洞可能帶有強烈的自旋,但這種自旋不是廣義相對論中的Kerr黑洞的自旋而是量子世界的自旋;在量子世界裏所有的粒子都帶有自旋,這種自旋是在內部空間裏的一種自旋,所以不是Kerr黑洞的自旋。由於引力與強力有很多相似之處,借助強力我們可以理解一些引力的現象,但引力還是比強力復雜得多,愛因斯坦的廣義相對論將引力場過於簡單化了。
我們已經將強相互作用中的真空超導化機制排除了,這就意謂著如果量子細胞場論對強作用力的看法是對的,特Hooft等一系列大牛的看法便被否定了,不知道這些大牛們會不會向我們扔磚頭:-)不過黑洞中確實應該是超導化的,在我們看來黑洞的視界溫度接近絕對0度,可見黑洞內的對稱性自發破缺是不可避免的,於是會產生大規模的集體激發現象,引力的Goldstone玻色子自然會出現從而引發大範圍的引力自旋波。引力自旋波的效應只有當星星離大黑洞較近時才較為明顯,而且按照我們的分析引發的效應應該是排斥性的,也就是借助於引力場強張量的對偶場強張量發揮作用的。另外,黑洞也會是一個超級哼哈子,哼哈子的作用在於使各個星星的軌道排列有序,就像它們在強力中扮演的角色一樣;只有到我們對量子細胞引力有了更深入的了解並進行精確的計算後才能知道到底發生了什麽。
眾所周知,我們的銀河系以及宇宙中眾多美麗的星系都是螺旋星系;隨著我們對量子細胞引力論的更深入了解,我們發現我們的宇宙變得越來越有趣了。我們隱約看到了銀河系旋臂結構的一個可能的解釋,眾所周知銀河系的中心可能存在著一個質量巨大的黑洞,這在量子細胞引力論中意謂著太陽系沿銀河系公轉的軌道可能不是牛頓或愛因斯坦引力論推導出來的近似橢圓的軌道,而是帶著強烈的量子力學的修正;太陽系離銀河系中心時而變近、時而遠離,考慮到近動的影響,太陽系的軌道類似於一個一邊旋轉一邊飛舞的蝴蝶,或者類似於一個想告訴同伴花蜜的位置而沿著8字型軌道飛舞的蜜蜂,由眾多星星組成的銀河系在大範圍內就有可能形成旋臂結構。
經典物理圖像中,唯一與動態螺旋結構相似的是龍卷風或者經由下水管排出的水形成的旋渦;我們知道,黑洞形成的引力場類似於一個漏鬥的形狀,如果你有幸能夠到達黑洞視界的邊上,你看到的天空不會是滿天的星星,而是所有的星星都集中於你頭頂的上方;太陽帶著太陽系裏的眾多成員以每秒近三百公裏的速度沿銀河系中心公轉,需要銀河系裏至少有三千億顆恒星才能產生如此強大的引力場,而我們觀察到的恒星大約只有一千億顆,如果剩余的質量全部都是大黑洞攜帶的話,可想而知這個黑洞有多大了。如果眾多星星都是衝向大黑洞的話,就會很自然地形成螺旋結構,但這樣會帶來一個問題,眾多星星這樣排著隊、視死如歸地踏上一條不歸路,不僅與觀測事實不符,在感情上也接受不了,畢竟銀河系大約已經存在了一百多億年了。
似乎有一種很硬的背景一直提升著衝向大黑洞的星星,當星星離得與大黑洞較近時軌道便被反彈了回去,於是便形成了我們所說的蝴蝶型的軌道。這種很硬的背景很可能與自旋有關,大黑洞可能帶有強烈的自旋,但這種自旋不是廣義相對論中的Kerr黑洞的自旋而是量子世界的自旋;在量子世界裏所有的粒子都帶有自旋,這種自旋是在內部空間裏的一種自旋,所以不是Kerr黑洞的自旋。由於引力與強力有很多相似之處,借助強力我們可以理解一些引力的現象,但引力還是比強力復雜得多,愛因斯坦的廣義相對論將引力場過於簡單化了。
我們已經將強相互作用中的真空超導化機制排除了,這就意謂著如果量子細胞場論對強作用力的看法是對的,特Hooft等一系列大牛的看法便被否定了,不知道這些大牛們會不會向我們扔磚頭:-)不過黑洞中確實應該是超導化的,在我們看來黑洞的視界溫度接近絕對0度,可見黑洞內的對稱性自發破缺是不可避免的,於是會產生大規模的集體激發現象,引力的Goldstone玻色子自然會出現從而引發大範圍的引力自旋波。引力自旋波的效應只有當星星離大黑洞較近時才較為明顯,而且按照我們的分析引發的效應應該是排斥性的,也就是借助於引力場強張量的對偶場強張量發揮作用的。另外,黑洞也會是一個超級哼哈子,哼哈子的作用在於使各個星星的軌道排列有序,就像它們在強力中扮演的角色一樣;只有到我們對量子細胞引力有了更深入的了解並進行精確的計算後才能知道到底發生了什麽。
中心法則
我們認出這正是規範場論賴以生存的根本大法,所以稱之為中心法則也不為過。半個多世紀前,Weyl和楊振寧等人將整體對稱性提升到局部對稱性,規範場便自動地冒了出來;今天我們反其道而行之,將二次量子化後的局域對稱性提升到整體對稱性,核力的同位旋對稱性便自動地冒了出來;難道這不是很美妙嗎? 我們事實上已經提開了質子自旋之迷,其實在量子場論界所謂核子自旋危機這個名詞已經由來已久,早就失去它應有的緊迫感;量子場論中核子失蹤的自旋是哼哈玻色子攜帶的;那麽自旋為0的哼哈子是如何攜帶核子的自旋呢? 答案還是與對偶性有關,在射影空間中移動一段距離和旋轉一些角度是對偶的,所以標量與旋量也是對偶的,這就是量子細胞場論的好處,一旦我們知道一個命題是成立的,那麽它的對偶命題便自動成立。
通過與細胞物理學的類比,我們可以分析出量子場論的中心法則遺漏了些什麽。產生和湮滅算符是一對自伴的算符,與DNA→RNA→蛋白質的細胞生物學的中心法則確實是相似的;但直接應用這個規則生成的是一個遞歸可枚舉集,這個集合裏有大量的不可判定的命題,比如有個南京人說所有的南京人都說謊,這句話符合語法但導出的卻是一個自相矛盾的結論,在邏輯上是沒有意義的;因此在邏輯上我們只關心遞歸集,遞歸集裏的語句不僅符合語法而且都是有意義的。要想讓細胞遞歸就必須聯系上細胞周期,我們知道細胞周期類似於量子場論的相位因子,規範場是一個相位因子場,沒有了相位因子就沒有了量子的特點,量子場論與經典力學並沒有區別。
所以完整的中心法則必須聯系上相位因子,這類似於細胞通過分裂自我繁殖的過程,僅有誇克的復制是不夠的,必須聯系上核子的DNA的復制。狹義相對論否認了真空中的以太說,量子細胞場論的看法也否認了量子場論中現代版的以太說。現在讓我們看看在一個相位轉過360度的周期內都發生了什麽,這與量子力學的幾率概念是對應的,這時量子細胞從一點遷移到時空中的下一點,我們讓時空暫時破缺一下,就是從四維暫時破缺到三維,到了下一點再恢復成四維,我們認出這正是量子場論中通過軸矢量粒子獲取質量的機制;所以粒子的質量便產生了,到了下一點後,量子細胞再來一個細胞分裂,讓對偶細胞在下一個下一點等著量子細胞。
我們看到這種獲取質量的機制是不需要真空中有大量粒子凝聚形成的背景場的,這樣我們就擯棄了現代版的以太說。重要的是,這種機制與德布羅意的E=hω假說是兼容的,我們可以認為ω就是量子細胞的周期,這樣我們就將量子力學與愛因斯坦的質能關系式統一了起來,我們看到量子細胞場論與狹義相對論和量子力學的基本假設確實都是兼容的;物理學經過了一個多世紀的發展,終於從終點又回到了起點,伴隨著的是人類認識上的巨大進步。
通過與細胞物理學的類比,我們可以分析出量子場論的中心法則遺漏了些什麽。產生和湮滅算符是一對自伴的算符,與DNA→RNA→蛋白質的細胞生物學的中心法則確實是相似的;但直接應用這個規則生成的是一個遞歸可枚舉集,這個集合裏有大量的不可判定的命題,比如有個南京人說所有的南京人都說謊,這句話符合語法但導出的卻是一個自相矛盾的結論,在邏輯上是沒有意義的;因此在邏輯上我們只關心遞歸集,遞歸集裏的語句不僅符合語法而且都是有意義的。要想讓細胞遞歸就必須聯系上細胞周期,我們知道細胞周期類似於量子場論的相位因子,規範場是一個相位因子場,沒有了相位因子就沒有了量子的特點,量子場論與經典力學並沒有區別。
所以完整的中心法則必須聯系上相位因子,這類似於細胞通過分裂自我繁殖的過程,僅有誇克的復制是不夠的,必須聯系上核子的DNA的復制。狹義相對論否認了真空中的以太說,量子細胞場論的看法也否認了量子場論中現代版的以太說。現在讓我們看看在一個相位轉過360度的周期內都發生了什麽,這與量子力學的幾率概念是對應的,這時量子細胞從一點遷移到時空中的下一點,我們讓時空暫時破缺一下,就是從四維暫時破缺到三維,到了下一點再恢復成四維,我們認出這正是量子場論中通過軸矢量粒子獲取質量的機制;所以粒子的質量便產生了,到了下一點後,量子細胞再來一個細胞分裂,讓對偶細胞在下一個下一點等著量子細胞。
我們看到這種獲取質量的機制是不需要真空中有大量粒子凝聚形成的背景場的,這樣我們就擯棄了現代版的以太說。重要的是,這種機制與德布羅意的E=hω假說是兼容的,我們可以認為ω就是量子細胞的周期,這樣我們就將量子力學與愛因斯坦的質能關系式統一了起來,我們看到量子細胞場論與狹義相對論和量子力學的基本假設確實都是兼容的;物理學經過了一個多世紀的發展,終於從終點又回到了起點,伴隨著的是人類認識上的巨大進步。
微分幾何與統一場論
纖維叢與自對偶
Felix Klein在1871年闡述了埃爾朗根綱領;這就是幾何學定義為研究有連續自同構群的空間,例如歐氏空間具有剛體運動群,射影空間具有射影直射變換群等。其中包括非歐幾何學,根據Klein的觀點,非歐幾何學只要在空間中有一個所謂二次的超曲面,討論在所有的投影變換下,使這個二次超曲面不變。例如:在平面上有一個圓周,非歐幾何就是要討論在投影變換下圓周仍不改變的性質。因此根據Klein的觀點,非歐幾何學就變得極易處理。
Klein的埃爾朗根綱領與狹義相對論完美地結合,狹義相對論中的一個原理是洛倫茲群下場方程的不變性,這導致了Klein這們處於世紀轉折時期最有影響的德國數學家成為狹義相對論最早的支持者之一。洛倫茲結構在相對論中起了基本的作用,它還有幾何學的解釋。當我們研究空間中球的幾何時,將球變為球的所有接觸變換構成一個15參數群,而把平面變為平面的變換構成一個10參數的子群,後者與4個變量的洛倫茲群同構,所導致的幾何學就是拉蓋爾的球幾何學。
Klein的埃爾朗根綱領的成功自然地引起了Klein空間或現在稱之為齊性空間中的微分幾何的研究;跟隨Weyl之後產生了維布倫的相對論的射影理論,維布倫的理論是四維的,但切射影空間有五維的齊次坐標,維布倫的射影理論在幾何上是簡單的,他的出發點是空間的路徑,它們是帶電粒子的軌線;道路空間幾何學涉及到射影聯絡。
在Klein制訂埃爾朗根綱領時,已觀察到黎曼幾何並不包括在內,因為一個一般的黎曼空間除恒等變換外並不含有其他等長變換。Elie Cartan在他的主要論文《仿射聯絡的流形及廣義相對論理論》中給出仿射聯絡的論述以及它向有撓率聯絡的推廣;它比仿射聯絡論的內容更豐富;它的思想可以容易地推廣到任何李群的纖維叢的聯絡理論中去。
用幾何的話來說,仿射聯絡是一族仿射空間即纖維,它們由一個基底空間所參數化,使得這一族仿射空間是局部平凡的,並且有一個纖維沿著基底空間的曲線展開的法則,使線性關系得以保持。類似地,我們可以把Klein空間當作纖維並且用作用於Klein空間的李群來代替完全線性群,並且也有一個對應的展開法則;Cartan稱這樣的結構為一般空間。一般來說,這個聯絡是非和樂的,即展開依賴於基底空間的曲線。換句話說,沿一條閉曲線作展開時,空間並不回到原來的位置,它的變差是由聯絡的曲率來度量的;顯然,Klein空間本身是一個曲率恒等於0的一般空間。從Cartan的觀點來看,黎曼空間是一個以歐氏空間為纖維的空間,並且具有Levi-Civita聯絡;這解決了微分幾何中的一個基礎的問題,因為這樣就有了一個概念,它包括了Klein空間、黎曼空間以及這兩種空間的推廣。
Klein的埃爾朗根綱領與狹義相對論完美地結合,狹義相對論中的一個原理是洛倫茲群下場方程的不變性,這導致了Klein這們處於世紀轉折時期最有影響的德國數學家成為狹義相對論最早的支持者之一。洛倫茲結構在相對論中起了基本的作用,它還有幾何學的解釋。當我們研究空間中球的幾何時,將球變為球的所有接觸變換構成一個15參數群,而把平面變為平面的變換構成一個10參數的子群,後者與4個變量的洛倫茲群同構,所導致的幾何學就是拉蓋爾的球幾何學。
Klein的埃爾朗根綱領的成功自然地引起了Klein空間或現在稱之為齊性空間中的微分幾何的研究;跟隨Weyl之後產生了維布倫的相對論的射影理論,維布倫的理論是四維的,但切射影空間有五維的齊次坐標,維布倫的射影理論在幾何上是簡單的,他的出發點是空間的路徑,它們是帶電粒子的軌線;道路空間幾何學涉及到射影聯絡。
在Klein制訂埃爾朗根綱領時,已觀察到黎曼幾何並不包括在內,因為一個一般的黎曼空間除恒等變換外並不含有其他等長變換。Elie Cartan在他的主要論文《仿射聯絡的流形及廣義相對論理論》中給出仿射聯絡的論述以及它向有撓率聯絡的推廣;它比仿射聯絡論的內容更豐富;它的思想可以容易地推廣到任何李群的纖維叢的聯絡理論中去。
用幾何的話來說,仿射聯絡是一族仿射空間即纖維,它們由一個基底空間所參數化,使得這一族仿射空間是局部平凡的,並且有一個纖維沿著基底空間的曲線展開的法則,使線性關系得以保持。類似地,我們可以把Klein空間當作纖維並且用作用於Klein空間的李群來代替完全線性群,並且也有一個對應的展開法則;Cartan稱這樣的結構為一般空間。一般來說,這個聯絡是非和樂的,即展開依賴於基底空間的曲線。換句話說,沿一條閉曲線作展開時,空間並不回到原來的位置,它的變差是由聯絡的曲率來度量的;顯然,Klein空間本身是一個曲率恒等於0的一般空間。從Cartan的觀點來看,黎曼空間是一個以歐氏空間為纖維的空間,並且具有Levi-Civita聯絡;這解決了微分幾何中的一個基礎的問題,因為這樣就有了一個概念,它包括了Klein空間、黎曼空間以及這兩種空間的推廣。
纖維叢與自對偶
歐氏空間只有一個切空間,現在的空間情況復雜了一些,每點都有一個切空間,但都是平坦空間;這個現象在幾何上有一個重大的發展,就是把切空間豎起來;我們就叫它為纖維叢,或叫矢量空間叢。Maxwell方程就是建立在一個矢量叢上,這個纖維叢是復數空間;現在是一把復線,你如果能有法子從這個纖維到另外一個纖維有一個平行性的話,就能立刻得到Maxwell方程。現在纖維叢上有一個平行性,這個平行性的微分,等於電磁場的強度F,然後把這個F再求它的余微分的話,就得到流矢量J。用下面兩個簡單的式子,就把Maxwell方程寫出來了,F=dA,δF=J。在電磁學裏,要把Maxwell全部寫出來的話,書上往往是一整頁;其實簡單地說,也就是平行性的微分是場的強度,而場的強度的余微分就是流矢量。
所以Maxwell方程就是建立在一個復的纖維叢上,你怎樣把每個纖維拼起來呢,需要群的概念,即U(1)群,群裏有一個運算,把一個纖維可以挪到其他一個纖維,這是個可交換的群,叫做Abel群。歐氏平面可以引進復坐標便成為復線,它的歐氏度量變為埃爾米特度量;所以電磁學的基礎是洛倫茲流形上的埃爾米特線叢。電磁學的概念可以推廣到高維的復矢量空間叢和埃爾米特空間叢。楊振寧先生用到一個非Abel群SU(2)群。用SU(2)聯絡,把同樣的方程寫出來,就是Yang-Mills方程,F=dA,δF=J。
在物理上有一個Bohm-Aharonov實驗,就是說:電磁學中的Maxwell方程寫成那樣的形式是不對的,因為它沒有把所有的電磁現象都表示出來,應該利用圓周叢聯絡A,F=dA才是描寫所有電磁現象的方程式。Bohm-Aharonov實驗是這樣的,有一個內有磁場的圓筒,外面沒有磁場,而在圓筒的外圍接有線圈,那麽圓筒內的磁場,便和通電的路徑有關。
人們發現,這些微分幾何概念很可能是統一場論的數學基礎;研究同位旋時,Yang-Mills所用的本質上是SU(2)叢的一個聯絡,從聯絡可以定義作用量。四維歐氏空間上的SU(2)叢中使作用量取最小值的聯絡被稱為瞬子;它的曲率有一個簡單的表達式,稱為自對偶關系;從而瞬子是Yang-Mills場的自對偶解。當四維歐氏空間緊致化成為一個四維球時,SU(2)叢除了一個同構外由一個拓撲量子數決定;對於給定的拓撲量子數,四維球上曲率為自對偶的聯絡的集合是一個稱為模或參數空間的光滑流形。
阿蒂亞和Ward註意到,自對偶的Yang-Mills場可以很好地納入彭羅斯的扭量方案。瞬子通過以下的結果表明它和愛因斯坦的關系;群SO(4)局部同構於SU(2)╳SU(2),所以四維黎曼流形M上的黎曼度量通過投影給出一個SU(2)叢的聯絡。依投影的方法而區分,M為愛因斯坦流形的充要條件是這些聯絡為自對偶或反自對偶。我們需要指出的是,叢和聯絡這兩個幾何概念是非常簡潔的,我們相信愛因斯坦會喜歡它們。
所以Maxwell方程就是建立在一個復的纖維叢上,你怎樣把每個纖維拼起來呢,需要群的概念,即U(1)群,群裏有一個運算,把一個纖維可以挪到其他一個纖維,這是個可交換的群,叫做Abel群。歐氏平面可以引進復坐標便成為復線,它的歐氏度量變為埃爾米特度量;所以電磁學的基礎是洛倫茲流形上的埃爾米特線叢。電磁學的概念可以推廣到高維的復矢量空間叢和埃爾米特空間叢。楊振寧先生用到一個非Abel群SU(2)群。用SU(2)聯絡,把同樣的方程寫出來,就是Yang-Mills方程,F=dA,δF=J。
在物理上有一個Bohm-Aharonov實驗,就是說:電磁學中的Maxwell方程寫成那樣的形式是不對的,因為它沒有把所有的電磁現象都表示出來,應該利用圓周叢聯絡A,F=dA才是描寫所有電磁現象的方程式。Bohm-Aharonov實驗是這樣的,有一個內有磁場的圓筒,外面沒有磁場,而在圓筒的外圍接有線圈,那麽圓筒內的磁場,便和通電的路徑有關。
人們發現,這些微分幾何概念很可能是統一場論的數學基礎;研究同位旋時,Yang-Mills所用的本質上是SU(2)叢的一個聯絡,從聯絡可以定義作用量。四維歐氏空間上的SU(2)叢中使作用量取最小值的聯絡被稱為瞬子;它的曲率有一個簡單的表達式,稱為自對偶關系;從而瞬子是Yang-Mills場的自對偶解。當四維歐氏空間緊致化成為一個四維球時,SU(2)叢除了一個同構外由一個拓撲量子數決定;對於給定的拓撲量子數,四維球上曲率為自對偶的聯絡的集合是一個稱為模或參數空間的光滑流形。
阿蒂亞和Ward註意到,自對偶的Yang-Mills場可以很好地納入彭羅斯的扭量方案。瞬子通過以下的結果表明它和愛因斯坦的關系;群SO(4)局部同構於SU(2)╳SU(2),所以四維黎曼流形M上的黎曼度量通過投影給出一個SU(2)叢的聯絡。依投影的方法而區分,M為愛因斯坦流形的充要條件是這些聯絡為自對偶或反自對偶。我們需要指出的是,叢和聯絡這兩個幾何概念是非常簡潔的,我們相信愛因斯坦會喜歡它們。
Cartan幾何
纖維叢的一個簡單例子就是三維歐氏空間中所有與某一球面相切的非零向量形成的流形。這是個拓撲流形,雖然很特殊;然而結果表明,具有類似性質的流形在拓撲學在微分幾何的應用中發揮了重要的作用。
廣義相對論用到的是黎曼幾何,黎曼幾何中一個重要的事實就是,你不僅要考慮黎曼流形本身而且必須考慮流形上的纖維叢;我們的方法是,直接考慮纖維叢;而通常的張量分析方法通過強調局部坐標系來回避它。大量的幾何研究都是關於那些在局部坐標變換下服從簡單規律的問題;關於局部問題,Elie Cartan對此當然是很熟悉的,他為他的幾何實在,仿射聯絡、射影聯絡、正則聯絡等等的一般理論引進了切空間的概念。Cartan意義下的切空間並不總是切向量空間,這構成了難以理解他的工作的原因之一。
我們的問題是研究微分流形上以局部坐標系形式給出的幾何實在,這樣的問題一般總有可能在某種意義下定義在與該流形關聯的一個自然的纖維叢上。於是這個幾何實在以唯一的方式在纖維叢中定義了一組線性微分形式,對於黎曼幾何來說,這個自然的纖維叢就是流形上全部標架所形成的空間,而相應的微分形式給出的實際上是Levi-Civita平行;關聯的纖維叢的性質由解決所謂等價問題而得到最佳的確定。
我們的問題是研究微分流形上以局部坐標系形式給出的幾何實在,這樣的問題一般總有可能在某種意義下定義在與該流形關聯的一個自然的纖維叢上。於是這個幾何實在以唯一的方式在纖維叢中定義了一組線性微分形式,對於黎曼幾何來說,這個自然的纖維叢就是流形上全部標架所形成的空間,而相應的微分形式給出的實際上是Levi-Civita平行;關聯的纖維叢的性質由解決所謂等價問題而得到最佳的確定。
| 一般情況 | 特殊例子 |
| 纖維叢(Circular Point) | 球面的切向量流形 |
| 纖維叢的點 | 切向量 |
| 底空間 | 球面 |
| 纖維 | 同一基點上的向量 |
| 投射 | 把切向量映射到其基點 |
| 纖維中的變換群 | 同一基點的向量空間中的仿射或旋轉群 |
纖維叢的一個簡單例子就是三維歐氏空間中所有與某一球面相切的非零向量形成的流形。這是個拓撲流形,雖然很特殊;然而結果表明,具有類似性質的流形在拓撲學在微分幾何的應用中發揮了重要的作用。
物質場與黎曼幾何
我們的馬德西特宇宙模型對物質場而言是正常曲率的,相當於隱含了一個宇宙學常數,但這個宇宙學常數與愛因斯坦的宇宙學常數方向上是相互垂直的;這就是量子細胞引力論與廣義相對論的不同之處。廣義相對論將引力論過分簡單化了,反而引出了很多病態的結論,正所謂欲速則不達;量子細胞引力論引入了許多現代量子場論中的概念,所得到的結論卻常常是意外的簡單;物質場所在的正常曲率空間的拓撲量子數是1,這符合我們原先將我們的宇宙看成是超級宇宙中的一個超級基本粒子的想法。雖然量子細胞引力論與廣義相對論對黎曼幾何的解釋有所不同,但黎曼幾何卻是兩套理論共同的基礎,所以我們有必要先學習一下黎曼幾何的知識。
Gauss在1827年的文章中,對於一個由測地線構成的三角形,證明了一條關於曲率的著名定理。設K是一個曲面的可變曲率,於是∫∫KdA是這個曲率在面積A上的積分;Gauss的定理用於這三角形時說∫∫KdA等於三個角之和減去π;這就是說,在一個測地三角形上曲率的積分等於三個角之和超過180度的盈量,或在三個角之和小於180度量,等於三個角之和不足180度的虧量;Gauss說這個定理應該算是一個最精美的定理;這個結果推廣了Lambert的定理,後者斷言球面三角形的面積等於它的球面盈量與半徑平方之積,因為在一個球面三角形上K是常數且等於半徑平方的倒數。
Riemann提出的空間的幾何並不只是Gauss的微分幾何的推廣,他重新考慮了研究空間的整個途徑。Riemann在完成了他的n維幾何的一般研究,並說明如何引進曲率以後,進而考慮特定的流形,在這種流形上,有限的空間形式應當能夠移動,而不改變其大小或形狀,並且應當能夠按任意方向旋轉;這就把他引到常曲率空間。當在一點所有曲率的測度都相同,並且等於其它任何點的所有曲率的測度時,我們得到Riemann稱之為常曲率的流形;在這種流形上可以討論全等的圖形。如果α是曲率的測度,常曲率流形上無窮小距離元素應作相應的改變。
對於正的常曲率α等於某個超半徑a的平方,並且n=3的情形,由於Gauss的工作,可以得到一種三維的球面幾何,雖然不能把它形象化;這個空間在廣度上有限但是無界;在其中所有的測地線都是定長,等於2π/a,並且回到它們自身。如果不考慮時間維而只考慮三個空間維,則馬德西特時空中物質場的分布基於的正是這種模型,並且我們已經自然地考慮了引力的潮汐效應;如果考慮了時空的對偶性,則很自然地可以推廣到四維時空的情形。至於Riemann是否認為常數正曲率曲面上的測地線都交於一點或兩點,實際上是不清楚的。
Felix Klein後來指出,這裏涉及到兩種不同的幾何。經常,兩個或者更多的不同的幾何有同構的自同構群。這就產生了從愛爾蘭根綱領的抽象群解讀出具體的幾何的問題。一個例子:可定向(也就是說,反射是除外的)橢圓幾何(也就是,把n維球面相對點等同的曲面)和可定向球面幾何(同樣的非歐幾裏得幾何,但是相對的點沒有等同起來)有同構的自同構群,偶數n的SO(n+1)。這兩個看起來不同。但是事實上,這兩個幾何緊密相關,以一種可以精確描述的方式。1886年,Friedrich Schur證明了一個後來以他的名字命名的定理,根據Riemann提出曲率概念的思路,Schur講到空間的一個定向的曲率,這種定向由一束測地線μα+λβ確定,其中α和β是從一點出發的兩條測地線的方向;這個束構成一個曲面並且有一個Gauss曲率,Schur稱之為這個定向的Riemann曲率。他於是斷言,如果空間的Riemann曲率在每一點都同定向無關,則Riemann曲率在全空間是常數;因此,這種流形是一個常曲率空間。由此可見,從Schur的想法發展到量子細胞引力論中的橢圓叢空間又是一種自然的推廣。
Gauss在1827年的文章中,對於一個由測地線構成的三角形,證明了一條關於曲率的著名定理。設K是一個曲面的可變曲率,於是∫∫KdA是這個曲率在面積A上的積分;Gauss的定理用於這三角形時說∫∫KdA等於三個角之和減去π;這就是說,在一個測地三角形上曲率的積分等於三個角之和超過180度的盈量,或在三個角之和小於180度量,等於三個角之和不足180度的虧量;Gauss說這個定理應該算是一個最精美的定理;這個結果推廣了Lambert的定理,後者斷言球面三角形的面積等於它的球面盈量與半徑平方之積,因為在一個球面三角形上K是常數且等於半徑平方的倒數。
Riemann提出的空間的幾何並不只是Gauss的微分幾何的推廣,他重新考慮了研究空間的整個途徑。Riemann在完成了他的n維幾何的一般研究,並說明如何引進曲率以後,進而考慮特定的流形,在這種流形上,有限的空間形式應當能夠移動,而不改變其大小或形狀,並且應當能夠按任意方向旋轉;這就把他引到常曲率空間。當在一點所有曲率的測度都相同,並且等於其它任何點的所有曲率的測度時,我們得到Riemann稱之為常曲率的流形;在這種流形上可以討論全等的圖形。如果α是曲率的測度,常曲率流形上無窮小距離元素應作相應的改變。
對於正的常曲率α等於某個超半徑a的平方,並且n=3的情形,由於Gauss的工作,可以得到一種三維的球面幾何,雖然不能把它形象化;這個空間在廣度上有限但是無界;在其中所有的測地線都是定長,等於2π/a,並且回到它們自身。如果不考慮時間維而只考慮三個空間維,則馬德西特時空中物質場的分布基於的正是這種模型,並且我們已經自然地考慮了引力的潮汐效應;如果考慮了時空的對偶性,則很自然地可以推廣到四維時空的情形。至於Riemann是否認為常數正曲率曲面上的測地線都交於一點或兩點,實際上是不清楚的。
Felix Klein後來指出,這裏涉及到兩種不同的幾何。經常,兩個或者更多的不同的幾何有同構的自同構群。這就產生了從愛爾蘭根綱領的抽象群解讀出具體的幾何的問題。一個例子:可定向(也就是說,反射是除外的)橢圓幾何(也就是,把n維球面相對點等同的曲面)和可定向球面幾何(同樣的非歐幾裏得幾何,但是相對的點沒有等同起來)有同構的自同構群,偶數n的SO(n+1)。這兩個看起來不同。但是事實上,這兩個幾何緊密相關,以一種可以精確描述的方式。1886年,Friedrich Schur證明了一個後來以他的名字命名的定理,根據Riemann提出曲率概念的思路,Schur講到空間的一個定向的曲率,這種定向由一束測地線μα+λβ確定,其中α和β是從一點出發的兩條測地線的方向;這個束構成一個曲面並且有一個Gauss曲率,Schur稱之為這個定向的Riemann曲率。他於是斷言,如果空間的Riemann曲率在每一點都同定向無關,則Riemann曲率在全空間是常數;因此,這種流形是一個常曲率空間。由此可見,從Schur的想法發展到量子細胞引力論中的橢圓叢空間又是一種自然的推廣。
細胞量子化
細胞量子化的線索來自於幾個方面。第一條線索是對狹義相對論完備性的考查迫使我們進入射影叢的空間;第二條線索來自於規範場將主叢上聯絡作為基本幾何量的考慮,前面我們已經說得很多了。第三條線索則直接來自於矩陣力學和正則量子化方法,正則量子化方法牽涉到對偶場量的量子化,為了從經典理論過渡到量子理論,我們必須把坐標及其共軛動量看成是作用在可能的物理態Hilbert空間中的算符,再對它們加上量子條件,這就是正則量子化方法;這些場函數遵從由拉氏量導出的微分波動方程;這樣作了以後,我們就得到了Bohr互被意義下的電磁場的粒子解釋。
要得到一個具有微分波動傳播的理論,場函數必須是連續參數空間和時間的連續函數,場在一點的改變由無限鄰近於該點的那些場的性質來決定。對於大多數經典波動場,這樣的描述是個理想化,它只在距離大於表征介質顆粒大小的特征長度時成立。如果我們簡單地保持這樣的觀念,即借助連續時空坐標的微觀表述是Lorentz不變的,那麽我們預期相互作用通過時空的傳播速度不大於光速,這種微觀因果性的概念強烈地迫使我們進入場的概念。
高能範圍內狹義相對論的正確性有著肯定的證據,而且也已有肯定的證據表明,微觀因果性概念是一個正確的概念。正則量子化方法有一個缺點,即時間與空間不是平權的,時間坐標帶有特殊的地位,所以不太適合狹義相對論體系;當然可以用路徑積分量子化方法來克服這個缺點,但路徑積分量子化方法非常復雜,並且也只適用於計算高斯分布這種特殊的情形;細胞量子化方法是另一種克服這個缺點的辦法,在射影對偶空間中時間和空間是平權的,而射影叢空間中恰恰有大量的對偶性存在。電磁場為細胞量子化方法提供了一個佐證,電磁場恰好是自對偶的,但這種自對偶性只對無源的自由場成立;非齊次的Maxwell方程是有源方程,對偶性被破壞了,所以我們引用了射影空間中慣用的引入無窮遠元素的辦法來解決這種問題,電荷變成了射影空間中的無窮遠元素,補充了這個仿射補丁後,整個空間都是完備的,對偶性在空間中的每一點都嚴格成立。
要得到一個具有微分波動傳播的理論,場函數必須是連續參數空間和時間的連續函數,場在一點的改變由無限鄰近於該點的那些場的性質來決定。對於大多數經典波動場,這樣的描述是個理想化,它只在距離大於表征介質顆粒大小的特征長度時成立。如果我們簡單地保持這樣的觀念,即借助連續時空坐標的微觀表述是Lorentz不變的,那麽我們預期相互作用通過時空的傳播速度不大於光速,這種微觀因果性的概念強烈地迫使我們進入場的概念。
高能範圍內狹義相對論的正確性有著肯定的證據,而且也已有肯定的證據表明,微觀因果性概念是一個正確的概念。正則量子化方法有一個缺點,即時間與空間不是平權的,時間坐標帶有特殊的地位,所以不太適合狹義相對論體系;當然可以用路徑積分量子化方法來克服這個缺點,但路徑積分量子化方法非常復雜,並且也只適用於計算高斯分布這種特殊的情形;細胞量子化方法是另一種克服這個缺點的辦法,在射影對偶空間中時間和空間是平權的,而射影叢空間中恰恰有大量的對偶性存在。電磁場為細胞量子化方法提供了一個佐證,電磁場恰好是自對偶的,但這種自對偶性只對無源的自由場成立;非齊次的Maxwell方程是有源方程,對偶性被破壞了,所以我們引用了射影空間中慣用的引入無窮遠元素的辦法來解決這種問題,電荷變成了射影空間中的無窮遠元素,補充了這個仿射補丁後,整個空間都是完備的,對偶性在空間中的每一點都嚴格成立。
經典場論中的對偶性
對偶性存在的第一個例子來自於經典場論;自然界中沒有一個粒子嚴格服從Klein-Gordan方程,只有當某些對偶性存在的情況下才近似服從Klein-Gordan方程。當我們研究波導中的電磁輻射及地球電離層中的電磁波時,我們會碰到與Klein-Gordan方程一樣的色散關系。中性等離子體由帶有一些電離分子的中性分子氣體所組成;每個一階電離分子就是推動一個負電子的正離子。地球的電離層是一層空氣,它含有許多電離的空氣分子;空氣分子的電離往往是由於吸收了太陽發射的紫外光量子。因為平均來說等離子體是中性的,它不能作為產生靜電場的源。
可是,等離子體在任何一瞬間,可能在某一個區域電荷稍許過剩,而在相鄰的另一區域電荷相應地減少,這樣就在等離子體中產生電場。在電場作用下,離子沿一個方向加速,電子則沿相反方向加速。電荷運動的方向,趨向於去消滅那些產生電場的電荷的過剩或過少;於是這裏有了一種恢復力。當電荷過剩的數量被抵消為0時,相應的電場也變為零,這時離子和電子已獲得了速度;慣性使得它們衝過頭,造成新的電荷過剩和不足,正負號與原來的相反。
在粒子的量子描述中,相對論性德布羅依波的色散關系也服從同樣的方程,即Klein-Gordan方程。我們看到電荷與質量可以具有對偶關系,如果我們假設愛因斯坦的質能關系式反映的是質能對稱性背後的質能對偶性,則自然就可以得到單重橢圓幾何與雙重橢圓幾何對偶的結論,用物理學語言說就是極矢量與軸矢量對偶。我們看到,具備了這樣一種對偶關系後,電磁力→弱力→強力→核力這樣一種導出的鏈式規則便自然呈現在我們面前;電磁場中只有極矢量,不存在這種對偶關系,所以光子是沒有質量的;W和Z玻色子存在這種對偶關系,便有了質量。
可是,等離子體在任何一瞬間,可能在某一個區域電荷稍許過剩,而在相鄰的另一區域電荷相應地減少,這樣就在等離子體中產生電場。在電場作用下,離子沿一個方向加速,電子則沿相反方向加速。電荷運動的方向,趨向於去消滅那些產生電場的電荷的過剩或過少;於是這裏有了一種恢復力。當電荷過剩的數量被抵消為0時,相應的電場也變為零,這時離子和電子已獲得了速度;慣性使得它們衝過頭,造成新的電荷過剩和不足,正負號與原來的相反。
在粒子的量子描述中,相對論性德布羅依波的色散關系也服從同樣的方程,即Klein-Gordan方程。我們看到電荷與質量可以具有對偶關系,如果我們假設愛因斯坦的質能關系式反映的是質能對稱性背後的質能對偶性,則自然就可以得到單重橢圓幾何與雙重橢圓幾何對偶的結論,用物理學語言說就是極矢量與軸矢量對偶。我們看到,具備了這樣一種對偶關系後,電磁力→弱力→強力→核力這樣一種導出的鏈式規則便自然呈現在我們面前;電磁場中只有極矢量,不存在這種對偶關系,所以光子是沒有質量的;W和Z玻色子存在這種對偶關系,便有了質量。
量子細胞場論的基本定理
量子場論中存在著大量的對偶性;雖然量子細胞場論與量子場論對一些重大問題的看法不同,在牽涉到對偶性關系上兩者基本上是同構的;量子細胞場論可以以這些量子場論中已經存在的對偶關系作為登陸點,達到取其精華、去其糟粕的目的。我們看到,量子細胞場論以比量子場論簡單得多的推理便獲得了相同的經過實驗檢驗的結論,並附帶著解決了量子場論中許多由來已久的困惑。從這個角度來說,量子細胞場論也可以稱為簡化量子場論,或者稱為數學家會喜歡的對偶場論,當然我們最喜歡的還是帶點物理味道的量子細胞場論這個稱呼。
自對偶性與彭羅斯的扭量理論有關,也與共形不變性有關;可以證明在任意的偶數維中只存在場強為自對偶的自由共形理論;在任意奇數維中自由共形理論只存在標量與旋量。這個定理說明了在量子細胞場論中為什麽包括引力子在內的規範玻色子的測地線遵守的是龐加萊雙曲幾何模型,當且僅當在這種情況下規範場強才是自對偶的並且是共形不變的,這條定理可以作為量子細胞場論的一條基本定理。
人類關於對偶性的認識最早可以追溯到亞裏士多德的認識論;按照Aristotle的觀點,每種對象都有對偶性質。在數學中也存在大量的對偶格,這裏牽涉到零化子(Annihilator);存在一個空間與其對偶空間之間的雙射,這種雙射被稱為Galois對偶性;這種Galois對偶性在數學中到處都有,對於場論、算子理論、代數幾何及動態系統都非常有用。
共形不變性和標度不變性
共形不變性
自對偶性與彭羅斯的扭量理論有關,也與共形不變性有關;可以證明在任意的偶數維中只存在場強為自對偶的自由共形理論;在任意奇數維中自由共形理論只存在標量與旋量。這個定理說明了在量子細胞場論中為什麽包括引力子在內的規範玻色子的測地線遵守的是龐加萊雙曲幾何模型,當且僅當在這種情況下規範場強才是自對偶的並且是共形不變的,這條定理可以作為量子細胞場論的一條基本定理。
人類關於對偶性的認識最早可以追溯到亞裏士多德的認識論;按照Aristotle的觀點,每種對象都有對偶性質。在數學中也存在大量的對偶格,這裏牽涉到零化子(Annihilator);存在一個空間與其對偶空間之間的雙射,這種雙射被稱為Galois對偶性;這種Galois對偶性在數學中到處都有,對於場論、算子理論、代數幾何及動態系統都非常有用。
共形不變性和標度不變性
由於量子細胞場論中所有傳遞相互作用的規範場都滿足共形不變的條件,所以我們需要對共形變換的性質多些了解,而且共有不變性和標度不變性分別與重正化群和重正化有密切聯系。碰巧許多標度不變的理論在共形群作用下也是不變的;共形不變性隱含了標度不變性,因為一個無窮小共形變換和一個無窮小平移變換的對易子包含一個標度變換。反過來就不一定正確了;只有當被考慮的理論中存在一個對稱無跡的守恒能量-動量張量時,標度不變性才隱含了共形不變性;可以證明所有自旋≤1的可重正化場論中都存在這樣一個能量-動量張量。在有偶數維時間軸的四維時空中,洛侖茲群可以分解為兩個SU(2)或兩個特殊線性群SL(2)的乘積;對於4維Yang-Mills場而言,這使得自對偶性的表述非常簡單,可以利用明顯保持共形不變性的表達式;可以利用額外的維使得共形不變性明顯,然後利用投射光錐坐標定義協變導數。
如果在一個經典的作用量中所有有量綱的常數都不存在,我們預期這個理論是標度不變的;對於一個有質量的理論,在小距離上也可能發生這種情況。期望在大動量下質量可被忽略時,理論變為標度不變的事實上是太簡化了。漸近行為是由相應的無質量理論給出的。重正化迫使我們選取一任意能量標度,這個能量標度破壞了量綱分析,正是這種任意性事實上挽救了我們,標度的改變可以歸結為耦合常數的修改。相應的流由類似於β系數的函數所主宰,因此重正化群變換取代了簡單的量綱分析。
如果組態變換被重新標度,也可以考慮這種變換在有質量的理論中的效應,因而得到反映標度不變性破壞的Ward恒等式。在這個意義上講,這裏的分析與純粹的量綱分析是不同的。因為我們這裏考慮的是動力學變量(場)變換的效應,而不是有量綱的參數(例如質量)的變換的效應。如果我們打算這樣做,就會把兩種不同的物理情況聯系起來。
如果在一個經典的作用量中所有有量綱的常數都不存在,我們預期這個理論是標度不變的;對於一個有質量的理論,在小距離上也可能發生這種情況。期望在大動量下質量可被忽略時,理論變為標度不變的事實上是太簡化了。漸近行為是由相應的無質量理論給出的。重正化迫使我們選取一任意能量標度,這個能量標度破壞了量綱分析,正是這種任意性事實上挽救了我們,標度的改變可以歸結為耦合常數的修改。相應的流由類似於β系數的函數所主宰,因此重正化群變換取代了簡單的量綱分析。
如果組態變換被重新標度,也可以考慮這種變換在有質量的理論中的效應,因而得到反映標度不變性破壞的Ward恒等式。在這個意義上講,這裏的分析與純粹的量綱分析是不同的。因為我們這裏考慮的是動力學變量(場)變換的效應,而不是有量綱的參數(例如質量)的變換的效應。如果我們打算這樣做,就會把兩種不同的物理情況聯系起來。
共形不變性
可以證明共形不變性是標度不變性的一個結果。共形群定義為保持角度不變的變換的集合,這將轉到Minkowski空間,在此空間可以處理雙曲形和圓形的角,將關於任意一點的反演附加到龐加萊變換上就得到這個群,我們考慮一個具有(2,4)度規的六維空間;為了使這個定義有意義,通常的歐氏四維空間必須被在無窮遠的圓錐曲線所封閉。這可以通過下面的方法來實現,用超平面切割圓錐曲線,並且把所得的單葉雙曲面從高維空間球極投影到四維歐氏空間即可。可以定義雙曲度量,也稱為龐加萊度量;我們可以通過線性變換求區域內任意兩點間的雙曲距離,雙曲距離在解析變換下是收縮的。四葉贗正交群O(2,4)的作用在Minkowski空間上表現為共形變換;特別是膨脹對應於雙曲轉動。
在場論中刻畫共形變換的最簡單方法是將其作為一個局域標度變換。當然,只有當它具有全局標度不變性時,作用量才是在局域標度變換下保持不變的,這時引力耦合常數必須是無量綱的;這時我們可以在引力作用量中用共形拉氏量代替龐加萊不變的拉氏量,就像是在Yang-Mills理論中一樣。如果引力耦合理論在這個局域標度變換下不變,則當引力去耦合後理論是共形不變的,結合了坐標變換、局域標度變換和洛侖茲變換並保持正交標架的變換恰好是一個共形變換。考慮有一個共形不變的作用量但沒包括引力的場論,標度不變對稱性的自發破缺產生出一個Goldstone玻色子,即伸縮子。伸縮子的作用類似於Higgs場:如果伸縮子與共形引力耦合,Higgs場將共形引力約化為愛因斯坦引力。
引力的Einstein-Hilbert作用量來自於導數中僅有的二階標量,即Ricci標量。與Yang-Mills場相比,這個作用量是有量綱的,但量綱可以通過重新定義標架場吸收到所謂“真空”當中,這樣就變得無量綱的。從這個意義上講,引力是一種共形不變性“自發性破缺”而產生的力,坐標變換包含了共形變換,但通過引入一個長度標度這個不變性被真空破缺了;重要的是,在量子細胞引力論中,由於引力服從橢圓幾何是一種保持一對對合點不變的力,這種量子場論中所謂的真空也不必存在了。對於Dirac場來講,對偶性與手征性是同一回事;這種連續的手征和對偶的對稱性可以擴展到四維時空的任何無質量場的自由場方程中,它們區別這種場的波動的兩種極化方式。它們與共形不變性密切相關:在高維中,不是所有的無質量理論都是共形的,只有具有對偶性的場才是共形的。
在場論中刻畫共形變換的最簡單方法是將其作為一個局域標度變換。當然,只有當它具有全局標度不變性時,作用量才是在局域標度變換下保持不變的,這時引力耦合常數必須是無量綱的;這時我們可以在引力作用量中用共形拉氏量代替龐加萊不變的拉氏量,就像是在Yang-Mills理論中一樣。如果引力耦合理論在這個局域標度變換下不變,則當引力去耦合後理論是共形不變的,結合了坐標變換、局域標度變換和洛侖茲變換並保持正交標架的變換恰好是一個共形變換。考慮有一個共形不變的作用量但沒包括引力的場論,標度不變對稱性的自發破缺產生出一個Goldstone玻色子,即伸縮子。伸縮子的作用類似於Higgs場:如果伸縮子與共形引力耦合,Higgs場將共形引力約化為愛因斯坦引力。
引力的Einstein-Hilbert作用量來自於導數中僅有的二階標量,即Ricci標量。與Yang-Mills場相比,這個作用量是有量綱的,但量綱可以通過重新定義標架場吸收到所謂“真空”當中,這樣就變得無量綱的。從這個意義上講,引力是一種共形不變性“自發性破缺”而產生的力,坐標變換包含了共形變換,但通過引入一個長度標度這個不變性被真空破缺了;重要的是,在量子細胞引力論中,由於引力服從橢圓幾何是一種保持一對對合點不變的力,這種量子場論中所謂的真空也不必存在了。對於Dirac場來講,對偶性與手征性是同一回事;這種連續的手征和對偶的對稱性可以擴展到四維時空的任何無質量場的自由場方程中,它們區別這種場的波動的兩種極化方式。它們與共形不變性密切相關:在高維中,不是所有的無質量理論都是共形的,只有具有對偶性的場才是共形的。
對偶格(Dual Lattice)
考慮對偶的雙射Ann(A∨B)=(Ann A)∪(Ann B);Ann(A∪B)=(Ann A)∨(Ann B)。這裏Ann是零化子,我們可以將"∨"解釋為幾率幅的相加,將張量和∪解釋為真正並行的加法。這種稱呼源自於計算機科學,在計算機邏輯體系中存在兩種並發的系統:一種是交叉語義的系統,一種是真正並發的系統,在真正並發的系統中加法就稱為張量和。與質量有關的加法當然是真正並發的系統;而幾率幅的加法最終要與相位因子聯系在一起,這是量子力學的基本假設。
要將質量與量子力學的基本假設真正統一到一起,還需要另外兩個算符“<”和“>”;我們無法控制細胞吃進食物(它的對偶空間)而變得越來越胖,我們也無法控制產生算符在核子內任意地復制誇克;但對於量子細胞我們可以計算它的排序,在核子內每增加一個虛誇克序值加一,這樣就可以將復制算符產生的序列變為偏序集,這時對偶細胞可以發揮作用,相應地將序值減一,這兩個算符對應的是一對顛倒順序的(order reversing)雙射。有了這兩個顛倒順序算符,我們就可以將兩個偏序集合成為一個統一的系統。
算符“<”和“>”將一個空間中的元素映射到對偶空間裏,這兩個算符稱為Galois聯絡;如果有一個結論是正確的,而你同時交換空間和對偶空間的位置以及“<”和“>”的位置,導出的結論同樣也是正確的。重要的是,復合算符<>和><是代數封閉算符,如果作用於核子空間這兩個合成算符是同位旋對稱性產生的根源。假如我們只是需要一個費米子內相位因子與質量的對偶性,那麽“<”和“>”算符就沒有差別,從Galois聯絡的觀點來看,這樣的關系是一個完備格上的自對偶性。
要將質量與量子力學的基本假設真正統一到一起,還需要另外兩個算符“<”和“>”;我們無法控制細胞吃進食物(它的對偶空間)而變得越來越胖,我們也無法控制產生算符在核子內任意地復制誇克;但對於量子細胞我們可以計算它的排序,在核子內每增加一個虛誇克序值加一,這樣就可以將復制算符產生的序列變為偏序集,這時對偶細胞可以發揮作用,相應地將序值減一,這兩個算符對應的是一對顛倒順序的(order reversing)雙射。有了這兩個顛倒順序算符,我們就可以將兩個偏序集合成為一個統一的系統。
算符“<”和“>”將一個空間中的元素映射到對偶空間裏,這兩個算符稱為Galois聯絡;如果有一個結論是正確的,而你同時交換空間和對偶空間的位置以及“<”和“>”的位置,導出的結論同樣也是正確的。重要的是,復合算符<>和><是代數封閉算符,如果作用於核子空間這兩個合成算符是同位旋對稱性產生的根源。假如我們只是需要一個費米子內相位因子與質量的對偶性,那麽“<”和“>”算符就沒有差別,從Galois聯絡的觀點來看,這樣的關系是一個完備格上的自對偶性。
基於聯絡還是基於規範
從量子場論的重正化觀點來看,無質量Yang-Mills場的庫侖規範或哈密頓規範,有質量場的幺正規範是不方便的;在前兩種情況下,沒有明顯的相對論不變性,而在後一情況下不存在明顯的可重正性;在這一意義上更加方便得多的是明顯協變的規範,例如洛侖茲規範;然而,在洛侖茲規範中,不能構造哈密頓理論體系,因而S矩陣的幺正性不明顯。量子細胞場論是基於聯絡的,聯絡中既包含了洛侖茲規範又包含了庫侖規範因而滿足幺正性,這對於重正化非常有利。
從量子場論算符形式的觀點來看,洛侖茲規範中的S矩陣作用在一個既包含物理的態又包含非物理的態,包含縱光子和時間光子、標量費米子、Goldstone玻色子的巨空間中;一般說來,量子場論只有在這一空間中才是幺正的,而在這一空間中度規不定。量子細胞場論的聯絡包含了所有這些分量,采用不需要不定度規的純幾何的細胞量子化方法,帶來的唯一副作用是光子在內部空間的傳播速度是πc/2,但這與量子場論遇到的麻煩相比可以忽略不計,況且這一副作用未必是壞事情。
在物理子空間中,S矩陣的幺正性是相對性原理的結論;按照這一原理,所有可觀測量都不依賴於實際選擇的規範條件。在量子場論裏我們可以證明,S矩陣系數函數在庫侖規範中的一個明顯幺正的泛函,可以恒等地轉變為洛侖茲規範中的泛函,然而論證是在沒有重正化的前提下進行的因而帶有形式的性質;在量子細胞場論中,矢量分量與標量分量天生就是對偶的。相對性原理用於量子場論的重正化理論不是件容易的事,量子場論中先重正化,然而還要證明重正化的拉氏量是規範不變的;我們看到這一手續對於量子細胞場論來說是多余的。
從量子場論算符形式的觀點來看,洛侖茲規範中的S矩陣作用在一個既包含物理的態又包含非物理的態,包含縱光子和時間光子、標量費米子、Goldstone玻色子的巨空間中;一般說來,量子場論只有在這一空間中才是幺正的,而在這一空間中度規不定。量子細胞場論的聯絡包含了所有這些分量,采用不需要不定度規的純幾何的細胞量子化方法,帶來的唯一副作用是光子在內部空間的傳播速度是πc/2,但這與量子場論遇到的麻煩相比可以忽略不計,況且這一副作用未必是壞事情。
在物理子空間中,S矩陣的幺正性是相對性原理的結論;按照這一原理,所有可觀測量都不依賴於實際選擇的規範條件。在量子場論裏我們可以證明,S矩陣系數函數在庫侖規範中的一個明顯幺正的泛函,可以恒等地轉變為洛侖茲規範中的泛函,然而論證是在沒有重正化的前提下進行的因而帶有形式的性質;在量子細胞場論中,矢量分量與標量分量天生就是對偶的。相對性原理用於量子場論的重正化理論不是件容易的事,量子場論中先重正化,然而還要證明重正化的拉氏量是規範不變的;我們看到這一手續對於量子細胞場論來說是多余的。
規範對稱性
在量子細胞場論中有兩種類型的規範變換:第一種就是量子場論意義上的規範變換;第二種是由對合關系生成的規範,在量子細胞場論中有各種層次下的對合關系,在電磁場中正電荷與負電荷對合,在弱相互作用中電子與中微子對合,在引力相互作用中兩個相互作用的物體構成對合關系,由對合關系生成的群是相似變換群,正是Weyl提出規範場論時最初考慮的那個群,顯然已經被量子場論束之高閣多年並且有可能隨時被會當垃圾扔掉。我們很想將兩種規範變換分別稱為第一類規範變換和第二類規範變換,但這種分類法已經被量子場論用掉了,在量子場論中這兩個名詞分別代表整體規範變換和局域規範變換;不過我們可以按照橢圓幾何的分類方法將兩類變換分別稱為單重規範變換和雙重規範變換,或者將量子場論中的規範統稱為楊(Yang)規範,將量子細胞場論中的雙重規範統稱為Weyl規範。
Weyl規範的作用並不亞於楊規範的作用,只是被量子場論忽視了,聯系上重正化就可以看得很明白。僅當實施一個標度變換後,一個著衣粒子與一個裸粒子都遵守同樣的規律時,這個理論才是可重正化的;舉例來說當實施了標度變換後,電磁場仍服從同樣的一些方程。利用重正化常數的定義,可以重新標度傳播子和頂角,以及電荷。由這個重新標度所定義的重正化常數可以反過來與傳播子和頂角相聯系。這把我們帶到問題的關鍵之處,即證明:至重整後的電荷的每一階,這些量和方程都是有限的,所以依賴於截斷的項在重新標度定律中都被吸收了。重正化的思想是:重新標度傳播子和頂角函數,以使在質殼附近,以及在頂角情形下對於零動量傳遞,這些量趨於自由粒子的相應的量。
將重正化思想應用於廣義相對論,似乎要大難臨頭了,重正化要求標度不變性,引力恰恰是由於標度不變性的破缺而產生的一種力;用重正化的辦法修改廣義相對論,廣義相對論變得越修就越奇怪,一個無窮大會引出更多的無窮大,在重正化方面廣義相對論簡直可以用“臭名昭著”這四個字來形容。我們發現,這些理論上的偏差完全是由於量子場論對標度不變性、Weyl規範和廣義相對論的本質以及它們之間的相互關系沒有完全理解造成的。
Weyl規範的作用並不亞於楊規範的作用,只是被量子場論忽視了,聯系上重正化就可以看得很明白。僅當實施一個標度變換後,一個著衣粒子與一個裸粒子都遵守同樣的規律時,這個理論才是可重正化的;舉例來說當實施了標度變換後,電磁場仍服從同樣的一些方程。利用重正化常數的定義,可以重新標度傳播子和頂角,以及電荷。由這個重新標度所定義的重正化常數可以反過來與傳播子和頂角相聯系。這把我們帶到問題的關鍵之處,即證明:至重整後的電荷的每一階,這些量和方程都是有限的,所以依賴於截斷的項在重新標度定律中都被吸收了。重正化的思想是:重新標度傳播子和頂角函數,以使在質殼附近,以及在頂角情形下對於零動量傳遞,這些量趨於自由粒子的相應的量。
將重正化思想應用於廣義相對論,似乎要大難臨頭了,重正化要求標度不變性,引力恰恰是由於標度不變性的破缺而產生的一種力;用重正化的辦法修改廣義相對論,廣義相對論變得越修就越奇怪,一個無窮大會引出更多的無窮大,在重正化方面廣義相對論簡直可以用“臭名昭著”這四個字來形容。我們發現,這些理論上的偏差完全是由於量子場論對標度不變性、Weyl規範和廣義相對論的本質以及它們之間的相互關系沒有完全理解造成的。
重正化
量子場論沒有說清楚標度不變性和共形不變性之間的內在聯系,因為這兩種不變性之間不是一一對應的關系。在量子細胞場論中,標度不變性是在相似變換群和共形變換群共同作用下產生的;相似變換群與共形變換群在局部是對偶的,存在一一對應的關系。相似變換群是仿射群的子群,相似變換群叢上可以定義仿射聯絡,即Levi-Civita聯絡並進而定義恒為正的曲率,我們稱之為愛因斯坦場強張量,可以自然地導出潮汐引力相互作用。由共形變換群也可以定義與愛因斯坦場強張量對偶的曲率,我們稱之為龐加萊場強張量,這個場強張量引出的是斥力。
量子細胞場論中的對合點還有另外一層的意思,我們知道要從射影幾何的中心射影變換到仿射幾何的平行射影,需要添加一條無窮遠直線,在龐加萊模型中,無窮遠直線就是規範玻色子的測地線,現在測地線與無窮遠的邊界有兩個交點,正是這兩個對合點,這符合雙曲幾何的性質:雙曲幾何的二次絕對形與無窮遠直線有兩個交點。
量子場論的重正化方法主要考慮的是楊規範的作用,Weyl規範只是作為輔助變量引入的,對於電磁相互作用和弱相互作用而言,這種方法無可厚非,這兩種場都符合標度不變性的要求,截斷動量不起實質性作用。在強相互作用中,楊規範還是起主導作用,但是能量標度已經破壞了量綱分析,能量標度與耦合常數之間存在一種對數關系。在引力相互作用中,耦合強度更是與慣性質量成線性關系,引力完全是由Weyl規範直接造成的。
這裏有一條好消息。如果你認為引力也存在真空極化作用,那麽裸荷與抵消項兩者精確地相等,這同引力不會引起偶極輻射的性質有關,量子場論中那令人煩惱的無窮大沒有出現,無窮大不過是量子場論的幻覺,地球還照樣地轉,我們又可以高枕無憂了。情況與量子場論中恰好相反,楊規範在量子細胞引力中被精確地抵消了,只剩下Weyl規範起作用,這也可以回答為什麽引力相互作用的耦合強度是如此的弱,如果我們計算兩個質子之間的萬有引力與靜電力的比值,這兩種力的作用強度之間要相差37個數量級,因為一階引力作用被完全抵消了,只存在二階引力效應,愛因斯坦場強張量是一種二階場強張量。
這讓我們想起了核力,由於誇克禁閉的作用,楊規範產生的力只對核子之間的作用力產生間接影響,誇克與反誇克組成對合點,介子是由一對誇克與反誇克組成的無色粒子,可以認為核力主要是由於Weyl規範造成的,從這個意義上說,引力更像核力而不像強作用力。那麽核力的作用強度是否也與慣性質量成正比呢,由於核力是短程力,引力是長程力,它們之間似乎沒有可比性;但是電磁相互作用是長程力而弱相互作用是短程力,兩種相互作用竟然是同一種力;關於這個問題的答案我們至今仍然是一頭霧水。
量子細胞場論中的對合點還有另外一層的意思,我們知道要從射影幾何的中心射影變換到仿射幾何的平行射影,需要添加一條無窮遠直線,在龐加萊模型中,無窮遠直線就是規範玻色子的測地線,現在測地線與無窮遠的邊界有兩個交點,正是這兩個對合點,這符合雙曲幾何的性質:雙曲幾何的二次絕對形與無窮遠直線有兩個交點。
量子場論的重正化方法主要考慮的是楊規範的作用,Weyl規範只是作為輔助變量引入的,對於電磁相互作用和弱相互作用而言,這種方法無可厚非,這兩種場都符合標度不變性的要求,截斷動量不起實質性作用。在強相互作用中,楊規範還是起主導作用,但是能量標度已經破壞了量綱分析,能量標度與耦合常數之間存在一種對數關系。在引力相互作用中,耦合強度更是與慣性質量成線性關系,引力完全是由Weyl規範直接造成的。
這裏有一條好消息。如果你認為引力也存在真空極化作用,那麽裸荷與抵消項兩者精確地相等,這同引力不會引起偶極輻射的性質有關,量子場論中那令人煩惱的無窮大沒有出現,無窮大不過是量子場論的幻覺,地球還照樣地轉,我們又可以高枕無憂了。情況與量子場論中恰好相反,楊規範在量子細胞引力中被精確地抵消了,只剩下Weyl規範起作用,這也可以回答為什麽引力相互作用的耦合強度是如此的弱,如果我們計算兩個質子之間的萬有引力與靜電力的比值,這兩種力的作用強度之間要相差37個數量級,因為一階引力作用被完全抵消了,只存在二階引力效應,愛因斯坦場強張量是一種二階場強張量。
這讓我們想起了核力,由於誇克禁閉的作用,楊規範產生的力只對核子之間的作用力產生間接影響,誇克與反誇克組成對合點,介子是由一對誇克與反誇克組成的無色粒子,可以認為核力主要是由於Weyl規範造成的,從這個意義上說,引力更像核力而不像強作用力。那麽核力的作用強度是否也與慣性質量成正比呢,由於核力是短程力,引力是長程力,它們之間似乎沒有可比性;但是電磁相互作用是長程力而弱相互作用是短程力,兩種相互作用竟然是同一種力;關於這個問題的答案我們至今仍然是一頭霧水。
弦論中的超對稱性與對偶性
從校友李渺那裏抄來一段文字,可以作為量子細胞場論正確性的間接證明,或許我們的許多想法對弦論也有啟發。我們的重點是討論量子細胞場論與弦論的聯系,以及量子細胞場論如何使得弦論中幻想的部分變得比較實際了,對弦論更詳細的描述請參見李渺的原著。
“弦論起源於一九六零年代的粒子物理,當時的強相互作用一連串實驗表明存在無窮多個強子,質量與自旋越來越大越來越高。這些粒子絕大多數是不穩定粒子,所以叫做共振態。當無窮多的粒子參與相互作用時,粒子與粒子散射振幅滿足一種奇怪的性質,叫做對偶性。1968年,一個在麻省理工學院工作的意大利物理學家威尼采亞諾(Gabriele Veneziano) 翻了翻數學手冊,發現一個簡單的函數滿足對偶性,這就是著名的Veneziano公式。
所謂Seiberg-威頓理論將超對稱和對偶性結合起來,一下子得到自有四維量子場論以來最為動人的結果。這件事發生在1994年夏天。這是一個自第一次弦論革命以來近十年中的重大突破;這個突破的感染力慢慢擴散開來,大多數人的反應是從不相信到半信半疑,直至身不由己地卷入隨之而來的量子場論和弦論長達4年的革命。很多人記得從94年夏到95年春,Los Alamos hep-th專門張貼高能物理理論文的電子“檔案館”多了很多推廣和應用Seiberg-威頓理論的文章,平淡冷落的理論界開始復蘇。Seiberg和威頓後來以此項工作獲得1998 年度美國物理學會的海因曼獎。不同超對稱規範理論之間的對偶性,後來被稱為Seiberg對偶,也是相當重要的工作。
量子引力本身必定是有簡單定義的理論,換言之,量子引力是一個更大的,可重正的甚至是有限的理論的一部份。這個理論不太可能是愛因斯坦理論的簡單量子化,因為我們已知道愛因斯坦理論不可能被簡單地量子化。這就迫使我們尋找一個更大的,至少是可重正的理論。我們將被歷史地,在某種程度上也是邏輯地帶到超對稱。有了超對稱,與新能標的平方成正比的項不再存在,所以80年代初很多人研究超對稱大統一理論。這是超弦集團之外的唯象粒子物理學家相信超對稱存在的主要原因之一。超對稱的生成元越多,無限大的抵消就越成功,但人們為此付出的代價是模型越來越不現實。當超對稱元的個數超過16時,我們不得不引進自旋為2的粒子以構造超對稱多重態,這樣就引進了引力。”
“弦論起源於一九六零年代的粒子物理,當時的強相互作用一連串實驗表明存在無窮多個強子,質量與自旋越來越大越來越高。這些粒子絕大多數是不穩定粒子,所以叫做共振態。當無窮多的粒子參與相互作用時,粒子與粒子散射振幅滿足一種奇怪的性質,叫做對偶性。1968年,一個在麻省理工學院工作的意大利物理學家威尼采亞諾(Gabriele Veneziano) 翻了翻數學手冊,發現一個簡單的函數滿足對偶性,這就是著名的Veneziano公式。
所謂Seiberg-威頓理論將超對稱和對偶性結合起來,一下子得到自有四維量子場論以來最為動人的結果。這件事發生在1994年夏天。這是一個自第一次弦論革命以來近十年中的重大突破;這個突破的感染力慢慢擴散開來,大多數人的反應是從不相信到半信半疑,直至身不由己地卷入隨之而來的量子場論和弦論長達4年的革命。很多人記得從94年夏到95年春,Los Alamos hep-th專門張貼高能物理理論文的電子“檔案館”多了很多推廣和應用Seiberg-威頓理論的文章,平淡冷落的理論界開始復蘇。Seiberg和威頓後來以此項工作獲得1998 年度美國物理學會的海因曼獎。不同超對稱規範理論之間的對偶性,後來被稱為Seiberg對偶,也是相當重要的工作。
量子引力本身必定是有簡單定義的理論,換言之,量子引力是一個更大的,可重正的甚至是有限的理論的一部份。這個理論不太可能是愛因斯坦理論的簡單量子化,因為我們已知道愛因斯坦理論不可能被簡單地量子化。這就迫使我們尋找一個更大的,至少是可重正的理論。我們將被歷史地,在某種程度上也是邏輯地帶到超對稱。有了超對稱,與新能標的平方成正比的項不再存在,所以80年代初很多人研究超對稱大統一理論。這是超弦集團之外的唯象粒子物理學家相信超對稱存在的主要原因之一。超對稱的生成元越多,無限大的抵消就越成功,但人們為此付出的代價是模型越來越不現實。當超對稱元的個數超過16時,我們不得不引進自旋為2的粒子以構造超對稱多重態,這樣就引進了引力。”
Weyl規範復活了!
弦論中的超對稱性完全是假設,沒有獲得任何物理實驗的支持。量子細胞場論中存在兩種類型的“超對稱性”:一種類似於超對稱場論中費米子與玻色子之間的對稱性,是無窮遠點或元素與普通點或元素之間的對稱性,這種對稱性是射影空間的完備性的自然推論,正確性是無庸置疑的;另一種是由對合關系導出的,介子中的正、反誇克構成對合關系,而誇克禁閉現象已獲得大量實驗的支持,所以量子細胞場論中的這種超對稱性也一定是正確的。
現在我們可以明白為什麽Weyl規範成了被量子場論遺忘的角落,翻遍規範場論的書籍已很難找到規範場論這個“祖宗”的痕跡,U(1)規範是自對偶的,最初的Weyl規範不是對偶的,自然不會獲得“造物主”的支持,只能讓位於U(1)規範。量子細胞場論中,相似變換群是對合關系生成的,成了一種長程的規範,這也是量子細胞場論的規範與量子場論規範的一個重要區別:量子場論的規範都是發生於一點上的,例如費米子與玻色了的超對稱性;相互作用發生於一點上自然會帶出討厭的無窮大。並且我們也導出了長程的Weyl規範的一個重要證據,將滿足局域規範對稱性的色力提升為整體對稱性便自然得到了核力,這裏我們用提升這個詞是恰當的,因為在數學上也是這麽稱呼的。重要的是,相似變換群導出一個伸的變化,與共形變換群生成的縮變化是對偶的,有了對偶性的Weyl規範自然會獲得“造物主”的支持。
現在我們可以明白為什麽Weyl規範成了被量子場論遺忘的角落,翻遍規範場論的書籍已很難找到規範場論這個“祖宗”的痕跡,U(1)規範是自對偶的,最初的Weyl規範不是對偶的,自然不會獲得“造物主”的支持,只能讓位於U(1)規範。量子細胞場論中,相似變換群是對合關系生成的,成了一種長程的規範,這也是量子細胞場論的規範與量子場論規範的一個重要區別:量子場論的規範都是發生於一點上的,例如費米子與玻色了的超對稱性;相互作用發生於一點上自然會帶出討厭的無窮大。並且我們也導出了長程的Weyl規範的一個重要證據,將滿足局域規範對稱性的色力提升為整體對稱性便自然得到了核力,這裏我們用提升這個詞是恰當的,因為在數學上也是這麽稱呼的。重要的是,相似變換群導出一個伸的變化,與共形變換群生成的縮變化是對偶的,有了對偶性的Weyl規範自然會獲得“造物主”的支持。
射影變換與相似變換
對合對應(Involution)與長程Weyl規範
可以預料相似變換群等概念是統一場論的基礎,有必要了解一下。射影群的一個子群是一族仿射變換,這個子群定義如下:設在射影平面上固定任一無窮遠直線,無窮遠直線上的點稱為理想點或無窮遠點。任何度量幾何群,除了變換行列式的值必須是+1或-1外,和仿射群相同。第一個度量幾何是Euclid幾何,要定義這種幾何群,我們從無窮遠直線開始,並假設在無窮遠直線上有固定的對合變換;我們要求這個對合變換沒有實的二重點,而以無窮遠處的虛圓點作為二重點。現考慮所有那樣的射影變換,它們不僅使無窮遠直線不變而且把對合的任何點變到對合的對應點,此即蘊含每個虛圓點變到自身。Euclid群的這些變換,不變的是長度、角的大小,任何圖形的大小與形狀。用這種分類法的術語來講,Euclid幾何就是在這類變換下的一組不變量;這類變換是:旋轉、平移和反射。
要得到關於相似形的不變量,我們引進仿射群的子群,名為拋物度量群;這個群定義為一族射影變換,它使得無窮遠直線上的對合不變,這就意味著每一對相應的點變到相應的另一對點;Euclid幾何是拋物度量幾何的子幾何。要刻劃雙曲度量幾何,我們再回到射影幾何,在射影平面上考慮一個任意的、實的、非退化的絕對形;射影的子群使這個二次曲線不變的叫做雙曲度量群。即使二重橢圓幾何也能包括在這種變換觀點之內,但我們必須從三維變換群出發來刻劃二維的這種度量幾何。
變換下不變性的物理問題,或者物理定律的表達方式不依賴於坐標系的問題,在人們註意到Maxwell方程經典仿射幾何的四維子群,即Lorentz群變換下的不變性之後,在物理思想中都變成重要;這種思想路線引向狹義相對論。
要得到關於相似形的不變量,我們引進仿射群的子群,名為拋物度量群;這個群定義為一族射影變換,它使得無窮遠直線上的對合不變,這就意味著每一對相應的點變到相應的另一對點;Euclid幾何是拋物度量幾何的子幾何。要刻劃雙曲度量幾何,我們再回到射影幾何,在射影平面上考慮一個任意的、實的、非退化的絕對形;射影的子群使這個二次曲線不變的叫做雙曲度量群。即使二重橢圓幾何也能包括在這種變換觀點之內,但我們必須從三維變換群出發來刻劃二維的這種度量幾何。
變換下不變性的物理問題,或者物理定律的表達方式不依賴於坐標系的問題,在人們註意到Maxwell方程經典仿射幾何的四維子群,即Lorentz群變換下的不變性之後,在物理思想中都變成重要;這種思想路線引向狹義相對論。
對合對應(Involution)與長程Weyl規範
廣義相對論的局部慣性系是針對時空的每一點定義的,雖然通過仿射聯絡可以導出彎曲的定義,卻使得廣義相對論在重正化的考量方面“惡名遠播”。事實上通過對合關系也可以使時空彎曲起來,量子細胞場論中的每一點都是一個射影空間的纖維,但單獨一個纖維上的對合關系只能導出相似變換群,沒有使時空彎曲起來;但有了纖維叢以後,由於在每一個纖維上場都是自對偶的,也就是自配極的,沿著纖維叢不同纖維之間移動,就會生成一個自配極的二級曲線,我們認出這個自配極的二極曲線可以是橢圓曲線或者雙曲的,相應地給出引力或斥力。所以長程對合關系生成的長程Weyl規範可以使時空彎曲起來,因此我們對involution這個概念進一步了解是有意義的。
對合對應是具有公共底的兩上一維基本形的射影對應的一種重要的特殊情形。射影對應因兩個自身對應元素的虛實與異同分為三種情況:有兩上實的不同自身對應元素的是雙曲射影對應;有兩個實的相同的自身對應元素的是拋物射影對應;有兩個虛的自身對應元素的是橢圓射影對應。雙曲型射影對應的兩個二重元素與每對對應元素組成的交比都相等;由於在龐加萊雙曲幾何模型中,距離是用交比來定義的,這就證明了我們的馬德西特時空模型是合理的。
二次曲線上點列的射影對應的二重點是透視軸與二次曲線的交點,反之亦然,利用它作二重點時,當然只要作透視軸與曲線的交點就行了。關於實交點的個數問題,有三種可能的射影,就是:有一個交點的稱為拋物射影對應,有二個交點的稱為雙曲射影對應,無實交點的而有二個虛交點的稱為橢圓射影對應。具有公共底的二級線束之間的射影對應,是二次點列情形的對偶,特別是對應的二重直線,是二級線束裏通過中心的直線。關於二重直線也有三種可能情形:有兩條二重直線的是雙曲型的,有一條二重直線的是拋物型的,無二重直線是橢圓型的。
對合對應是具有公共底的兩上一維基本形的射影對應的一種重要的特殊情形。射影對應因兩個自身對應元素的虛實與異同分為三種情況:有兩上實的不同自身對應元素的是雙曲射影對應;有兩個實的相同的自身對應元素的是拋物射影對應;有兩個虛的自身對應元素的是橢圓射影對應。雙曲型射影對應的兩個二重元素與每對對應元素組成的交比都相等;由於在龐加萊雙曲幾何模型中,距離是用交比來定義的,這就證明了我們的馬德西特時空模型是合理的。
二次曲線上點列的射影對應的二重點是透視軸與二次曲線的交點,反之亦然,利用它作二重點時,當然只要作透視軸與曲線的交點就行了。關於實交點的個數問題,有三種可能的射影,就是:有一個交點的稱為拋物射影對應,有二個交點的稱為雙曲射影對應,無實交點的而有二個虛交點的稱為橢圓射影對應。具有公共底的二級線束之間的射影對應,是二次點列情形的對偶,特別是對應的二重直線,是二級線束裏通過中心的直線。關於二重直線也有三種可能情形:有兩條二重直線的是雙曲型的,有一條二重直線的是拋物型的,無二重直線是橢圓型的。
配極對應
兩個點偶,如果互相不點離,它們就決定一個雙曲對合,也就是說,它們所決定的對合有兩個雙重點;而如果它們互相分離,就決定一個橢圓對合,也就是說,這個對合沒有實的雙重點,只有兩個虛的雙重點。配極對應是一種點線對應,關於配極對應的對合性質,也是由極點、極線性質產生的,此外,雙因為關於一個二次曲線的極點與極線都是這個二次曲線所在平面上的元素,所以配極對就是同一個平面上兩個場之間的異素對應。
點線對應當中,對合的點線對應就是配極對應,所以也可將配極對應稱為對合的點線對應,而點線對應可以使一個圖形的射影性質轉變為其對偶圖形的相應性質。由射影變換的全體以及點線變換的全體合並而成的群稱為廣義射影變換群,利用它可以研究點線不分的射影幾何學。
強相互作用中的對偶性假設
點線對應當中,對合的點線對應就是配極對應,所以也可將配極對應稱為對合的點線對應,而點線對應可以使一個圖形的射影性質轉變為其對偶圖形的相應性質。由射影變換的全體以及點線變換的全體合並而成的群稱為廣義射影變換群,利用它可以研究點線不分的射影幾何學。
強相互作用中的對偶性假設
在傳統強相互作用理論和核相互作用中,我們就有了兩幅圖景。在其中的一幅中,核力是基本的,強力的場線是一種近似描述;而在另一幅圖景中,強力的場線是基本的,而核子是一種從中導出的實體。在量子細胞場論中,核子圖景和強作用力圖景僅僅是看待某一相同事物的兩種不同方式而已,在量子細胞場論中,這一對偶性假設跟量子理論中的波粒二象性是同一回事。這一假設對量子引力也起著非常重要的作用,我們做的就是用自對偶細胞來代替粒子,這樣幾個困擾物理學很長時間的問題就可以被解決了。
對偶性假設告訴我們,兩個看起來不同的現象其實只是描述同一事物的兩種不同方式而已,如果情況真的是這樣,那麽對偶性假設將對我們理解物理學產生深遠的影響。我們知道,對於強作用而言,假設場與弦的對偶性正是弦論誕生最初的動機,同樣對於π介子,長程Weyl規範的作用也很像弦,弦將正反兩個誇克連接起來,長程Weyl規範則強調了正反兩個誇克之間的對合關系。長程Weyl規範與楊規範有直接的聯系,不過長程Weyl規範著重刻劃了時空的彎曲程度。
對偶性假設告訴我們,兩個看起來不同的現象其實只是描述同一事物的兩種不同方式而已,如果情況真的是這樣,那麽對偶性假設將對我們理解物理學產生深遠的影響。我們知道,對於強作用而言,假設場與弦的對偶性正是弦論誕生最初的動機,同樣對於π介子,長程Weyl規範的作用也很像弦,弦將正反兩個誇克連接起來,長程Weyl規範則強調了正反兩個誇克之間的對合關系。長程Weyl規範與楊規範有直接的聯系,不過長程Weyl規範著重刻劃了時空的彎曲程度。
圈量子引力中的對偶性假設
圈量子引力的創始人Alexander Polyakov告訴我們,他試圖中從理論中找出一段量子化的電流圈是基本實體的描述,他的信仰完全是一個關於對偶性假設的宣言。對偶性思想仍然是基本粒子物理和圈量子引力研究的一個主要驅動力,即使對偶性沒有解決啟發人們發明它的問題,它仍然被證明是圈量子引力論的中心概念。
量子細胞場論與Wilson的格點理論以及圈量子引力都是有聯系的,而且量子細胞場論是從最為基礎的量子力學假設導出類似的結果。在量子細胞場論中,位置與動量的本征值都是連續的,但由於量子細胞周期的存在,能量或者其它算符的譜是不連續的,如果我們要求黑洞內各個量子細胞之間的周期同步的話,那麽自然也可以得出自旋網絡或者Knot等結論。
引力子看起來很像閉弦,所以你也可以將Weyl規範看成是閉弦沿世界面積分得到的一個規範;但長程Weyl規範只對玻色子產生起作用,所以我們回歸的是那個不需要超對稱不需要費米弦的最原始的弦論;弦論之所以引入超對稱性,是因為弦論中要納入引力子必須有超對稱性,長程Weyl規範具有引力子所需的對稱性。引力子實際上是由兩個長程Weyl規範刻劃的,考慮兩個產生引力相互作用的物質粒子,分別圍著兩個物質粒子畫兩個小圓,這兩個小圓相交於根軸上的兩個無窮遠虛圓點,這兩個無窮小虛圓點產生了引力子的橫向極化部分,兩個物質粒子之間的對合關系產生了引力子的縱向極化部分。量子細胞引力論勝過圈量子引力之處在於量子細胞引力論是協變量子化的,圈量子引力論是正則量子化的。
量子細胞場論與Wilson的格點理論以及圈量子引力都是有聯系的,而且量子細胞場論是從最為基礎的量子力學假設導出類似的結果。在量子細胞場論中,位置與動量的本征值都是連續的,但由於量子細胞周期的存在,能量或者其它算符的譜是不連續的,如果我們要求黑洞內各個量子細胞之間的周期同步的話,那麽自然也可以得出自旋網絡或者Knot等結論。
引力子看起來很像閉弦,所以你也可以將Weyl規範看成是閉弦沿世界面積分得到的一個規範;但長程Weyl規範只對玻色子產生起作用,所以我們回歸的是那個不需要超對稱不需要費米弦的最原始的弦論;弦論之所以引入超對稱性,是因為弦論中要納入引力子必須有超對稱性,長程Weyl規範具有引力子所需的對稱性。引力子實際上是由兩個長程Weyl規範刻劃的,考慮兩個產生引力相互作用的物質粒子,分別圍著兩個物質粒子畫兩個小圓,這兩個小圓相交於根軸上的兩個無窮遠虛圓點,這兩個無窮小虛圓點產生了引力子的橫向極化部分,兩個物質粒子之間的對合關系產生了引力子的縱向極化部分。量子細胞引力論勝過圈量子引力之處在於量子細胞引力論是協變量子化的,圈量子引力論是正則量子化的。
量子場論有問題的地方
閔可夫斯基時空觀將平直時空的楊規範與彎曲時空的Weyl規範割裂開來,Bohm-Aharonov效應告訴我們規範勢是有實質物理意義的場量,借助於主叢上的聯絡理論可以產生長程Weyl規範引起的彎曲效應。在量子細胞場論中,規範玻色子的測地線是龐加萊雙曲測地線,這實際上是經過了Gupta-Bleuler量子化,矢量分量與標量分量抵消後剩余的那部分雙曲庫侖分量,這就是“神學”的好處,我們可以直接處理真正起主導作用的場量。
這個雙曲庫侖分量帶有膠子的相位信息,從對合點的一處移到對應點膠子的相位會轉過180度;從這裏可以分析出單重橢圓幾何與雙重橢圓幾何對偶性的根源,這正是量子場論和弦論都忽略的地方。假設哼哈子從核子表面的一點移到它的對徑點上,哼哈子的自旋為0,而誇克的整體相位轉過了180度;膠子場產生的整體180度旋轉與誇克場產生的整體180度旋轉同步起來,產生了自旋為0的π介子場。這裏可以借助路徑積分量子化探討一下哼哈子產生的根源,哼哈子可能只是一種數學對象,與哼哈子路徑相距較遠的那部分場的相位抵消的很厲害,只剩下離哼哈子路徑相距較近的這部分波函數會相互增強,對應的正是路徑積分中所謂的經典路徑,QCD求和規則很繁瑣,我們的推導簡單明了。當然你會說路徑積分量子化只是針對一次量子化的,不知道有沒有人推廣到二次量子化情形,但我們先借用一下也無妨。
廣義相對論的精髓是時空的彎曲效應產生了引力場,這正是量子場論出問題的地方,引力場本質上是一種二階的場,用一階場的楊規範去量子化當然會出問題,長程的Weyl規範自然帶了彎曲時空的度量,這與現代大範圍拓撲場論的中心思想是一致的。量子細胞引力論走的是一條中庸之道,牛頓引力論認為引力是一種超距作用,廣義相對論將引力的起源放到了一點上,當然會產生無窮大和奇點之說;對合關系引出的Weyl規範自然排除了超距作用,同時一階楊規範引起的無窮大一開始就被排除了;量子細胞引力論是背景無關的理論,而弦論是一種背景相關的理論;正因為如此,量子細胞場論才能在量子場論和弦論出問題的地方占據一片天空。
這個雙曲庫侖分量帶有膠子的相位信息,從對合點的一處移到對應點膠子的相位會轉過180度;從這裏可以分析出單重橢圓幾何與雙重橢圓幾何對偶性的根源,這正是量子場論和弦論都忽略的地方。假設哼哈子從核子表面的一點移到它的對徑點上,哼哈子的自旋為0,而誇克的整體相位轉過了180度;膠子場產生的整體180度旋轉與誇克場產生的整體180度旋轉同步起來,產生了自旋為0的π介子場。這裏可以借助路徑積分量子化探討一下哼哈子產生的根源,哼哈子可能只是一種數學對象,與哼哈子路徑相距較遠的那部分場的相位抵消的很厲害,只剩下離哼哈子路徑相距較近的這部分波函數會相互增強,對應的正是路徑積分中所謂的經典路徑,QCD求和規則很繁瑣,我們的推導簡單明了。當然你會說路徑積分量子化只是針對一次量子化的,不知道有沒有人推廣到二次量子化情形,但我們先借用一下也無妨。
廣義相對論的精髓是時空的彎曲效應產生了引力場,這正是量子場論出問題的地方,引力場本質上是一種二階的場,用一階場的楊規範去量子化當然會出問題,長程的Weyl規範自然帶了彎曲時空的度量,這與現代大範圍拓撲場論的中心思想是一致的。量子細胞引力論走的是一條中庸之道,牛頓引力論認為引力是一種超距作用,廣義相對論將引力的起源放到了一點上,當然會產生無窮大和奇點之說;對合關系引出的Weyl規範自然排除了超距作用,同時一階楊規範引起的無窮大一開始就被排除了;量子細胞引力論是背景無關的理論,而弦論是一種背景相關的理論;正因為如此,量子細胞場論才能在量子場論和弦論出問題的地方占據一片天空。
埃舍爾的版畫
下圖是Escher的版畫,形象地描繪了Lobatchevsky幾何:

我們發現Lobatchevsky幾何與龐加萊雙曲幾何是對偶的,這種對偶性類似於單重橢圓幾何與雙重橢圓幾何的對偶性,單重橢圓幾何與龐加萊雙曲幾何對偶,雙重橢圓幾何與Lobatchevsky幾何對偶;這種對偶性是一種動態對偶性,不知道數學家們是否早已發現了這種對偶性,美國新數學叢書《幾何變換》第四冊有用到龐加萊雙曲模型證明Lobatchevsky的命題,可惜的是唯獨第四冊沒有中譯本,所以我們也不知道這算不算是幾何學上的一個新發現。
這種對偶性也是射影空間中角度變換與平移變換對偶性關系的一個擴充。如果量子場論中的軸子或者軸矢量之類的服從Lobatchevsky幾何,那麽就直接排除了真空凝聚的可能性,也就排除了真空自發性破缺的可能性;換句話說,量子場論的許多推論前提都是錯的,唯一可能正確的理論只有量子細胞場論,而且看起來這種服從Lobatchevsky幾何的可能性非常大。

我們發現Lobatchevsky幾何與龐加萊雙曲幾何是對偶的,這種對偶性類似於單重橢圓幾何與雙重橢圓幾何的對偶性,單重橢圓幾何與龐加萊雙曲幾何對偶,雙重橢圓幾何與Lobatchevsky幾何對偶;這種對偶性是一種動態對偶性,不知道數學家們是否早已發現了這種對偶性,美國新數學叢書《幾何變換》第四冊有用到龐加萊雙曲模型證明Lobatchevsky的命題,可惜的是唯獨第四冊沒有中譯本,所以我們也不知道這算不算是幾何學上的一個新發現。
這種對偶性也是射影空間中角度變換與平移變換對偶性關系的一個擴充。如果量子場論中的軸子或者軸矢量之類的服從Lobatchevsky幾何,那麽就直接排除了真空凝聚的可能性,也就排除了真空自發性破缺的可能性;換句話說,量子場論的許多推論前提都是錯的,唯一可能正確的理論只有量子細胞場論,而且看起來這種服從Lobatchevsky幾何的可能性非常大。
一種最簡單的統一場論
我們又用了最簡單的統一場論的名字,不過這一回是指量子細胞場論是一種線性化的量子場論和廣義相對論。如果將構建統一場論比喻為攀登珠穆朗瑪峰,量子場論和廣義相對論將我們帶到了珠峰大本營,而量子細胞場論則等於到達了前進營地。Yang-Mills場和廣義相對論的引力場都有著非線性的性質,即引力子和規範玻色子都會發生較強的自作用。打個比方說,量子場論和廣義相對論都將旅行中的汽車和火車當成了場的一部分,對於到達珠峰大本營來說,汽車和火車都是必要的交通工具,但真正開始攀登珠峰,我們就應當擺脫這些交通工具而輕裝上陣。量子細胞場論中的規範玻色子相當於滿足對偶性的孤子,在低能情況下沒有自作用,場的方程是線性的,這同量子力學中的Hilbert空間的看法是一致的,Hilbert空間是線性空間。
當然在高能情況下,我們仍然可以由線性關系導出規範玻色子的自作用,由線性關系導出非線性是容易的,反之則要麻煩得多。量子場論和廣義相對論中的無窮大來自於量子邏輯,我們知道量子邏輯的基礎是直覺邏輯,關於公理化量子場論的詳細內容可參見Wightman的原著,我們要強調的是在直覺邏輯中你可以隨意的復制或者刪除一個假設,這同二次量子化中你可以隨意復制或者湮滅一個虛粒子是一樣的。量子細胞場論基於的則是線性邏輯,關於線性邏輯的詳情可參見Andrea Asperti, Giuseppe Longo所寫的範疇論一書,線性邏輯尊重資源有限的事實,你不能再任意地復制或者刪除一個假設,但如果你想復制虛粒子則可以將直覺邏輯嵌入到線性邏輯中,有兩種嵌入的方式,兩種對偶的嵌入方式對應的正是由色力生成核力的機制。
當然在高能情況下,我們仍然可以由線性關系導出規範玻色子的自作用,由線性關系導出非線性是容易的,反之則要麻煩得多。量子場論和廣義相對論中的無窮大來自於量子邏輯,我們知道量子邏輯的基礎是直覺邏輯,關於公理化量子場論的詳細內容可參見Wightman的原著,我們要強調的是在直覺邏輯中你可以隨意的復制或者刪除一個假設,這同二次量子化中你可以隨意復制或者湮滅一個虛粒子是一樣的。量子細胞場論基於的則是線性邏輯,關於線性邏輯的詳情可參見Andrea Asperti, Giuseppe Longo所寫的範疇論一書,線性邏輯尊重資源有限的事實,你不能再任意地復制或者刪除一個假設,但如果你想復制虛粒子則可以將直覺邏輯嵌入到線性邏輯中,有兩種嵌入的方式,兩種對偶的嵌入方式對應的正是由色力生成核力的機制。

No comments:
Post a Comment