一般室溫. 25°C 約僅相當於0.025eV 的能量, 家用兩孔插座的電壓 110 電子伏特),1TeV相當于一只蚊子飛行的能量,但質子只是蚊子的千億分之一
A Leap in Energy
The discovery by BICEP2 of the signature of gravitational waves in the cosmic microwave background — if it holds up! — is not only good evidence for inflation in the very early universe, it’s a fairly precise indication that inflation occurred at a very high energy scale. I thought of a vivid way to emphasize just how high that energy is.
Particle physicists like to keep things simple by characterizing all physical quantities in terms of a single kind of unit — typically energy, and typically measured in electron volts. That’s part of the magic of natural units. We live in a world governed by relativity, so the speed of light c provides a natural unit of velocity. We also live in a world governed by quantum mechanics, so Planck’s constant ℏ provides a natural unit of action. And we live in a world governed by statistical mechanics, so Boltzmann’s constant k provides a natural conversion between energy and temperature. We therefore set these quantities equal to unity, ℏ = c = k = 1. Once that’s done, mass and temperature have the same units as energy. Time and distance have units of 1/energy. Energy density is energy per unit spatial volume, which works out to (energy)4. This kind of reasoning makes particle physicists happy, since they like to think of everything in terms of energy scales.
So, thinking about everything in terms of energy scales, what’s the energy of everyday life? It makes sense to choose room temperature, about 295 Kelvin. That works out to about 0.02 electron volts, which we can call the temperature of everyday life:
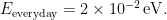
One way of thinking about the progress of fundamental physics is to track the progress of our understanding to higher and higher energy scales. The highest energies we’ve ever probed in experiments here on Earth are those at the Large Hadron Collider. The last run of the LHC reached energies of 8 TeV, or 8×1012 eV. But it would be an exaggeration to say that we really understand those energies; when protons collide at the LHC, their energies are distributed among a number of particles in each event. That’s why the heaviest particles we’ve ever found are the Higgs boson and the top quark, both with masses a bit under 0.2 TeV. So let’s call that the highest energy we’ve understood through experiments here on Earth:

Thus, the progress of science has extended our understanding a factor of 1013, thirteen orders of magnitude, above our everyday experience:

Not too shabby, for a species of jumped-up apes with only an intermittent dedication to the ideals of rationality and empiricism.
Now let’s turn to inflation. The great thing about detecting gravitational waves in the CMB is that, in contrast with the density perturbations we’ve known about for some time, the gravitational wave amplitude depends solely on the expansion rate during inflation, not on any details about the scalar-field potential. And the expansion rate is directly related to the energy density (energy to the fourth power) by general relativity itself. So measuring the amplitude, as BICEP2 did, tells us the inflationary energy scale directly. And the answer is:
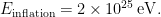
For comparison, the reduced Planck energy (where “reduced” means “including the factor of 8π where it should be”) is 2×1027 eV, a mere stone’s throw away.
So, you can do the math yourself. Inflation was going on at energy scales that exceed those we explore here on Earth by a factor of about
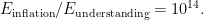
In other words, BICEP2 has extended our experimental reach, as measured by energy scale, by an amount (1014) slightly larger than the total previous progress of all of science (1013).
We don’t, of course, understand everything between LHC energies and inflationary energies, not even close. But we (the royal “we”) have been able to make an enormous extrapolation, using scientific reasoning, and get the right answer. It’s a big deal.
Particle physicists like to keep things simple by characterizing all physical quantities in terms of a single kind of unit — typically energy, and typically measured in electron volts. That’s part of the magic of natural units. We live in a world governed by relativity, so the speed of light c provides a natural unit of velocity. We also live in a world governed by quantum mechanics, so Planck’s constant ℏ provides a natural unit of action. And we live in a world governed by statistical mechanics, so Boltzmann’s constant k provides a natural conversion between energy and temperature. We therefore set these quantities equal to unity, ℏ = c = k = 1. Once that’s done, mass and temperature have the same units as energy. Time and distance have units of 1/energy. Energy density is energy per unit spatial volume, which works out to (energy)4. This kind of reasoning makes particle physicists happy, since they like to think of everything in terms of energy scales.
So, thinking about everything in terms of energy scales, what’s the energy of everyday life? It makes sense to choose room temperature, about 295 Kelvin. That works out to about 0.02 electron volts, which we can call the temperature of everyday life:
One way of thinking about the progress of fundamental physics is to track the progress of our understanding to higher and higher energy scales. The highest energies we’ve ever probed in experiments here on Earth are those at the Large Hadron Collider. The last run of the LHC reached energies of 8 TeV, or 8×1012 eV. But it would be an exaggeration to say that we really understand those energies; when protons collide at the LHC, their energies are distributed among a number of particles in each event. That’s why the heaviest particles we’ve ever found are the Higgs boson and the top quark, both with masses a bit under 0.2 TeV. So let’s call that the highest energy we’ve understood through experiments here on Earth:
Thus, the progress of science has extended our understanding a factor of 1013, thirteen orders of magnitude, above our everyday experience:
Not too shabby, for a species of jumped-up apes with only an intermittent dedication to the ideals of rationality and empiricism.
Now let’s turn to inflation. The great thing about detecting gravitational waves in the CMB is that, in contrast with the density perturbations we’ve known about for some time, the gravitational wave amplitude depends solely on the expansion rate during inflation, not on any details about the scalar-field potential. And the expansion rate is directly related to the energy density (energy to the fourth power) by general relativity itself. So measuring the amplitude, as BICEP2 did, tells us the inflationary energy scale directly. And the answer is:
For comparison, the reduced Planck energy (where “reduced” means “including the factor of 8π where it should be”) is 2×1027 eV, a mere stone’s throw away.
So, you can do the math yourself. Inflation was going on at energy scales that exceed those we explore here on Earth by a factor of about
In other words, BICEP2 has extended our experimental reach, as measured by energy scale, by an amount (1014) slightly larger than the total previous progress of all of science (1013).
We don’t, of course, understand everything between LHC energies and inflationary energies, not even close. But we (the royal “we”) have been able to make an enormous extrapolation, using scientific reasoning, and get the right answer. It’s a big deal.
No comments:
Post a Comment