根據
柯西邊界條件(
Cauchy boundary condition),有時候,給定在邊界曲面的法向電場與電勢,可能會因為給定過多邊界條件,而造成無法計算出一致的電勢的狀況。實際而言,只要給定法向電場或電勢,兩者之一,就可以計算出電勢。
[4]
假若積分體積為無窮大空間,當

趨向於無窮大時,則面積分的被積分項目會以

速率遞減,而積分面積會以
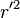
速率遞增,所以,面積分項目會趨向於零,這方程式約化為先前的電勢方程式
設定在無窮遠的電勢為參考值0,則在任意位置的電勢為
 ;
;
http://zh.wikipedia.org/wiki/%E9%9B%BB%E5%8B%A2
 趨向於無窮大時,則面積分的被積分項目會以
趨向於無窮大時,則面積分的被積分項目會以  速率遞減,而積分面積會以
速率遞減,而積分面積會以 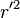 速率遞增,所以,面積分項目會趨向於零,這方程式約化為先前的電勢方程式
速率遞增,所以,面積分項目會趨向於零,這方程式約化為先前的電勢方程式 ;
;
No comments:
Post a Comment