在静電學裏,電勢(electric potential)定義為處於電場中某个位置的單位電荷所具有的電勢能。[1]電勢又稱為電位,是純量,其數值不具有絕對意義,只具有相對意義。為了便於分析問題,必需設定參考位置。通常,一個明智的選擇是將在無窮遠位置的電勢設定為零。那麼,電勢可以做如此工作定義:假設檢驗電荷從無窮遠位置,經過任意路徑,抗拒電場力,緩慢地遷移到某位置,則在這位置的電勢,等於因遷移所做的機械功與檢驗電荷量的比值。
電勢
维基百科,自由的百科全书
電勢必需滿足帕松方程式,同時符合相關邊界條件;假設在某區域內的電荷密度為零,則帕松方程式約化為拉普拉斯方程式,電勢必需滿足拉普拉斯方程式。
在電動力學裏,當含時電磁場存在的時候,電勢可以延伸為「廣義電勢」。特別注意,廣義電勢不能被視為電勢能每單位電荷。
目录[隐藏] |
[编辑] 簡介
處於外電場的帶電粒子會感受到外電場施加的作用力,稱為電場力,促使帶電粒子呈加速度運動。對於帶正電粒子,電場力與電場同方向;對於帶負電粒子,電場力與電場反方向。電場力的數值大小與電荷量、電場數值大小成正比。作用力與勢能之間有非常直接的關係。隨著物體朝著作用力的方向呈加速度運動,物體的動能變大,勢能變小。例如,一個石頭在山頂的勢能大於在山腳的勢能。隨著物體滾落,勢能變小,動能變大。
對於某種特別作用力,科學家可以定義其向量場和其位勢,使得物體因為這向量場而具有的勢能,只相依於物體位置與參考位置之間的距離。稱這種作用力為保守力,這種向量場為保守場。
例如,重力、靜電場的電場力,都是保守力。靜電場的純量勢稱為電勢,或稱為靜電勢。
電勢和磁向量勢共同形成一個四維向量,稱為四維勢。從某一個慣性參考系觀察到的四維勢,應用勞侖茲變換,可以計算出另外一個慣性參考系所觀察到的四維勢。
[编辑] 靜電學裏的電勢
在靜電學裏,電場 內某位置
內某位置  的電勢
的電勢  ,以方程式定義為[1]
,以方程式定義為[1] ;
;
 是在位置
是在位置  的檢驗電荷
的檢驗電荷  所具有的電勢能。
所具有的電勢能。電勢能的數值是人為設定的,沒有絕對意義,只有相對於某參考位置的已設定參考值,才有物理意義。假若要設定電勢能在空間任意位置的數值,必須先設定其在某參考位置
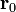 的數值。為了方便運算,假設其參考數值為0。然後,就可以將在位置
的數值。為了方便運算,假設其參考數值為0。然後,就可以將在位置  的電勢能
的電勢能  定義為從參考位置
定義為從參考位置 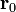 緩慢地將檢驗電荷
緩慢地將檢驗電荷  遷移至
遷移至  所需做的機械功
所需做的機械功  :
: 。
。
 ,必需恰巧抵消處於電場
,必需恰巧抵消處於電場  的檢驗電荷
的檢驗電荷  所感受到的電場力
所感受到的電場力  ,即
,即  。機械功等於外力
。機械功等於外力  的路徑積分:
的路徑積分: ;
;
 是從參考位置
是從參考位置 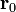 到位置
到位置  的一條任意路徑,
的一條任意路徑,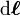 是微小線元素。
是微小線元素。在靜電學裏,
 ,電場是保守場,所以,在積分時,可以選擇任意路徑
,電場是保守場,所以,在積分時,可以選擇任意路徑  ,計算出來的結果都一樣。更詳盡細節,請參閱條目保守力。由於這方程式右手邊的路徑積分不相依於路徑
,計算出來的結果都一樣。更詳盡細節,請參閱條目保守力。由於這方程式右手邊的路徑積分不相依於路徑  ,只相依於路徑的初始位置
,只相依於路徑的初始位置 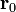 與終止位置
與終止位置  。若能夠假設無窮遠位置
。若能夠假設無窮遠位置  的電勢能為 0 ,則可以設定參考位置
的電勢能為 0 ,則可以設定參考位置 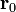 在無窮遠位置
在無窮遠位置  :
: 。
。
 。
。
 、
、 之間的「電勢差」
之間的「電勢差」  為
為 。
。
 是保守場,電勢差也與積分路徑無關,只跟積分路徑的初始位置與終止位置有關。
是保守場,電勢差也與積分路徑無關,只跟積分路徑的初始位置與終止位置有關。[编辑] 疊加原理
電場遵守疊加原理:假設在三維空間裏,由兩組完全不相交的電荷分佈所產生的電場分別為 、
、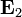 ,則總電場為
,則總電場為  。
。總電勢為抗拒總電場力所做的機械功每單荷電量:
 。
。
[编辑] 電勢的微分方程式
應用積分符號內取微分方法,電勢的梯度為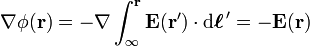 。
。
 。
。
 ;
;
 是電荷密度,
是電荷密度,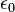 是電常數。
是電常數。所以,電勢滿足帕松方程式:
 。
。
 。
。
 ,也就是說,電場不具保守性(由於隨時間變化的磁場造成的效應;參閱馬克士威方程組),則不能使用這些方程式。
,也就是說,電場不具保守性(由於隨時間變化的磁場造成的效應;參閱馬克士威方程組),則不能使用這些方程式。由於電勢乃是純量,而電場是具有三個分量的向量,所以,很多時候,使用電勢來解析問題會省去很多運算工作,帶來很大的便利。
[编辑] 拉普拉斯方程式的解答
在某空間區域內,假設電荷密度為零,則電勢必須滿足拉普拉斯方程式,並且符合所有相關邊界條件。[编辑] 邊界條件
在靜電學裏,有三種邊界條件:- 狄利克雷邊界條件:在所有邊界,電勢都已良態給定。具有這種邊界條件的問題稱為狄利克雷問題。
- 紐曼邊界條件:在所有邊界,電勢的法向導數都已良態給定。具有這種邊界條件的問題稱為紐曼問題。
- 混合邊界條件:一部分邊界的電勢都已良態給定,其它邊界的電勢的法向導數也已良態給定。
[编辑] 分離變數法
應用分離變數法來解析拉普拉斯方程式,可以將問題的偏微分方程式改變為一組較容易解析的常微分方程式。對於一般問題,通常會採用直角坐標系、圓柱坐標系或球坐標系來分離拉普拉斯方程式。但是,對於其它比較特別的問題,另外還有八種坐標系可以用來分離拉普拉斯方程式。[2]分離之後,找到每一個常微分方程式的通解(通常為一組本徵方程式的疊加),電勢可以表達為這些通解的乘積。將這表達式與邊界條件相匹配,就可以設定一般解的係數,從而找到問題的特解。根據拉普拉斯方程式的唯一性定理,這特解也是唯一的正確解答。[编辑] 兩個半平面導體案例
假設在xy-平面的無限平面導體被一條位於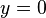 的絕緣線條分為兩半,兩個處於y+、y--半平面的導體的電勢分別設定為
的絕緣線條分為兩半,兩個處於y+、y--半平面的導體的電勢分別設定為  、
、 ,則計算z+-半空間任意位置的電勢這問題,由於邊界條件的幾何形狀適合用直角坐標來描述,可以以直角坐標
,則計算z+-半空間任意位置的電勢這問題,由於邊界條件的幾何形狀適合用直角坐標來描述,可以以直角坐標  將拉普拉斯方程式表示為:
將拉普拉斯方程式表示為: 。
。
 。
。
 。
。
 。
。
 、
、 。
。
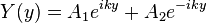 、
、 ;
;
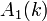 、
、 、
、 、
、 都是係數函數。
都是係數函數。當
 趨向於無窮大時,
趨向於無窮大時,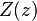 趨向於零,所以,
趨向於零,所以, 。綜合起來,電勢為
。綜合起來,電勢為 。
。
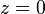 ,y+、y--半平面的電勢分別為
,y+、y--半平面的電勢分別為  、
、 ,所以,
,所以,- 當
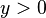 時,
時, 、
、 - 當
 時,
時, 。
。
 、
、 。
。
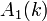 項目貢獻出的電勢為
項目貢獻出的電勢為 。
。
 項目貢獻出的電勢為
項目貢獻出的電勢為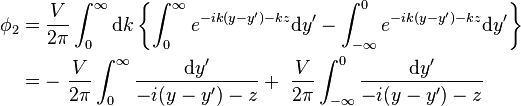 。
。
 。
。
[编辑] 帕松方程式的解答
[编辑] 電荷分佈所產生的電勢
根據庫侖定律,一個源位置為 的點電荷
的點電荷  ,所產生在任意位置
,所產生在任意位置  的電場為
的電場為 。
。
 內部電荷密度為
內部電荷密度為  的電荷分佈,在檢驗位置
的電荷分佈,在檢驗位置  所產生的電場為
所產生的電場為 ;
;
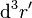 是微小體積元素。
是微小體積元素。應用一條向量恆等式,
 ,
,
 。
。
 ;(1)
;(1)
 ,
,
 在積分體積
在積分體積  內,則可得到帕松方程式:
內,則可得到帕松方程式: 。
。
[编辑] 邊界條件
電勢的方程式(1)只考慮到一群電荷分佈所產生的電勢。假若遭遇邊界條件為電勢的靜電學問題,就不能使用方程式(1),必需使用更具功能的方法。根據格林第二恆等式,對於任意良態函數
 與
與  ,[4]
,[4] ;
;
 是積分體積,
是積分體積, 是包住
是包住  的閉表面,
的閉表面, 是微小面元素,
是微小面元素, 或
或  都是取垂直於閉表面
都是取垂直於閉表面  的法向導數,都是從積分體積
的法向導數,都是從積分體積  朝外指出。
朝外指出。設定
 為在
為在  的電勢,
的電勢, 為
為  與
與  之間的距離。應用帕松方程式
之間的距離。應用帕松方程式  ,則可得到
,則可得到![\int_{\mathbb{V}'} \left[ \phi(\mathbf{r}') \nabla^2 \left(\frac{1}{|\mathbf{r} - \mathbf{r}'|}\right) + \frac{\rho(\mathbf{r}')}{\epsilon_0 |\mathbf{r} - \mathbf{r}'|} \right]\mathrm{d}^3 r' = \oint_{\mathbb{S}'} \left[ \phi\ {\partial \over \partial n'}\left(\frac{1}{|\mathbf{r} - \mathbf{r}'|}\right) - \left(\frac{1}{|\mathbf{r} - \mathbf{r}'|}\right) {\partial \phi \over \partial n'}\right]\mathrm{d}^2 r'](http://upload.wikimedia.org/math/0/6/6/0666a16ab77b28d7d2f14a40e6c82b38.png) 。
。
 。
。
 在積分體積
在積分體積  內,則可得到
內,則可得到![\phi(\mathbf{r}) =\frac{1}{4 \pi \epsilon_0} \int_{\mathbb{V}'} \frac{\rho(\mathbf{r}')}{|\mathbf{r} - \mathbf{r}'|}\ \mathrm{d}^3 r' +\frac{1}{4 \pi}\oint_{\mathbb{S}'} \left[\left(\frac{1}{|\mathbf{r} - \mathbf{r}'|}\right) {\partial \phi \over \partial n'}-\phi\ {\partial \over \partial n'}\left(\frac{1}{|\mathbf{r} - \mathbf{r}'|}\right)\right]\mathrm{d}^2 r'](http://upload.wikimedia.org/math/c/0/7/c07b8f8131cde68bc5ac72ca7d2ea02b.png) 。
。
 體內與體外之間的邊界曲面。面積分的第一個項目要求給定在邊界曲面的法向電場,即
體內與體外之間的邊界曲面。面積分的第一個項目要求給定在邊界曲面的法向電場,即  ,也就是面感應電荷密度
,也就是面感應電荷密度  。面積分的第二個項目要求給定在邊界曲面的電勢
。面積分的第二個項目要求給定在邊界曲面的電勢  。假若能夠知道積分體積內的電荷密度、在閉曲面的面電荷密度與電勢,就可以計算出在積分體積內任意位置的電勢。
。假若能夠知道積分體積內的電荷密度、在閉曲面的面電荷密度與電勢,就可以計算出在積分體積內任意位置的電勢。根據柯西邊界條件(Cauchy boundary condition),有時候,給定在邊界曲面的法向電場與電勢,可能會因為給定過多邊界條件,而造成無法計算出一致的電勢的狀況。實際而言,只要給定法向電場或電勢,兩者之一,就可以計算出電勢。[4]
假若積分體積為無窮大空間,當
 趨向於無窮大時,則面積分的被積分項目會以
趨向於無窮大時,則面積分的被積分項目會以  速率遞減,而積分面積會以
速率遞減,而積分面積會以  速率遞增,所以,面積分項目會趨向於零,這方程式約化為先前的電勢方程式(1)。
速率遞增,所以,面積分項目會趨向於零,這方程式約化為先前的電勢方程式(1)。[编辑] 格林函數
包括函數 在內,有一類函數
在內,有一類函數  ,稱為格林函數,能夠滿足方程式
,稱為格林函數,能夠滿足方程式 。
。
 滿足拉普拉斯方程式
滿足拉普拉斯方程式 ,
,
 也是格林函數。
也是格林函數。應用這靈活性質,可以更嚴格地規定格林函數:[4]
- 對於狄利克雷問題,當源位置
 在邊界表面
在邊界表面  時,規定格林函數
時,規定格林函數 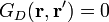 。這樣,從格林第二恆等式,設定
。這樣,從格林第二恆等式,設定  為在
為在  的電勢,
的電勢, ,則可得到
,則可得到
-
 。(2)
。(2)
- 對於滿足紐曼問題,當源位置
 在邊界表面
在邊界表面  時,規定格林函數
時,規定格林函數  。
。
[编辑] 無限平面導體案例
 ;
;
 、
、 分別是檢驗位置
分別是檢驗位置  、源位置
、源位置  的直角坐標。
的直角坐標。由於接地導體的電勢為零,方程式(2)的面積分項目等於零,方程式(2)變為
 。
。
 有點電荷
有點電荷  ,則在z+半空間任意位置的電勢為
,則在z+半空間任意位置的電勢為 。
。
 所產生的電勢;右手邊第二個項目,是使用鏡像法時,鏡像電荷
所產生的電勢;右手邊第二個項目,是使用鏡像法時,鏡像電荷  所產生的電勢。請參閱鏡像法條目的點電荷與無限平面導體段落。
所產生的電勢。請參閱鏡像法條目的點電荷與無限平面導體段落。[编辑] 導引
已知函數 為格林函數
為格林函數  ,滿足方程式
,滿足方程式 。
。
 的傅立葉級數為[2]
的傅立葉級數為[2] 。
。
 ,滿足狄利克雷邊界條件
,滿足狄利克雷邊界條件 ,同時,函數
,同時,函數  滿足拉普拉斯方程式
滿足拉普拉斯方程式 。
。
 以傅立葉級數擴張為
以傅立葉級數擴張為![\begin{align}H(\mathbf{r},\mathbf{r}')
& = \frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ \mathrm{d}k_x\ \mathrm{d}k_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\ \mathrm{d}k_z \left[B(\mathbf{k},z')e^{ik_z z} +C(\mathbf{k},z')e^{-ik_z z}\right]\\
\end{align}](http://upload.wikimedia.org/math/9/4/3/9432541b3c22dacf59a7e866f7e96fc2.png) 。
。
 函數與
函數與  函數的形式相同。這是因為對於無限空間案例與無限平面導體案例,兩種案例的x-邊界條件與y-邊界條件都相同,只有z-邊界條件稍有改變。將
函數的形式相同。這是因為對於無限空間案例與無限平面導體案例,兩種案例的x-邊界條件與y-邊界條件都相同,只有z-邊界條件稍有改變。將  函數的方程式代如,
函數的方程式代如, 變為
變為![G_D(\mathbf{r},\mathbf{r}')
= \frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ \mathrm{d}k_x\ \mathrm{d}k_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\ \mathrm{d}k_z \left[\frac{e^{ik_z(z-z')}}{k_x^2+k_y^2+k_z^2} +B(\mathbf{k},z')e^{ik_z z} +C(\mathbf{k},z')e^{-ik_z z}\right]](http://upload.wikimedia.org/math/4/f/b/4fb35627714da67f4ff74cf943938a71.png) ;
;
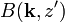 與
與  都是係數函數。
都是係數函數。由於
 ,對於任意
,對於任意  與
與  ,
,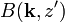 與
與  之間的關係為
之間的關係為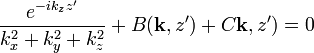 、
、 、
、 ;
;
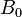 與
與  都是係數常數,而且,
都是係數常數,而且,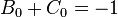
將這些公式代入
 ,可以得到
,可以得到![G_D(\mathbf{r},\mathbf{r}')
= \frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ \mathrm{d}k_x\ \mathrm{d}k_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\ \mathrm{d}k_z \left\{\frac{(1+B_0)}{k^2} \left[ e^{ik_z(z-z')}-e^{ik_z(z+z')}\right]\right\}](http://upload.wikimedia.org/math/7/f/0/7f075ff63438f8842a8615f8a361b4e2.png) 。
。
 ,必需設定
,必需設定  。所以,
。所以,![\begin{align}G_D(\mathbf{r},\mathbf{r}') & = \frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ \mathrm{d}k_x\ \mathrm{d}k_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\ \mathrm{d}k_z \left\{\frac{1}{k^2} \left[ e^{ik_z(z-z')}-e^{ik_z(z+z')}\right]\right\} \\
& =\frac{1}{|\mathbf{r} - \mathbf{r}'|}-\frac{1}{|\mathbf{r} - \mathbf{r}''|} \\
& =\cfrac{1}{\sqrt{(x-x')^2+(y-y')^2+ (z - z')^2}} -\ \cfrac{1}{\sqrt{(x-x')^2+(y-y')^2+(z+z')^2}} \\
\end{align}](http://upload.wikimedia.org/math/6/5/9/65994ccec3d97dc7fa9426bd0f7e9e5a.png) ;
;
 是鏡像電荷的位置。
是鏡像電荷的位置。[编辑] 兩個半平面導體案例
假設在xy-平面的無限平面導體被一條位於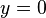 的絕緣線條分為兩半,兩個處於y+、y--半平面的導體的電勢分別設定為
的絕緣線條分為兩半,兩個處於y+、y--半平面的導體的電勢分別設定為  與
與  ,則由於
,則由於  ,方程式(2)變為
,方程式(2)變為 。(3)
。(3)
 是z+-半空間,xy-平面是其邊界閉曲面的一部分,格林函數在xy-平面的法向導數的方向是朝著負z方向:
是z+-半空間,xy-平面是其邊界閉曲面的一部分,格林函數在xy-平面的法向導數的方向是朝著負z方向:![\begin{align}{\partial G_D\over \partial n'} & =-\ {\partial G_D\over \partial z'} \\
& =-\ \cfrac{z - z'}{[(x-x')^2+(y-y')^2+ (z - z')^2]^{3/2}}\ -\ \cfrac{z + z'}{[(x-x')^2+(y-y')^2+(z+z')^2]^{3/2}} \\
& =-\ \cfrac{2z}{[(x-x')^2+(y-y')^2+ z^2]^{3/2}} \\
\end{align}](http://upload.wikimedia.org/math/2/9/9/299f5c0659985db41f8249ae3a3c99b7.png) 。
。
 的邊界閉曲面在無窮遠位置的電勢為0,所以,只需要計算xy-平面給出的貢獻,就可以得到在
的邊界閉曲面在無窮遠位置的電勢為0,所以,只需要計算xy-平面給出的貢獻,就可以得到在  內部任意位置的電勢。將上述方程式代入方程式(3):[3]
內部任意位置的電勢。將上述方程式代入方程式(3):[3]![\begin{align}\phi(\mathbf{r}) & =\frac{2z}{4 \pi}\left\{\int_{0+}^{\infty}\int_{-\infty}^{\infty}\cfrac{V \mathrm{d}x'\mathrm{d}y'
}{[(x-x')^2+(y-y')^2+ z^2]^{3/2}}+\int_{-\infty}^{0-}\int_{-\infty}^{\infty}\cfrac{-V \mathrm{d}x'\mathrm{d}y'
}{[(x-x')^2+(y-y')^2+ z^2]^{3/2}}\right\} \\
& =\ \frac{zV}{\pi}\left\{\int_{0+}^{\infty}\frac{\mathrm{d}y'}{(y-y')^2+ z^2}
-\int_{-\infty}^{0-} \frac{\mathrm{d}y'}{(y-y')^2+ z^2}\right\} \\
& =\frac{2V}{\pi}\ \arctan{\left(\frac{y}{z}\right)} \\
\end{align}](http://upload.wikimedia.org/math/9/1/f/91f490aaadbdeaa9a6cbe189d2fae818.png) 。
。
[编辑] 推廣至電動力學
假設磁場相依於時間(每當電場相依於時間,則此假設成立。逆過來亦成立),則不能簡單地以純量勢 描述電場。因為 根據法拉第電磁感應定律,
描述電場。因為 根據法拉第電磁感應定律,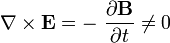 ,電場不再具有保守性,
,電場不再具有保守性, 相依於路徑。
相依於路徑。替代地,在定義純量勢時,必須引入磁向量勢
 ,定義為
,定義為 ;
;
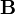 是磁場。
是磁場。根據亥姆霍茲定理[5] (Helmholtz theorem) ,假設一個向量函數
 滿足以下兩條件:
滿足以下兩條件: 、
、 ;
;
 是個純量函數,
是個純量函數, 是個向量函數。
是個向量函數。再假設
 和
和  ,在無窮遠處都足夠快速地趨向 0 ,則
,在無窮遠處都足夠快速地趨向 0 ,則  可以用方程式表達為
可以用方程式表達為 ;
;
 只作用於
只作用於  ,體積分的體積為
,體積分的體積為 。
。採用庫侖規範 (Coulomb gauge) ,則磁向量勢
 遵守
遵守 。
。
 。
。
 ,結果也成立。所以,永遠可以找到磁向量勢
,結果也成立。所以,永遠可以找到磁向量勢  :
: 。
。
 是一個保守場:
是一個保守場: 。
。
 ,滿足
,滿足  。因此,下述方程式成立:
。因此,下述方程式成立: 。
。
 不相依於時間。從另一方面來說,對於含時向量場,電場的路徑積分與靜電學的結果大不相同:
不相依於時間。從另一方面來說,對於含時向量場,電場的路徑積分與靜電學的結果大不相同: 。
。
[编辑] 參閱
[编辑] 參考文獻
2010年,理论物理学界有重大发现。荷兰人艾瑞·威林德(Erik Verlinde)提出“引力能解释为熵力”,引发弦论研究者的大讨论。中科院理论物理研究所研究员李淼对Erik的理论进行了完善,修正了其中一个重要错误。这个理论的意义何在?破绽在哪里?我国的理论物理学家在这方面又有哪些最新发现?带着这些问题,记者在近期举办的一次“果壳时间”科普讲座之后,采访了与会嘉宾——理论物理学家李淼。
引力是否为熵力
(余惠敏)问:过去的一年里,荷兰人艾瑞·威林德(Erik Verlinde)的引力即熵力理论在理论物理学界引起了很大反响,这个理论有什么不凡之处?
(李水)答:威林德2010年1月提出万有引力就是熵力的想法。牛顿认为,引力是无条件的万有引力,是基本力。爱因斯坦的时空理论中,万有引力是时空弯曲引起的,但他仍然认为万有引力是基本力。而在威林德的熵力理论中,即使时空弯曲也是熵变引起的。他认为,引力本身不是基本的作用力,而是一种宏观力,叫做熵力。这种观点目前很流行,同时也有一定的争议。
问:熵力是什么力?
答:熵在物理学中指的是混乱度,混乱度增大,熵增加。熵力的一个例子是耳机线,我们将耳机线整理好放进口袋,下次再拿出来已经乱了。让耳机线乱掉的看不见的“力”就是熵力,耳机线喜欢变成更混乱。熵力另一个具体的例子是弹性力。一根弹簧的力,就是熵力,
熵力:认识宇宙的新视角
作者:余惠敏 来源:网络 更新日期:2012-02-17 浏览次数:
11401次



 表示;而其大小則用
表示;而其大小則用  來表示。
來表示。

 。
。
No comments:
Post a Comment