單演系統[编辑]
维基百科,自由的百科全书
在經典力學裏,單演系統(monogenic system)是最常使用的物理系統之一。這是因為單演系統提供了一個非常理想的系統,使得物理學家能夠發展與檢查嶄新的構想與理論。單演系統具有優良的數學性質,非常適合作數學分析,是任何物理理論研究的起始點。
假若在一個物理系統裏,除了約束力以外,所有的作用力都是純量廣義位勢函數的導數,而此廣義位勢函數的參數是廣義坐標,廣義速度,或時間,則稱此系統為單演系統。
在單演系統裏,除了約束力以外,所有的廣義力 與廣義位勢
與廣義位勢  的關係式可以表達為
的關係式可以表達為
 是廣義坐標,
是廣義坐標, 是廣義速度,
是廣義速度,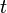 是時間。
是時間。
假若在一個物理系統裏,除了約束力以外,所有的作用力都是純量廣義位勢函數的導數,而此廣義位勢函數的參數是廣義坐標,廣義速度,或時間,則稱此系統為單演系統。
在單演系統裏,除了約束力以外,所有的廣義力
 與廣義位勢
與廣義位勢  的關係式可以表達為
的關係式可以表達為 ;
;
 是廣義坐標,
是廣義坐標, 是廣義速度,
是廣義速度,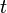 是時間。
是時間。- 假若一個單演系統的廣義位勢只跟廣義坐標有關,則此系統是保守系統。廣義力與廣義位勢的關係是
-
 ;
;
No comments:
Post a Comment