指数函数[编辑]
维基百科,自由的百科全书

指数函数对于 x 的负数值非常平坦,对于 x 的正数值迅速攀升,在 x 等于 0 的时候等于 1。它的 y 值总是等于在这一点上的斜率。
作为实数变量 x 的函数,y=ex 的图像总是正的(在 x 轴之上)并递增(从左向右看)。它永不触及 x 轴,尽管它可以任意程度的靠近它(所以,x 轴是这个图像的水平渐近线。它的反函数是自然对数 ln(x),它定义在所有正数 x 上。
有时,特别是在科学中,术语指数函数更一般性的用于形如 kax 的函数,这里的 a 叫做“底数”,是不等于 1 的任何正实数。本文最初集中于带有底数为欧拉数 e 的指数函数。
一般的说,变量 x 可以是任何实数或复数,甚至是完全不同种类的数学对象;参见后面的形式定义。
目录
[隐藏]性质[编辑]
最简单的,指数函数按恒定速率翻倍。例如细菌培养时细菌总数(近似的)每三个小时翻倍,和汽车的价值每年减少 10% 都可以被表示为一个指数。使用自然对数,你可以定义更一般的指数函数。函数
 的定义依赖于先前确立的定义于所有实数上的函数
的定义依赖于先前确立的定义于所有实数上的函数 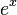 的存在。(这里我们先既不在形式上的也不概念上明确这样一个函数是否存在,或非自然指数意味着什么。)
的存在。(这里我们先既不在形式上的也不概念上明确这样一个函数是否存在,或非自然指数意味着什么。)注意上述等式对于 a = e 成立,因为
导数和微分方程[编辑]
指数函数在数学和科学中的重要性主要源于它的导数的性质。特别是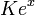 的函数是唯一有这个性质的函数。(这得出自皮卡-林德洛夫定理,通过
的函数是唯一有这个性质的函数。(这得出自皮卡-林德洛夫定理,通过 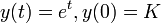 和
和 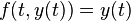 )。其他等价说法有:
)。其他等价说法有:事实上,很多不同的方程引发指数函数,包括薛定谔方程和拉普拉斯方程和简单谐波运动的方程。
对于有其他底数的指数函数:
如果一个变量的增长或衰减速率是与它的大小成比例的,比如在无限制情况下的人口增长、复利和放射性衰变,则这个变量可以写为常数倍的时间的指数函数。
进一步的,对任何可微函数 f(x),我们可以通过链式法则找到:
 .
.
形式定义[编辑]
指数函数 ex 可以用各种等价的无穷级数的方式定义。特别是它可以定义为幂级数:这些定义的进一步解释和它们的等价性的证明,参见文章指数函数的特征描述。
数值值[编辑]
要得到指数函数的数值值,无穷级数可以重写为:为了确保如此,我们可以使用下列恒等式。
- 这里的
 是
是  的整数部分
的整数部分 - 这里的
 是
是  的小数部分
的小数部分 - 所以,
 总是小于 1 而
总是小于 1 而  和
和  合计为
合计为  。
。
计算实数 x 的 exp(x)[编辑]
可以找到如下更好的算法。首先,注意到答案 y = ex 通常是用尾数 m 和指数 n 表示的浮点数,所以 y = m 2n 对于某个整数 n 和适合的小 m。因此我们得到了:
ex 的连分数[编辑]
通过欧拉恒等式:计算自然数(正整数) n 的 an 的算法[编辑]
最快的方式计算 ,当 n 是正整数的时候。它利用了测试一个数是奇数在计算机上是非常容易的,和通过简单的移所有位向右来除以 2 的事实。
,当 n 是正整数的时候。它利用了测试一个数是奇数在计算机上是非常容易的,和通过简单的移所有位向右来除以 2 的事实。偽代碼:
1. 1 → y, n → k, a → f
2. 若k不為0, 執行3至6
3. 若k為奇數, y * f → y
4. k 右移 1位 (即 k / 2 → k ,小數點無條件捨去)
5. f * f → f
6. 回到2
7. 傳回y
在C++语言中,你可以写如下算法:double power(double a, unsigned int n) { double y = 1; double f = a; unsigned int k = n; while (k != 0) { if (k % 2 == 1) y *= f; k >>= 1; f *= f; } return y; }
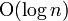 比普通算法快(a 自乘100次,多項式時間為
比普通算法快(a 自乘100次,多項式時間為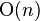 ),在n 較大的時候更為顯著
),在n 較大的時候更為顯著例如 計算
 ,普通算法需要算100次,上述算法則只需要算7次
,普通算法需要算100次,上述算法則只需要算7次若要計算
 可先以上述算法計算
可先以上述算法計算 ,再作倒數
,再作倒數在複平面上[编辑]
在考虑定义在複平面上的函数的时候,指数函数拥有重要的性质它是周期的全纯函数,带有虚数周期
 ,它可以写为
,它可以写为参见欧拉公式。
扩展自然对数到复数参数生成多值函数 ln(z)。我们可以接着定义更一般性的指数函数:
指数函数把在複平面上任何直线映射到在複平面中以原点为中心的对数螺线。要注意两个特殊情况: 当最初的线平行于实轴的时候,结果的螺线永不遮盖(close in on)自身;当最初的线平行于虚轴的时候,结果的螺线是某个半径的圆。
- 在複平面上指数函数(主支)
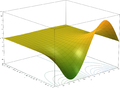
计算复数 z 的 exp(z)[编辑]
非常直接的给出公式计算复数 a 和 b 的 ab[编辑]
直接给出公式:如果 a = x + yi 且 b = u + vi,先把 a 转换到极坐标,需要找到满足如下条件的
 和
和  :
: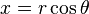 且
且 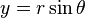
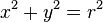 或
或  而且
而且  或
或  。
。现在我们有:

 ,
,  和
和  都是实数值。
都是实数值。 的结果因此是
的结果因此是  。
。还要注意因为我们计算和使用了
 而不是 r 自身,你不需要计算平方根。转而简单的计算
而不是 r 自身,你不需要计算平方根。转而简单的计算 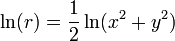 。预防潜在的上溢出并尽可能在计算
。预防潜在的上溢出并尽可能在计算 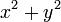 之前通过适当的 2 幂按比例缩减 x 和 y,如果
之前通过适当的 2 幂按比例缩减 x 和 y,如果  和
和  太大就会上溢出。如果你有下溢出的危险,在计算平方和之前通过适当的 2 的幂按比例增加它们。在任何一个情况下,你可以接着得到按比例缩放版本的
太大就会上溢出。如果你有下溢出的危险,在计算平方和之前通过适当的 2 的幂按比例增加它们。在任何一个情况下,你可以接着得到按比例缩放版本的  称为
称为 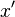 ,和按比例缩放版本的
,和按比例缩放版本的  称为
称为  ,因此得到:
,因此得到: 和
和 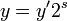
 是缩放因子。
是缩放因子。接着得到
 这里的
这里的 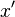 和
和  被缩放了使得平方和不上溢出或下溢出。如果
被缩放了使得平方和不上溢出或下溢出。如果  是非常大而
是非常大而  是非常小,因而不能找到这样一个缩放因子,你就会上溢出所以这个和本质上等于
是非常小,因而不能找到这样一个缩放因子,你就会上溢出所以这个和本质上等于  ,因为 y 被忽略了,因此你在这种情况下得到了
,因为 y 被忽略了,因此你在这种情况下得到了  和
和  。同样情况出现在
。同样情况出现在  非常小而
非常小而  非常大的时候。如果两个都非常小或都非常大就可以找到前面提到的缩放因子。
非常大的时候。如果两个都非常小或都非常大就可以找到前面提到的缩放因子。矩阵和巴拿赫代数[编辑]
上面给出的指数函数的定义可以用于所有巴拿赫代数,特别是对于方块矩阵(在这种情况函数叫做矩阵指数)。在这种情况下我们有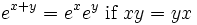
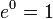
 与
与 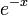 是互倒的
是互倒的 在点
在点  的导数是从
的导数是从 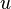 到
到  的线性映射。
的线性映射。

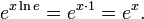
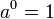
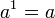
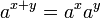
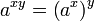

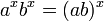
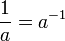
![\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}.](http://upload.wikimedia.org/math/8/2/1/821704e8992ee67a4d8988774e23bcb8.png)
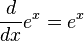
 的解。
的解。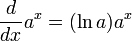

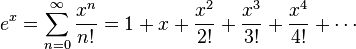





![= e^z \times \left[{1 \over 0!} + f \, \left( {1 \over 1!} + f \, \left( {1 \over 2!} + f \, \left( {1 \over 3!} + \cdots \right)\right)\right)\right]](http://upload.wikimedia.org/math/8/8/a/88ac816fd09958f9f2f59456577efe71.png)

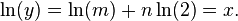
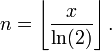
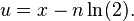






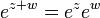

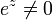

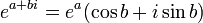









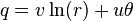



No comments:
Post a Comment