Everett的日记
从涡旋到电与光的演生
2013-04-30 21:10:10
(一)经典涡旋的动力学
涡旋是一种在流体中常见的运动形式,它指的是在一定范围内流体围绕涡旋中心做持续性的旋转流动。涡旋广泛地出现在各种尺度上,包括木星上的气旋和咖啡杯里的漩涡。
由于涡旋可以在流体中维持一段时间,我们可以把它看成一种有限寿命的粒子。我们可以在咖啡杯里制造涡旋:用匙子在杯中划过,往往就会在尾流上激发两个反向旋转的涡旋。如果找一个闲暇的下午,坐在咖啡厅里观察一下涡旋的世界,就会发现以下一些有趣的物理:(1) 涡旋按照其旋转方向可以分为正涡旋(逆时针旋转)和负涡旋(顺时针旋转)两种,就好像两种电量相反的电荷一样。 (2) 一个孤立的涡旋总是随着背景流体一起流动,没有惯性。也就是说,涡旋是无质量的。(3) 一对反向旋转的涡旋总是束缚在一起平行运动(比如匙子后面的两个涡旋会一起脱离匙子,并顺着尾流运动)。 正负涡旋可以互相湮灭,并释放旋转的能量(一般是通过粘滞耗散掉了)。这种行为有点类似于正反夸克构成介子,夸克湮灭以后,介子可以衰变成光(释放能量)。
涡旋的这些特点暗示我们可以把涡旋类比为某种携带“电荷”的无质量粒子。这里所谓的电荷,就是涡旋量[;\Gamma;],它衡量涡旋的旋转程度的大小,并正比于流速场[;u;]在包围涡旋的环路上的线积分[;\Gamma=\oint u\cdot\mathrm{d}l;]。这个定义与静电学中电荷的高斯定理非常相似,都明显地带有拓扑的风格:也就是说环路可以形变,但只要不扫过涡旋,涡旋量就不会有差别。 这种拓扑的定义也表明涡旋也是全局的概念:尽管涡旋的中心可以看成点状的粒子,但涡旋的意义却蕴于中心以外环流的完整样式之中。
如果说涡旋是一种演生的电荷,那么涡旋之间是否也像电荷一样同性相斥、异性相吸呢?答案是肯定的,同号涡旋之间确实存在类似于静电作用的斥力,而相反涡旋之间则表现为引力。这个演生的静电作用源于流体的Bernoulli原理:同一条流线上,流速大的地方压强小。
对于一对同号的涡旋,流速大的地方在涡旋的外侧,因此受到的压力向外;而对于一对异号的涡旋,流速大的部分在涡旋之间,因此受到的压力向内。只不过涡旋之间的这种静电力并不遵从我们熟知的平方反比律,而是遵循一次方反比律[;F_E\propto\Gamma_1\Gamma_2/r_{12};]。这是二维与三维世界的一个重要差别。因为涡旋生活在二维的世界里,演生的电场线也只能在两个空间维度上散开,这样电场强度就不会衰减得像在三维空间中那么快,结果就得到一次方反比的静电作用。因此,我们看到涡旋不但可以看作演生的电荷,而且它们之间的相互作用也满足二维世界的Coulomb定律。
如果两个相反涡旋之间具有所谓的静电吸引,那么它们为什么不像双星一样相互绕转呢?这是因为除了演生的电力[;F_E;],涡旋还受到演生的磁力[;F_B;]。也就是说,当涡旋在流体中运动的时候,会受到垂直于运动方向的偏转力。它的起源与香蕉球的原理相同(旋转的球周围也存在涡旋,从而导致球的轨迹偏离直线),其效果就像电荷在均匀磁场中运动会受到Lorentz力[;F_B=v\times B;]一样。所以对于涡旋来说,流体背景就像一个均匀的磁场一样,其磁场强度正比于流体的密度。当作用在涡旋上的演生电场力和演生磁场力平衡的时候,就出现了我们看到了咖啡杯里一对相反涡旋在一起平行运动的现象(见上文图中的受力分析)。
我们看到电场和磁场都出现了,那么会出现电磁波吗?答案仍然是肯定的。如果把涡旋视为演生的电荷,那么演生的电磁波就是流体中的声波(密度波)。可以证明在二维空间中,电磁波的Maxwell方程与声波的Euler方程在形式上是完全对偶的。电动力学中的电磁感应就等价于流体力学中的流守恒方程:电磁波中电场和磁场交互激发的过程,相当于是流体中流动导致密度积累,而密度积累又驱动新的流动这样的过程。综上所述,我们可以建立如下类比关系:
涡旋动力学 = 电动力学
涡旋 = 电荷
流体密度 = 磁场
流体速度 = 电场
声波 = 电磁波
通过以上的讨论,我们显示了(二维空间内)涡旋在流体中的行为就像电荷在电磁场中的行为一样。涡旋其实就是电荷演生的一种最简单的模型,而流体扮演的角色就像人们曾经构想的以太一样:光的媒介。
(二)量子流体与量子涡旋
现在,我们需要从经典走向量子。因为在现实世界中,电荷往往是量子化的,也就是说存在最小的单位电荷(比如电子电荷)。为了从涡旋的角度来理解这件事情,我们需要涉及一点点量子力学。量子力学的基本原理就是波粒二象性:波动可以视作粒子,而粒子都有波动的行为。这里的波动是一种波函数相位随空间变化的运动形式,而量子力学将这种相位的变化与粒子的动量联系在一起:动量 = 平移单位距离所积累的相位。而对于构成流体微观自由度来说,它们的速度与动量成比例,因此也就与相位的空间梯度成比例,可以表达为[;u\propto \nabla\theta/2\pi;]。也就是说,在量子流体中,每个涡旋的背后实际上是一个围绕涡旋中心旋转而改变的相位分布。
由于波函数的单值性(也就是说一个点只能有唯一确定的波函数取值),这就要求流体环绕一周以后相位只能相差[;2\pi;]的整数倍(因为[;2\pi;]表示相位转过一周,波函数恢复原来的取值),也就是说涡旋量只能是一个基本单位的整数倍。这个最小单位就是环绕一圈相位改变一周的涡旋,称为量子涡旋。量子涡旋是量子流体波函数的拓扑奇异点,围绕这些奇异点,波函数的相位将有一个周期的改变。在量子流体中,涡旋只能一个一个单位地激发,而比量子涡旋更小的涡旋将导致波函数的出现割线而不被量子力学所允许。按照我们之前所做的类比,涡旋量代表演生的电荷量,那么量子涡旋就提供了关于电荷量子化的一种自然的理解:如果涡旋必须一个一个激发,那么电荷也是一样的。这就在某种程度上解释了电荷存在基本单位的量子力学原因(至少对二维空间的情形而言)。
量子涡旋的中心是由整个背景的相位分布的图样决定的,也就是说关于涡旋在哪里的信息实际上是散布在整个量子流体的背景中的。这是一个令人惊讶的观念,也就是说粒子的定义不来自于自身而来自于整个真空的集体作用。在还原论的观念中,真空是舞台,粒子才是舞台上的主角;而在演生论的观念看来,真空不但积极地参与了粒子建构,而且实际上操纵着粒子的行为。而粒子本身的意义反而变得模糊,或者说粒子只是作为真空的运动模式的物化体现。而这种运动模式的具体规律则由真空的序(组织方式)决定,这也就是凝聚态物理的核心观念:序决定激发,真空决定粒子。
(三)奇异弦与弦网凝聚
为了更加明确地看出量子涡旋的非局域本质,我们需要提取量子流体相位分布背后所隐含的结构。下图显示了包含有许多量子涡旋的相位分布,其中以+/-标记涡旋的符号。
我们将所有的零相位线标出,并且以箭头标明方向(从正涡旋发出而收于负涡旋)。可以看到这些线总是连接一对正负涡旋(或者延伸到无限远去),它们就是量子涡旋之间看不见的奇异弦。在奇异弦的刻画下,原先光怪陆离的相位分布背后的结构立刻变得清晰明了: 每次跨过奇异弦,相位就变化一周,至于是增加还是减少取决于奇异弦的方向与跨越方向之间是右手还是左手关系。在这个图像下,量子涡旋获得了一个更加深刻的含义:它们是奇异弦的末端! 隐藏在相位结构中的奇异弦明确地表达出了涡旋的非局域本质:它们是量子流体的拓扑激发。
将粒子理解为开弦的末端,这种思路始于超弦理论,并且产生了深远的影响:物理学不再局限于对点状对象(粒子)的研究,而是拓展到了线、面等更加高维的延展几何对象(比如弦、膜等)。而从量子涡旋到奇异弦的这一拓展并不仅仅是理论家的一种数学游戏,它代表了从“面向对象”的物理学到“面向关系”的物理学这样一种风格上的转变。在面向对象的物理学中,我们关注的是流体中看得见的一个个涡旋;而在面向关系的物理学中,我们强调的是涡旋之间的一种看不见的关系(奇异弦),而且更进一步,我们甚至可以而且应该用这个关系来定义涡旋。也就是说,涡旋是作为奇异弦的末端存在的!是奇异弦的关系定义了涡旋的意义。
对于由涡旋演生电荷来说,奇异弦就相当于演生的电场线:电荷是作为电场线的末端而存在的。量子化的电场线就给出量子化的电荷。这些电场线在量子涨落的作用下,不断地在空间中扭动变形,而且真空中也充满了涨落的电场线闭弦,这种状态被称为弦网凝聚,对应于我们熟知的解禁闭的电动力学。涨落的电场线同时也传递了电荷之间的相互作用,这等价于在量子场论中由光子传递的电磁相互作用,因此电场线的涨落模式就是演生的光子。研究还表明,电荷的费米统计也可以由弦网凝聚自然地给出,从而得到演生的电子。如果假定我们的真空是弦网凝聚体,那么电子的光子就有一种很简单的图像:光子是弦的震荡,而电子则是弦的末端。这样看来,宇宙的图景就像一锅巨大的面汤一样充满了流动的面条。我想飞面神教的信众们也许会很欣赏这样的看法。
量子电动力学与(量子)弦论的这种等价关系被称为规范-弦对偶。而另一方面,某些弦论的经典动力学自然地是引力理论,就像广义相对论那样。这实际上就建立了规范理论和引力理论的一种对应关系,比如AdS/CFT对应就是一个广为人知的例子。特别是最近几年来,这种对应在凝聚态物理学领域也激起了广泛的兴趣,人们希望通过AdS空间的引力理论,来理解其边界上强耦合的规范动力学。在历史上,高能物理曾经多次与凝聚态物理携手共进,每一次都取得了辉煌的成就,比如对称自发破缺以及重整化群理论的发展,那么在今天蓬勃兴起的AdS/CFT对应会不会是他们第三次成功的合作呢?让我们拭目以待~
涡旋是一种在流体中常见的运动形式,它指的是在一定范围内流体围绕涡旋中心做持续性的旋转流动。涡旋广泛地出现在各种尺度上,包括木星上的气旋和咖啡杯里的漩涡。
 |
木星上的涡旋与咖啡杯里的涡旋
|
由于涡旋可以在流体中维持一段时间,我们可以把它看成一种有限寿命的粒子。我们可以在咖啡杯里制造涡旋:用匙子在杯中划过,往往就会在尾流上激发两个反向旋转的涡旋。如果找一个闲暇的下午,坐在咖啡厅里观察一下涡旋的世界,就会发现以下一些有趣的物理:(1) 涡旋按照其旋转方向可以分为正涡旋(逆时针旋转)和负涡旋(顺时针旋转)两种,就好像两种电量相反的电荷一样。 (2) 一个孤立的涡旋总是随着背景流体一起流动,没有惯性。也就是说,涡旋是无质量的。(3) 一对反向旋转的涡旋总是束缚在一起平行运动(比如匙子后面的两个涡旋会一起脱离匙子,并顺着尾流运动)。 正负涡旋可以互相湮灭,并释放旋转的能量(一般是通过粘滞耗散掉了)。这种行为有点类似于正反夸克构成介子,夸克湮灭以后,介子可以衰变成光(释放能量)。
 |
匙子划过激发的正负涡旋对,及其受力分析
|
涡旋的这些特点暗示我们可以把涡旋类比为某种携带“电荷”的无质量粒子。这里所谓的电荷,就是涡旋量[;\Gamma;],它衡量涡旋的旋转程度的大小,并正比于流速场[;u;]在包围涡旋的环路上的线积分[;\Gamma=\oint u\cdot\mathrm{d}l;]。这个定义与静电学中电荷的高斯定理非常相似,都明显地带有拓扑的风格:也就是说环路可以形变,但只要不扫过涡旋,涡旋量就不会有差别。 这种拓扑的定义也表明涡旋也是全局的概念:尽管涡旋的中心可以看成点状的粒子,但涡旋的意义却蕴于中心以外环流的完整样式之中。
如果说涡旋是一种演生的电荷,那么涡旋之间是否也像电荷一样同性相斥、异性相吸呢?答案是肯定的,同号涡旋之间确实存在类似于静电作用的斥力,而相反涡旋之间则表现为引力。这个演生的静电作用源于流体的Bernoulli原理:同一条流线上,流速大的地方压强小。
 |
一对涡旋附近的流场
|
对于一对同号的涡旋,流速大的地方在涡旋的外侧,因此受到的压力向外;而对于一对异号的涡旋,流速大的部分在涡旋之间,因此受到的压力向内。只不过涡旋之间的这种静电力并不遵从我们熟知的平方反比律,而是遵循一次方反比律[;F_E\propto\Gamma_1\Gamma_2/r_{12};]。这是二维与三维世界的一个重要差别。因为涡旋生活在二维的世界里,演生的电场线也只能在两个空间维度上散开,这样电场强度就不会衰减得像在三维空间中那么快,结果就得到一次方反比的静电作用。因此,我们看到涡旋不但可以看作演生的电荷,而且它们之间的相互作用也满足二维世界的Coulomb定律。
如果两个相反涡旋之间具有所谓的静电吸引,那么它们为什么不像双星一样相互绕转呢?这是因为除了演生的电力[;F_E;],涡旋还受到演生的磁力[;F_B;]。也就是说,当涡旋在流体中运动的时候,会受到垂直于运动方向的偏转力。它的起源与香蕉球的原理相同(旋转的球周围也存在涡旋,从而导致球的轨迹偏离直线),其效果就像电荷在均匀磁场中运动会受到Lorentz力[;F_B=v\times B;]一样。所以对于涡旋来说,流体背景就像一个均匀的磁场一样,其磁场强度正比于流体的密度。当作用在涡旋上的演生电场力和演生磁场力平衡的时候,就出现了我们看到了咖啡杯里一对相反涡旋在一起平行运动的现象(见上文图中的受力分析)。
我们看到电场和磁场都出现了,那么会出现电磁波吗?答案仍然是肯定的。如果把涡旋视为演生的电荷,那么演生的电磁波就是流体中的声波(密度波)。可以证明在二维空间中,电磁波的Maxwell方程与声波的Euler方程在形式上是完全对偶的。电动力学中的电磁感应就等价于流体力学中的流守恒方程:电磁波中电场和磁场交互激发的过程,相当于是流体中流动导致密度积累,而密度积累又驱动新的流动这样的过程。综上所述,我们可以建立如下类比关系:
涡旋动力学 = 电动力学
涡旋 = 电荷
流体密度 = 磁场
流体速度 = 电场
声波 = 电磁波
通过以上的讨论,我们显示了(二维空间内)涡旋在流体中的行为就像电荷在电磁场中的行为一样。涡旋其实就是电荷演生的一种最简单的模型,而流体扮演的角色就像人们曾经构想的以太一样:光的媒介。
(二)量子流体与量子涡旋
现在,我们需要从经典走向量子。因为在现实世界中,电荷往往是量子化的,也就是说存在最小的单位电荷(比如电子电荷)。为了从涡旋的角度来理解这件事情,我们需要涉及一点点量子力学。量子力学的基本原理就是波粒二象性:波动可以视作粒子,而粒子都有波动的行为。这里的波动是一种波函数相位随空间变化的运动形式,而量子力学将这种相位的变化与粒子的动量联系在一起:动量 = 平移单位距离所积累的相位。而对于构成流体微观自由度来说,它们的速度与动量成比例,因此也就与相位的空间梯度成比例,可以表达为[;u\propto \nabla\theta/2\pi;]。也就是说,在量子流体中,每个涡旋的背后实际上是一个围绕涡旋中心旋转而改变的相位分布。
 |
不同的颜色代表不同的相位,量子流体的流速与相位的梯度成正比
|
由于波函数的单值性(也就是说一个点只能有唯一确定的波函数取值),这就要求流体环绕一周以后相位只能相差[;2\pi;]的整数倍(因为[;2\pi;]表示相位转过一周,波函数恢复原来的取值),也就是说涡旋量只能是一个基本单位的整数倍。这个最小单位就是环绕一圈相位改变一周的涡旋,称为量子涡旋。量子涡旋是量子流体波函数的拓扑奇异点,围绕这些奇异点,波函数的相位将有一个周期的改变。在量子流体中,涡旋只能一个一个单位地激发,而比量子涡旋更小的涡旋将导致波函数的出现割线而不被量子力学所允许。按照我们之前所做的类比,涡旋量代表演生的电荷量,那么量子涡旋就提供了关于电荷量子化的一种自然的理解:如果涡旋必须一个一个激发,那么电荷也是一样的。这就在某种程度上解释了电荷存在基本单位的量子力学原因(至少对二维空间的情形而言)。
量子涡旋的中心是由整个背景的相位分布的图样决定的,也就是说关于涡旋在哪里的信息实际上是散布在整个量子流体的背景中的。这是一个令人惊讶的观念,也就是说粒子的定义不来自于自身而来自于整个真空的集体作用。在还原论的观念中,真空是舞台,粒子才是舞台上的主角;而在演生论的观念看来,真空不但积极地参与了粒子建构,而且实际上操纵着粒子的行为。而粒子本身的意义反而变得模糊,或者说粒子只是作为真空的运动模式的物化体现。而这种运动模式的具体规律则由真空的序(组织方式)决定,这也就是凝聚态物理的核心观念:序决定激发,真空决定粒子。
(三)奇异弦与弦网凝聚
为了更加明确地看出量子涡旋的非局域本质,我们需要提取量子流体相位分布背后所隐含的结构。下图显示了包含有许多量子涡旋的相位分布,其中以+/-标记涡旋的符号。
 |
我们将所有的零相位线标出,并且以箭头标明方向(从正涡旋发出而收于负涡旋)。可以看到这些线总是连接一对正负涡旋(或者延伸到无限远去),它们就是量子涡旋之间看不见的奇异弦。在奇异弦的刻画下,原先光怪陆离的相位分布背后的结构立刻变得清晰明了: 每次跨过奇异弦,相位就变化一周,至于是增加还是减少取决于奇异弦的方向与跨越方向之间是右手还是左手关系。在这个图像下,量子涡旋获得了一个更加深刻的含义:它们是奇异弦的末端! 隐藏在相位结构中的奇异弦明确地表达出了涡旋的非局域本质:它们是量子流体的拓扑激发。
将粒子理解为开弦的末端,这种思路始于超弦理论,并且产生了深远的影响:物理学不再局限于对点状对象(粒子)的研究,而是拓展到了线、面等更加高维的延展几何对象(比如弦、膜等)。而从量子涡旋到奇异弦的这一拓展并不仅仅是理论家的一种数学游戏,它代表了从“面向对象”的物理学到“面向关系”的物理学这样一种风格上的转变。在面向对象的物理学中,我们关注的是流体中看得见的一个个涡旋;而在面向关系的物理学中,我们强调的是涡旋之间的一种看不见的关系(奇异弦),而且更进一步,我们甚至可以而且应该用这个关系来定义涡旋。也就是说,涡旋是作为奇异弦的末端存在的!是奇异弦的关系定义了涡旋的意义。
对于由涡旋演生电荷来说,奇异弦就相当于演生的电场线:电荷是作为电场线的末端而存在的。量子化的电场线就给出量子化的电荷。这些电场线在量子涨落的作用下,不断地在空间中扭动变形,而且真空中也充满了涨落的电场线闭弦,这种状态被称为弦网凝聚,对应于我们熟知的解禁闭的电动力学。涨落的电场线同时也传递了电荷之间的相互作用,这等价于在量子场论中由光子传递的电磁相互作用,因此电场线的涨落模式就是演生的光子。研究还表明,电荷的费米统计也可以由弦网凝聚自然地给出,从而得到演生的电子。如果假定我们的真空是弦网凝聚体,那么电子的光子就有一种很简单的图像:光子是弦的震荡,而电子则是弦的末端。这样看来,宇宙的图景就像一锅巨大的面汤一样充满了流动的面条。我想飞面神教的信众们也许会很欣赏这样的看法。
量子电动力学与(量子)弦论的这种等价关系被称为规范-弦对偶。而另一方面,某些弦论的经典动力学自然地是引力理论,就像广义相对论那样。这实际上就建立了规范理论和引力理论的一种对应关系,比如AdS/CFT对应就是一个广为人知的例子。特别是最近几年来,这种对应在凝聚态物理学领域也激起了广泛的兴趣,人们希望通过AdS空间的引力理论,来理解其边界上强耦合的规范动力学。在历史上,高能物理曾经多次与凝聚态物理携手共进,每一次都取得了辉煌的成就,比如对称自发破缺以及重整化群理论的发展,那么在今天蓬勃兴起的AdS/CFT对应会不会是他们第三次成功的合作呢?让我们拭目以待~







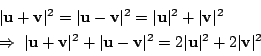
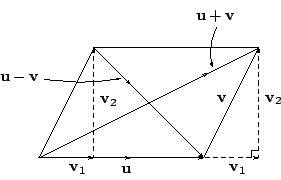
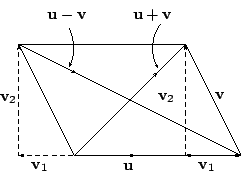
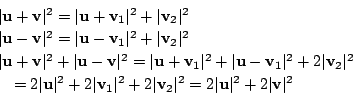
![\begin{displaymath}
\xy
\xyimport(5,5){\epsfxsize=4cm \epsfbox{fig0504.eps}}*\fr...
...ntfamily{cwM0}\fontseries{m}\selectfont \cH199} 5--4 ]}}
\endxy\end{displaymath}](http://episte.math.ntu.edu.tw/articles/ar/ar_wy_geo_05/img174.gif)
![\begin{eqnarray*}[(0,\mathbf{a})\cdot (0,\mathbf{b})]\cdot (0,\mathbf{c}) &=& (-...
...}),\; -\mathbf{(b\cdot c)a} + \mathbf{a\times (b\times c)} \big)
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/ar/ar_wy_geo_05/img234.gif)