http://zhuanlan.zhihu.com/maths/19725035
流形- 維基百科,自由的百科全書 - Wikipedia
专题讨论: 三维球面
www.math.pku.edu.cn/teachers/baozq/topology/s3/s3.htm
轉為繁體網頁
科学网—走近三维流形:从双曲几何到立方复形的双向之旅(四 ...
blog.sciencenet.cn/blog-716301-638278.html
轉為繁體網頁
[PDF]Poincare´ 猜测漫谈 - 南京大学数学系
math.nju.edu.cn/~meijq/Poincare.pdf
轉為繁體網頁
不一样的贪吃蛇- 比生活简单多了 - 知乎专栏
zhuanlan.zhihu.com/maths/19725035
轉為繁體網頁
[PDF]基于流形的光滑曲面构造 - 软件学报
www.jos.org.cn/1000-9825/17/s64.pdf
轉為繁體網頁
無聊寫篇| Quod Erat Demonstrandum
johnmayhk.wordpress.com/2013/06/17/boring-writing-2/
不一样的贪吃蛇
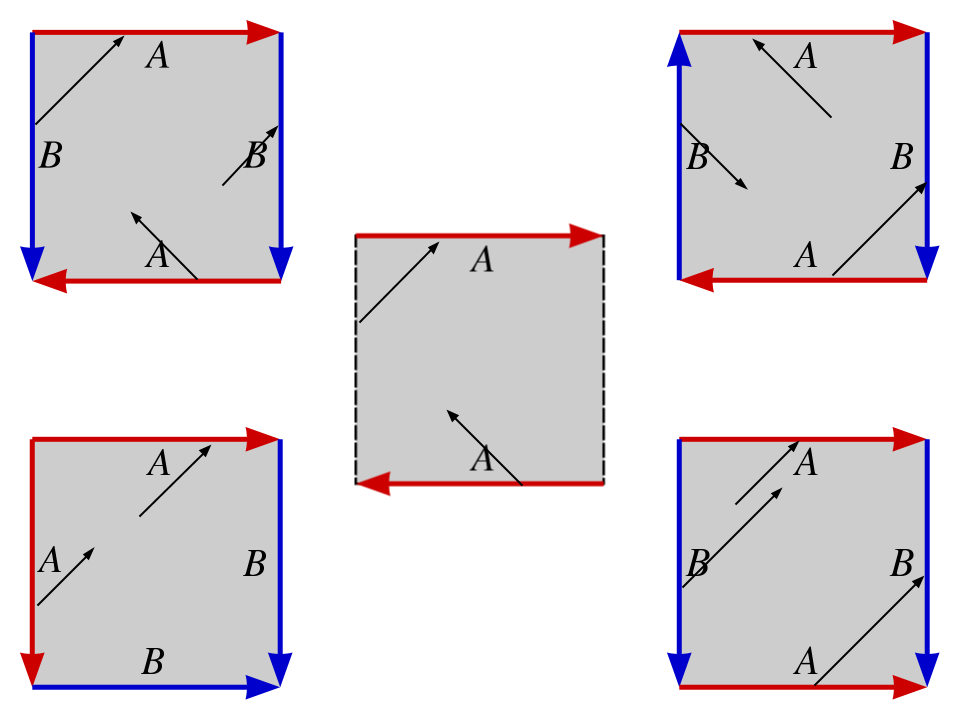 图中正方形的边界都用红色或蓝色的箭头标注,表示同色的边界按标注的方向粘合。
图中正方形的边界都用红色或蓝色的箭头标注,表示同色的边界按标注的方向粘合。先看右下角的图
设正方形左下角坐标 (0,0),右上角坐标 (1,1)。因为上下边界被粘合起来,坐标为 (x,1) 的点被等同于坐标为 (x,0) 的点。同样的,左右边界被粘合起来,所以坐标 (0,x) 的点被等同于坐标为 (1,x) 的点。
试想我所画的黑线是一个正在走直线的贪吃蛇的路径。它向右上方行进,先碰到了上边界,于是从下边界同样的横坐标处出现,继续向右上方行进,碰到右边界,然后从左边界同样的高度出现,继续向右上行进。这是大家非常熟悉的情景,有些地方叫作「周期性边界条件」。
这是什么曲面呢?很容易想象……把正方形卷成一个筒,然后再把两端接起来……没错这是一个 torus(轮胎面?甜甜圈面?)
再看左下角的图
根据标注的箭头, (0,x) 被等同于 (1-x,1),(x,0) 被等同于 (1,1-x)。这是什么曲面呢?球面。也许换个角度就更加明显了:是想一个地球,左上角是北极,右下角是南极,而 (0,0)-(1,1) 这条对角线是赤道。而左边和下面的边界,分别等同于上面和右边的边界,是「国际日期变更线」。
再看中间那幅图
根据标注的箭头,左右边界没有粘合。而上下边界,注意粘合的方向:(x,0) 被等同于 (1-x,1)。我所画的贪吃蛇,先是向右上方向行进,在偏左的地方碰到了上边界。于是他从下边界偏右的地方出现,向左上方向行进。这是什么曲面呢?注意粘合的方向是反的,是「扭」了一下再粘起来的。这正是莫比乌斯带。
现在你们知道怎么玩了,其实就是玩贪吃蛇的时候加上个变态的边界条件而已。上方的两幅图我就直接公布答案了:他们分别是克莱因瓶和射影平面。如果有人设计出这样的贪吃蛇,不知会不会流行。很有挑战不是吗?
对于数学基础不错的同学们来说,这也许太简单了。我就再贴两个当年初学时颇耗了我一些脑细胞的曲面。第一个是二维的 Dunce hat (topology):
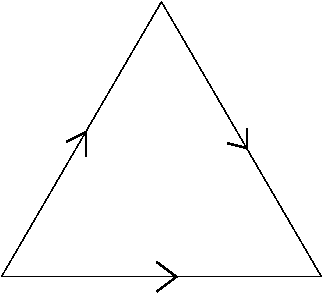 这三条边要全部按给定的方向粘合起来,三个点也因此相互等同。因此最后的结构中只有一个点,一条边,一个面。其实粘合左边和下边还是比较容易想象的,结果是一个圆锥。然后右边要怎么处理呢?想要直观可以看这个视频 https://www.youtube.com/watch?v=34j4CppfRTA 他在一块布上缝了两个拉链,做出了这个曲面。结果是一个很萌很萌的睡帽。
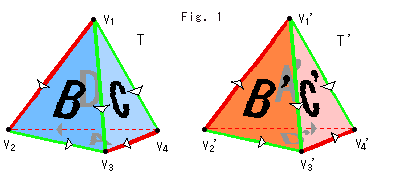
这三条边要全部按给定的方向粘合起来,三个点也因此相互等同。因此最后的结构中只有一个点,一条边,一个面。其实粘合左边和下边还是比较容易想象的,结果是一个圆锥。然后右边要怎么处理呢?想要直观可以看这个视频 https://www.youtube.com/watch?v=34j4CppfRTA 他在一块布上缝了两个拉链,做出了这个曲面。结果是一个很萌很萌的睡帽。第二个是粘合两个四面体得到的三维流形,图片来自:Figure-8 Knot (2)
No comments:
Post a Comment