(一)线性、非色散、均匀和各向同性介质_CNKI学问
xuewen.cnki.net/R2011090720000007.html
轉為繁體網頁
量子穿隧效應- 維基百科,自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hk/量子穿隧效應
馬克士威方程組- 維基百科,自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hk/馬克士威方程組
色散介质时域有限差分方法_百度百科
baike.baidu.com/view/4300829.htm
轉為繁體網頁
第4讲_麦克斯韦方程、连续方程、本构关系_百度文库
wenku.baidu.com/.../6692d00416fc700abb68fcaa.html?re...
轉為繁體網頁
[DOC]10级电磁场与电磁波复习题.doc - 武汉理工大学---网络学堂
wlxt.whut.edu.cn/new/dccydcb/.../20121122110919923.d...
轉為繁體網頁
[PDF]§1.5 介质中的麦克斯韦方程组
jpkc.fudan.edu.cn/.../2a3ee8eb-8304-4d31-9ac2-4af416a0...
轉為繁體網頁
有耗色散地质介质中的GPR脉冲传播研究 - 获取全文
book.hzu.edu.cn/824335.html - 轉為繁體網頁
有耗色散地质介质中的GPR脉冲传播研究--《成都理工大学 ...
cdmd.cnki.com.cn/Article/CDMD-10616-2008085970.htm - 轉為繁體網頁
由 李庆伟 著作 - 2008
探地雷达时域有限差分法有耗色散介质完全匹配层. ... 对有耗色散介质中的麦克斯韦计算电磁学要论(豆瓣) - 豆瓣读书
book.douban.com/subject/3350134/
轉為繁體網頁
對於實際物質,本構關係並不是簡單的線性關係,而是只能近似為簡單的線性關係。從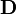 場與
場與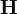 場的定義式開始,要找到本構關係式,必需先知道電極化強度和磁化強度是怎樣從電場和磁場產生的。這可能是由實驗得到(建立於直接測量),或由推論得到(建立於統計力學、傳輸力學(transport phenomena)或其它凝聚態物理學的理論)。所涉及的細節可能是宏观或微觀的。這都要視問題的層級而定。
場的定義式開始,要找到本構關係式,必需先知道電極化強度和磁化強度是怎樣從電場和磁場產生的。這可能是由實驗得到(建立於直接測量),或由推論得到(建立於統計力學、傳輸力學(transport phenomena)或其它凝聚態物理學的理論)。所涉及的細節可能是宏观或微觀的。這都要視問題的層級而定。
雖然如此,本構關係式通常仍舊可以寫為
 和
和 不再是簡單常數,而是函數。例如,
不再是簡單常數,而是函數。例如,
隨著材料科學的進步,材料專家可以設計出具有特定的電容率或磁導率的新材料,像光子晶體。
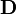 場與
場與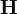 場的定義式開始,要找到本構關係式,必需先知道電極化強度和磁化強度是怎樣從電場和磁場產生的。這可能是由實驗得到(建立於直接測量),或由推論得到(建立於統計力學、傳輸力學(transport phenomena)或其它凝聚態物理學的理論)。所涉及的細節可能是宏观或微觀的。這都要視問題的層級而定。
場的定義式開始,要找到本構關係式,必需先知道電極化強度和磁化強度是怎樣從電場和磁場產生的。這可能是由實驗得到(建立於直接測量),或由推論得到(建立於統計力學、傳輸力學(transport phenomena)或其它凝聚態物理學的理論)。所涉及的細節可能是宏观或微觀的。這都要視問題的層級而定。雖然如此,本構關係式通常仍舊可以寫為
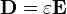 、
、 。
。
 和
和 不再是簡單常數,而是函數。例如,
不再是簡單常數,而是函數。例如,- 色散或吸收:
 和
和 是頻率的函數。因果論不允許物質具有非色散性,例如,克拉莫-克若尼關係式。場與場之間的相位可能不同相,這導致
是頻率的函數。因果論不允許物質具有非色散性,例如,克拉莫-克若尼關係式。場與場之間的相位可能不同相,這導致 和
和 為複值,也導致電磁波被物質吸收[20]。
為複值,也導致電磁波被物質吸收[20]。 - 非線性:
 和
和 都是電場與磁場的函數。例如,克爾效應[21]和波克斯效應(Pockels effect)。
都是電場與磁場的函數。例如,克爾效應[21]和波克斯效應(Pockels effect)。 - 各向異性:例如,雙折射或二向色性(dichroism)。
 和
和 都是二階張量[22]:
都是二階張量[22]:
-
 、
、 。
。
-
 、
、 ;
;
- 其中,
 與
與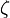 是耦合常數,每一種介質的内禀常數。
是耦合常數,每一種介質的内禀常數。
- 在雙耦合各向異性物質裏,
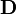 場與
場與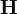 場分別各向異性地耦合於
場分別各向異性地耦合於 場與
場與 場,係數
場,係數 、
、 、
、 、
、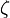 都是張量。
都是張量。
- 在不同位置和時間,
 場與
場與 場分別跟
場分別跟 場、
場、 場有關:這可能是因為「空間不勻性」。例如,一個磁鐵的域結構、異質結構或液晶,或最常出現的狀況是多種材料占有不同空間區域。這也可能是因為隨時間而改變的物質或磁滯現象。對於這種狀況,
場有關:這可能是因為「空間不勻性」。例如,一個磁鐵的域結構、異質結構或液晶,或最常出現的狀況是多種材料占有不同空間區域。這也可能是因為隨時間而改變的物質或磁滯現象。對於這種狀況, 場與
場與 場計算為[23][24]
場計算為[23][24]
-
 、
、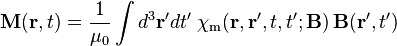 ;
;
隨著材料科學的進步,材料專家可以設計出具有特定的電容率或磁導率的新材料,像光子晶體。
 是
是 是
是
No comments:
Post a Comment