相对论理论中一个事件是在四维时空内的坐标描述的,一个物体在时空中运动产生的轨迹曲线是通过固有时这个参数实现参数化的,而这条曲线称作世界线。四维速度是一维时间与三维空间坐标对固有时的改变率所构成的矢量,同时也是世界线的切向矢量。
作为比较,在经典力学中事件是通过它们在每一时刻上在三维空间中的坐标描述的,它们在三维空间中的轨迹是通过时间这个参数实现参数化的。经典速度是三维空间坐标对时间的改变率所构成的矢量,同时也是轨迹的切向矢量。
在狭义相对论的框架中,四维速度的大小(模)总是和光速的大小相等。
经典力学的情形[编辑]
在经典力学中一个物体在三维空间中的运动路径由其在三维空间中的坐标函数 决定,这些坐标函数都是绝对时间
决定,这些坐标函数都是绝对时间 的函数:
的函数: 表示的是在
表示的是在 时刻的三个空间位置。
时刻的三个空间位置。在任意一点
 ,经典速度
,经典速度 (此点处的切线方向)的分量为
(此点处的切线方向)的分量为 点处定义的,因而它们实际是两个毗邻位置间的距离
点处定义的,因而它们实际是两个毗邻位置间的距离 对对应时间间隔
对对应时间间隔 的比值。
的比值。相对论理论[编辑]
在爱因斯坦的相对论理论中,一个物体对某个特定参考系的运动轨迹是由四维坐标函数 (其中
(其中 表示时间坐标乘以光速c)决定的,每个函数都依赖于固有时
表示时间坐标乘以光速c)决定的,每个函数都依赖于固有时 。
。时间膨胀[编辑]
从时间膨胀中我们得知 是洛伦兹因子,定义为
是洛伦兹因子,定义为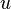 是经典速度矢量的欧几里德模:
是经典速度矢量的欧几里德模: .
.
四维速度的定义[编辑]
一个四维速度是对应世界线的四维切向矢量,四维速度的世界线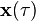 定义为
定义为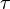 是固有时。
是固有时。四维速度的分量[编辑]
时间 和坐标
和坐标 间的关系为
间的关系为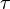 求导数,我们得到四维速度
求导数,我们得到四维速度 在
在 方向上分量为
方向上分量为 1, 2, 3,我们有
1, 2, 3,我们有 :
:四维速度和加速度[编辑]
四维加速度定义为四维速度對原时间的微分: 为常數,所以它微分为0:
为常數,所以它微分为0:注释[编辑]
在一个静止参考系中,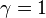 并且
并且 ,因而四维速度为
,因而四维速度为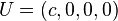 ,这正是在四维时空中的时间方向上运动的含义。
,这正是在四维时空中的时间方向上运动的含义。注意到虽然仅仅在狭义相对论的框架下,四维速度的模总等于光速;但不论是狭义相对论还是广义相对论,它总具有下面的性质:
相对论与黎曼几何-13-四维时空
|||
13. 四维时空
在科学史上,恐怕没有哪一个理论,像相对论这样引发了这么多的“佯谬”。除了双生子佯谬之外,还有滑梯佯谬、贝尔的飞船佯谬、转盘佯谬等等,以及它们的许许多多变种。这些佯谬的产生,根本原因是出于对同时性、时钟变慢、长度收缩、相对性原理、不同参考系的观察者、统一时空等等概念的思考和质疑。时间和空间到底是什么?正如公元四世纪哲学家圣·奥古斯丁对“时间”概念的名言:“Ifno one asks me, I know what it is. If I wish to explain it to him who asks, Ido not know.”我把它翻译成如下两句:“无人问时我知晓,欲求答案却茫然。”相对论是否部分地回答了这个问题?尽管众口难调,见仁见智,但相对论起码为我们提供了一种科学的思路和方法,使我们能从物理数学的理论上较为详细地诠释这些概念,何况还有上百年大量实验结果及天文观测数据的验证和支持呢。修正尚可,否定不易,起码不是诋毁谩骂之辈能做到的。
像双生子佯谬一样,尽管佯谬本身往往涉及到加速度参考系,但分析和理解这些佯谬并不一定需要广义相对论,许多相关的问题也并非一定要使用弯曲时空来解释。况且,正如我们在介绍黎曼几何时提到的,黎曼流形的每一个局部看起来都是一个欧氏空间。那么,对广义相对论研究的弯曲时空而言,它的每一个局部看起来便都是一个闵可夫斯基空间。闵可夫斯基4维时空的性质对广义相对论至关重要,是理解弯曲时空、分析黑洞等奇异现象的基础。因此,我们有必要在介绍爱因斯坦的引力场方程之前,首先多了解一些闵氏时空。
闵可夫斯基时空是欧氏空间的推广,仍然是平坦的。闵氏空间与欧式空间的区别,是在于度规张量的正定性。在黎曼流形上局部欧氏空间中定义的度规张量场gij,是对称正定的。如果将时间维加进去之后,度规张量便不能满足“正定”的条件了。将非正定的度规张量场包括在内的话,黎曼流形的概念被扩展为“伪黎曼流形”。比较幸运的是,之前我们所介绍的列维-奇维塔联络及相关的平行移动、测地线、曲率张量等等概念,都可以相应地推广到伪黎曼流形的情形。
度规张量是一个二阶张量,可以被理解为我们更为熟悉的方形“矩阵”。在矩阵中也有“对称正定”的概念。所谓对称矩阵,是指行和列对换后仍然是原来矩阵的那种矩阵。度规张量的对称性,是由它的定义决定的:
ds2 = gijdxidxj
实际上,任何矩阵都可以分解成一个对称矩阵和一个反对称矩阵之和。根据以上度规的定义可知,gij的反对称部分对ds2的贡献为0,所以,度规张量可以被认为是一个对称矩阵。
矩阵为“正定”的意思可以理解为这个矩阵的所有特征值都是“正”的。欧氏空间度规的正定性意味着实际空间中的距离(弧长)的平方是一个正实数ds2= dx2 + dy2 +dz2。因而,欧氏空间的度规是一个对称正定的d函数,
闵可夫斯基时空的度规仍然是对称的,但却不是正定的:dt2= dt2 - dx2 - dy2 - dz2,其度规记为h函数。上式中的t是时间,x、y、z是3个空间维坐标,而dt取代了弧长ds,被称为固有时。
细心的读者可能会问:时间间隔和空间距离的量纲是不一样的,怎么把它们的平方加减到一块儿去了呢?这儿也是使用了一个约定俗成的原则:将光速定义成了1。也就是说,四维时空的度规本来应该表示成如下形式:c2dt2 = c2dt2 -dx2 - dy2 - dz2,c=1的原则使公式看起来简洁明了,但我们务必随时记住这点。
比较欧氏空间和闵氏空间,将它们的度规d函数和h函数写成矩阵形式:

公式(2-13-2)中,第一维的本征值1对应于时间,其它本征值为-1的3个维度对应于3维空间。
时间和空间统一在4维时空中,是为了数学上的方便。爱因斯坦的狭义相对论揭示了时间空间的相对性及它们之间通过洛伦茨变换的互相关联。然而,时间和空间毕竟是不同的物理概念,时间用时钟来度量,空间用尺子来度量,将它们在4维时空中分别对应于本质不同的实数和虚数,这也反映了“时钟”和“米尺”不能互变的物理事实。
四维时空中的一个点,有时间有地点,按照通常的意义把它叫做一个“事件”。例如,图2-13-1b中的A点,表示粒子初始时刻t1的空间坐标为(x1,y1)这个“事件”,后来,在时刻t2,粒子运动到了空间位置(x2,y2),即粒子最后在时空中的位置,这个“事件”用点B(t2,x2,y2)来表示。图中从A到B的曲线,叫做粒子的“世界线”。
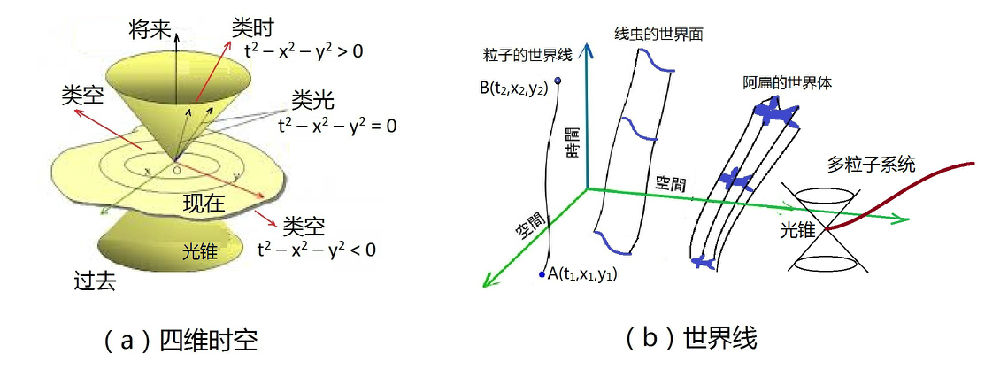
图2-13-1:四维时空和世界线
在上一节中解读双生子佯谬时,将双生子的两次相遇当作2维时空中的两个事件点,然后,便可分别计算两条世界线的“固有时”再加以比较而得到答案。2维闵氏时空中两个任意事件之间直线路径的距离可表示为:
t2 = t2- x2
这个表达式右边的数值为正、零、负,分别定义了两个事件之间的相对关系:是类时、类光、还是类空。如果两事件的关系是类时的,t代表的才是固有时。类时关系说明两个事件之间可以有因果关联。比如双生子中的“刘天出生”(事件O),和“刘天返回地球”(事件D)这两个事件,一定是O在前,D在后,刘天不可能先返回地球再出生,无论从哪个参考系观察,这个结论都不会改变,这是“类时”的特点和物理意义。如果两个事件的关系是“类光”,t2 =0,说明它们互相位于另一个的光锥上,只有速度最快的光才能将它们联系起来。那么,类空(t2 <0)又是什么意思呢?在类空的情形下,两个事件之间的间隔无法叫做“固有时”了,因为它的本质已经不是时间,而更像空间。它可以被另一个物理量,即“固有距离”s来表征:s2= x2- t2。“类空”说明两个事件之间不可能具有因果关系,除非存在超光速的信号,才能将它们互相联系起来,但这是违反狭义相对论的基本假设的。所以,两个类空事件点之间不可能有真实粒子的“世界线”,真实粒子世界线的位置一定在光锥以内,是类时的。类空的两个事件互相位于对方的光锥之外。

图2-13-2:二维闵可夫斯基时空中事件之间的关系
如图2-13-2a中,很容易看出事件之间的关系:相对于事件O而言,事件B、G、F是类时的;事件E是类光的;事件A、C、D是类空的。图2-13-2b中的事件1和事件2互为类空,类空事件的时间顺序可以用坐标变换来改变。比如,从图2-13-2b中可见,事件1和事件2在Bob的坐标系(黑色)和Alice的坐标系(红色)中,发生的时间顺序不一样。在黑色(假设为静止)坐标系中的Bob看来,发生在t=0的事件1先于发生在t=1的事件2。红色坐标系相对于黑色作匀速直线运动,在其中的观测者Alice看起来,事件1仍然发生在t’=0处,但事件2却是发生在t’=-1的地方,发生时间早于事件1发生的时间。因而,这两个类空相关的事件不可能有因果关系。现在,我们再来看看作匀速直线运动的粒子和作匀加速直线运动的粒子的世界线在2维时空中看起来是个什么样子?图2-13-2c画出了它们的曲线形状。
对于作匀速直线运动粒子的情况,我们早就打过交道,因为洛伦茨变换将静止的坐标系变换成相对运动的坐标系。比如说,图2-13-2b中红色坐标系的时间t’轴,实际上就是(t=0,x=0)的粒子,朝着x方向作匀速运动v的世界线。图c中的三条红线,则分别表示t=0时,位于x上不同位置的3个粒子的世界线。也就是说,匀速直线运动粒子的世界线和牛顿力学中将粒子的轨迹表示成时间的函数是一致的,是一条直线。
下面考虑运动粒子作匀加速直线运动的情况,根据牛顿力学中x方向的匀加速运动公式:x=(1/2)at2,应该是一条抛物线,但抛物线很快就跑到了光锥的外面,说明速度增加到超过了光速,这显然不满足狭义相对论光速极限的假设,见图2-13-2c。用相对论可以证明,2维闵氏时空中的匀加速运动粒子的世界线不是抛物线,而是无限靠近光锥的双曲线。“无限靠近光锥”,说明粒子的运动速度越来越大,无限地接近光速,但永远不等于光速。图c中的3条蓝色曲线,便分别对应于3个不同粒子的世界线。但是,读者对此可能又有疑问:不是说的是匀加速运动吗?匀加速运动的加速度应该为常数,如果速度永远不能超过光速的话,这“匀加速”又体现在哪儿呢?这点解释起来有点复杂,不过大家需要明白的是,相对论的关键思想是:观察同一个物理量,不同的参考系将得到不同的数值。这儿的“加速度不变”,是对于作匀加速运动的参考系中的观测者自己而言,是他们自已感觉到的加速度,所谓的“固有加速度”不变。当我们坐在加速运动的汽车上的时候,会感到反方向的惯性力,加速度越大,惯性力也越大,人也越会有不舒服的感觉。那条双曲线表示“匀加速”的意思就是说:沿着这条世界线运动的人将始终保持同样程度的不舒服感。
闵可夫斯基空间中的匀加速运动坐标系叫做伦德勒(Rindler)坐标。伦德勒坐标有许多有趣的性质,是使用平坦的闵氏空间来分析黑洞附近物理的一个强有力的工具,在伦德勒空间中存在类似于黑洞附近的“视界”之类的概念,甚至于还有与“霍金辐射”相类似的“安鲁效应”等量子物理相关的现象。首先弄明白伦德勒空间,对理解真正的黑洞物理有很大帮助,因此,我们将在下一节中介绍它。
- [10]李铭
- 博主回复(2014-11-7 22:26):不是这样的,看我的图中,匀加速世界线上不可能有与45度光锥线左边部分相交的类时线。
==================
这是因为你这个Alice 一开始位于类空区域,加速度大。如果加速度不够大,也可以进入类时区域光锥内部。 - 博主回复(2014-11-7 23:20):什么叫:“你这个Alice 一开始位于类空区域”,类空、类时是两个事件之间的相对关系,没有什么绝对的“类空区域”。无论你将Alice位于哪儿,只要她是作匀加速运动,就对应于一条双曲线的世界线,对双曲线的世界线而言,她和时空中的一部分是不可能通信的。
- [9]李铭
- 博主回复(2014-11-7 21:54):我的意思就是说,空间中任何一点总能作出一条类时线与匀速直线相交。但不是每一点都能作出类时线与匀加速的双曲线相交。
=================
匀加速世界线只要还没有超光速,是可以通过类时线与静止系相交的。 - 博主回复(2014-11-7 22:26):不是这样的,看我的图中,匀加速世界线上不可能有与45度光锥线左边部分相交的类时线。
- [8]李铭
- 第一幅b图(中间那幅)是很误导的,好像Alice 是因为加速而失去联络的。这是不对的。只要她处于光锥之外,即使她静止,她也是失去联络的。类空间隔不可联络,跟加速不加速无关。
- 博主回复(2014-11-7 21:54):我的意思就是说,空间中任何一点总能作出一条类时线与匀速直线相交。但不是每一点都能作出类时线与匀加速的双曲线相交。
- [7]李铭
- 我说的BOB就是你文中的Bob啊。他的世界线有一段在光锥之外,他在那儿是看不到光锥之内的世界的。
- 博主回复(2014-11-7 21:53):明白你的意思了。但我的意思是说,在匀速运动那条世界线上(是一条线,不是一个点),总是有可能可以看到整个空间,也可被整个空间看到。当然是要互为类时的关系。
- [6]徐传胜
- 好文!
- 博主回复(2014-11-7 20:01):谢谢。
- [5]李铭
- 第一幅图中BOB也有一段(光锥之外)是看不到o点出发的完整世界的。
- 博主回复(2014-11-7 19:58):不知道你的BOB指什么,不过我想你说的有你的道理,我会仔细检查下。谢谢。
- [4]李铭
- 第一幅图有点毛病。Alice和Bob应该从同一地点出发,这样开始有一段时间他们三者是相互能看到的。只有当ALICE的速度超过光速飞出光锥以外才失去联络。
- 博主回复(2014-11-7 19:57):第一幅图a的目的主要是想画出这三种运动状态的不同的世界线,不想涉及到他们什么时候在一起,什么时候分开等等。

- [3]qweixin
- 对A、B,为何t=0时,x≠ 0?
- 博主回复(2014-11-7 20:47):打错字:“那一条机械曲线”,应为“那一条双曲线”
- 博主回复(2014-11-7 19:53):在匀加速坐标系中,习惯将原点选在双曲线的两条渐近线的交点。坐标系中所有的双曲线都以这两条光锥线为渐近线,越接近光锥的双曲线,具有更大的固有加速度,实际上,光锥本身也属于这一族双曲线之一,它对应于固有加速度为无穷大的那一条机械曲线。











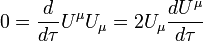


No comments:
Post a Comment