爱因斯坦方程[编辑]
在建立了描述引力效应的相对论性几何化版本后，还有一个关于引力的起源问题没有解决。牛顿理论中的引力来源于质量，而在狭义相对论中质量的概念被包含在更具有一般性的能量-动量张量中。这个张量包含了对系统的能量和动量的密度，以及应力（即压强和剪应力的统称）的描述[25]，通过等效原理就可以将能量-动量张量概括到弯曲的时空几何中去。如果和几何化的牛顿引力作进一步的类比，可以很自然地通过一个场方程将能量-动量张量和里奇张量联系起来，而里奇张量正描述了潮汐效应的一类特殊情形：一团初始状态为静止的测试粒子形成的云的体积会由于这群测试粒子作自由落体运动而变化。在狭义相对论中，能量-动量张量的守恒律在数学上对应着它的散度为零，而这一守恒律也可以被概括到更一般的弯曲时空中，其方法是将经典的偏导数替换为它们在曲面流形上的对应物：协变导数。在这一附加条件下，能量-动量张量的协变散度，以及场方程右边所有可能出现的项统统为零，这一组简洁的方程表述被称作爱因斯坦引力场方程：[26]
构成的并且散度为零的特别组合，这种组合被称作爱因斯坦张量。特别地，
是能量-动量张量。将引力场方程的理论和对行星轨道实际观测的结果（或等价地考虑到弱场低速时近似为牛顿引力理论）相比较，可得到方程中的比例常数
，其中
是万有引力常数而
是光速[27]。当没有物质存在时能量-动量张量为零，这时的爱因斯坦场方程的形式化简为所谓真空解法：
我说广义相对论
![[已注销]](http://img3.douban.com/icon/user_normal.jpg){kind=icon}
来自: [已注销] 2009-09-08 19:31:28
发信人: fft (热血青蛙), 信区: Science
标 题: 《我说广义相对论》之广义协变原理与张量
发信站: BBS 水木清华站 (Thu Jun 28 04:19:29 2001)
《我说广义相对论》之广义协变原理与张量
广义协变原理就是广义相对性原理是广义相对论的两个基本
原理之一，是狭义相对论中的相对论原理的推广，这也正是
广义与狭义名字上区别的由来。
狭义相对性原理：
一切物理定律（引力除外）在惯性参考系中保持相同的形式。
广义相对性原理：
一切物理定律在一切参考系中保持相同的形式。
这里要解释几个名词
参考系：就是以一定方式运动的观察者，他可以定义时空坐标来描述
事件发生的时间和地点，在我们的3+1维时空，这种描述需要
4个实数。当然这种坐标的定义方式是任意的，每种定义方式
可以叫做一个坐标系。
惯性系：一个参考系，如果其中的物体满足在合力为零的情况下保持匀
速运动或静止状态，那么这个参考系就叫做惯性参考系。
物理定律：就是一些物理量和另一些物理量之间的相等关系。
为了满足相对性原理，就要对物理定律的形式做出修改，否则连普通的
力学都不满足这个原理。最简单的例子就是在非惯性系中的牛顿力学，
还记得相对加速度，牵连加速度，科氏加速度这些名词吧，当年我可是
被绕了够呛。跟惯性系的牛顿定律比，它们显然不是一个形式。为什么
会这样呢？因为坐标变换后，物理量一般不会保持原来的值，而是要变
化，变化的方式当然跟坐标变换的方式有关了，所以原来相等的关系可
能就会不等了。
按照这样的思路，如果把物理定律表示成这样的等式，它的两边在
坐标变换下按照相同的规律变化，那么原来相等的东西变换后也一定相
等，这样就可以得到符合广义相对性原理的物理定律的形式。下面的任
务就是研究物理量在坐标变换下如何变化了，只要把按照相同规律变化
的物理量放到一起组成物理定律，问题就解决了。
物理量随坐标系的变换很复杂，有的量不随坐标系变化，比如质点
的质量，这种量很容易对付，他们在坐标变换下不变，可以认为已经满
足了广义协变原理，所以不必考虑。有的不仅与自身在原坐标系中的值
有关，还和其他的量有关，这样就必须把这些相互关联的一组量同时加
以考虑。我们的经验发现，同时变化的量的个数、都是空间维数的某个
自然数幂，考虑到前面说的不随坐标变换变化的量，它的个数是1，所以
幂次是0，所以同时变化的量的个数、都是空间维数的某个非负整数幂。
根据这个幂次的不同，可以对物理量进行分类。首先，把这种按一定规
律随坐标系变化而变化的物理量组称为张量，如果张量中物理量的个数
是空间维数的n次幂，就把这个张量叫做n阶张量。
阶数相同的张量具有相同的个数（废话！）和变换规律，所以最后
的方程应当由阶数相同的张量来组成。我们把物理定律在一个参考系下
用张量方程写出来，就可以知道它在一切其他参考系下也是这样的形式，
只不过，要用经过变换的张量来代替原来的。现在唯一的问题是，张量
在坐标表换下如何变化？
下面不得不写点数学公式了。设原坐标系Xi，i是坐标编号，应该是
从0到3，新坐标系是X'i(Xi),写成函数形式表示他们的变换关系。0阶张
量就不说了，它们不变。对于一阶张量Ai，变换关系有两种：
A'i=Aj*dX'i/dXj A'i=Aj*dXi/dX'j
先解释一下，这两个式子应用了爱因斯坦求和约定，即相同的下标表示
对此下标从0到3求和，这个式子里的j就是这样的下标。在此约定下，张
量方程可以写成很简单的形式。回到主题上来，这两种1阶张量是不同的
前一种叫做1阶逆变张量，后一种叫做1阶协变张量。对于更高阶的张量，
因为有4^n个，所以要引入n个从0到3的下标将它们适当的编号,使得他们
满足变换关系类似的，不过要注意，此时有的下标满足逆变的变换关系，
有的满足协变的，这种就叫做混合张量，一般写成(p,q)型张量，表示有
p个逆变下标，q个协变下标。举例来说，(1,1)型张量的变换关系是：
A'{i1,i2}=A{j1,j2}*dX'i1/dXj1*dXi2/dX'j2
其他型号的张量也可类似的写出变换关系，说白了就是原张量的某个线
性和。为了书写上的方便，逆变指标写在右上角，协变指标写在右下角
，不过bbs上无法用角标，我就用下面的方式代替了，花括号表示指标集
，;前面的是逆变指标，后面的是协变指标：A{i1;i2},B{i,j;k,l,m}等
等。
还有几个问题：
为什么是线性和？是因为从对称性的角度变换和逆变换的形式应当
一样，所以只能是线性变换。
为什么是齐次的？是因为非齐次项没有作用，方程两边都有，所以
就减掉了。
变换系数为什么只有这两种？还是从逆变换的角度考虑变换方程的
形式应当不变，这样自然可以推出系数。
张量的分类与变化规律就这样结束了。有了这些，就可以写出满足
广义写变性要求的物理定律了。
总之一句话，广义相对性原理要求物理定律用张量方程。这就是广
义相对性原理的唯一作用。
标 题: 《我说广义相对论》之广义协变原理与张量
发信站: BBS 水木清华站 (Thu Jun 28 04:19:29 2001)
《我说广义相对论》之广义协变原理与张量
广义协变原理就是广义相对性原理是广义相对论的两个基本
原理之一，是狭义相对论中的相对论原理的推广，这也正是
广义与狭义名字上区别的由来。
狭义相对性原理：
一切物理定律（引力除外）在惯性参考系中保持相同的形式。
广义相对性原理：
一切物理定律在一切参考系中保持相同的形式。
这里要解释几个名词
参考系：就是以一定方式运动的观察者，他可以定义时空坐标来描述
事件发生的时间和地点，在我们的3+1维时空，这种描述需要
4个实数。当然这种坐标的定义方式是任意的，每种定义方式
可以叫做一个坐标系。
惯性系：一个参考系，如果其中的物体满足在合力为零的情况下保持匀
速运动或静止状态，那么这个参考系就叫做惯性参考系。
物理定律：就是一些物理量和另一些物理量之间的相等关系。
为了满足相对性原理，就要对物理定律的形式做出修改，否则连普通的
力学都不满足这个原理。最简单的例子就是在非惯性系中的牛顿力学，
还记得相对加速度，牵连加速度，科氏加速度这些名词吧，当年我可是
被绕了够呛。跟惯性系的牛顿定律比，它们显然不是一个形式。为什么
会这样呢？因为坐标变换后，物理量一般不会保持原来的值，而是要变
化，变化的方式当然跟坐标变换的方式有关了，所以原来相等的关系可
能就会不等了。
按照这样的思路，如果把物理定律表示成这样的等式，它的两边在
坐标变换下按照相同的规律变化，那么原来相等的东西变换后也一定相
等，这样就可以得到符合广义相对性原理的物理定律的形式。下面的任
务就是研究物理量在坐标变换下如何变化了，只要把按照相同规律变化
的物理量放到一起组成物理定律，问题就解决了。
物理量随坐标系的变换很复杂，有的量不随坐标系变化，比如质点
的质量，这种量很容易对付，他们在坐标变换下不变，可以认为已经满
足了广义协变原理，所以不必考虑。有的不仅与自身在原坐标系中的值
有关，还和其他的量有关，这样就必须把这些相互关联的一组量同时加
以考虑。我们的经验发现，同时变化的量的个数、都是空间维数的某个
自然数幂，考虑到前面说的不随坐标变换变化的量，它的个数是1，所以
幂次是0，所以同时变化的量的个数、都是空间维数的某个非负整数幂。
根据这个幂次的不同，可以对物理量进行分类。首先，把这种按一定规
律随坐标系变化而变化的物理量组称为张量，如果张量中物理量的个数
是空间维数的n次幂，就把这个张量叫做n阶张量。
阶数相同的张量具有相同的个数（废话！）和变换规律，所以最后
的方程应当由阶数相同的张量来组成。我们把物理定律在一个参考系下
用张量方程写出来，就可以知道它在一切其他参考系下也是这样的形式，
只不过，要用经过变换的张量来代替原来的。现在唯一的问题是，张量
在坐标表换下如何变化？
下面不得不写点数学公式了。设原坐标系Xi，i是坐标编号，应该是
从0到3，新坐标系是X'i(Xi),写成函数形式表示他们的变换关系。0阶张
量就不说了，它们不变。对于一阶张量Ai，变换关系有两种：
A'i=Aj*dX'i/dXj A'i=Aj*dXi/dX'j
先解释一下，这两个式子应用了爱因斯坦求和约定，即相同的下标表示
对此下标从0到3求和，这个式子里的j就是这样的下标。在此约定下，张
量方程可以写成很简单的形式。回到主题上来，这两种1阶张量是不同的
前一种叫做1阶逆变张量，后一种叫做1阶协变张量。对于更高阶的张量，
因为有4^n个，所以要引入n个从0到3的下标将它们适当的编号,使得他们
满足变换关系类似的，不过要注意，此时有的下标满足逆变的变换关系，
有的满足协变的，这种就叫做混合张量，一般写成(p,q)型张量，表示有
p个逆变下标，q个协变下标。举例来说，(1,1)型张量的变换关系是：
A'{i1,i2}=A{j1,j2}*dX'i1/dXj1*dXi2/dX'j2
其他型号的张量也可类似的写出变换关系，说白了就是原张量的某个线
性和。为了书写上的方便，逆变指标写在右上角，协变指标写在右下角
，不过bbs上无法用角标，我就用下面的方式代替了，花括号表示指标集
，;前面的是逆变指标，后面的是协变指标：A{i1;i2},B{i,j;k,l,m}等
等。
还有几个问题：
为什么是线性和？是因为从对称性的角度变换和逆变换的形式应当
一样，所以只能是线性变换。
为什么是齐次的？是因为非齐次项没有作用，方程两边都有，所以
就减掉了。
变换系数为什么只有这两种？还是从逆变换的角度考虑变换方程的
形式应当不变，这样自然可以推出系数。
张量的分类与变化规律就这样结束了。有了这些，就可以写出满足
广义写变性要求的物理定律了。
总之一句话，广义相对性原理要求物理定律用张量方程。这就是广
义相对性原理的唯一作用。
广义相对论的学习总结
2013-09-26 16:36:54 来自: 忘川 (失去的乐园，才是真正的乐园)
广义相对论引论(第二版)的评论
5
广义相对论的学习总结
1.引言
1.1前言
经过过去一年对广义相对论的学习，基本对广义相对论的基本原理和运用有了比较完整的认识。这篇文章是为了总结自己学习的体会，尽量用自己的语言谈谈对广义相对论的理解。由于作者水平有限，也为了文章的简洁，所以省去数学推导，仅保留基本的数学公式和方法说明。
广义相对论是爱因斯坦一大理论成果，可以解释宏观世界一切物体的运动，可以在一切坐标系下运用，本身又保持了相当完美的对称性和简洁性。随着空间探测技术的发展，广义相对论的许多结论都得到了证明，而广义相对论和量子力学构成了现代物理的两大支柱。
1.2导语
在具体介绍广义相对论的内容之前，我想用自己的语言，对广义相对论的思想和研究问题步骤做一个小的总结和介绍。总的来说，广义相对论是建立在四个假设之上，通过这四个假设，爱因斯坦认为惯性场和引力场等效，以及所有参考系的平权性。然后爱因斯坦把引力场认为是一种几何效应。是由于质量在空间上的分布不均匀，导致空间的空间扭曲。
在数学上，用张量来代表物理量，以满足物理规律在所有参考系下都成立。用黎曼几何来刻画弯曲空间，联络来描述引力强度，曲率张量来描述空间弯曲，度规张量来描述引力势。
接下来便是构建场运动方程。我们可以用惠曼的名言总结道：“物质告诉时空如何弯曲，时空告诉物质如何运动。”按照爱因斯坦的想法，引力是由于质量空间分布不均匀造成的几何效应。所以爱因斯坦场方程左边应该是反映时空的几何性质的张量，右边是能动张量。再继续利用能量守恒定律，便可以推出爱因斯坦场方程。
应用爱因斯坦的场方程，得到了很多新奇的结论和实验预言，并且以“水星进动”和“引力红移”为代表的实验验证了广义相对论的正确性。
广义相对论还预言了引力弯曲效应极大情况下黑洞的存在。
而广义相对论作为宇宙学的理论基础，特别是近几十年观测技术的进步，使得宇宙学建立起了相对完整的理论系统。
2.基本假设
广义相对论建立在以下假设下。
2.1等效原理
广义相对论用的是强等效原理。
引力场与惯性场的的一切物理效应都是局域不可分辨的。
2.2马赫原理
惯性力起源于物质间的相互作用，起源于受力物体相对于遥远星系的加速运动，而且与引力有着相同或相近的物理根源。
2.3广义相对性原理
一切参考系都是平权的，物理定律在任何坐标系下形式都不变，即具有广义协变性。
2.4.光速不变原理
任意观测者测量的光速都是c。
a和b假设了惯性场和引力场以及惯性力和引力的局域等同性，在后来引入黎曼几何后，惯性力场可以运用空间的几何性质联络来描述，由于惯性力场和引力场的局域等同性，所以引力场也可以运用联络来描述，于是完成了引力的几何化，把引力看做空间的弯曲造成的几何效应。从而解决了狭义相对论无法描述引力的困难。C假设否决了过去一直寻找的惯性系的存在，解决了狭义相对论中寻找惯性系的困难。D假设是从狭义相对论开始就有的，也是最有实验依据的。从光速不变原理出发，可以得到狭义相对论的很多结果。不过在广义相对论中，把规则者从惯性系扩大到任意参考系，和c一起假设了参考系的平权性。
3.数学基础
广义相对性原理和光速不变原理说明了一切参考系都是平等的，这就要求了物理规律要在一切参考系下成立，从而要涉及到物理量在坐标系之间的变换关系，特别是任意弯曲坐标系下的变换。从而需要张量分析来描述这种变换。而马赫原理和等效原理又把引力解释为空间的几何弯曲效应，于是也需要一种新的几何学来描述物体在弯曲空间的运动。从而传统的运用在平直空间的欧式几何已经不再适用，所以我们要继续介绍黎曼几何。
3.1张量分析
借助张量分析，广义相对论把物理规律表达为张量方程。
3.1.1定义：
一个数组，在坐标变换下，如果每一个指标都按坐标微分的变换规律进行变换，则为逆变张量。如果都按坐标微分的逆变换，则为协变张量。
因为在定义张量的同时，给出了在坐标变换时张量的变换规律，所以在任意坐标下，该张量都被唯一的确定下来了，所以张量是在坐标变换时不变的量。
运用张量的定义，因为张量是在坐标变换下不变的量，所以可以把物理量用张量表示。
3.1.2平移：
张量是逐点定义的，所以两个不同点上的张量相减后将失去张量的性质。而广义相对论要把物理规律用微分方程的形式来表达，微分计算需要运动不同点的相减。所以引入了张量的平移，在相减前，先将张量移到同一个点上。
不同点的坐标系不一样，所以同样的张量，平移移动会产生坐标差。
坐标改变量与张量本身以及距离的比例，称为联络。
联络的求法为：
联络代表了两点之间坐标系的改变的剧烈程度，而每点的坐标系又是沿着空间表面建立的，所以联络可以代表空间的弯曲程度，可是联络与空间坐标系有关，不同的坐标系下联络不同，不能代表空间的属性。所以我们定义一个专门的由联络组成的量来描述空间的弯曲程度。
称为曲率张量，可以用来描述空间的弯曲程度。
3.1.3运动：
在欧式空间中，直线被定义为线上任意相邻两点的切矢量都相互平行的曲线，我们把它推广到任何空间中，并把推广后的直线成为测地线。
由于对于推广的任何空间，我们尚未清楚它的度量关系。所以先不考虑空间距离之类的度量关系，我们把这种没有度量的任意弯曲程度的空间称为仿射空间。
运用测地线上任意相邻两点的切矢量都相互平行的我们可以很快求出测地线的微分方程。即把A点的切矢量移动到B点后，和B点的切矢量成比例关系。
把比例系数按dλ的进行展开，保留到一级小量：
联立平移公式和切矢量的微分公式，并保留到一级小量，便可得出：
便为测地线的微分方程。
在欧式空间中，物体沿直线运动，在推广的仿射空间中，物体沿测地线运动，沿测地线运动距离最短。这便是著名的爱因斯坦最短程原理。
3.1.4度量和运算：
为了在空间中引入长度等物理量，我们引进度规张量，来确定两点之间的距离。
在经典的欧式空间中：
狭义相对论运用的闵柯夫斯基空间：
有了以上的基础，便能建立起一个新的空间——黎曼空间。黎曼空间有其特殊的联络和度规张量，广义相对论便建立在黎曼空间的框架下。在广义相对论中，将会把引力几何化，联络便可以看做是引力强度，而度规张量则会是引力势。研究曲率张量，度规张量和能动张量的关系，便能导出爱因斯坦场方程。我们将在后面介绍黎曼几何。
3.2黎曼几何
3.2.1黎曼空间和度规张量
在仿射空间中引入度规场和不变距离，就构成了黎曼空间。
对一个黎曼空间，如能适当选取坐标，使它的度规张量具有形式
则叫它平坦的黎曼空间。
在线性代数中有这样一条定理：
对常系数二次型 ，若det︱ ︱不为零，则必能找到一个坐标变换，把这个二次型化为坐标微分的平方和或平方差。在黎曼空间中度规一般不是常数，这时上述定理告诉我们，总可以用坐标变换把任一P点的度规化成上式的形式，此外还可以有推论：如果区域V内的度规张量是常数，那么V内的空间是平坦的。
3.2.2联络
仿射空间中借助联络定义了矢量的平移，黎曼空间中进一步要求平移操作保持矢量的长度不变，可以证明，如采用对称联络，那满足这附加要求的联络完全由度规场决定，这种联络叫做Christoffel联络。
我们可以通过计算得到
上面的公式说明了，若在黎曼空间内确定了度规，并采用对称联络，那么这联络完全由度规和它的普通微商决定。
可以证明如下定理：在坐标 下P点的联络为 。我们总可以找到坐标变换 ，使得
那么这条定理有何含义呢？若在坐标 下P点的联络为0，易得
即在P点附近的 的二级小量可忽略的小区域内 近似为常数，我们已经知道， 为常数的区域是平坦的。这样导致了一个结论：对采用对称联络的黎曼空间中的任一点P，总可以找到一组适当的坐标，使得从这组坐标看来P点的领域是近似平坦的。这个结论正是广义相对论中等效原理的数学基础。
3.2.3黎曼空间中的测地线
我们知道，当采用仿射参量时，测地线方程将有简单的形式，我们可以利用黎曼空间中的度规张量来引入这个仿射参量。
对任意一条曲线可以引入一个标量积分
其中ds是曲线上相邻两点的不变距离，P0是曲线上的固定点，P是曲线上的任意点，则s叫做P0到P的固有长度。它是标志曲线上的点的一个自然地标量性参量。
以s为参量，切矢量 定义为
易知，这切矢量总是单位矢量，即
对上式求协变微商，注意到 ，则有
式中左边两项相等，于是得到
若把测地线方程写成
解出f（s）
注意到
则有
这就证明了s是仿射参量，相应的测地线方程是
4.爱因斯坦场方程
在以上数学基础上，我们可以逐步推出新的运动方程。该运动方程将满足基本假设，即引力场和惯性场的等效性，从而可以用空间的几何性质来描述引力场。根据马赫原理，惯性力被认为是起源于加速物体与遥远星系的相互作用，即惯性力与物质的运动有关，从而引力也与物质运动有关。而狭义相对论中，质量和能量等效，所以运动可以看做是物质质量分布的变化。所以引力的效果，是来源于物质质量分布的几何效应。
4.1爱因斯坦场方程的建立
等效原理推广了引力的概念，并暗示了有引力场的时空是弯曲的黎曼空间，引力场的物理效果可以通过黎曼空间的度规张量来体现。为了完成新的引力理论，需要找到度规场分布的物理规律，即度规场（或叫推广的引力势）所满足的微分方程，但是这方面没有直接可依据的观测知识，所以能采取的途径是作猜测性的推理。
参照牛顿引力理论，我们可以得到这些设想，首先，牛顿引力势的分布取决于静态物质的密度分布，所以度规场应取决于物质的动量能量张量，因为在张量性的物理理论中物质密度是动量能量张量的一个分量。这样我们把度规场方程的数学形式确立为
其中 是物质的动量能量张量， 是由度规 及其微商构成的张量。其次，牛顿引力方程
是一个引力势的二阶线性偏微分方程，因此要求 最高只含有 的二阶微商，且对二阶微商是连续的。
据上述推测和数学知识， 最一般只能是
为里奇张量，是曲率张量的缩并：
其中角标是任意常参量，注意到能量动量的守恒，它表现为 的四维协变散度等于零，即
因此 应满足
我们把 和R组合成爱因斯坦张量 ，这样度规场方程就取得了具体形式
其中 叫做相对论引力常数， 是唯一剩下的任意参量，最简单的可能是令 =0，相应的方程
叫爱因斯坦引力场方程。
4.2宇宙项
场方程加入任何一个散度为零的项，不会影响 的成立，所以爱因斯坦场方程又可以写成：
其中λ称为宇宙项。
虽然宇宙项对爱因斯坦场方程的建立没有影响，然而宇宙项大体会引起“斥力”效应。在爱因斯坦早期尝试建立静态宇宙模型时，曾经加入加入了宇宙项，当观测事实证明宇宙在膨胀时，爱因斯坦又放弃了宇宙项，并称之为他一生最大的错误。
不过近年来关于暗能量的探讨，猜测暗能量是宇宙项引起的效应。
4.3牛顿近似
由于牛顿引力方程在观测和应用领域都取得了极大成功，所以爱因斯坦场方程不能否定牛顿引力方程。应该把牛顿引力方程看做是爱因斯坦场方程在特殊情况下的近似。
所以当满足以下条件下，爱因斯坦场方程可以化成牛顿引力方程。
引力场为弱场，所以令：
为闵柯夫斯基联络。
引力场是静态的：
引力场是空间缓变的：
粒子的运动是低速的：
为了简化问题，我们考虑一片非相对论性理想流体组成的介质，它在某参考系中为静止介质。由狭义相对论知，它的动量能量张量为：
为物体的四维速度。
为固有时，表示四维空间中，两个事件的距离。
所以
采用相对介质静止的坐标系，
所以只有一个不为零的分量：
再计算里奇张量
利用克里斯托夫联络，保留至一级小量，联络可以表示为：
它的分量可以写为：
因为联络为一级小量，所以忽略里奇张量关于联络的二次项：
如此得到，里奇张量的简化形式：
写为逆变形式为：
以上一切都准备好之后，我们可以写出00分量的场方程：
代入具体的有关量，得到：
所以我们要求 。
利用测地线方程在牛顿近似条件下，将会化为牛顿第二定律：
利用条件四：
所以测地线方程可以写成：
利用牛顿第二定律：
所以
又因为无穷远处，引力场为零，即 时， ，所以：
代回
得到：
与牛顿引力方程形式完全一样。
所以：
至此我们已经证明牛顿引力方程为爱因斯坦场方程特殊情况下的近似，牛顿第二定律为测地线方程的近似，并且我们得到了 的数值。
5.广义相对论的若干推论和实验验证
5.1引力红移
当从远离引力场的地方观测时，处在引力场中的辐射源发射出来的谱线，其波长会变长一些，也就是红移。
理论证明详见6.2.3
二十世纪六十年代，庞德、雷布卡和斯奈德采用穆斯堡尔效应的实验方法，测量由地面上高度相差22.6米的两点之间引力势的微小差别所造成的谱线频率的移动，定量地验证了引力红移。结果表明实验值与理论值完全符合。
5.2引力时间延迟效应
时间延迟效应是指当雷达信号途径一个大质量天体时，在观测者看来这个信号发射到指定目标以及返回的时间都要比没有大质量天体存在时所需的时间略长。
理论证明：
从狭义相对论可知，时钟在高速运动时会变慢，广义相对论中，引力场和惯性场等效，所以引力场中的时钟也可以看做在做加速运动，所以也会变慢，具体数学推导参见《广义相对论基础》。
第一次实验观测是借助麻省理工学院的“草堆”雷达天线（Haystack radar antenna）完成的，其结果和理论预测符合得很好，误差小于5%。其后这种实验被不断重复，并且不断取得更高的精度。1976年的海盗号火星探测器将精度提高到了0.1%；而2003年的卡西尼号土星探测器的实验则达到了小于0.002%，是迄今为止精度最高的广义相对论实验验证。
5.3水星近日点的进动
详见6.2.2
5.4光线在太阳引力场中的偏折
详见6.2.4
6.广义相对论的应用
6.1动力学：球对称引力场
在建立起广义相对论的基本框架后，接下来便要运用广义相对论来做出理论预言，以及用实验来证明理论。
而最为简单的情况，则是球对称的引力场。
首先在球对称的引力场中引入度规张量，在这个过程中，由于球对称保证了绕对称轴做无穷小转动都保持了度规场不变，所以可以引入凯林矢量场，运用凯林方程组，再进行化简，得到一般球对称的引力场的度规张量形式如下：
6.1.1席瓦西尔外部解
为了进一步简化问题，我们令空间的曲率为零，引力源静止，求得了静止球对称引力源外部的引力场。
运用克里斯多夫联络：
曲率张量的定义：
毕安基恒等式：
并利用牛顿近似：
联立上述式子，并化简得到结果
这便是球对称外引力场的席瓦西尔解。而牛顿万有引力公式描述的也是静止球对称引力源外部的引力场，所以席瓦西尔解正是牛顿万有引力定律的相对论对应。
从结论我们可以看出，该引力场和牛顿引力场有很重要的共同点，球外引力场只取决于引力源的总质量，而与引力源的大小和物质分布无关。通过观测这种引力场，我们只能得到引力源的总质量，而不能得到其它信息。
之后再运用伯克霍夫定理，可以证明席瓦西尔解也可以运用在运用的球对称源的外引力场。
6.1.2席瓦西尔内部解
我们得到了球对称源外部引力场，接下来我们看下内部引力场的分布问题。
设引力源为静止的理想流体，则其能量动量张量有如下形式：
其中，对于静止流体来说：
所以混合形式的能动张量为
而混合形式的爱因斯坦方程为：
又因为能量守恒：
则：
再利用衔接条件，恒星表面r=R处的边条件是 , 与 与席瓦西尔外部解相衔接，即：
联立上述几式，并进行化简得：
当恒星由均匀介质组成时，即：
积分可得：
该解便是静止引力源中的内部引力场，又称为席瓦西尔内部解。
6.2运动学
6.2.1席瓦西尔场中的运动方程
有了动力学之后，我们便可以进一步讨论运动学问题。
由上面给出的黎曼几何几何可知，物体在黎曼空间的运动满足测地线方程。将席瓦西尔场的测地线方程进行初积分，可以得到以下四个方程：
经整理可得：
这便是席瓦西尔场中的运动方程。通过这组方程，我们可以得到一些很有趣的结论。通过方程我们可以得到质点的能量方程：
其中 = 。在前面的介绍中，我们说联络相当于引力场强，而度规张量相当于引力势，所以我们相当于得到了质点的能量与该点的引力势成反比。这就是所谓的质点能量的引力红移。
6.2.2行星的轨道问题：水星的进动角
在牛顿引力理论中，一直有一个难题难以解决，那就是水星的进动角问题，理论预测的水星进动角比实测的要大很多。而广义相对论很精确的求解了水星的进动角。
把席瓦西尔场的运动方程进行化简可得到：
利用数学物理方法的知识，利用线性叠加，可以求得方程的通解：
利用此方程，求得水星的进动角：
与观测相符，也成为了证明广义相对论的重要实验依据。
6.2.3光的引力偏折
按照狭义相对论的质能等效方程： E=mc^2，和普朗克公式E=hν，可以得到光子应具有引力质量，那么光子也必然会受到其他物体的引力场的作用。利用席瓦西尔场的运动方程，再利用光速不变原理：
得到光子的轨道方程
令
方程可以化为：
利用逐级逼近，求得偏折光线的一级近似角
利用该式，可以求得光线的偏折角：
对于太阳来说，
在1919年5月放生日全食的时候，两个 观测队第一次实测了经过太阳表面的星光的偏折所得的结果和相对论结果相符。
6.2.4光的引力红移
光子的频率同样会受引力场的影响，光子的能量为
所以：
又因为
所以
代入席瓦西尔场的度规：
结果说明离引力中心越远的地方测到的频率越小，因此称为引力红移。
6.3黑洞
黑洞是广义相对论预测的，引力场强度极强时的一种特殊的天体。以下只做简单的介绍，不做推理和证明。
6.3.1黑洞的生成：
人们一般认为今天尚能存在的黑洞有三种现实的形成机制：
早期宇宙高密介质中由于密度涨落而造成的小黑洞，质量大约只有 千克。
正常恒星演化到晚期的一种可能的终局，这种黑洞应该是几个至几十个太阳质量的大小。
超重星、星团或星系核塌缩形成的巨型黑洞，它的质量是10^4~10^5太阳质量的量级。
6.3.2黑洞动力学：
黑洞的动力学规律是博肯斯坦和霍金等人在1972至1973年间得出来的，其中最重要的是关于黑洞过程不可逆性的黑洞动力学第二定律：
黑洞动力学过程中视界的总面积不能减少。
即：
也叫面积不减定律。
按面积不减定律，黑洞过程保持视界总面积不变是可能的，这种动力学过程被称作可逆的黑洞过程，视界面积增加的过程则是不可逆的黑洞过程，这一切在形式上与热力学第二定律非常相似。
6.3.3黑洞辐射：
博肯斯坦进一步证明了黑洞的视界面积A正是热力学意义下的熵，黑洞的熵S与视界面积A的关系为：
黑洞表面附近的真空涨落产生虚粒子对，当其中负能虚粒子通过隧道效应而进入黑洞，黑洞的能量将减少，同时其中的正能粒子可能向外穿出黑洞的引力区，这相当于黑洞辐射了一个粒子，这种机制称为霍金辐射。
本评论版权属于作者忘川，并受法律保护。除非评论正文中另有声明，没有作者本人的书面许可任何人不得转载或使用整体或任何部分的内容。
作者: 俞允强
isbn: 7301033176
书名: 广义相对论引论(第二版)
页数: 178
定价: 11.50
出版社: 北京大学出版社
装帧: 精装(无盘)
出版年: 2004-1忘川的其他评论 · · · · · ·
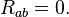
> 我来回应