看麦克斯韦方程，刚开始就遇到了问题，那个倒三角的微分算子对电场的叉乘、磁场的叉乘
http://bbs.rfeda.cn/read-htm-tid-16892.html
简单来说，前面两个叉乘表示 ：电场的空间变化会引起磁场的时间变化，磁场的空间变化会引起电场的时间变化。同时看出传播方向与电磁场方向垂直，所以电磁波是个横波。 l U$0e0 9
后面两个点乘 表示H和D在边界不能突变，是连续的。
逆流而上
高斯磁定律：
是渦胞的質量密度，對應於磁導率，
、
、
分別為渦胞的週邊速度向量的三個投影於x-軸、y-軸和z-軸的分量，對應於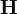
的三個分量。
色散或吸收：
和是頻率的函數。因果論不允許物質具有非色散性，例如，克拉莫-克若尼關係式。場與場之間的相位可能不同相，這導致和為複值，也導致電磁波被物質吸收[20]。
：彎曲時空中的麦克斯韦方程组
物質和能量會造成時空彎曲。這是廣義相對論的主題。時空彎曲會影響電動力學的物理。一個電磁場所擁有的能量和動量也會造成時空彎曲。將平直時空的方程組中的偏導數，替換為協變導數，就可以得到彎曲時空中的馬克士威方程組。採用高斯單位制，馬克士威方程組表達為
是表徵時空彎曲的克里斯托費爾符號。
1
是万有引力常数，
（标量曲率）是里奇张量的迹。应力-能量张量来源于粒子的应力和能量，但同时也来源于电磁场，这造就了非线性。
若你的场是一个流速场,则该场的散度是该流体在某一点单位时间流出单 O(D2F $VlL
位体积的净流量. 如果在某点,某场的散度不为零,表示该场在该点有源, Sw5-^2x 0'
例如若电场在某点散度不为零,表示该点有电荷,若流速场不为零,表是在 T5.^ w
该点有流体源源不绝地产生或消失(若散度为负). 这一点也不难理解,你 3hUP > F8
把Gauss's law写下来就明白这是什么意思了. |' ) P Q
rK:cUW0]X
旋度告诉你的是,一个场在某处,沿着一无穷小的平面边界做环积分,平 2' ^ 7G@%
面法向量即由旋度向量给定,旋度向量的长度则是单位面积的环积分值. K' <[kh:cl
基本上旋度要衡量的是一向量场在某点是否有转弯. 这件事只要你把 CXyb 8z4/+
Stoke's law写下来就一清二处了....
2楼
gwzhao
找了一个描述比较系统的给你看看。 @!" ) shc
麦克斯韦方程组 |/K| Vw a
关于静电场和稳恒磁场的基本规律，可总结归纳成以下四条基本定理： )(G<(e iD
静电场的高斯定理： #k9 &OS?
静电场的环路定理： PFp!T [)
稳恒磁场的高斯定理： TQO |C?
磁场的安培环路定理： W Pd : t
上述这些定理都?****铝⒌馗?隽司驳绯『臀群愦懦〉墓媛桑?员浠?绯『捅浠?懦〔⒉皇视谩?span style="display:none"> yn A_Z ^j
I ? D=Q $s
麦克斯韦在稳恒场理论的基础上，提出了涡旋电场和位移电流的概念： 3 Y#
1. 麦克斯韦提出的涡旋电场的概念，揭示出变化的磁场可以在空间激发电场，并通过法拉第电磁感应定律得出了二者的关系，公式表明，任何随时间而变化的磁场，都是和涡旋电场联系在一起的。 kKF=%J ?X
2. 麦克斯韦提出的位移电流的概念，揭示出变化的电场可以在空间激发磁场，并通过全电流概念的引入，得到了一般形式下的安培环路定理在真空或介质中的表示形式，公式表明，任何随时间而变化的电场，都是和磁场联系在一起的。 - I{op wd
综合上述两点可知，变化的电场和变化的磁场彼此不?****铝⒌模??怯涝睹芮械亓?翟谝黄穑?嗷ゼしⅲ?槌梢桓鐾骋坏牡绱懦〉恼?濉Ｕ饩褪锹罂怂刮さ绱懦±砺鄣幕?靖拍睢?span style="display:none"> C L2zZk{u_
R }I4'
在麦克斯韦电磁场理论中，自由电荷可激发电场 ，变化磁场也可激发电场 ，则在一般情况下，空间任一点的电场强度应该表示为 H 2 I
又由于，稳恒电流可激发磁场 ，变化电场也可激发磁场 。 4}D&=0 I Z
因此，在一般情况下，电磁场的基本规律中，应该既包含稳恒电、磁场的规律，也包含变化电磁场的规律， C4E }.``Hm
M#2<|VUW,
根据麦克斯韦提出的涡旋电场和位移电流的概念，变化的磁场可以在空间激发变化的涡旋电场，而变化的电场也可以在空间激发变化的涡旋磁场。因此，电磁场可以在没有自由电荷和传导电流的空间单独存在。变化电磁场的规律是： ;gEEdx'&T
1.电场的高斯定理 在没有自由电荷的空间，由变化磁场激发的涡旋电场的电场线是一系列的闭合曲线。通过场中任何封闭曲面的电位移通量等于零。 ]z7 pa^
2.电场的环路定理。 n Zj&Ma 7R
3.磁场的高斯定理 变化的电场产生的磁场和传导电流产生的磁场相同，都是涡旋状的场，磁感线是闭合线。因此，磁场的高斯定理仍适用。 ?_{ {ii l
4.磁场的安培环路定。 8 5"Sz c-#
umPN=0u6
-;Mh |!y g
在变化电磁场的上述规律中，电场和磁场成为不可分割的一个整体。 O:V. ;q2]U
_JpTHpqu
将两种电、磁场的规律合并在一起，就得到电磁场的基本规律，称之为麦克斯韦方程组。 # ( 4 )ps.
'u PI~l`g
上面四个方程可逐一说明如下：在电磁场中任一点处 1(aib ^!B
（1）电位移的散度 等于该点处自由电荷的体密度 ； sAX4giaL D
（2）电场强度的旋度 等于该点处磁感强度变化率 的负值； B_c-@kl
（3）磁场强度的旋度 等于该点处传导电流密度 与位移电流密度 的矢量和； 4 ti Cx f)
（4）磁感强度的散度 处处等于零。 >4lA +1JYk
麦克斯韦方程是宏观电磁场理论的基本方程，在具体应用这些方程时，还要考虑到介质特性对电磁场的影响， )1 0 aDTlr
以及欧姆定律的微分形式 。 pkIJbI{aS
]x_ 1 4$rk
方程组的微分形式，通常称为麦克斯韦方程。 g e pY V}
G n qun %
在麦克斯韦方程组中，电场和磁场已经成为一个不可分割的整体。该方程组系统而完整地概括了电磁场的基本规律，并预言了电磁波的存在。
逆流而上
3楼
cxw770
级别: 积极交流四级
显示用户信息 UID: 14900
精华: 0
发帖: 367
rf币: 753 个
威望: 0 点
技术分: 4 点
版主等级: 0 级
研究方向: HFSS
注册时间: 2008-07-07
最后登录: 2009-10-19 cxw770 发表于 2008-10-24 只看该作者 举报 回复 引用
麦克斯韦提出的涡旋电场和位移电流假说的核心思想是：变化的磁场可以激发涡旋电场，变化的电场可以激发涡旋磁场；电场和磁场不是彼此孤立的，它们相互联系、相互激发组成一个统一的电磁场。麦克斯韦进一步将电场和磁场的所有规律综合起来，建立了完整的电磁场理论体系。这个电磁场理论体系的核心就是麦克斯韦方程组。 p`l0?^r c"
麦克斯韦方程组积分形式 ;cQ6g` bM
zRyuq1Zyc,
其中：（1）描述了电场的性质。在一般情况下，电场可以是库仑电场也可以是变化磁场激发的感应电场，而感应电场是涡旋场，它的电位移线是闭合的，对封闭曲面的通量无贡献。 UX dUO@
（2）描述了磁场的性质。磁场可以由传导电流激发，也可以由变化电场的位移电流所激发，它们的磁场都是涡旋场，磁感应线都是闭合线，对封闭曲面的通量无贡献。 ?: ) ]h c
（3）描述了变化的磁场激发电场的规律。 CO`_^7 o9(
（4）描述了变化的电场激发磁场的规律。 o |$AyS {1
变化场与稳恒场的关系： 9o+)?1
当
Wr( y)D 方程组就还原为静电场和稳恒磁场的方程： Jl&- , V*****
* cgI. +
V b= Mg
在没有场源的自由空间，即q=0, I=0，方程组就成为如下形式： {o>j6R S
麦克斯韦方程组的积分形式反映了空间某区域的电磁场量(D、E、B、H)和场源(电荷q、电流I)之间的关系。
4楼
cxw770
级别: 积极交流四级
显示用户信息 UID: 14900
精华: 0
发帖: 367
rf币: 753 个
威望: 0 点
技术分: 4 点
版主等级: 0 级
研究方向: HFSS
注册时间: 2008-07-07
最后登录: 2009-10-19 cxw770 发表于 2008-10-24 只看该作者 举报 回复 引用
麦克斯韦方程组微分形式：在电磁场的实际应用中，经常要知道空间逐点的电磁场量和电荷、电流之间的关系。从数学形式上，就是将麦克斯韦方程组的积分形式化为微分形式。利用矢量分析方法，可得： 3 ~ S8!nx
[ji#U s:h
Q g [/%$x.
注意：(1)在不同的惯性参照系中，麦克斯韦方程有同样的形式。 2L} SJU k*
(2) 应用麦克斯韦方程组解决实际问题，还要考虑介质对电磁场的影响。例如在各向同性介质中，电磁场量与介质特性量有下列关系： b+&% 1C
X .5aMm
jgZ ;_! W
I$ 0)Px% z
在非均匀介质中，还要考虑电磁场量在界面上的边值关系。在利用t=0时场量的初值条件，原则上可以求出任一时刻空间任一点的电磁场，即E(x,y,z,t)和B(x,y,z,t)。 #[ `: 'e
麦克斯韦方程组揭示了电场与磁场相互转化中产生的对称性优美，这种优美以现代数学形式得到充分的表达。但是，我们一方面应当承认，恰当的数学形式才能充分展示经验方法中看不到的整体性(电磁对称性)，但另一方面，我们也不应当忘记，这种对称性的优美是以数学形式反映出来的电磁场的统一本质。因此我们应当认识到应在数学的表达方式中"发现"或"看出" 了这种对称性，而不是从物理数学公式中直接推演出这种本质。
5楼
cxw770
级别: 积极交流四级
显示用户信息 UID: 14900
精华: 0
发帖: 367
rf币: 753 个
威望: 0 点
技术分: 4 点
版主等级: 0 级
研究方向: HFSS
注册时间: 2008-07-07
最后登录: 2009-10-19 cxw770 发表于 2008-10-24 只看该作者 举报 回复 引用
Maxwell方程与电磁波
附件: 電磁理论.pdf (116 K) 下载次数:29
6楼
cem-uestc
级别: 首席版主
显示用户信息 UID: 9061
精华: 4
发帖: 2391
rf币: 4315 个
威望: 45 点
技术分: 653 点
版主等级: 21 级
研究方向: 数值计算
注册时间: 2008-03-07
最后登录: 2010-05-31
cem-uestc 发表于 2008-10-25 只看该作者 举报 回复 引用
两个旋度方程是根据实验得来的安培公式、法拉第公式，通过矢量算子理论在数学上化解等价得到的，再根据方程的对称性假设位移电流项的存在，得到MaxWell方程。
简单来说，前面两个叉乘表示 ：电场的空间变化会引起磁场的时间变化，磁场的空间变化会引起电场的时间变化。同时看出传播方向与电磁场方向垂直，所以电磁波是个横波。 l U$0e0 9
后面两个点乘 表示H和D在边界不能突变，是连续的。
逆流而上
高斯磁定律：
;
是渦胞的質量密度，對應於磁導率，、、分別為渦胞的週邊速度向量的三個投影於x-軸、y-軸和z-軸的分量，對應於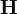的三個分量。色散或吸收：
和是頻率的函數。因果論不允許物質具有非色散性，例如，克拉莫-克若尼關係式。場與場之間的相位可能不同相，這導致和為複值，也導致電磁波被物質吸收[20]。：彎曲時空中的麦克斯韦方程组
物質和能量會造成時空彎曲。這是廣義相對論的主題。時空彎曲會影響電動力學的物理。一個電磁場所擁有的能量和動量也會造成時空彎曲。將平直時空的方程組中的偏導數，替換為協變導數，就可以得到彎曲時空中的馬克士威方程組。採用高斯單位制，馬克士威方程組表達為
、
；
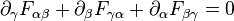是表徵時空彎曲的克里斯托費爾符號。1
麦克斯韦方程组在动态时空中的非线性[编辑]
在考虑麦克斯韦方程组本身与背景时空无关时，时空度规在广义相对论中被认为是受电磁场影响的动态变化的变量，这导致了电磁波方程和麦克斯韦方程组是非线性的。这一点可以从爱因斯坦场方程中的曲率张量依赖于应力-能量张量看出。
是万有引力常数， （标量曲率）是里奇张量的迹。应力-能量张量来源于粒子的应力和能量，但同时也来源于电磁场，这造就了非线性。若你的场是一个流速场,则该场的散度是该流体在某一点单位时间流出单 O(D2F $VlL
位体积的净流量. 如果在某点,某场的散度不为零,表示该场在该点有源, Sw5-^2x 0'
例如若电场在某点散度不为零,表示该点有电荷,若流速场不为零,表是在 T5.^ w
该点有流体源源不绝地产生或消失(若散度为负). 这一点也不难理解,你 3hUP > F8
把Gauss's law写下来就明白这是什么意思了. |' ) P Q
rK:cUW0]X
旋度告诉你的是,一个场在某处,沿着一无穷小的平面边界做环积分,平 2' ^ 7G@%
面法向量即由旋度向量给定,旋度向量的长度则是单位面积的环积分值. K' <[kh:cl
基本上旋度要衡量的是一向量场在某点是否有转弯. 这件事只要你把 CXyb 8z4/+
Stoke's law写下来就一清二处了....
2楼
gwzhao
找了一个描述比较系统的给你看看。 @!" ) shc
麦克斯韦方程组 |/K| Vw a
关于静电场和稳恒磁场的基本规律，可总结归纳成以下四条基本定理： )(G<(e iD
静电场的高斯定理： #k9 &OS?
静电场的环路定理： PFp!T [)
稳恒磁场的高斯定理： TQO |C?
磁场的安培环路定理： W Pd : t
上述这些定理都?****铝⒌馗?隽司驳绯『臀群愦懦〉墓媛桑?员浠?绯『捅浠?懦〔⒉皇视谩?span style="display:none"> yn A_Z ^j
I ? D=Q $s
麦克斯韦在稳恒场理论的基础上，提出了涡旋电场和位移电流的概念： 3 Y#
1. 麦克斯韦提出的涡旋电场的概念，揭示出变化的磁场可以在空间激发电场，并通过法拉第电磁感应定律得出了二者的关系，公式表明，任何随时间而变化的磁场，都是和涡旋电场联系在一起的。 kKF=%J ?X
2. 麦克斯韦提出的位移电流的概念，揭示出变化的电场可以在空间激发磁场，并通过全电流概念的引入，得到了一般形式下的安培环路定理在真空或介质中的表示形式，公式表明，任何随时间而变化的电场，都是和磁场联系在一起的。 - I{op wd
综合上述两点可知，变化的电场和变化的磁场彼此不?****铝⒌模??怯涝睹芮械亓?翟谝黄穑?嗷ゼしⅲ?槌梢桓鐾骋坏牡绱懦〉恼?濉Ｕ饩褪锹罂怂刮さ绱懦±砺鄣幕?靖拍睢?span style="display:none"> C L2zZk{u_
R }I4'
在麦克斯韦电磁场理论中，自由电荷可激发电场 ，变化磁场也可激发电场 ，则在一般情况下，空间任一点的电场强度应该表示为 H 2 I
又由于，稳恒电流可激发磁场 ，变化电场也可激发磁场 。 4}D&=0 I Z
因此，在一般情况下，电磁场的基本规律中，应该既包含稳恒电、磁场的规律，也包含变化电磁场的规律， C4E }.``Hm
M#2<|VUW,
根据麦克斯韦提出的涡旋电场和位移电流的概念，变化的磁场可以在空间激发变化的涡旋电场，而变化的电场也可以在空间激发变化的涡旋磁场。因此，电磁场可以在没有自由电荷和传导电流的空间单独存在。变化电磁场的规律是： ;gEEdx'&T
1.电场的高斯定理 在没有自由电荷的空间，由变化磁场激发的涡旋电场的电场线是一系列的闭合曲线。通过场中任何封闭曲面的电位移通量等于零。 ]z7 pa^
2.电场的环路定理。 n Zj&Ma 7R
3.磁场的高斯定理 变化的电场产生的磁场和传导电流产生的磁场相同，都是涡旋状的场，磁感线是闭合线。因此，磁场的高斯定理仍适用。 ?_{ {ii l
4.磁场的安培环路定。 8 5"Sz c-#
umPN=0u6
-;Mh |!y g
在变化电磁场的上述规律中，电场和磁场成为不可分割的一个整体。 O:V. ;q2]U
_JpTHpqu
将两种电、磁场的规律合并在一起，就得到电磁场的基本规律，称之为麦克斯韦方程组。 # ( 4 )ps.
'u PI~l`g
上面四个方程可逐一说明如下：在电磁场中任一点处 1(aib ^!B
（1）电位移的散度 等于该点处自由电荷的体密度 ； sAX4giaL D
（2）电场强度的旋度 等于该点处磁感强度变化率 的负值； B_c-@kl
（3）磁场强度的旋度 等于该点处传导电流密度 与位移电流密度 的矢量和； 4 ti Cx f)
（4）磁感强度的散度 处处等于零。 >4lA +1JYk
麦克斯韦方程是宏观电磁场理论的基本方程，在具体应用这些方程时，还要考虑到介质特性对电磁场的影响， )1 0 aDTlr
以及欧姆定律的微分形式 。 pkIJbI{aS
]x_ 1 4$rk
方程组的微分形式，通常称为麦克斯韦方程。 g e pY V}
G n qun %
在麦克斯韦方程组中，电场和磁场已经成为一个不可分割的整体。该方程组系统而完整地概括了电磁场的基本规律，并预言了电磁波的存在。
逆流而上
3楼
cxw770
级别: 积极交流四级
显示用户信息 UID: 14900
精华: 0
发帖: 367
rf币: 753 个
威望: 0 点
技术分: 4 点
版主等级: 0 级
研究方向: HFSS
注册时间: 2008-07-07
最后登录: 2009-10-19 cxw770 发表于 2008-10-24 只看该作者 举报 回复 引用
麦克斯韦提出的涡旋电场和位移电流假说的核心思想是：变化的磁场可以激发涡旋电场，变化的电场可以激发涡旋磁场；电场和磁场不是彼此孤立的，它们相互联系、相互激发组成一个统一的电磁场。麦克斯韦进一步将电场和磁场的所有规律综合起来，建立了完整的电磁场理论体系。这个电磁场理论体系的核心就是麦克斯韦方程组。 p`l0?^r c"
麦克斯韦方程组积分形式 ;cQ6g` bM
zRyuq1Zyc,
其中：（1）描述了电场的性质。在一般情况下，电场可以是库仑电场也可以是变化磁场激发的感应电场，而感应电场是涡旋场，它的电位移线是闭合的，对封闭曲面的通量无贡献。 UX dUO@
（2）描述了磁场的性质。磁场可以由传导电流激发，也可以由变化电场的位移电流所激发，它们的磁场都是涡旋场，磁感应线都是闭合线，对封闭曲面的通量无贡献。 ?: ) ]h c
（3）描述了变化的磁场激发电场的规律。 CO`_^7 o9(
（4）描述了变化的电场激发磁场的规律。 o |$AyS {1
变化场与稳恒场的关系： 9o+)?1
当
Wr( y)D
* cgI. +
V b= Mg
在没有场源的自由空间，即q=0, I=0，方程组就成为如下形式： {o>j6R S
麦克斯韦方程组的积分形式反映了空间某区域的电磁场量(D、E、B、H)和场源(电荷q、电流I)之间的关系。
4楼
cxw770
级别: 积极交流四级
显示用户信息 UID: 14900
精华: 0
发帖: 367
rf币: 753 个
威望: 0 点
技术分: 4 点
版主等级: 0 级
研究方向: HFSS
注册时间: 2008-07-07
最后登录: 2009-10-19 cxw770 发表于 2008-10-24 只看该作者 举报 回复 引用
麦克斯韦方程组微分形式：在电磁场的实际应用中，经常要知道空间逐点的电磁场量和电荷、电流之间的关系。从数学形式上，就是将麦克斯韦方程组的积分形式化为微分形式。利用矢量分析方法，可得： 3 ~ S8!nx
[ji#U s:h
Q g [/%$x.
注意：(1)在不同的惯性参照系中，麦克斯韦方程有同样的形式。 2L} SJU k*
(2) 应用麦克斯韦方程组解决实际问题，还要考虑介质对电磁场的影响。例如在各向同性介质中，电磁场量与介质特性量有下列关系： b+&% 1C
X .5aMm
jgZ ;_! W
I$ 0)Px% z
在非均匀介质中，还要考虑电磁场量在界面上的边值关系。在利用t=0时场量的初值条件，原则上可以求出任一时刻空间任一点的电磁场，即E(x,y,z,t)和B(x,y,z,t)。 #[ `: 'e
麦克斯韦方程组揭示了电场与磁场相互转化中产生的对称性优美，这种优美以现代数学形式得到充分的表达。但是，我们一方面应当承认，恰当的数学形式才能充分展示经验方法中看不到的整体性(电磁对称性)，但另一方面，我们也不应当忘记，这种对称性的优美是以数学形式反映出来的电磁场的统一本质。因此我们应当认识到应在数学的表达方式中"发现"或"看出" 了这种对称性，而不是从物理数学公式中直接推演出这种本质。
5楼
cxw770
级别: 积极交流四级
显示用户信息 UID: 14900
精华: 0
发帖: 367
rf币: 753 个
威望: 0 点
技术分: 4 点
版主等级: 0 级
研究方向: HFSS
注册时间: 2008-07-07
最后登录: 2009-10-19 cxw770 发表于 2008-10-24 只看该作者 举报 回复 引用
Maxwell方程与电磁波
附件: 電磁理论.pdf (116 K) 下载次数:29
6楼
cem-uestc
级别: 首席版主
显示用户信息 UID: 9061
精华: 4
发帖: 2391
rf币: 4315 个
威望: 45 点
技术分: 653 点
版主等级: 21 级
研究方向: 数值计算
注册时间: 2008-03-07
最后登录: 2010-05-31
cem-uestc 发表于 2008-10-25 只看该作者 举报 回复 引用
两个旋度方程是根据实验得来的安培公式、法拉第公式，通过矢量算子理论在数学上化解等价得到的，再根据方程的对称性假设位移电流项的存在，得到MaxWell方程。
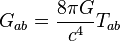
No comments:
Post a Comment