tiantianlu02 于 2013-12-27 15:10:56 [档案] [博客] [旧帖] [给我悄悄话] 本文已被阅读: 2125 次 (3378 bytes)
本文内容已被 [ tiantianlu02 ] 在 2013-12-28 00:01:11 编辑过。如有问题,请报告版主或论坛管理删除.
今天看到一个关于addiction和神经递质(neurotransmitters)关系的简介。虽然一般所说的上瘾是指由药物,毒品诱发的依赖性行为,但觉得对赌博和玩游戏的过度迷恋也相似之处。不知道神经科学对后者的研究有没有类似的结论。
文中说上瘾一般受三个因素的影响:基因,环境和压力。与三种神经递质有关:羟色胺(serotonin),多巴胺(dopamine)和正肾上腺素 (noradrenalin)。羟色胺可以调节人的情绪和感情,缺少羟色胺会导致抑郁或迷恋,以及人的强迫行为。多巴胺又称“快乐物质”。我们在经历快乐的感觉时,多巴胺会释放到大脑的依伏神经核,这是负责奖赏,快乐的中心,然后进入记忆中心,记忆中心然后激活行为中心来重复这一经历。神经的奖赏通道就是建立在重复的快乐经历上, 越快乐的经历越被重复,奖赏通道越强大,大脑也越想要重复同样的经历。正肾上腺素是人体应付恐惧和威胁的荷尔蒙。文中说每个人的基因决定了这三种递质关系的分布是否平衡。对什么东西上瘾多半跟哪一种神经递质失调有关。压力引起的内分泌失调也会触发神经递质的失衡。
孩子在前青春期和青春期的荷尔蒙分泌比较旺盛,对有些孩子来说,游戏很可能是导致这些神经递质失衡的一个外界的诱因。有的父母对孩子玩游戏上瘾的恐惧不完全是毫无根据的。也不是每个孩子都能自我调节和控制自己的行为。父母在担心之余可以考虑以其他活动来调节孩子的行为,比如体育运动可以帮助分泌羟色胺(serotonin)和多巴胺(dopamine),孩子就不需要单单依靠从游戏中来获取快乐了
真空里面有什么? 这绝不是一个平凡的问题. 某种程度上说, 几乎整个二十世纪, (高能)物理学家们都在寻找这个问题的答案.
 .
.
他发现这个方程的解总是成对存在: 如果 是这个方程能量为
是这个方程能量为 的粒子的解, 那么也存在一个对应的能量为
的粒子的解, 那么也存在一个对应的能量为 的粒子的解
的粒子的解 . 所谓真空, 是系统能量最低的状态. 现在问题来了,
. 所谓真空, 是系统能量最低的状态. 现在问题来了,  的能量是负的, 那么为了达到真空, 一个处于正能态电子将会放出能量(比如通过与电磁场耦合, 放出电磁辐射)达到负能态, 然后继续放出能量, 最终达到
的能量是负的, 那么为了达到真空, 一个处于正能态电子将会放出能量(比如通过与电磁场耦合, 放出电磁辐射)达到负能态, 然后继续放出能量, 最终达到 的真空.
的真空.
上面的论断显然是荒谬的. 在现实生活中, 我们从来没有见过一个电子辐射出无穷多的能量. Dirac 提出了一个天才的解释: 电子是1/2自旋粒子, 服从 Pauli 不相容原理. 如果所有负能态都已经被电子完全占据了, 那么 Pauli 不相容原理就可以阻止处于正能态的电子进入负能态的海洋. 因此在 Dirac 的理论中, 真空不是什么都没有, 而是充满了负能态的电子(以及其他自旋1/2粒子)!
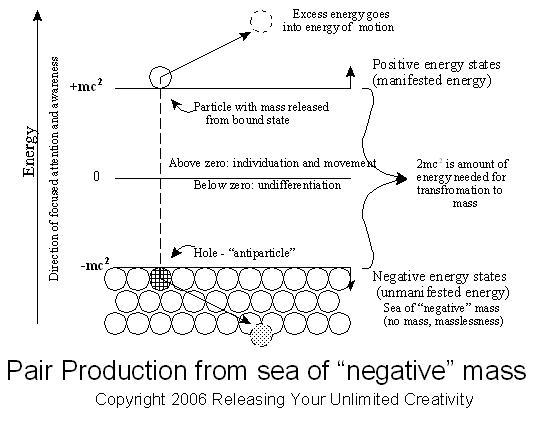
这个理论最大的成功之处在于其对正电子的成功预言: 如果由于某些原因, 电子海中的一个能量为 电子离开了电子海, 在电子海中留下了一个空穴. 那么一个能量为
电子离开了电子海, 在电子海中留下了一个空穴. 那么一个能量为 的正能态电子将会填上这个空穴, 并发出能量
的正能态电子将会填上这个空穴, 并发出能量 , 使系统重新回到真空:
, 使系统重新回到真空:
 .
.
那么空穴等效地拥有一个正电荷 以及正能量. 这个空穴就是所谓正电子, 它是电子的反粒子. 在 Dirac 方程提出后的第二年, 1929年, 实验物理学家们就在云室里发现了正电子的踪迹. Dirac 的方程成功预言了所有自旋1/2粒子都存在反粒子.
以及正能量. 这个空穴就是所谓正电子, 它是电子的反粒子. 在 Dirac 方程提出后的第二年, 1929年, 实验物理学家们就在云室里发现了正电子的踪迹. Dirac 的方程成功预言了所有自旋1/2粒子都存在反粒子.
(有意思的是, 尽管我说 Dirac 电子海的理论最大的成功之处在于其对正电子的成功预言. 在这个理论刚提出时, Dirac 一直以为电子海中空穴是质子, 而不是正电子. )
物理学家们对 Dirac 的理论也确实不满意. 1930年以后, 物理学家们发展出了一套新的理论: 量子场论. 在这个新的理论框架下, Dirac 方程依然成立. 但此时它的物理意义不再是一个单粒子方程, 而是一个场方程. 不再是波函数, 而是像电磁场一样的场. 在这种新的解读下, 真空不再是电子海, 正电子也不再是"电子海中的空穴", 而确确实实是一个实物粒子. 恼人的负能量也随之消失. 量子场论中只有正能量! 哈哈~
不再是波函数, 而是像电磁场一样的场. 在这种新的解读下, 真空不再是电子海, 正电子也不再是"电子海中的空穴", 而确确实实是一个实物粒子. 恼人的负能量也随之消失. 量子场论中只有正能量! 哈哈~
(但我个人认为, 场论中的这种做法只是在玩数学游戏, 将 Dirac 电子海换了一种说法. 背后的物理和 Dirac 的电子海没有本质不同. )
但量子场论没能解决真空能量为负无穷的问题. 因为这实际上是量子场所固有的性质, 或者说, 是由场的波动性所导致的必然结果. 学过量子力学课程的人一定会记得非相对论量子力学中谐振子的能级为 , 其中
, 其中 是所谓真空零点能. 下面我们将会看到, 这是 Heisenberg 不确定性原理导致的结果:
是所谓真空零点能. 下面我们将会看到, 这是 Heisenberg 不确定性原理导致的结果:
谐振子的能量 .
.
Heisenberg 不确定性原理为: . 代入上式:
. 代入上式:
 .
.
根据均值不等式, 有 .
.
其物理解释为, Heisenberg 不确定性原理导致了任何量子力学系统都存在涨落, 包括真空. 在真空中, 这一涨落体现为零点能.
由于一个量子场的自由度是无穷大的, 相当于空间中每一点都有这样一个谐振子. 这无穷多个谐振子的零点能相加导致了量子场的零点能发散.
(其实零点能发散并不是一个那么严重的问题. 因为我们并不能直接测量零点能, 而测量的是任何能量与零点能的差值. )
之前说到真空中存在量子涨落, 还有无穷大的零点能. 我们能否在实验上验证这一点? 毕竟一个物理学理论正确与否, 关键就在于它能否经得起实验的考验. 答案是肯定的.
我们在真空中放三块板, 它们之间的距离如下图所示.
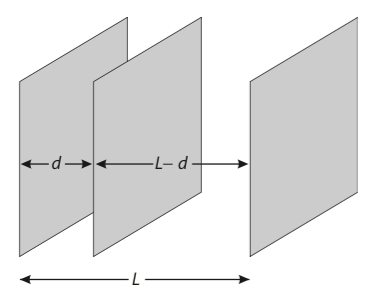 真空的能量为谐振子的零点能. 这里的谐振子为板之间的振动模式:
真空的能量为谐振子的零点能. 这里的谐振子为板之间的振动模式:  , 对应的频率为
, 对应的频率为 . 这是由真空中的场在板的边界处振幅为零的边界条件所得到的.
. 这是由真空中的场在板的边界处振幅为零的边界条件所得到的.
因此系统的零点能
 . 其中
. 其中 .
.
上面就出现了对所有自然数的求和. 它显然是发散的. 发散的原因是我们对所有的振动模式求和的缘故. 但由于板在物理上不可能以任意高的频率振动, 因此为了得到物理的结果, 我们必须对求和做截断. 在 自然数之和是多少? - andrew shen 的回答 中, 我引入了一个 的"权重因子". 当
的"权重因子". 当 时, "权重因子"趋于零. "权重因子"确实可以起到截断高频振动的效果.
时, "权重因子"趋于零. "权重因子"确实可以起到截断高频振动的效果.
引入权重因子之后的计算结果为:
当 时,
时,  发散. 这是因为
发散. 这是因为 就相当于没有权重因子. 中间的板所感受到的力应当为:
就相当于没有权重因子. 中间的板所感受到的力应当为:  .
.
取 的极限, 消除权重因子的作用, 我们发现板感受到的力为有限值:
的极限, 消除权重因子的作用, 我们发现板感受到的力为有限值:  . 当
. 当 时, 力简化为
时, 力简化为 .
.
这是一个吸引力. 实验物理学家们的测量表明真空中的两个板之间确实存在这样的吸引力. 我们并没有假设板之间存在任何直接的相互作用. 这个吸引力完全是由板之间的真空导致的.
比如我们知道原子在电磁场中有: 受激辐射, 受激吸收, 自发辐射 这三个现象. 其中自发辐射说的是, 在没有任何外界作用下, 激发态原子的电子自发地从高能级向低能级跃迁, 同时发射出一个能量为 的光子.
的光子.
这粗看起来与量子力学的基本原理相违背. 量子力学告诉我们, 当电子处于原子的某一能级时, 是能量本征态. 在没有外界作用时, 电子将永远处于这个能量本征态. 量子力学基本原理应该是不会出错的, 那究竟是什么使电子自发向低能级跃迁呢?
是真空. 是真空中的量子涨落与电子发生了相互作用, 这个涨落带来的扰动使原子向低能级跃迁. (用场论的语言说, 是真空中的涨落产生了虚光子. 尽管我尽量避免使用虚粒子的语言. 因为它容易给初学者带来困惑. )
到这里你也许会问: 咦? 以太复活了? 我想在某种程度上, 是的. 引用豆瓣物理组组长 E 大的一段话:
几点注记:
真空里面有什么? 这绝不是一个平凡的问题. 某种程度上说, 几乎整个二十世纪, (高能)物理学家们都在寻找这个问题的答案.
- Dirac 的电子海
他发现这个方程的解总是成对存在: 如果
上面的论断显然是荒谬的. 在现实生活中, 我们从来没有见过一个电子辐射出无穷多的能量. Dirac 提出了一个天才的解释: 电子是1/2自旋粒子, 服从 Pauli 不相容原理. 如果所有负能态都已经被电子完全占据了, 那么 Pauli 不相容原理就可以阻止处于正能态的电子进入负能态的海洋. 因此在 Dirac 的理论中, 真空不是什么都没有, 而是充满了负能态的电子(以及其他自旋1/2粒子)!
这个理论最大的成功之处在于其对正电子的成功预言: 如果由于某些原因, 电子海中的一个能量为
那么空穴等效地拥有一个正电荷
(有意思的是, 尽管我说 Dirac 电子海的理论最大的成功之处在于其对正电子的成功预言. 在这个理论刚提出时, Dirac 一直以为电子海中空穴是质子, 而不是正电子. )

- 真空零点能
物理学家们对 Dirac 的理论也确实不满意. 1930年以后, 物理学家们发展出了一套新的理论: 量子场论. 在这个新的理论框架下, Dirac 方程依然成立. 但此时它的物理意义不再是一个单粒子方程, 而是一个场方程.
(但我个人认为, 场论中的这种做法只是在玩数学游戏, 将 Dirac 电子海换了一种说法. 背后的物理和 Dirac 的电子海没有本质不同. )
但量子场论没能解决真空能量为负无穷的问题. 因为这实际上是量子场所固有的性质, 或者说, 是由场的波动性所导致的必然结果. 学过量子力学课程的人一定会记得非相对论量子力学中谐振子的能级为
谐振子的能量
Heisenberg 不确定性原理为:
根据均值不等式, 有
其物理解释为, Heisenberg 不确定性原理导致了任何量子力学系统都存在涨落, 包括真空. 在真空中, 这一涨落体现为零点能.
由于一个量子场的自由度是无穷大的, 相当于空间中每一点都有这样一个谐振子. 这无穷多个谐振子的零点能相加导致了量子场的零点能发散.
(其实零点能发散并不是一个那么严重的问题. 因为我们并不能直接测量零点能, 而测量的是任何能量与零点能的差值. )
- 从自然数之和是多少?到 Casimir 效应
之前说到真空中存在量子涨落, 还有无穷大的零点能. 我们能否在实验上验证这一点? 毕竟一个物理学理论正确与否, 关键就在于它能否经得起实验的考验. 答案是肯定的.
我们在真空中放三块板, 它们之间的距离如下图所示.
 真空的能量为谐振子的零点能. 这里的谐振子为板之间的振动模式:
真空的能量为谐振子的零点能. 这里的谐振子为板之间的振动模式: 因此系统的零点能
上面就出现了对所有自然数的求和. 它显然是发散的. 发散的原因是我们对所有的振动模式求和的缘故. 但由于板在物理上不可能以任意高的频率振动, 因此为了得到物理的结果, 我们必须对求和做截断. 在 自然数之和是多少? - andrew shen 的回答 中, 我引入了一个
引入权重因子之后的计算结果为:
当
取
这是一个吸引力. 实验物理学家们的测量表明真空中的两个板之间确实存在这样的吸引力. 我们并没有假设板之间存在任何直接的相互作用. 这个吸引力完全是由板之间的真空导致的.
- 原子的自发辐射现象
比如我们知道原子在电磁场中有: 受激辐射, 受激吸收, 自发辐射 这三个现象. 其中自发辐射说的是, 在没有任何外界作用下, 激发态原子的电子自发地从高能级向低能级跃迁, 同时发射出一个能量为
这粗看起来与量子力学的基本原理相违背. 量子力学告诉我们, 当电子处于原子的某一能级时, 是能量本征态. 在没有外界作用时, 电子将永远处于这个能量本征态. 量子力学基本原理应该是不会出错的, 那究竟是什么使电子自发向低能级跃迁呢?
是真空. 是真空中的量子涨落与电子发生了相互作用, 这个涨落带来的扰动使原子向低能级跃迁. (用场论的语言说, 是真空中的涨落产生了虚光子. 尽管我尽量避免使用虚粒子的语言. 因为它容易给初学者带来困惑. )
- A loose end
到这里你也许会问: 咦? 以太复活了? 我想在某种程度上, 是的. 引用豆瓣物理组组长 E 大的一段话:
把真空看成物质是早已存在的观念,而且以前还有个名字,那就是“以太”,现在我们叫它“量子场”。量子场论的出现,实际上意味着以太的复活,但是somehow在物理学共同内部,大家都保守着这个秘密。因为我们要对抗民科,民科是不会去touch量子场论的,这样以太就安全了。
几点注记:
- 如果你对固体物理有所了解, 就会发现 Dirac 的电子海图像在固体物理中有完美对应. 在半导体中, 价带被电子完全填满, 相当于 Dirac 的电子海, 而导带全空. 如果有电子从价带被激发至导带, 那么将会在价带中产生一个带正电荷的空穴.
- 实际上真空在物理学中也不是一个 well-defined 的概念. 在不同的能标下可能有不同的真空. 这里答主说的真空实际上很狭义地指 QED 真空. QCD 的真空有更丰富的物理, 但这已经超出了答主的能力范围.
- 有关 Casimir 效应答主参考了 A.Zee 的《Quantum Field Theory in a Nutshell》的 I.9 节.
- 答主并不是高能物理方向的. 上面所说难免有不准确之处.

No comments:
Post a Comment