干涉(interference)
干涉(interference)
國立臺灣大學物理博士班嚴治平
在介紹干涉(interference)之前,先介紹相位(phase)與疊加原理(superposition principle)!相位是波(wave)最重要的性質之一,而疊加原理則是處理數個波在時間、空間上重疊時的方法。
先以一維的繩波來介紹:
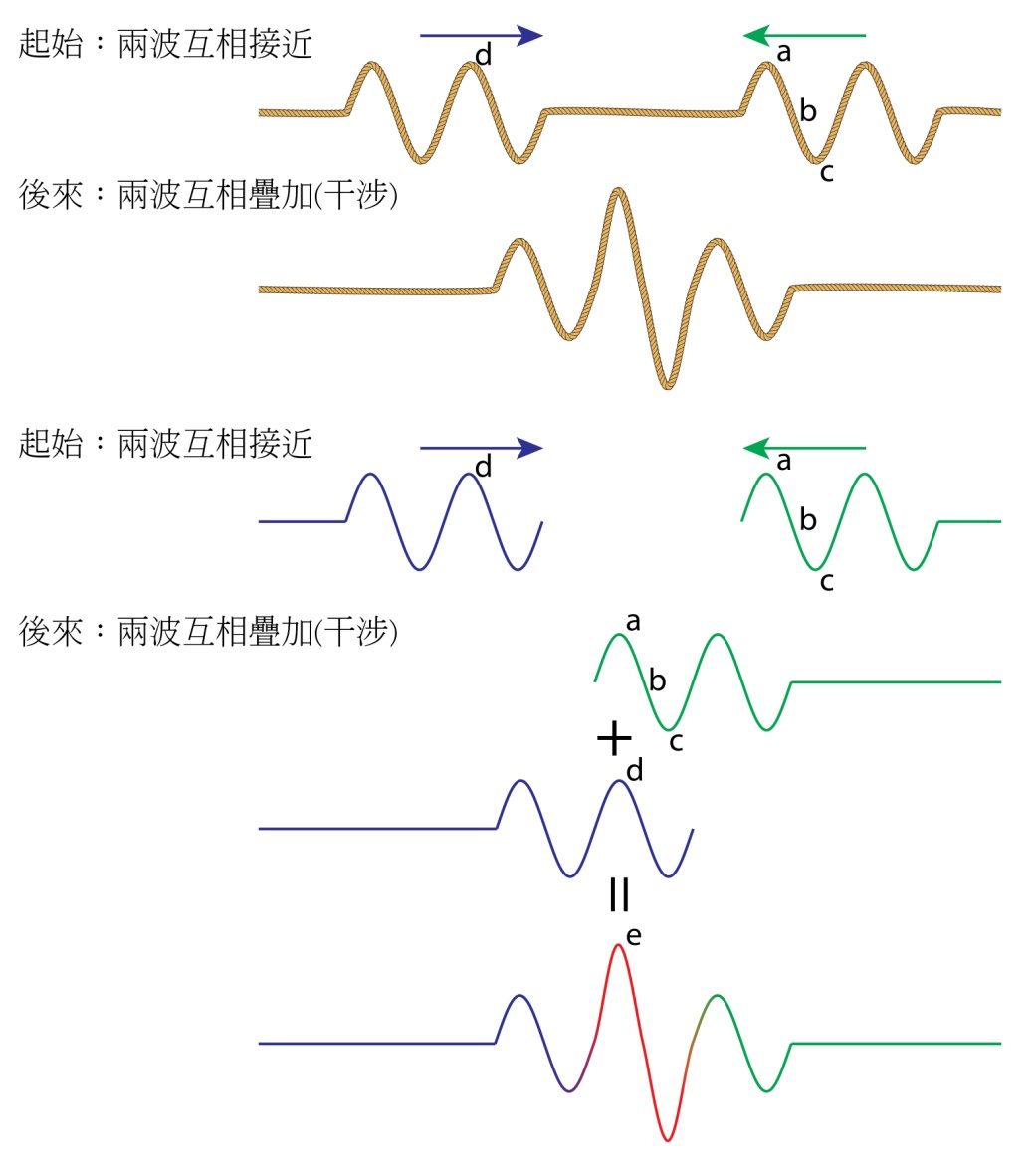
在同一條繩子上有兩個繩波相向而行(參見圖一),當兩波交會時,在交會處繩子的振動方式乍看之下似乎有點複雜,但其實並不然,因為只需把向左傳播的繩波跟向右傳播的繩波在相同位置的振動相加便可,這就是疊加原理。不論有幾個波重疊在相同的時間、空間,將各自的振動相加就可以得到總和的波。 當不同的波在空間的某處疊加在一起時,我們便說這些波在進行干涉。
那麼甚麼是相位(phase)呢?
簡單來說,相位就是繩波振動的狀態,我們可以稱圖一中的a、b與c點的振動狀態為波峰、平衡點與波谷。因為a、d兩點都在波峰,所以疊加波的振動位置會是e,而這種兩個波同在波峰或同在波谷的情況,稱做同相位(in phase)。在物理圖像上,波峰、平衡點、波谷就是一種相位。
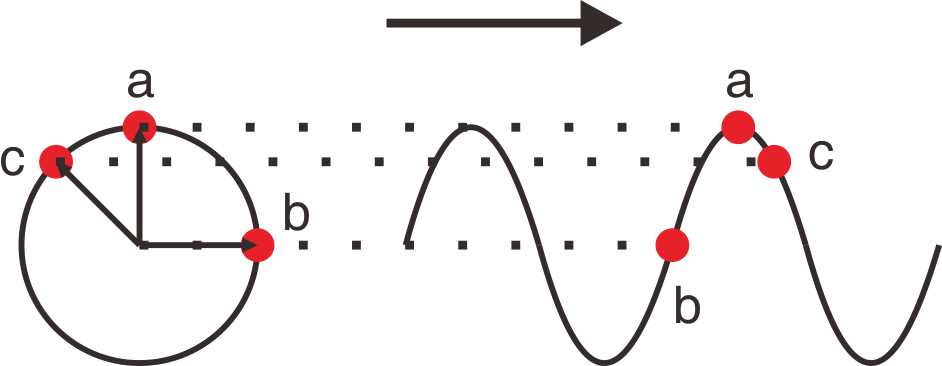
在數學的描述中,波可以利用圓周運動的投影來對比,圓周運動的角度就被當作波的相位(圖二)。在圖二中,ab的夾角為90度,cb的夾角為135度,若b的相位為0,則a、c的相位為π/2、3π/4。這種類比另一個有意思的地方在於,從圓周運動的投影可以直接獲知波動隨空間變化的關係:從三角函數可以知道,圓周運動在y軸的投影量為R*sin(θ),θ為箭頭與x方向的夾角,R為圓周半徑。
至於相位(θ)的數學形式,可以從三角函數的性質 得到:ba的距離是λ/4,cb的距離是λ3/8,對應的相位是π/2、3π/4。所以θ=2πx/λ,x為位置。所以波動隨空間變化的關係為R*sin(2πx/λ),其中R是振幅,x是位置,λ是波長。
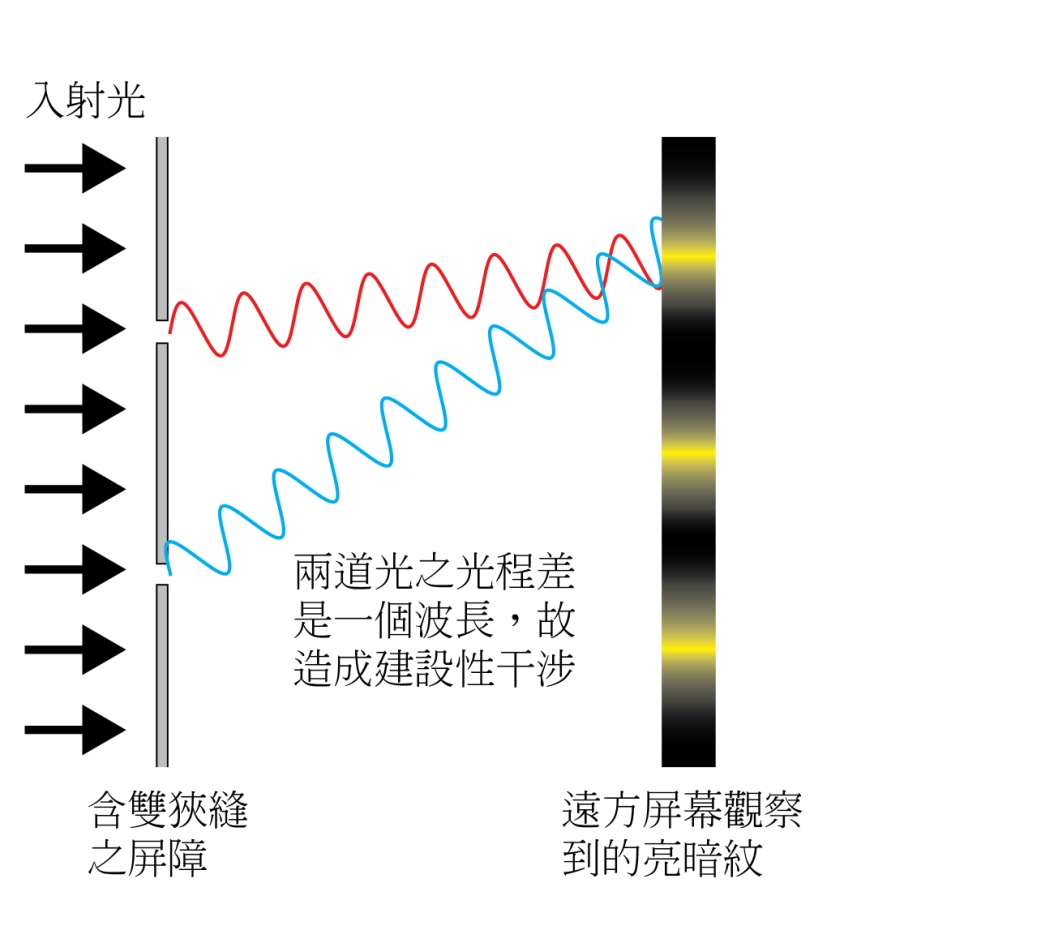
在利用一維的繩波說明相位、疊加原理與干涉後,來看看可見光的雙狹縫干涉吧!為方便計,假設使用的雷射是單一波長,且干涉條紋亮暗紋間距遠小於狹縫到屏幕的距離。從繩波的例子可以看出:建設性干涉發生在當波峰對波峰、波谷對波谷的情況,此時圖三中的兩道光之光程差是半波長的偶數倍,而破壞性干涉的條件為光程差是半波長的奇數倍。然而,在實際的情況中,因為雙狹縫干涉跟單狹縫繞射是同時發生的,所以真正觀察到的影像會是在單狹縫繞射的亮紋中,出現很多雙狹縫干涉的條紋(圖四)。
較有趣的現象是:類似的情況也會出現在物質波中。當電子經過雙狹縫時,干涉條紋也可以利用上述準確描述。在圖五中,利用底片接收經過雙狹縫的電子,可以發現隨著電子的數量越來越多,雙狹縫干涉條紋也越來越明顯。又因電子被底片記錄的物理機制為粒子性的物理效應,此干涉條紋顯示,每顆電子在經過光狹縫時都跟自己干涉。
國立臺灣大學物理博士班嚴治平
在介紹干涉(interference)之前,先介紹相位(phase)與疊加原理(superposition principle)!相位是波(wave)最重要的性質之一,而疊加原理則是處理數個波在時間、空間上重疊時的方法。
先以一維的繩波來介紹:
在同一條繩子上有兩個繩波相向而行(參見圖一),當兩波交會時,在交會處繩子的振動方式乍看之下似乎有點複雜,但其實並不然,因為只需把向左傳播的繩波跟向右傳播的繩波在相同位置的振動相加便可,這就是疊加原理。不論有幾個波重疊在相同的時間、空間,將各自的振動相加就可以得到總和的波。 當不同的波在空間的某處疊加在一起時,我們便說這些波在進行干涉。
那麼甚麼是相位(phase)呢?
簡單來說,相位就是繩波振動的狀態,我們可以稱圖一中的a、b與c點的振動狀態為波峰、平衡點與波谷。因為a、d兩點都在波峰,所以疊加波的振動位置會是e,而這種兩個波同在波峰或同在波谷的情況,稱做同相位(in phase)。在物理圖像上,波峰、平衡點、波谷就是一種相位。
在數學的描述中,波可以利用圓周運動的投影來對比,圓周運動的角度就被當作波的相位(圖二)。在圖二中,ab的夾角為90度,cb的夾角為135度,若b的相位為0,則a、c的相位為π/2、3π/4。這種類比另一個有意思的地方在於,從圓周運動的投影可以直接獲知波動隨空間變化的關係:從三角函數可以知道,圓周運動在y軸的投影量為R*sin(θ),θ為箭頭與x方向的夾角,R為圓周半徑。
至於相位(θ)的數學形式,可以從三角函數的性質 得到:ba的距離是λ/4,cb的距離是λ3/8,對應的相位是π/2、3π/4。所以θ=2πx/λ,x為位置。所以波動隨空間變化的關係為R*sin(2πx/λ),其中R是振幅,x是位置,λ是波長。
在利用一維的繩波說明相位、疊加原理與干涉後,來看看可見光的雙狹縫干涉吧!為方便計,假設使用的雷射是單一波長,且干涉條紋亮暗紋間距遠小於狹縫到屏幕的距離。從繩波的例子可以看出:建設性干涉發生在當波峰對波峰、波谷對波谷的情況,此時圖三中的兩道光之光程差是半波長的偶數倍,而破壞性干涉的條件為光程差是半波長的奇數倍。然而,在實際的情況中,因為雙狹縫干涉跟單狹縫繞射是同時發生的,所以真正觀察到的影像會是在單狹縫繞射的亮紋中,出現很多雙狹縫干涉的條紋(圖四)。
較有趣的現象是:類似的情況也會出現在物質波中。當電子經過雙狹縫時,干涉條紋也可以利用上述準確描述。在圖五中,利用底片接收經過雙狹縫的電子,可以發現隨著電子的數量越來越多,雙狹縫干涉條紋也越來越明顯。又因電子被底片記錄的物理機制為粒子性的物理效應,此干涉條紋顯示,每顆電子在經過光狹縫時都跟自己干涉。



No comments:
Post a Comment