若一波的波峰與另一波的波谷同時到達一點(反相),則兩波對該點的影響相互抵消,稱為破壞性干涉
谐振子在边界不规范,在圆内部更加
[PDF]觀察與操縱固體表面原子
www.cuhk.edu.hk/ics/21c/issue/articles/025_94238.pdf
另一方面, 這種針的穩定性低, 所以. STM在掃描過程 ... 能, 而這可能性令粒子能穿透所謂勢壘 ... 由於晶體內部的三維對稱性在表面受破壞成為二維, 所以原子排列方式會 .... (111)晶面, 電子波只沿與表面平行的方向連動, 所以由於干涉而形成的駐波.腹線節線
腹線節線
國立臺灣大學物理系李宛儒
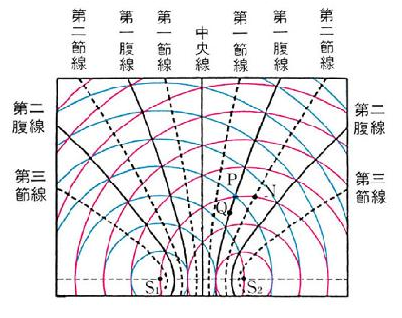
當兩個同調點波源互相干涉(Interference)時,會出現穩定的干涉圖形(如圖一),其中明暗交互出現的線條便是腹線(antinodal line)與節線(nodal line)。腹線與節線可在水波槽干涉實驗中被觀察。
波的干涉指的是兩個以上的波通過同樣的空間時,互相疊加產生新的波形。干涉遵守疊加原理(Principle of superposition),當不同波通過同一個空間時,空間中每一個點所受到的影響是所有波在該處造成的影響之總和,在許多場合中,不同的波之間可視為彼此不會影響。
涉可分為建設性干涉和破壞性干涉,由兩波在空間中該點的相位差決定。若兩波峰/波谷同時到達空間中的一點(同相),該點會有最大振幅,是為建設性干涉;相反地,若一波的波峰與另一波的波谷同時到達一點(反相),則兩波對該點的影響相互抵消,稱為破壞性干涉。 當兩個互相干涉波源所發射出來的波始終具有特定的相位關係時,稱之為同調波源。兩個同調波源干涉,則兩波在空間中任一點的相位差不隨時間改變,就會形成穩定的干涉圖形。
以兩同調之正弦波為例:

在二維平面中,產生完全建設性干涉/破壞性干涉的點會彼此連接,交互出現,形成腹線與節線(腹線為建設性干涉,節線為破壞性干涉)。平面中任一點到與兩波源之間的距離差是為波程差,當兩同調波源之間沒有相位差時,若波程差為波長的整數倍,則該點相位差為零,產生腹線;若波程差是波長整數倍再加上半波長,相位差恰好為180度,則會產生節線。在節線處由於破壞性干涉,看起來就如同沒有波通過一般。
腹線與節線的圖形是雙曲線,空間中任一點到固定兩點(波源)的距離差為定值所產生的曲線,正是雙曲線的定義。
以下為一個水波干涉的示意圖:
在兩波源中間,垂直於兩波源連線的中央線,實與腹線相同,為建設性干涉產生之處(波程差為零)。在中央現的兩邊,依序為第一節線、第一腹線、第二節線、第二腹線……
腹線與節線的數目由波長和波源間距決定。當nλ<1/2兩波源間距 d<(n+1)λ 時(λ:波長),兩側各會產生n 條腹線;當(n-1/2)λ <1/2 兩波源間距d<(n+1/2)λ 時,兩側各會產生n條節線。
數目又間接影響了腹線與節線的疏密:
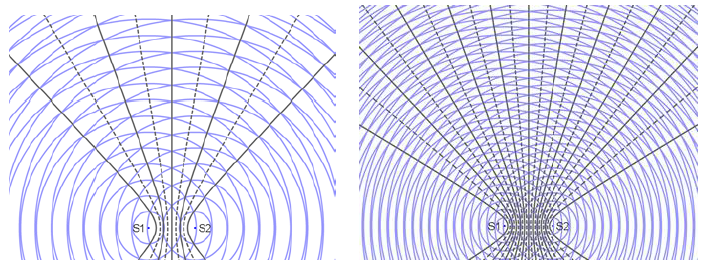
當波長較大時,腹線與節線數目較少,間距較大,波長較小時間距則較密集,如圖三所示。
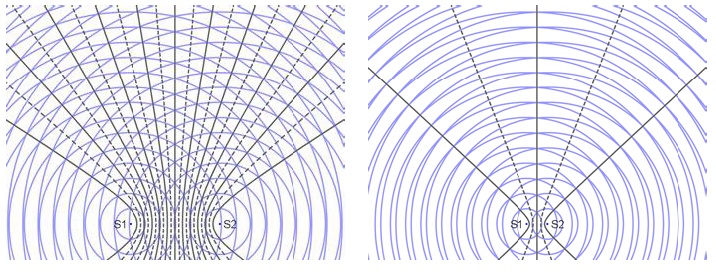
波源間距較大時,腹線與節線數目變多,會較密集,波源間距較小則較分開,如圖四所示。
參考資料:
1.維基百科:http://en.wikipedia.org/wiki/Interference_(wave_propagation)
2.D. Halliday, R. Resnick, and J. Walker, Principles of Physics, 9th ed., 2011.
3. 輿倫電子學習:http://developer.hanluninfo.com:8088/2005/hkcee/phy/chapter03/index_03_02_14_02.htm
國立臺灣大學物理系李宛儒
當兩個同調點波源互相干涉(Interference)時,會出現穩定的干涉圖形(如圖一),其中明暗交互出現的線條便是腹線(antinodal line)與節線(nodal line)。腹線與節線可在水波槽干涉實驗中被觀察。
波的干涉指的是兩個以上的波通過同樣的空間時,互相疊加產生新的波形。干涉遵守疊加原理(Principle of superposition),當不同波通過同一個空間時,空間中每一個點所受到的影響是所有波在該處造成的影響之總和,在許多場合中,不同的波之間可視為彼此不會影響。
涉可分為建設性干涉和破壞性干涉,由兩波在空間中該點的相位差決定。若兩波峰/波谷同時到達空間中的一點(同相),該點會有最大振幅,是為建設性干涉;相反地,若一波的波峰與另一波的波谷同時到達一點(反相),則兩波對該點的影響相互抵消,稱為破壞性干涉。 當兩個互相干涉波源所發射出來的波始終具有特定的相位關係時,稱之為同調波源。兩個同調波源干涉,則兩波在空間中任一點的相位差不隨時間改變,就會形成穩定的干涉圖形。
以兩同調之正弦波為例:

在二維平面中,產生完全建設性干涉/破壞性干涉的點會彼此連接,交互出現,形成腹線與節線(腹線為建設性干涉,節線為破壞性干涉)。平面中任一點到與兩波源之間的距離差是為波程差,當兩同調波源之間沒有相位差時,若波程差為波長的整數倍,則該點相位差為零,產生腹線;若波程差是波長整數倍再加上半波長,相位差恰好為180度,則會產生節線。在節線處由於破壞性干涉,看起來就如同沒有波通過一般。
腹線與節線的圖形是雙曲線,空間中任一點到固定兩點(波源)的距離差為定值所產生的曲線,正是雙曲線的定義。
以下為一個水波干涉的示意圖:
在兩波源中間,垂直於兩波源連線的中央線,實與腹線相同,為建設性干涉產生之處(波程差為零)。在中央現的兩邊,依序為第一節線、第一腹線、第二節線、第二腹線……
腹線與節線的數目由波長和波源間距決定。當nλ<1/2兩波源間距 d<(n+1)λ 時(λ:波長),兩側各會產生n 條腹線;當(n-1/2)λ <1/2 兩波源間距d<(n+1/2)λ 時,兩側各會產生n條節線。
數目又間接影響了腹線與節線的疏密:
當波長較大時,腹線與節線數目較少,間距較大,波長較小時間距則較密集,如圖三所示。
波源間距較大時,腹線與節線數目變多,會較密集,波源間距較小則較分開,如圖四所示。
參考資料:
1.維基百科:http://en.wikipedia.org/wiki/Interference_(wave_propagation)
2.D. Halliday, R. Resnick, and J. Walker, Principles of Physics, 9th ed., 2011.
3. 輿倫電子學習:http://developer.hanluninfo.com:8088/2005/hkcee/phy/chapter03/index_03_02_14_02.htm


No comments:
Post a Comment