周期结构有哪些呢?一维(线性)、二维(平面)和三维(空间)周期结构。关于波我们将它分成三类:标量波(例如电子运动的波函数)、矢量波(电磁波)、张量波(晶格波)。
【高等固体物理 笔记1】
||
在总结第一次和第二次上课的笔记之前,让我们思考一个问题:什么是物理学?当然这个问题问不同的人会有不同的答案,那么在这里我给出我自己的答案,供大家参考和拍砖。我认为的物理学是“考察自然界中物质的性质和演化的科学”。既然是物质,就一定会有组成和性质;既然是演化,就一定会有演化的规律。这两个问题基本涵盖了物理学中的绝大部分领域。也是我们下面整理的一个重点。
为什么我们要这么来做呢?毕竟高等固体物理这门课主要研究的是固体物理或者更广泛一点的凝聚态物理中物质的性质以及它们可能发生的演化方法。在物质性质中,我们比较常见的有:力学性质、热学性质、光学性质、电磁性质等等。而演化中往往是在一定条件下所进行的,因此我们要探究物质的演化规律。因此整个高等固体物理讲述的是这么一件事:“在凝聚态物理框架下探究物质的物理性质及系统演化规律的学科”。前面的废话先说到这里,下面让我们一起进入高等固体物理的课堂当中吧。
注1:因为下面所说的是笔记中的重新整理,可能叙述顺序可能与一般书本上的不太一样,当然这也带有了我个人的风格和理解在里面。我尽量把语言变得通俗一点,能不使用公式的地方尽量不适用ugly的大长串公式(一方面是为我个人方面,另一方面也许有些读者可能在手机上观看,并不一定能很好的显示公式。但是如果非要有公式的话,我也会截图放到上面的。)。相关的数学推导会用PDF形式做好放在附录中。欢迎大家下载。不过如果想自己先推导的话,我当然是比较赞赏这种做法的啦!
注2:我自己的理解和感悟都用蓝色表示。正规的叙述用黑色表示。这样如果大家不想看我自己的评论的话,可以只看黑色的部分即可。
第一部分:课程概要
本课程中的老师、助教、如何考试、如何完成作业、project怎么做(BALABALA.......)。没有什么好记录的,因此舍去。
在这里给出老师建议的参考书:
1.阎守胜,固体物理基础,北京大学出版社(2011)
2.冯端、金国钧,凝聚态物理学,高等教育出版社(2013)
3.NRC,90年代物理学---凝聚态物理学,科学出版社(1992)
4.张礼, 近代物理学进展, 清华大学出版社(2009)
5.P.W.Anderson, Basic notions of condensed matter physics, Benjamin/Cummings,Menlo Park (1984)
6.P.M.Chaikin & T.C. Lubensky, Principles of condensed matter physics, Cambridge (1995).
7.Gerald D.Mahan, Condensed Matter in a Nutshell, Princeton (2011)
8.李正中,固体理论,高等教育出版社(2002)
第二部分:范式的建立与固体物理的范式
在科学的发展之中,范式的概念在起着很重要的作用。这一部分也许应该算在科学史当中,但是它对于下面行文的思路会有很大的帮助。因此把它放在这里也未尝不可。范式的概念是Thomas Kuhn在Harvard读理论物理博士的时候所提出的概念,记录在《The Structure of Scientific Revolutions》这本书当中。那么什么是范式呢?范式通俗来讲就是一个学科的结构,一个学科的灵魂性的概念和架构。那么科学在发展的时候避免不了6种情况:前范式阶段、常规科学阶段、反常阶段、危机阶段、科学革命阶段、新范式阶段。理解起来也很容易:当一个学科处于混沌状态的时候,只有只言片语的实验数据和理论,这时为前范式阶段;而当理论发展、实验数据越来越多的时候,有人就开始将理论搭建成一个框架(当然还不完善),并依据这个框架开始进行实验的指导以及理论的进步,这时称为常规科学阶段;当更多的实验现象被发现后,往往可能有一些现象与框架所预计的不相符合,这时可能能用一些策略解释,并没有对框架的根基产生什么影响,因此这时称为反常阶段;而当有决定性的实验事实被发现的时候(例如迈克尔逊莫雷实验),理论框架的根基产生了动摇,这时人们就要寻找新的范式或者在原有框架上进行修修补补,这样就进入了危机阶段;会有很大多数的人在这个时候参与到修修补补的工作当中来,他们中的几个人发现了新的范式或者是给出新的思路的时候,那么科学革命阶段将要开始;当新的范式被建立起来以后,人们又将进入下一个范式转换的轮回当中。科学就在这无穷无尽的范式转换中得到长足的发展。
我们以固体物理为例(毕竟它是我们高等固体物理的基础):固体物理的范式可以写成下面的样子:
“周期结构中波的传播规律”(1946年Brillouin的著作中有提到)。在这个范式中,我们可以看到两个概念:周期结构以及波。那么周期结构有哪些呢?一维(线性)、二维(平面)和三维(空间)周期结构。关于波我们将它分成三类:标量波(例如电子运动的波函数)、矢量波(电磁波)、张量波(晶格波)。下面就针对这些不同周期结构以及不同种类波进行讨论。Here we go!
Case 1:标量波(电子波函数)
在研究标量波的时候,我们以电子波函数为例。以多原子体系为例,每个原子核都会对电子有吸引作用,而电子之间会有排斥作用。在这个时候如果求解整个体系的准确Hamiltonian将会非常的困难(Hamiltonian写出来将会非常的长,而且其中会有很多的相互作用)。为了解决这个问题,Born和Oppenheimer提出了著名的B-O近似:将电子运动和核运动分离。核运动可看做经典力学,电子可看成外电场。而电子的运动则可以看做是在核所形成的势场当中所得到的薛定谔方程。这将系统的求解大大的简化了。但是依旧我们要处理的是多电子波函数。而这个是不好deal with的。因此我们下面又会用到单电子近似,也就是将单独的电子拿出来,针对它来说的话核对它的作用可看成势场;同样周围其他电子对它的作用也可以看成另外的势场(与核的吸引相反的排斥势能),这样我们就可以将多电子波函数转化成单电子波函数,得到了“单电子近似”。这时可以得到每个电子所处的能级的能量。然而当我们将很多的电子能级结合在一起的时候,它们就会形成一个带状结构,我们称它为“固体能带”。关于固体的性质很大程度上依赖于固体内部的能带结构。因此如何计算固体的能带结构,是固体物理课程的首要重点。(Question:电子波函数能求出来物质的何种性质?)
Case 2:矢量波(电磁波)
电磁波在固体中的运动可以得到物质的电磁性质或者光学性质。一个很重要的应用就是X衍射动力学。另外一个比较有趣的物质是光子晶体。既然电磁波可以在物质中传播,而光又是一种电磁波,那么能调节光在物质中的传播,那该多好。在1987年E.Yablonovitch在论文(PRL58,2059)中第一次提出了光子晶体的概念。在1990年的另外一篇文章(PRL65,3152)中从理论上预言了第一个有完整光子带隙的三维光子晶体。在1991年第一次在实验室用实验方法制备了有完整光子带隙的三维光子晶体,从而打开了光子晶体研究的大门。现代的光子晶体大多是人工设计、制备的。然而大自然中也有很多的光子晶体:蛋白石与蝴蝶翅膀。电磁波在周期型结构中所遵循的规律仍旧是Maxwell方程组,唯一不同的是加上了Bloch波的概念(周期波)。当一个光子晶体有了带隙以后,那么处在这个带隙频率中的光就无法通过光子晶体。它和半导体有很多的相似之处,下表就说明了它们之间的对比:
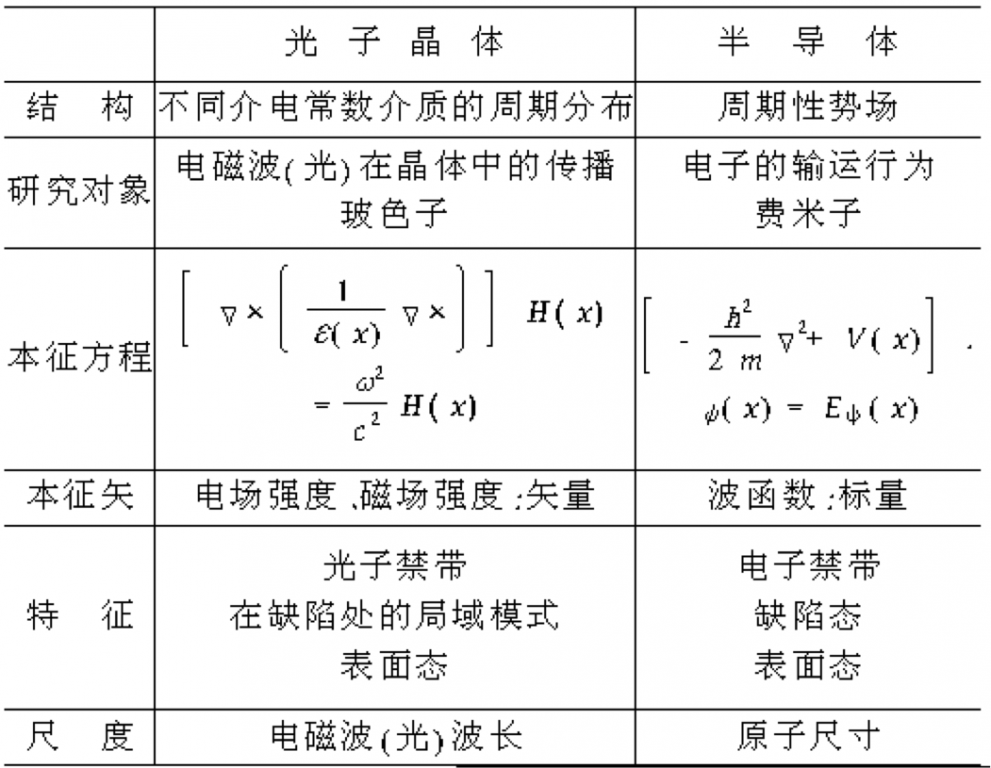
光子晶体有着很广泛的应用。例如做光子晶体光纤。我们知道,一般的光纤有如下的缺点:(1)有损耗和色散(2)单模光纤的直径较小(3)单模波长是有限的(4)特定的工作波长才可以使用。而光子晶体在这些方面都有着很大的优势:(1)无损耗、而且色散可根据光子晶体的结构来进行调制(2)已经可以制造大半径的光子晶体光纤(3)在光禁带范围内所有的波长都能进行单模工作。(Questions:(1)为什么单模光纤的直径比较小?(2)如何根据结构来调制色散?具体应该如何做?(3)何为单模工作?)另外可以运用到光子晶体的地方是改变原子的自发辐射速率。因为自发辐射速率是正比于光子态密度的。因此通过光子晶体改变光子的密度就可以改变自发辐射的速率。当处于光子晶体的原子的辐射频率落在完全光子能隙(Question: Explain this)中自发辐射被抑制,而落在不完全能隙中时自发辐射的速率被改变。对于完整的光子晶体来说,它的能隙是连续的。而对于其中有缺陷的(例如点缺陷(光子晶体微腔)和线缺陷(光子晶体波导))来说,会有一个缺陷模的存在,这个缺陷模的存在导致在能隙中的某些波长的光会透过光子晶体。
在普通光纤中,信息的传输如果想要转弯是需要很高成本的,因为普通光纤是运用全反射来进行传输的,而当出现偏转的时候就信息就会有遗失,这样要使得信息完整性得到保证的话,所用的光纤长度将会非常的长,成本会很高。但是光子晶体中可以使用一些缺陷位或者是线缺陷来调制光的行走路线。目前已经有实验进行了验证,效果比较好(PRL1996,77,3787 & Science1998,282:274)。并且也可以调制光子晶体去做门电路:进来频率的光为f1,f2,f3经过光子晶体之后只剩下了f1,f2。f3被吸收掉了。我们可以用这种性质来做“门电路”,因此可以进行逻辑运算,进而做出来光子晶体为主的计算机。当然要准确的计算出来光在光子晶体中的运动的话,需要求解带边界条件的Maxwell方程组,比较成熟的方法是使用时域有限差分方法。光子晶体还可以用来做信息的处理元件。将同一线路的信号进行分流。总而言之它的用处非常的大。
当然,这么好的性质是要付出代价的。上帝对所有人和物都是公平的。光子晶体所存在的问题有:
(1)制备Band Gap在可见光波长范围内的光子晶体还比较困难
(2)在任意位置上引入所需要的缺陷目前的技术还无法达到。(理论上的预期也不会太容易吧?)
(3)解决高效率光子传导材料的技术问题
(4)如何将现在的电流、电压加在光子晶体上的问题:因为我们要做器件的话,还是希望它用电比较的好。当然可以引入光电转换器来进行,不过具体的问题我也不是太清楚。得专门做器件的人才能知道。
在这里也可以谈谈科学与技术的问题。任何技术的发展都离不开基础研究,但是如何正确的对待科学和技术的区别,也是很重要的。在科学上我们只在乎Why和If的问题(为什么会这样?如果那样的话会怎样)而在对于技术的时候,我们需要考虑的就是How和What的问题(要做成什么样?怎么做?有什么用途)。两者的着眼点很有差别,在这里我想提一下。
Case 3:张量波(晶格波)
在这里我们讨论的是晶格的振动。晶格振动影响着固体的热学性质(比热、热导率等等)。最常见的模型就是一维原子链模型,具体的模型计算将会在附录中给出。当我们计算以后会发现有两种性质的色散关系。一种在原点左右的变化状态为线性的,而另外一种的斜率几乎为0。我们称线性部分为“声学支”,而斜率为0的部分为“光学支”。对于一个3维晶格来说,如果有N个原子,那么总的自由度为3N。在这3N个自由度中,能形成声学支的只有3个方向的(x,y,z),因为只有3个声学支。而剩下的3N-3个自由度都是光学支。
在我们讨论完三种case的波在周期性结构中的运动之后。下面我们就要谈论一下如何从固体物理推广到凝聚态物理当中。在固体物理中我们选择的是周期性结构。而在凝聚态物理中我们往往需要考察的体系都是局部无序或者整体无序的(在无序这章中有涉及)。而且研究内容从固体扩展到了非晶、液晶、准晶和液体当中。在性质的研究中也从原来的表观物理性质开始探究量子的相干性(相互作用体系)(例如输运性质)。在以后的课程中还会讲到凝聚态物理的范式:对称性破缺。对称性是一个系统十分重要的整体性质。
第三部分:量子化学的范式
化学从古到今都被人说成是“瓶瓶罐罐+摇摇晃晃”。但是当Kohn和Hohenberg提出来了密度泛函理论之后,化学将从原来的纯实验科学向理论与实验密切结合的科学发展。分子和原子属于量子力学所研究的范畴。而且一般的化学体系都是多粒子体系,因此从理论化学的发展可以看出多粒子体系应该如何处理。下面从价键理论到分子轨道理论分别介绍。
价键理论可以说是最基础也是最有效的化学理论。利用量子力学的观点来看,当一个体系写出了Hamiltonian的时候,下面的事情就是求解本征方程。目前来说价键理论最常用的就是使用变分法来进行求解(针对于H2来说)。变分波函数为电子在不同轨道上的排列。在有机化学当中会有杂化轨道这么一说。当然相信大家对于价键理论以及杂化轨道理论这种东西在高中或者大学化学中都学过了。因此在这里不再赘述。
分子轨道理论的基本思想是:电子在整个分子上有分布,这时的波函数为多电子波函数。而分子轨道是原来原子轨道的线性组合。能有效行程分子轨道的条件:(1)能量相近(2)对称性匹配(3)最大重叠。
第一节课和第二节课的笔记就记录在这里。未完待续,以后还会有更多更精彩的内容奉献给大家。欢迎持续关注。
附录一:一维原子链中晶格振动模型的求解
附录二:用变分法处理H2体系,得到正确的解
繞射原理
當光通過一單狹縫時,如縫愈窄則光線會愈向兩旁擴張,此現象即所謂的繞射。如圖
1(A)為光通過一孔洞(孔徑大小遠大於光波長時),在螢幕上呈現出孔的光點(圖中水
平軸顯示出光強度大小),圖1(B)當隨著孔徑變小時,光的繞射現象便明顯呈現在螢幕
上。
A.單狹縫的繞射實驗
實驗目的
觀察光通過單狹縫時所產生的繞射現象,並測量亮、暗紋的位置和理論值相比較。
實驗方法
將雷射光射入單狹縫片,即可在狹縫另一側之螢幕看見繞射圖案。假設令狹縫的寬度
為b,中心點為O 點,狹縫口被均分成若干點,如圖2 所示。
P0 點光程差為零,稱為中央亮區。P1 點至狹縫頂點的距離比到狹縫底點的距離大一波
長λ,亦就是說P1 點到狹縫頂點的距離,比P1 點到O 點的距離大半波長(λ/2),所以狹縫
頂點發出光波與由O 點發出的光波在P1 點的光程差為λ/2,干涉結果強度為零。同理狹縫
頂點以下第一點和O 點以下第一點的光程差也為半波長,故在P1 點其強度亦為零。如此,
兩兩相對,整個狹縫的二次子波在P1 點皆干涉為零,因此P1 點為一暗點。依此類推,P3
圖1(A) 圖1(B)
序决定激发,所以传播子既可以看成对序的描述也可以看成对激发的描述,这两种观点仅仅是视角的不同。狭义地说,人们倾向于把传播子的零频率分量称为序,而把有限频率分量称为激发。
零频率:gapless, energy gap
老杨曾经提出一个口号“对称性决定相互作用”,这句话可不可以用凝聚态 哈,早已被组长洗脑。 老杨曾经提出一个口号“对称性决定相互作用”,这句话可不可以用凝聚态的语言理解成“序决定激发”。
6 对称破缺和戈德斯通(Goldstone)定理
當光通過一單狹縫時,如縫愈窄則光線會愈向兩旁擴張,此現象即所謂的繞射。如圖
1(A)為光通過一孔洞(孔徑大小遠大於光波長時),在螢幕上呈現出孔的光點(圖中水
平軸顯示出光強度大小),圖1(B)當隨著孔徑變小時,光的繞射現象便明顯呈現在螢幕
上。
A.單狹縫的繞射實驗
實驗目的
觀察光通過單狹縫時所產生的繞射現象,並測量亮、暗紋的位置和理論值相比較。
實驗方法
將雷射光射入單狹縫片,即可在狹縫另一側之螢幕看見繞射圖案。假設令狹縫的寬度
為b,中心點為O 點,狹縫口被均分成若干點,如圖2 所示。
P0 點光程差為零,稱為中央亮區。P1 點至狹縫頂點的距離比到狹縫底點的距離大一波
長λ,亦就是說P1 點到狹縫頂點的距離,比P1 點到O 點的距離大半波長(λ/2),所以狹縫
頂點發出光波與由O 點發出的光波在P1 點的光程差為λ/2,干涉結果強度為零。同理狹縫
頂點以下第一點和O 點以下第一點的光程差也為半波長,故在P1 點其強度亦為零。如此,
兩兩相對,整個狹縫的二次子波在P1 點皆干涉為零,因此P1 點為一暗點。依此類推,P3
圖1(A) 圖1(B)
序决定激发,所以传播子既可以看成对序的描述也可以看成对激发的描述,这两种观点仅仅是视角的不同。狭义地说,人们倾向于把传播子的零频率分量称为序,而把有限频率分量称为激发。
零频率:gapless, energy gap
老杨曾经提出一个口号“对称性决定相互作用”,这句话可不可以用凝聚态 哈,早已被组长洗脑。 老杨曾经提出一个口号“对称性决定相互作用”,这句话可不可以用凝聚态的语言理解成“序决定激发”。
6 对称破缺和戈德斯通(Goldstone)定理
热力学中还存在一些状态参量,如体积、磁矩、电矩和摩尔数等,它们又是如何从对称性分析中产生出来的?回答是它们存在的基础是对称破缺和戈德斯通定理.譬如体积这个几何状态参量,它与对称破缺概念的联系,可通过晶体的形成过程加以说明.以固态的二氧化碳干冰)晶体为例,在・无限大・的气态O2中,随温度下降而在某局域形成晶核的过程,从对称性观点看,是系统从一个具有连续的完全对称性的气态转变为一个只有离散的较低对称性的固态的过程.在这类晶核化过程中,系统对称性突然自发地降低,称为系统的对称性的・破缺・.从固体物理学我们知道,晶体的振动模式可用波数k=2π/λ和圆频率ω(k)加以描述.长波模式变为简单的声波,并有线性关系ω=vk,故极端模式是在空间均匀的模式,振动频率趋向于零.此时半波长内就包含很多原胞,它们整体地沿同一方向运动,因此晶体可以近似地看成连续介质,而且具有确定的体积著名的物理学家P.W.安德森(Anderson)把这种对称破缺系统具有一个激发谱,当波长趋向无穷时,频率趋向零的性质概括为戈德斯通定理[4]. 相类似地在一些电极化材料例如HCl晶体中,位于格点上的HCl分子中,氢离子围绕相对大的氯离子转动,形成电偶极矩.在转变温度以上,这些电矩的取向是无序的;转变温度以下,偶极矩取向趋向有序,整个晶体拥有净电矩.晶体
从具有较高对称性的状态自发地降低对称性,转变为电矩具有确定轴取向的较低对称性的状态根据戈德斯通定理,这种对称破缺必将导致一个波长为无穷时零频率的元激发在极化晶体中,这类元激发由在净电矩指向附近轴的微小摆动形成的振荡波组成.类似的情况,在居里点附近的铁磁材料中也发生,从而在磁介质热力学中可以引进状态参量总的磁矩.
"Everett (╮(╯▽╰)╭ ~(= ̄ U  ̄=)~) 2014-04-22 12:30:48
1. 呃,我的意思应该是可以测量的是基态的响应而不是基态本身,而基态的响应依靠激发来实现,如果一个基态上没有激发,你将几乎无法测量这个基态。我们之所以可以通过磁化来测量铁磁基态的原因是铁磁基态上有很多低能的激发。没有激发的基态是没有响应的,就像理想真空一样。
2. 因为Goldstone mode的定义就是恢复对称性的长波涨落,Goldstone定理只不过进一步指出对于连续对称破缺,这些恢复对称性的模式是没有能隙的。SDW 的Goldstone mode是磁子,CDW的Goldstone mode是声子。磁子恢复磁性对称性,声子恢复平移对称性。
3. 因为spin wave是激发不是基态。同样是有空间指向性,放在基态上就是对称破缺,而放在激发上就是对称恢复。任何单个的磁子都没有SU(2)对称性,真是因为如此,把许多磁子乱糟糟地堆在一起,就会获得具有各种指向的自旋构型,磁子激发就像噪声一样打乱了基态的磁有序背景,从而起到恢复SU(2)对称性的作用。
"
什么是Majorana Fermion?
"Everett (╮(╯▽╰)╭ ~(= ̄ U  ̄=)~) 2014-04-22 12:30:48
1. 呃,我的意思应该是可以测量的是基态的响应而不是基态本身,而基态的响应依靠激发来实现,如果一个基态上没有激发,你将几乎无法测量这个基态。我们之所以可以通过磁化来测量铁磁基态的原因是铁磁基态上有很多低能的激发。没有激发的基态是没有响应的,就像理想真空一样。
2. 因为Goldstone mode的定义就是恢复对称性的长波涨落,Goldstone定理只不过进一步指出对于连续对称破缺,这些恢复对称性的模式是没有能隙的。SDW 的Goldstone mode是磁子,CDW的Goldstone mode是声子。磁子恢复磁性对称性,声子恢复平移对称性。
3. 因为spin wave是激发不是基态。同样是有空间指向性,放在基态上就是对称破缺,而放在激发上就是对称恢复。任何单个的磁子都没有SU(2)对称性,真是因为如此,把许多磁子乱糟糟地堆在一起,就会获得具有各种指向的自旋构型,磁子激发就像噪声一样打乱了基态的磁有序背景,从而起到恢复SU(2)对称性的作用。
"
什么是Majorana Fermion?
|
如何实现Majorana Fermion是现在凝聚态、原子光学等领域最火的一个方向。2011年APS March meeting有好几个会场都是和Majorana Fermion有关,当时很多人提出了各种模型号称可以观察到Majorana Fermion,在2012年APS March meeting就有好几个组报道了Majorana存在的证据。当然在我看来,有些结果可能是打酱油的。在这个领域里面, 有很多中国人在做,比如Fu Liang@Harvard, Yi Cui@Standford等等,其中Fu Liang的贡献最大。在国内Qi Kun Xue@Tsinghua做实验做得很好。我很佩服,因为Xue老师能够以最快的速度把握最前沿的研究方向。其实,国内的大学里面很牛的人很多,但是大部分都不能抓住前沿方向,自从回国以后就一直停留在自己以前做的方向,殊不知前沿的东西总是在变化,于是越做越艰难,越做越不能发好文章。当然这些是题外话,有感而发。这个领域进展神速,我差点就掉队了,不过幸好今年也做了几个个关于Majorana Fermion的理论工作,其中两个是半导体纳米线的,一个是冷原子的。不过每天浏览arxiv,基本上都可以看到关于Majorana的文章,有时候今天有了一个想法,明天就看到别人的文章贴出来了,想想,还是很惊心动魄的。
我们可以把任何一个Fermi子分解成实部和虚部
a = b + ic (Eq. 1)
其中, b, c为Majorana算子,而且满足 b+ = b, c+ = c, 这样我们可以证明{a, a+} = 1。 由于b, c也是Fermion,所以它们也满足{b, b+} =1, => b2 = 1/2, 类似的,{c, c+} =1, => c2 = 1/2。 其中1/2表示半个Fermion (half fermion),不是一个完整的Fermion。这个想法很不得了,写出这个公式来,也就注定流芳百世。
Eq. 1的反解可以得到
b = a + a+, c = i (a - a+)
我们可以定义a = h+, 也就是说,利用电子-空穴关系,这样我们有
b = a + h, c = i(a - h)
这个结果表明,每个Majorana粒子包括了等权重的电子(particle)-空穴(hole). 所以总的电荷等于0.这也是为什么Majorana
Fermion最早用于描述中微子的原因。由于总的电荷等于0,所以它不应该耦合电磁场。
物理和数学的差别也就在此,对于做数学的人来说,Eq. 1也许意味这某种变换,但是对于做物理的人而言,Eq.1应该有具体的物理意义,或者说,b, c应该不是虚拟的,而是有可能存在的。这一找,到现在找了80年,还是没有找到。最近几年之所以特别火,是因为也许我们终于可以找到了。想想,Majorana已经去世80年了,但是大家还是不能忘记他的思想,而且从来不记。
这里我要讨论一下proximity effect. 这个效应最早是用于研究磁学性质的,后来用于研究超导的proximity effect. 当把一个超导体和半导体放在一起,超导的库珀对会隧穿到半导体中,其空间范围和相干长度差不对。一般来说相干长度为um量级,但是半导体纳米线或者纳米阱一般为20 nm左右,所以proximity effect可以被观察到。由于超导体和半导体的接触一般都非常复杂,至于其proximity effect到底如何,其实是很难简单说明白的。现在大部分人都还没有开始关注这个问题,以后肯定会有很多。我们注意到自从Andreev reflection提出来以后,现在有大量的人关注界面对Andreev reflection的影响,也有很多tight-binding的文章。随着实验的进展,在超导的proximity effect上也肯定有很多。我已经写了一个tight-binding的程序,以后可以做这个方面的计算。这个方法最好的地方是可以研究disorder对proximity effect的影响。
http://blog.sciencenet.cn/blog-709494-558639.html 此文来自科学网龚明博客,转载请注明出处。
下一篇:行业自律是否可以杜绝腐败? 一个数学模型的理解
我们可以把任何一个Fermi子分解成实部和虚部
a = b + ic (Eq. 1)
其中, b, c为Majorana算子,而且满足 b+ = b, c+ = c, 这样我们可以证明{a, a+} = 1。 由于b, c也是Fermion,所以它们也满足{b, b+} =1, => b2 = 1/2, 类似的,{c, c+} =1, => c2 = 1/2。 其中1/2表示半个Fermion (half fermion),不是一个完整的Fermion。这个想法很不得了,写出这个公式来,也就注定流芳百世。
Eq. 1的反解可以得到
b = a + a+, c = i (a - a+)
我们可以定义a = h+, 也就是说,利用电子-空穴关系,这样我们有
b = a + h, c = i(a - h)
这个结果表明,每个Majorana粒子包括了等权重的电子(particle)-空穴(hole). 所以总的电荷等于0.这也是为什么Majorana
Fermion最早用于描述中微子的原因。由于总的电荷等于0,所以它不应该耦合电磁场。
物理和数学的差别也就在此,对于做数学的人来说,Eq. 1也许意味这某种变换,但是对于做物理的人而言,Eq.1应该有具体的物理意义,或者说,b, c应该不是虚拟的,而是有可能存在的。这一找,到现在找了80年,还是没有找到。最近几年之所以特别火,是因为也许我们终于可以找到了。想想,Majorana已经去世80年了,但是大家还是不能忘记他的思想,而且从来不记。
这种half fermion在现实世界中很难找到,尤其是在固体物理框架下很难观察到(很抱歉我对粒子物理不是很熟悉,但是我估计固体物理中也很难,因为尽管Majorana提出它的模型是为了揭示中微子,但是好像失败了)。其原因大概有这几个。(1) 固体物理基本都是和电荷有关,而且是电荷守恒的(U(1) gauge invariant,所以耦合电磁波); (2)按照公式(Eq.1)分解的两个half Fermion由于很强的库伦相互作用,所以很快会复合成单个普通的Fermion。(3)系统必须在某种拓扑区域。在实际过程中,要满足第二个条件,要求系统是金属,这样电荷的屏蔽效益可以让电子变成短程相互作用。第一个条件要求破坏U(1)规范不变性,比如超导体。 超导体基本可以同时满足第一和第二两个条件,但是很难满足第三个条件。因为绝大部分材料是s-wave的,p-wave的很少(实验证明还很难)。Green和Read在2000年的PRB证明p-wave超导体可以观察到这种粒子,这个工作很有启发性,也激发了很多人对超导体的兴趣(大量的工作都和这个工作有关,包括anomalous Andreev reflection等等). 但是由于这种超导体很少,要观察到这种粒子看似遥遥无期,我不指望。但是从物理上来说,研究p-wave的拓扑相变曾经是物理中的研究热点,包括其在冷原子物理中的一些实现,以及可能的拓扑量子计算 (S. Darma, Freedman等人做了很多工作,2006 - 2008年S. Darma组发了很多PRL文章都和它有关).
既然很难实现,那么是否有其它可能的方法?这个进展一个很有趣的想法是自旋轨道耦合+s-wave超导等价于一个p-wave超导体。它又激发了大家一轮新的讨论, 从2010年到现在,大量的工作都和这个想法有关。Chuanwei Zhang@WSU在2008年首先在冷原子中意识到了这个关系,后来在2010年被他的同事(Jay D. Sau et al) 应用到纳米线中(利用了proximity effect, Liang Fu在里面做了很多工作). 需要注意这个关系其实Rashba等人早就意识到了,它做了一个坐标变化于是得到了single pairing和triplet pairing, 但是他没有把它和拓扑相变以及Majorana联系在一起,于是和这么重要的发现失之交臂,可惜可惜。
这里我要讨论一下proximity effect. 这个效应最早是用于研究磁学性质的,后来用于研究超导的proximity effect. 当把一个超导体和半导体放在一起,超导的库珀对会隧穿到半导体中,其空间范围和相干长度差不对。一般来说相干长度为um量级,但是半导体纳米线或者纳米阱一般为20 nm左右,所以proximity effect可以被观察到。由于超导体和半导体的接触一般都非常复杂,至于其proximity effect到底如何,其实是很难简单说明白的。现在大部分人都还没有开始关注这个问题,以后肯定会有很多。我们注意到自从Andreev reflection提出来以后,现在有大量的人关注界面对Andreev reflection的影响,也有很多tight-binding的文章。随着实验的进展,在超导的proximity effect上也肯定有很多。我已经写了一个tight-binding的程序,以后可以做这个方面的计算。这个方法最好的地方是可以研究disorder对proximity effect的影响。
http://blog.sciencenet.cn/blog-709494-558639.html 此文来自科学网龚明博客,转载请注明出处。
下一篇:行业自律是否可以杜绝腐败? 一个数学模型的理解
1 yangwencao
发表评论 评论 (4 个评论)
- [3]霍东明
- 龚老师,我想问一下,什么是Majorana Fermion零模呢?
- 博主回复(2014-12-25 09:42):Majorana fermion has energy = 0, so it also called zero mode.
No comments:
Post a Comment