围绕生命起源，一个最困难也最有趣的谜题就是，存在于早期地球上的更简单分子如何形成这些遗传物质。从现代细胞中RNA的功能来看，RNA的出现似乎早于DNA。现代细胞合成蛋白质时，它们先把基因从DNA转录成RNA，然后以RNA为蓝图合成蛋白质。一开始，最后一步可能独立存在。后来，由于DNA化学稳定性极高，因而成为更加固定的信息存储载体。
研究者还有另一条理由认为RNA早于DNA出现。由RNA构成的酶被称为核酶（ribozyme），它在现代细胞中也发挥着关键作用。核糖体由RNA和蛋白质构成，功能是将RNA翻译成蛋白质。其中，催化蛋白质合成的主角正是RNA。因此，我们每一个细胞的核糖体都携带着来自原始RNA世界的“化石”证据——核酶。
目前许多研究的重点都是寻找RNA的起源。DNA和RNA这两种遗传分子都是多聚体（由更小的分子成串组成），基本组成单位是核苷酸。核苷酸有三种组分：糖、磷酸和碱基。碱基共有4种，它们就是核酸用于编码遗传信息的“字母”。在DNA中，这些“字母”是A、G、C和T，分别代表腺嘌呤、鸟嘌呤、胞嘧啶和胸腺嘧啶，而在RNA中，除了“字母”U（尿嘧啶）取代了T（见右图），其余“字母”都相同。碱基为富氮化合物，它们按照简单的原则而相互结合：如A与U（或T）配对，G与C配对。这样的配对构成了螺旋状DNA “梯子”（即双螺旋）的台阶，而且它们之间的特异性配对，对于如实复制遗传信息非常关键，因为只有这样细胞才能复制。与此同时，磷酸根和糖分子组成DNA或RNA链的“骨架”。
经过一系列步骤，氰化物、乙炔和水可以自我组装成碱基——这些简单分子存在于地球早期的原始物质中。简单的起始物质也易于聚集成糖。100多年前，研究者就已经知道，在碱性溶液中加热甲醛就可以得到多种糖分子混合物，而在早期行星上，是可以找到甲醛的。问题是如何得到合适的糖（如RNA的核糖）来制造核苷酸。两种发生在简单的二碳糖和三碳糖间的分子间反应，可以形成核糖及其他三种与核糖关系相近的糖分子。核糖这种形成方式并不能告诉我们，它为何能广泛存在于早期地球上，因为科学家已经证明核糖不稳定，即使在浓度很低的碱溶液中也会快速降解。过去，核糖的不稳定特性让很多研究者认为，第一个遗传分子可能不含核糖。但是本文作者里卡多和其他研究者发现了能使核糖稳定的方法。
核苷酸的磷酸根是另一个谜团。磷酸基团中的主要成分磷广泛存在于地壳中，但大部分存在于不易溶于水的矿物质中，而生命是从水中起源的。那么，磷酸根如何进入导致生命诞生的“原始汤”？科学家还不清楚。火山口处的高温可以将含磷酸盐的矿物转变成可溶性磷酸盐，但至少在现代火山中，释放出的磷数量很少。磷化合物的另一个潜在来源是磷铁镍陨石，在特定陨石上可以找到这种矿物质。
2005年，美国亚利桑那大学的马修·帕塞克（Matthew Pasek）和丹蒂·劳蕾塔（Dante Lauretta）发现，磷铁镍陨石（schreibersite）在水中的部分受到腐蚀后会释放出磷。这种途径看起来很有可能，因为陨石释放出来的磷比磷酸盐更易溶于水，也更易与有机化合物发生反应。
我们已知道至少一种可能得到碱基、糖和磷酸根的途径后，下一步就是将这三者合理地组装起来。但在过去几十年，这一步正是阻挡科学家前进的最大障碍。简单地将这三种成分混合于水中，它们并不会自发形成核苷酸——主要是因为每个连接反应都会涉及水分子的释放，而这种反应在水溶液中很难自发进行。要形成所需的化学键，就必须有能量供给，如在反应体系中加入富含能量的化合物。早期地球可能存在许多这样的化合物，然而在实验室中，这些分子只能启动低效的化学反应，在大多数情况下甚至完全不能启动反应。
今年春天，生命起源研究领域传出了令人振奋的消息。英国曼彻斯特大学的约翰·萨瑟兰（John Sutherland）和同事宣布，他们找到了一个似乎更可信的核苷酸形成途径，还回避了核糖不稳定的问题。萨瑟兰放弃了传统做法，不用碱基、糖和磷酸盐来制造核苷酸。他们的方法同样依赖于以前使用过的简单起始物质，如氰化物，乙炔和甲醛的衍生物。但与首先分别形成碱基和核糖，再将两者连接的做法相反，课题组将起始物质与磷酸盐混合。复杂的反应网络产生了一种名为2-氨基恶唑（2-aminooxazole）的小分子，可以把它看作糖分子的一个片段与碱基的一部分连在一起（见左图）的产物。在此途径的几个步骤中，磷酸盐起重要的催化作用。
2-氨基恶唑很稳定，它有一个重要特点：极易挥发。早期地球上，可能少量的2-氨基恶唑与其他化学物质一起形成在一个水池里，一旦水蒸发，2-氨基恶唑也随之挥发，在别处凝结为更纯净的2-氨基恶唑，成为一个原料库，为以后的化学反应做好准备：形成完整的糖和碱基，并连接在一起。
萨瑟兰的方法还有一个好处是，某些前期反应的副产品有利于后期反应的进行。不过，这种方法除了产生“正确”的核苷酸外，还会生成“不正确”的核苷酸：某些情况下，糖和碱基不能正确连接。令人惊讶的是，在紫外光下——强烈的太阳紫外光照射在早期地表浅层水域——会破坏“不正确”的核苷酸，留下“正确的”核苷酸。最终结果是一条异常清晰的C和U的组装路线图。当然，我们还需要得到G和A的组装路线图，因此挑战仍然存在。但在解释RNA如何在早期地球形成的问题上，萨瑟兰小组的工作迈出了一大步。
在总结第一次和第二次上课的笔记之前，让我们思考一个问题：什么是物理学？当然这个问题问不同的人会有不同的答案，那么在这里我给出我自己的答案，供大家参考和拍砖。我认为的物理学是“考察自然界中物质的性质和演化的科学”。既然是物质，就一定会有组成和性质；既然是演化，就一定会有演化的规律。这两个问题基本涵盖了物理学中的绝大部分领域。也是我们下面整理的一个重点。
为什么我们要这么来做呢？毕竟高等固体物理这门课主要研究的是固体物理或者更广泛一点的凝聚态物理中物质的性质以及它们可能发生的演化方法。在物质性质中，我们比较常见的有：力学性质、热学性质、光学性质、电磁性质等等。而演化中往往是在一定条件下所进行的，因此我们要探究物质的演化规律。因此整个高等固体物理讲述的是这么一件事：“在凝聚态物理框架下探究物质的物理性质及系统演化规律的学科”。前面的废话先说到这里，下面让我们一起进入高等固体物理的课堂当中吧。
注1：因为下面所说的是笔记中的重新整理，可能叙述顺序可能与一般书本上的不太一样，当然这也带有了我个人的风格和理解在里面。我尽量把语言变得通俗一点，能不使用公式的地方尽量不适用ugly的大长串公式（一方面是为我个人方面，另一方面也许有些读者可能在手机上观看，并不一定能很好的显示公式。但是如果非要有公式的话，我也会截图放到上面的。）。相关的数学推导会用PDF形式做好放在附录中。欢迎大家下载。不过如果想自己先推导的话，我当然是比较赞赏这种做法的啦！
注2：我自己的理解和感悟都用蓝色表示。正规的叙述用黑色表示。这样如果大家不想看我自己的评论的话，可以只看黑色的部分即可。
第一部分：课程概要
本课程中的老师、助教、如何考试、如何完成作业、project怎么做（BALABALA.......）。没有什么好记录的，因此舍去。
在这里给出老师建议的参考书：
1.阎守胜，固体物理基础，北京大学出版社(2011)
2.冯端、金国钧，凝聚态物理学，高等教育出版社(2013)
3.NRC，90年代物理学---凝聚态物理学，科学出版社(1992)
4.张礼, 近代物理学进展, 清华大学出版社(2009)
5.P.W.Anderson, Basic notions of condensed matter physics, Benjamin/Cummings,Menlo Park (1984)
6.P.M.Chaikin & T.C. Lubensky, Principles of condensed matter physics, Cambridge (1995).
7.Gerald D.Mahan, Condensed Matter in a Nutshell, Princeton (2011)
8.李正中，固体理论，高等教育出版社(2002)
第二部分：范式的建立与固体物理的范式
在科学的发展之中，范式的概念在起着很重要的作用。这一部分也许应该算在科学史当中，但是它对于下面行文的思路会有很大的帮助。因此把它放在这里也未尝不可。范式的概念是Thomas Kuhn在Harvard读理论物理博士的时候所提出的概念，记录在《The Structure of Scientific Revolutions》这本书当中。那么什么是范式呢？范式通俗来讲就是一个学科的结构，一个学科的灵魂性的概念和架构。那么科学在发展的时候避免不了6种情况：前范式阶段、常规科学阶段、反常阶段、危机阶段、科学革命阶段、新范式阶段。理解起来也很容易：当一个学科处于混沌状态的时候，只有只言片语的实验数据和理论，这时为前范式阶段；而当理论发展、实验数据越来越多的时候，有人就开始将理论搭建成一个框架（当然还不完善），并依据这个框架开始进行实验的指导以及理论的进步，这时称为常规科学阶段；当更多的实验现象被发现后，往往可能有一些现象与框架所预计的不相符合，这时可能能用一些策略解释，并没有对框架的根基产生什么影响，因此这时称为反常阶段；而当有决定性的实验事实被发现的时候（例如迈克尔逊莫雷实验），理论框架的根基产生了动摇，这时人们就要寻找新的范式或者在原有框架上进行修修补补，这样就进入了危机阶段；会有很大多数的人在这个时候参与到修修补补的工作当中来，他们中的几个人发现了新的范式或者是给出新的思路的时候，那么科学革命阶段将要开始；当新的范式被建立起来以后，人们又将进入下一个范式转换的轮回当中。科学就在这无穷无尽的范式转换中得到长足的发展。
我们以固体物理为例（毕竟它是我们高等固体物理的基础）：固体物理的范式可以写成下面的样子：
“周期结构中波的传播规律”（1946年Brillouin的著作中有提到）。在这个范式中，我们可以看到两个概念：周期结构以及波。那么周期结构有哪些呢？一维（线性）、二维（平面）和三维（空间）周期结构。关于波我们将它分成三类：标量波（例如电子运动的波函数）、矢量波（电磁波）、张量波（晶格波）。下面就针对这些不同周期结构以及不同种类波进行讨论。Here we go!
Case 1：标量波（电子波函数）
在研究标量波的时候，我们以电子波函数为例。以多原子体系为例，每个原子核都会对电子有吸引作用，而电子之间会有排斥作用。在这个时候如果求解整个体系的准确Hamiltonian将会非常的困难（Hamiltonian写出来将会非常的长，而且其中会有很多的相互作用）。为了解决这个问题，Born和Oppenheimer提出了著名的B-O近似：将电子运动和核运动分离。核运动可看做经典力学，电子可看成外电场。而电子的运动则可以看做是在核所形成的势场当中所得到的薛定谔方程。这将系统的求解大大的简化了。但是依旧我们要处理的是多电子波函数。而这个是不好deal with的。因此我们下面又会用到单电子近似，也就是将单独的电子拿出来，针对它来说的话核对它的作用可看成势场；同样周围其他电子对它的作用也可以看成另外的势场（与核的吸引相反的排斥势能），这样我们就可以将多电子波函数转化成单电子波函数，得到了“单电子近似”。这时可以得到每个电子所处的能级的能量。然而当我们将很多的电子能级结合在一起的时候，它们就会形成一个带状结构，我们称它为“固体能带”。关于固体的性质很大程度上依赖于固体内部的能带结构。因此如何计算固体的能带结构，是固体物理课程的首要重点。（Question：电子波函数能求出来物质的何种性质？）
Case 2：矢量波（电磁波）
电磁波在固体中的运动可以得到物质的电磁性质或者光学性质。一个很重要的应用就是X衍射动力学。另外一个比较有趣的物质是光子晶体。既然电磁波可以在物质中传播，而光又是一种电磁波，那么能调节光在物质中的传播，那该多好。在1987年E.Yablonovitch在论文（PRL58，2059）中第一次提出了光子晶体的概念。在1990年的另外一篇文章（PRL65，3152）中从理论上预言了第一个有完整光子带隙的三维光子晶体。在1991年第一次在实验室用实验方法制备了有完整光子带隙的三维光子晶体，从而打开了光子晶体研究的大门。现代的光子晶体大多是人工设计、制备的。然而大自然中也有很多的光子晶体：蛋白石与蝴蝶翅膀。电磁波在周期型结构中所遵循的规律仍旧是Maxwell方程组，唯一不同的是加上了Bloch波的概念（周期波）。当一个光子晶体有了带隙以后，那么处在这个带隙频率中的光就无法通过光子晶体。它和半导体有很多的相似之处，下表就说明了它们之间的对比：
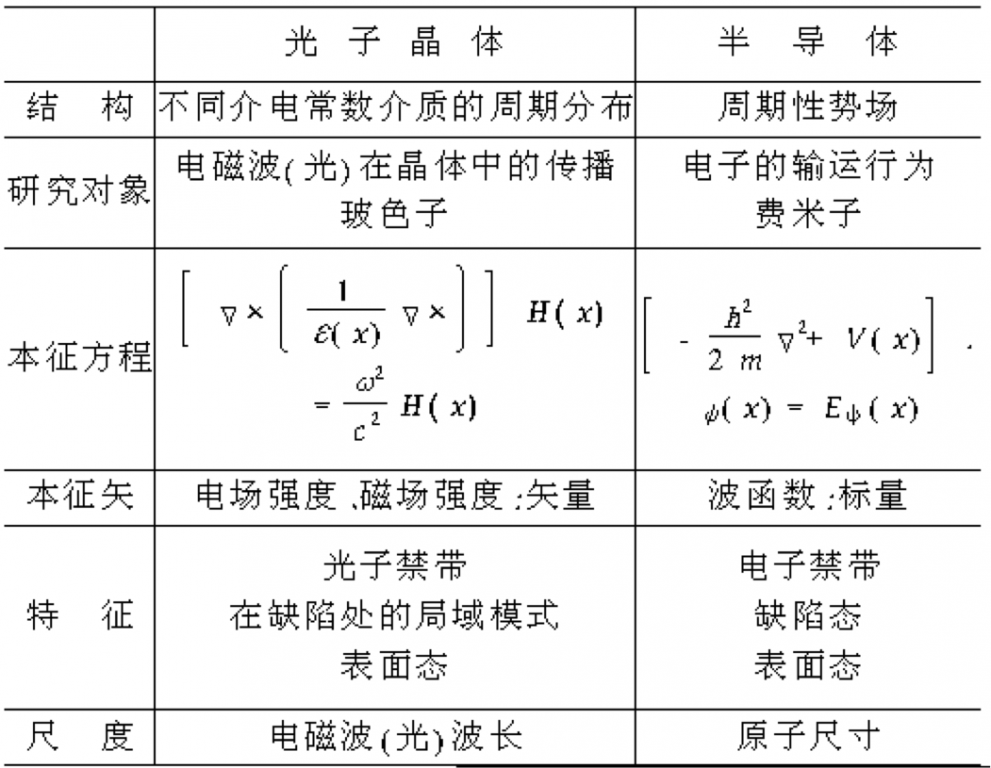
光子晶体有着很广泛的应用。例如做光子晶体光纤。我们知道，一般的光纤有如下的缺点：（1）有损耗和色散（2）单模光纤的直径较小（3）单模波长是有限的（4）特定的工作波长才可以使用。而光子晶体在这些方面都有着很大的优势：（1）无损耗、而且色散可根据光子晶体的结构来进行调制（2）已经可以制造大半径的光子晶体光纤（3）在光禁带范围内所有的波长都能进行单模工作。（Questions：（1）为什么单模光纤的直径比较小？（2）如何根据结构来调制色散？具体应该如何做？（3）何为单模工作？）另外可以运用到光子晶体的地方是改变原子的自发辐射速率。因为自发辐射速率是正比于光子态密度的。因此通过光子晶体改变光子的密度就可以改变自发辐射的速率。当处于光子晶体的原子的辐射频率落在完全光子能隙（Question: Explain this）中自发辐射被抑制，而落在不完全能隙中时自发辐射的速率被改变。对于完整的光子晶体来说，它的能隙是连续的。而对于其中有缺陷的（例如点缺陷（光子晶体微腔）和线缺陷（光子晶体波导））来说，会有一个缺陷模的存在，这个缺陷模的存在导致在能隙中的某些波长的光会透过光子晶体。
在普通光纤中，信息的传输如果想要转弯是需要很高成本的，因为普通光纤是运用全反射来进行传输的，而当出现偏转的时候就信息就会有遗失，这样要使得信息完整性得到保证的话，所用的光纤长度将会非常的长，成本会很高。但是光子晶体中可以使用一些缺陷位或者是线缺陷来调制光的行走路线。目前已经有实验进行了验证，效果比较好（PRL1996，77，3787 & Science1998，282：274）。并且也可以调制光子晶体去做门电路：进来频率的光为f1,f2,f3经过光子晶体之后只剩下了f1,f2。f3被吸收掉了。我们可以用这种性质来做“门电路”，因此可以进行逻辑运算，进而做出来光子晶体为主的计算机。当然要准确的计算出来光在光子晶体中的运动的话，需要求解带边界条件的Maxwell方程组，比较成熟的方法是使用时域有限差分方法。光子晶体还可以用来做信息的处理元件。将同一线路的信号进行分流。总而言之它的用处非常的大。
当然，这么好的性质是要付出代价的。上帝对所有人和物都是公平的。光子晶体所存在的问题有：
（1）制备Band Gap在可见光波长范围内的光子晶体还比较困难
（2）在任意位置上引入所需要的缺陷目前的技术还无法达到。（理论上的预期也不会太容易吧？）
（3）解决高效率光子传导材料的技术问题
（4）如何将现在的电流、电压加在光子晶体上的问题：因为我们要做器件的话，还是希望它用电比较的好。当然可以引入光电转换器来进行，不过具体的问题我也不是太清楚。得专门做器件的人才能知道。
在这里也可以谈谈科学与技术的问题。任何技术的发展都离不开基础研究，但是如何正确的对待科学和技术的区别，也是很重要的。在科学上我们只在乎Why和If的问题（为什么会这样？如果那样的话会怎样）而在对于技术的时候，我们需要考虑的就是How和What的问题（要做成什么样？怎么做？有什么用途）。两者的着眼点很有差别，在这里我想提一下。
Case 3：张量波（晶格波）
在这里我们讨论的是晶格的振动。晶格振动影响着固体的热学性质（比热、热导率等等）。最常见的模型就是一维原子链模型，具体的模型计算将会在附录中给出。当我们计算以后会发现有两种性质的色散关系。一种在原点左右的变化状态为线性的，而另外一种的斜率几乎为0。我们称线性部分为“声学支”，而斜率为0的部分为“光学支”。对于一个3维晶格来说，如果有N个原子，那么总的自由度为3N。在这3N个自由度中，能形成声学支的只有3个方向的（x,y,z），因为只有3个声学支。而剩下的3N-3个自由度都是光学支。
在我们讨论完三种case的波在周期性结构中的运动之后。下面我们就要谈论一下如何从固体物理推广到凝聚态物理当中。在固体物理中我们选择的是周期性结构。而在凝聚态物理中我们往往需要考察的体系都是局部无序或者整体无序的（在无序这章中有涉及）。而且研究内容从固体扩展到了非晶、液晶、准晶和液体当中。在性质的研究中也从原来的表观物理性质开始探究量子的相干性（相互作用体系）（例如输运性质）。在以后的课程中还会讲到凝聚态物理的范式：对称性破缺。对称性是一个系统十分重要的整体性质。
第三部分：量子化学的范式
化学从古到今都被人说成是“瓶瓶罐罐+摇摇晃晃”。但是当Kohn和Hohenberg提出来了密度泛函理论之后，化学将从原来的纯实验科学向理论与实验密切结合的科学发展。分子和原子属于量子力学所研究的范畴。而且一般的化学体系都是多粒子体系，因此从理论化学的发展可以看出多粒子体系应该如何处理。下面从价键理论到分子轨道理论分别介绍。
价键理论可以说是最基础也是最有效的化学理论。利用量子力学的观点来看，当一个体系写出了Hamiltonian的时候，下面的事情就是求解本征方程。目前来说价键理论最常用的就是使用变分法来进行求解（针对于H2来说）。变分波函数为电子在不同轨道上的排列。在有机化学当中会有杂化轨道这么一说。当然相信大家对于价键理论以及杂化轨道理论这种东西在高中或者大学化学中都学过了。因此在这里不再赘述。
分子轨道理论的基本思想是：电子在整个分子上有分布，这时的波函数为多电子波函数。而分子轨道是原来原子轨道的线性组合。能有效行程分子轨道的条件：（1）能量相近（2）对称性匹配（3）最大重叠。
第一节课和第二节课的笔记就记录在这里。未完待续，以后还会有更多更精彩的内容奉献给大家。欢迎持续关注。
附录一：一维原子链中晶格振动模型的求解
附录二：用变分法处理H2体系，得到正确的解
http://bridgetunnelinvestor.freeforums.net/thread/1254/therapy-editing-primer-tools-emerging#ixzz3ad6xQBRg
Our Quick Thoughts On Gene Editing
Targeted nucleases are powerful tools for mediating genome alteration with high
precision, and holds enormous potential for therapeutic applications to treat many
diseases for which no curative treatments are available.
Gene editing has come a long way and interest/optimism in genome engineering is
increasing, boosted by the recent discovery that the RNA-guided Ca9 nuclease from the
microbial clustered regularly interspaced short palindromic repeats (CRISPR) adaptive
immune system can be used to edit human cells.
With significant improvement in delivery and nuclease design, ZFNs, TALENs and CRISPRcas9
are capable of achieving high efficiency in human cells (up to 80%) which should be
sufficient to drive therapeutic benefit for many indications.
The most recent update on SGMO’s HIV program (at ASGCT 2015) shows 3-year safety
data for ZFN-mediated CCR5 knockout, indicating that gene editing is a safe, viable
therapeutic class.
其中 
其中 
其中 
，其中 
其中 
No comments:
Post a Comment