倒三角是一个算符,意思是分别对ψ(x,y,z)的x,y,z坐标求偏导的平方和, ▽2ψ(x,y,z)+(8π2m/h2)[E-U(x,y,z)]ψ(x,y,z)=0
http://quantway.lofter.com/post/42866f_179de26
如果我们利用某个关系函数,比如Y=F(X),代入一个X算出一个Y,又将Y作为新的X再次计算下一个Y………如此不断,这种方法在数学上称为迭代,
Clifford 几何代数的基本观点
||
高斯认为:曲面上的曲线微分长度平方、曲面上曲线的弯曲量度(曲率)是曲面上的任意曲线的基本度量量,具客观性。这是物理性的,为整个曲面几何理论的要素。这里,最小的几何单位是微元曲线、及两条正交微元曲线所形成的微元面。这个几何是没有点概念的。因为点是空(0长度,0面积)。
Clifford 几何代数的基本观点就是:物理上有意义的流形变换是保证上面的两类量的客观不变性。
高斯认为:曲面上的曲线微分长度平方、曲面上曲线的弯曲量度(曲率)是曲面上的任意曲线的基本度量量,具客观性。这是物理性的,为整个曲面几何理论的要素。这里,最小的几何单位是微元曲线、及两条正交微元曲线所形成的微元面。这个几何是没有点概念的。因为点是空(0长度,0面积)。
Clifford 几何代数的基本观点就是:物理上有意义的流形变换是保证上面的两类量的客观不变性。
音乐快递:"投影取值测度" - 由marketreflections发表- 文学城
bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁
2010年6月12日 - Von Neumann的那个年代,而是从传统“投影取值测度”(PV,又称“谱测度”)推广到“http://media.open.com.cn/media_file/rm/dongshi2005/liangzilixue/E_index5.htm
选定一个力学量
 表象时,就相当于选定这个希尔伯特空间的一个坐标系
表象时,就相当于选定这个希尔伯特空间的一个坐标系
§5。3 狄拉克符号
 。 (5.3.1)
。 (5.3.1)
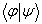 是一个复数。对于归一化的右矢,
是一个复数。对于归一化的右矢,  。设
。设 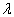 为任一复数,由上式得到
为任一复数,由上式得到
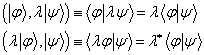 。 (5.3.2)
。 (5.3.2)
 , 当且仅当
, 当且仅当
 ,
, 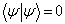 。 (5.3.3)
。 (5.3.3)
 (5.3.4)
(5.3.4)
§5.3.1 左矢(bra)和右矢(ket)
我们知道,矢量之间的内在关系,例如两个矢量的内积或叉乘,不是必须用坐标系才能表达。很多情况下,不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中,一个体系的任一个状态波函数  都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量  表象时,就相当于选定这个希尔伯特空间的一个坐标系。
表象时,就相当于选定这个希尔伯特空间的一个坐标系。  的本征矢
的本征矢  就是这个希尔伯特空间的基。态矢量在各个基上的分量
就是这个希尔伯特空间的基。态矢量在各个基上的分量  就组成了这个状态在
就组成了这个状态在  表象时的状态波函数(一个列矩阵)。态矢量在一个基
表象时的状态波函数(一个列矩阵)。态矢量在一个基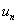 上的分量
上的分量  就是这个基相应的本征值
就是这个基相应的本征值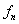 出现的概率幅,
出现的概率幅,  是
是  与
与 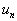 的内积
的内积 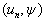 。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
 都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量  表象时,就相当于选定这个希尔伯特空间的一个坐标系。
表象时,就相当于选定这个希尔伯特空间的一个坐标系。  的本征矢
的本征矢  就是这个希尔伯特空间的基。态矢量在各个基上的分量
就是这个希尔伯特空间的基。态矢量在各个基上的分量  就组成了这个状态在
就组成了这个状态在  表象时的状态波函数(一个列矩阵)。态矢量在一个基
表象时的状态波函数(一个列矩阵)。态矢量在一个基 就是这个基相应的本征值
就是这个基相应的本征值 是
是  与
与 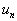 的内积
的内积 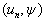 。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
实际上,在讨论表象理论时,一开始用狄拉克符号方法就能够很方便简洁地导出态矢量、算符的表象及表象的变换,而不是必须从坐标表象开始。前面从坐标表象开始,仅仅是为了理解方便。
狄拉克符号是将一个体系中的任一个态矢量  用相应的一个所谓右矢
用相应的一个所谓右矢  来表示。这里
来表示。这里  应理解为与具体表象有关的波函数,而写为
应理解为与具体表象有关的波函数,而写为  时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为
时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为  是一个与具体表象无关的抽象的态矢量,而
是一个与具体表象无关的抽象的态矢量,而  是与具体表象有关的态矢量,是
是与具体表象有关的态矢量,是  的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
 用相应的一个所谓右矢
用相应的一个所谓右矢  来表示。这里
来表示。这里  应理解为与具体表象有关的波函数,而写为
应理解为与具体表象有关的波函数,而写为  时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为
时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为  是一个与具体表象无关的抽象的态矢量,而
是一个与具体表象无关的抽象的态矢量,而  是与具体表象有关的态矢量,是
是与具体表象有关的态矢量,是  的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积, 。 (5.3.1)
。 (5.3.1)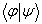 是一个复数。对于归一化的右矢,
是一个复数。对于归一化的右矢,  。设
。设 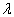 为任一复数,由上式得到
为任一复数,由上式得到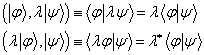 。 (5.3.2)
。 (5.3.2) , 当且仅当
, 当且仅当  ,
, 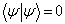 。 (5.3.3)
。 (5.3.3) (5.3.4)
(5.3.4)
式中, 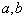 为任意常数; 若
为任意常数; 若 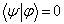 ,则称
,则称  与
与  两个态矢是相互正交的。
两个态矢是相互正交的。
[PDF]第四章矩阵力学基础(Ⅱ)——表象理论
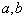 为任意常数; 若
为任意常数; 若 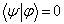 ,则称
,则称  与
与  两个态矢是相互正交的。
两个态矢是相互正交的。[PDF]第四章矩阵力学基础(Ⅱ)——表象理论
jpk.cust.edu.cn/lzlx/uploadimg/20075192111534.pdf
轉為繁體網頁
引言: 在上一章中我们讨论了力学量的算符表示以及算符的运动方程。通过 ... 在数学中,一个矢量,在选定坐标系后,可. 以用它在该坐标 ... 为表述态和算符,需要在希尔轉為繁體網頁
[FLASH]体系的任何一个状态体系的任何一个状态所描写的态中测量
web.zzuli.edu.cn/picture/.../8143fe17-4886-4338-9956-f4516100b6e2.swf
这正是本章要讨论的内容,这个空间就是希尔伯特空间。 ... 选定了Q 表象就相当于选量子力学中,表象变换问题,求助- 物理- 小木虫- 学术科研第一站
emuch.net/html/201308/6207603.html
轉為繁體網頁
轉為繁體網頁
2013年8月6日 - 20 篇文章 - 4 位作者
说简单一些,即是选定了表象,就选中了希尔伯特空间的一组基底,就是选择 ... 但是物理在不同表象中的数学形式不同,动量表象和坐标表象之间的变换是一个 ... 表示这个向量时,既可以采取直角坐标系,也可以采取极坐标系。 ... F表象中的波函数它们实际上是态矢量在力学量算符F的各个本征态矢量上的投影分量。[PPT]下载 - 欢迎来到重庆邮电大学理学院
slxy.cqupt.edu.cn/lzlx/admin/.../20101110163630581.ppt
轉為繁體網頁
前面所使用的波函数及力学量算符是以坐标这个力学量算符的本征值为变量写出它们的具体形式的。那么,是否 .... 在三维矢量空间选一组正交归一完备基 ... 选定轉為繁體網頁
[PDF]第三章量子力学中的力学量
wldz.ldxy.edu.cn/lzlx/dzja3.pdf
轉為繁體網頁
在选定了一定的“坐标系”或. 称表象后,算符 ... 状态时,它的力学量,如坐标、动量、轉為繁體網頁
量子力学表象及其互换_百度文库
wenku.baidu.com/view/9cc8e3f9fab069dc502201ac.html - 轉為繁體網頁
2011年10月8日 - 在数学中,一个矢量,在选定坐标系后,可以用它在该坐标系中的一组分量来表示 ... 学中, 在量子力学中,态和力学量的具体表达方式称为表象。 ... 描述同一个状态, 是这个状态在坐范围内测量粒子动量的几率。ψ ( x, ..... 基矢上的投影即矢在希尔伯特第1章 量子理论的实验基础 从17世纪到19世纪末
media.open.com.cn/media_file/rm/.../chapter5/5_6.htm
轉為繁體網頁
很多情况下,不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中, ... 在选定一个力学量 表象时,就相当于选定这个希尔伯特空间的一个坐标系。轉為繁體網頁
第四章矩阵力学基础(Ⅱ)——表象理论_0x94文档库
www.0x94.com/doc/0NWp2ug3OLXjs67Zx.html
轉為繁體網頁
引言: 在上一章中我们讨论了力学量的算符表示以及算符的运动方程。通过将正则 ... 在给定表象,即给定希尔伯特空间的一组基底后,算符用矩阵表示。 ... 在数学中,轉為繁體網頁
No comments:
Post a Comment