双曲动力系统(期中考试)
刚刚参加Marcelo
Viana教授的Hyperbolic Dynamics的博士课程的期中考试,一共四道题目。
题目一:设 为一个
为一个 的实值函数,期中
的实值函数,期中 .令
.令 .证明如果
.证明如果 是向量场
是向量场 的奇点,则
的奇点,则 的特征值都是实数。证明如果
的特征值都是实数。证明如果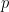 是一个双曲形的奇点当且仅当双线性形式
是一个双曲形的奇点当且仅当双线性形式 是非退化的。更进一步的,证明
是非退化的。更进一步的,证明 不包含周期轨道。
不包含周期轨道。
证明提纲:在欧式空间中,梯度场由于是由函数的的各方向导数所得来的,我们发现它的导数在局部坐标下看是一个对称阵,于是我们得出相应的特征值都应当是实数。而将坐标拉回也不影响这个结果。而沿着梯度场,函数 的值是严格递增的,不可能出现周期点。(反证法)
的值是严格递增的,不可能出现周期点。(反证法)
题目二:令 为一个微分同胚,令
为一个微分同胚,令 为
为 的双曲不变集合(Hyperbolic set).设
的双曲不变集合(Hyperbolic set).设 为两个周期点并定义
为两个周期点并定义
 在某点横截的与
在某点横截的与 相交
相交
再定义 .
.
证明上面定义的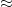 是一个等价关系.更进一步的,证明对任意的开集
是一个等价关系.更进一步的,证明对任意的开集 和
和 与同一个等价类相交非空,则存在
与同一个等价类相交非空,则存在 ,使得
,使得 .
.
证明提纲:验证等价类的定义,关键在于验证传递性。而这里我们需要证明的关键是,对于三个点 ,满足
,满足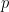 的不稳定流形和
的不稳定流形和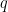 的稳定流形横截相交;
的稳定流形横截相交;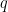 的不稳定流形和
的不稳定流形和 的稳定流形横截相交,可以推出
的稳定流形横截相交,可以推出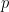 的不稳定流形与
的不稳定流形与 的稳定流形也是横截相交的。而这个证明需要
的稳定流形也是横截相交的。而这个证明需要 引理。
引理。
对于第二个问,对于这两个任意给定的开集合 和
和 ,我们在其中寻找到等价类的点,比如说
,我们在其中寻找到等价类的点,比如说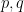 ,则我们可以分别作出
,则我们可以分别作出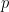 的不稳定流形和
的不稳定流形和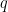 的稳定流形.注意,他们是横截相交的。设交点为
的稳定流形.注意,他们是横截相交的。设交点为 ,则我们可以利用稳定流形和不稳定流形的性质,得出存在
,则我们可以利用稳定流形和不稳定流形的性质,得出存在 .
.
题目三:令 .证明如果
.证明如果 是一个
是一个 微分同胚,并满足
微分同胚,并满足 与
与 可交换(就是说,
可交换(就是说, ),则
),则 是线性的。而另一方面,存在
是线性的。而另一方面,存在 上的
上的 的微分同胚,与
的微分同胚,与 可交换,却不是线性的变换。
可交换,却不是线性的变换。
证明提纲:由题目条件,我们得出 .于是,首先,我们可以得到
.于是,首先,我们可以得到 .于是,由于
.于是,由于 ,而
,而 ,我们有,
,我们有, .现在任取
.现在任取 ,我们有
,我们有 .于是
.于是 对所有
对所有 成立。
成立。
第二个问,我们构造函数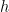 定义如下,
定义如下, .这是一个非线性的函数,满足与
.这是一个非线性的函数,满足与 可交换。
可交换。
题目四:令 为一个
为一个 类的微分同胚,其中
类的微分同胚,其中 是一个compact的流形。证明如果
是一个compact的流形。证明如果 是结构稳定的,则
是结构稳定的,则 的所有不动点都是双曲不动点。我们能对周期
的所有不动点都是双曲不动点。我们能对周期 的周期点有同样的断言吗?
的周期点有同样的断言吗?
证明提纲: 是结构稳定的,首要的事情就是它的不动点都是simple的。再加上流形是紧致的,于是我们可以证明不动点一定是有限个。假设我们有一个不动点
是结构稳定的,首要的事情就是它的不动点都是simple的。再加上流形是紧致的,于是我们可以证明不动点一定是有限个。假设我们有一个不动点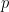 ,
, 在该点不是双曲的。这样,只需在局部分析这个不动点。把它先push到坐标上去,再将函数在那里通过一个bump函数微微调整,最后在pull
back这个函数,我们最终可以得到两个不同的函数,
在该点不是双曲的。这样,只需在局部分析这个不动点。把它先push到坐标上去,再将函数在那里通过一个bump函数微微调整,最后在pull
back这个函数,我们最终可以得到两个不同的函数, 他们在
他们在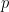 点都是双曲的,但是他们稳定流形和不稳定流形的维数不同。这样他们是不可能共轭的。(P.S.本题具体写起来最麻烦。)
点都是双曲的,但是他们稳定流形和不稳定流形的维数不同。这样他们是不可能共轭的。(P.S.本题具体写起来最麻烦。)
为了给出一个反例,我构造了圆周上的微分同胚,满足每个点都是周期为2的周期点。同时这个微分同胚共轭于圆周的旋转,从而是结构稳定的。但是我构造出来的例子中,该圆周有非双曲的周期点,即,导数正好为 .
.
题目一:设
证明提纲:在欧式空间中,梯度场由于是由函数的的各方向导数所得来的,我们发现它的导数在局部坐标下看是一个对称阵,于是我们得出相应的特征值都应当是实数。而将坐标拉回也不影响这个结果。而沿着梯度场,函数
题目二:令
再定义
证明上面定义的
证明提纲:验证等价类的定义,关键在于验证传递性。而这里我们需要证明的关键是,对于三个点
对于第二个问,对于这两个任意给定的开集合
题目三:令
证明提纲:由题目条件,我们得出
第二个问,我们构造函数
题目四:令
证明提纲:
为了给出一个反例,我构造了圆周上的微分同胚,满足每个点都是周期为2的周期点。同时这个微分同胚共轭于圆周的旋转,从而是结构稳定的。但是我构造出来的例子中,该圆周有非双曲的周期点,即,导数正好为
No comments:
Post a Comment