泊松括号的意义是什么？

【先来看看百度怎么定义的】

泊松括号


目录
定义


　　在数学及经典力学中，泊松括号是哈密顿力学重要的运算，在哈密顿表述的动力系统中时间推移的定义起着中心角色。在更一般的情形，泊松括号用来定义一个泊松代数，泊松流形是一个特例。它们都是以泊松（Siméon-Denis Poisson）而命名。

编辑本段导航, 搜索
跳过字词转换说明 汉漢▼▲
为了阅读方便，本文使用标题手工转换。
  • 转换标题为：简体：泊松括号；繁體：帕松括號；
  • 实际标题为：泊松括號；当前显示为：泊松括号
为了阅读方便，本文使用全文手工转换。转换内容：










  1. 简体：泊松；繁體：帕松； 当前用字模式下显示为→泊松

 [展开]  字词转换说明
字词转换是中文维基的一项自动转换，目的是通过计算机程序自动消除繁简、地区词等不同用字模式的差异，以达到阅读方便。字词转换包括全局转换和手动转换，本说明所使用的标题转换和全文转换技术，都属于手动转换。
如果您想对我们的字词转换系统提出一些改进建议，或者提交应用面更广的转换（中文维基百科全站乃至MediaWiki软件），或者报告转换系统的错误，请前往Wikipedia:字词转换请求或候选发表您的意见。





在数学及经典力学中，泊松括号是哈密顿力学中重要的运算，在哈密顿表述的动力系统中时间演化的定义起着中心角色。在更一般的情形，泊松括号用来定义一个泊松代数，而泊松流形是一个特例。它们都是以西莫恩·德尼·泊松命名的。

取决于时间的向量场演示图。泊松括号是用这个向量场的分量函数定义的。



两个取决于时间的向量场演示图，表示了上一个向量场分量的梯度函数。



两个取决于时间的向量场的叉积示意图，表示了原向量场分量的梯度函数。两个函数的括号是它们的 pq-梯度的叉积的长度。这说明了括号、梯度与叉积的关系；由无穷小梯度向量组成的平行四边形越大，括号越大。


目录

 [隐藏] 

[编辑] 正则坐标

在相空间里，用正则坐标 (q^i,p_j) ，两个函数 f(\mathbf{q},\ \mathbf{p}),\ g(\mathbf{q},\ \mathbf{p}) 的泊松括号具有如下形式：

[编辑] 运动方程

哈密顿-雅可比运动方程有一个使用泊松括号的等价表示。这可最直接地用坐标系表示。假设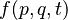 f(p,q,t) 是流形上一个函数，则我们有
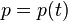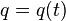然后，取 p=p(t) 与 q=q(t) 为哈密顿-雅可比方程 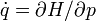\dot{q}={\partial H}/{\partial p} 与 \dot{p}=-{\partial H}/{\partial q} 的解，我们有
从而，辛流形上一个函数 f 的演化可用辛同胚单参数族给出，以时间 t 为参数。丢掉坐标系，我们有
算子 - \{\,H, \cdot\,\} 称为刘维尔算子。

[编辑] 运动常数

一个可积动力系统可能有能量以外的运动常数。这样的运动常数在泊松括号下将与哈密顿量交换。假设某个函数 f(p,q) 是一个运动常数。这意味着如果 p(t),q(t) 是哈密顿运动方程的一条轨迹或解，则沿着轨迹有 0=\frac{\mathrm{d}f}{\mathrm{d}t}。这样我们有
这里中间步骤利用运动方程得到。这个方程称为刘维尔方程。刘维尔定理描述了如上给出的一个测度（或相空间上分布函数）的时间演化。
为了使一个哈密顿系统完全可积，所有的运动常数必须互相对合。

[编辑] 定义

设 M 是一个辛流形，即流形上带有一个辛形式（闭的非退化2-形式）：\omega，这就是说 d\omega = 0 且当其视一个映射 \omega: \xi \in \mathrm{vect}[M] \rightarrow i_\xi \omega \in \Lambda^1[M]，\omega 有逆映射 \tilde{\omega}: \Lambda^1[M] \rightarrow \mathrm{vect}[M]。 这里 d 是流形 M 上内蕴的外导数运算，而 i_\xi \theta 是内乘或缩并运算，在 1-形式\theta 这等价于 \theta(\xi)。
由外微分的公理，我们由：
i_{[v, w]} \omega = d(i_v i_w \omega) + i_v d(i_w \omega) - i_w d(i_v \omega) - i_w i_v d\omega ,\,
这里 [v, w] 表示光滑向量场的李括号，其性质本质上定义了 M 上流形结构。
如果 v 使得 d(i_v \omega) = 0，我们称之为 \omega-闭（或称余闭）。类似地，如果 i_v \omega = df 对所有函数 f 成立，我们称 v \omega-恰当（或余恰当）。已知 d\omega = 0，上面的表达式蕴含着两个余闭向量场总是一个余恰当向量场，因为当 v和w 都余闭时，表达式中惟一非零项是 d(i_v i_w \omega)。又因为外导数满足 d \circ d = 0，所有余恰当向量场是余闭的；所以李括号对余闭向量场空间与其子空间余恰当向量场都是封闭。用抽象代数的话来说，余闭向量场组成了 M 上光滑向量场李代数的一个子代数，而余恰当向量场组成这个子代数的一个代数理想。
假设存在逆映射 \tilde{\omega}，M 上每个光滑实值函数 f 可以与一个余恰当向量场相伴 \tilde{\omega}(df)（两个函数与同一个向量场相伴当且仅当它们的差是 d 的核，即在 M 的任何连通分支上是常数）。这样我们定义 (M, \omega) 上的泊松括号，为可微函数上一个双线性运算，在泊松括号下 C^\infty（光滑）函数组成一个代数。它由下式给出：
\{f,g\} = i_{\tilde{\omega}(df)} dg = - i_{\tilde{\omega}(dg)} df = -\{g,f\}\,
泊松括号的反对称性由外导数的公理与条件 d\omega 保证。映为映射 \tilde{\omega} 是逐点线性和反对称的，一些作者将它们和一个双向量联系起来，这不是外微分中常见的对象。这种形式它称为这个辛流形上泊松双向量或泊松结构，泊松括号简单地写做 \{f,g\} = \tilde{\omega}(df, dg)。
光滑函数上的泊松括号对应于余恰当向量场上的李括号并继承了它的性质。从而它满足雅可比恒等式：
\{f,\{g,h\}\} + \{g,\{h,f\}\} + \{h,\{f,g\}\} = 0\,
关于一个特定的数量场 f 的泊松括号 \{f,\_\} 对应于关于 \tilde{\omega}(df) 的李导数。从而，它是一个导子，即它满足莱布尼兹法则：
\{f,gh\} = \{f,g\}h + g\{f,h\}\,
这是流形的一个基本性质，关于两个向量场的李导数运算的交换子等价于关于某个向量场的李导数，即它们的李括号。泊松括号中平行的脚色显然是雅可比恒等式的一个变形：
\{f,\{g,h\}\} - \{g,\{f,h\}\} = \{\{f,g\},h\}\,
如果 f 和 g 的泊松括号消失（\{f,g\}=0），则 f 与 g 称为互相对合（mutual involution），并有关于 f 和 g 取泊松括号的运算交换。

[编辑] 李代数

泊松括号是反交换的，也满足雅可比恒等式。这使得辛流形上的光滑函数空间成为无限维的李代数，以泊松括号为李括号。相应的李群是辛流形的辛同胚群（也称为正则变换）。
给定一个可微切丛上的向量场 X，令P_X为其共轭动量。这个从场到共轭动量的映射为从泊松括号到李括号的李代数反同态：
\{P_X,P_Y\}=-P_{[X,Y]} \,。
这个重要结果值得我们给个简短证明。记位形空间的 q 点的向量场 X 为
X_q=\sum_i X^i(q) \frac{\partial}{\partial q^i}
其中 \partial /\partial q^i 是局部坐标系。X的共轭动量的表达式为
P_X(q,p)=\sum_i X^i(q) \;p_i
这里 p_i 为和坐标共轭的动量函数。这样就有，对相空间的每点 (q,p)，
\{P_X,P_Y\}(q,p)= \sum_i \sum_j \{X^i(q) \;p_i, Y^j(q)\;p_j \}
= - \sum_i p_i \; [X,Y]^i(q)
= - P_{[X,Y]}(q,p) \,
以上对所有 (q,p) 成立，证毕
【笔者也是什么也看不懂，本科三年物理专业学了吗？！也不能这样说，至少做了点习题，，还是说说个人理解吧……
经典的体系需要坐标表述q1 q2 q3 p1 p2 p3 等等，时间是经典力学中处于中心地位的物理量。一切物理量都可以写成时间的函数。那么q(t) p(t)一旦确定，体系就确定无疑了。
体系要满足一定的演化方程，而演化就是随着时间t演化，与这个中心地位时间t关系的物理量还有一个叫做哈密顿量H，这个演化方程说的就是H t p q的关系。
举一个例子:
H=H(t)    q=q(t)     p=p(t) 是未知的三个物理量
①哈密顿方程
如果给定H=p*p+q      q(0)=2    p(0)=1
就可以解出来这个体系了。
其他力学量如果都可以写成A=A(p,q,)的形式，
对A求全微分，再利用①哈密顿方程，自然可以得出
dA/dt=[A,H]，泊松括号的背后是省略的q和p，
使用一个不恰当的比喻——国家的领导人的本质是人们的大众捧场捧出来的！两位国家元首会晤时的友好程度本质上时其民间经济、文化、科技交流程度的体现。
一个体系的力学量，例如角动量J，能量E，磁矩M等等，
如果能够和H对易，[J,H]=0  某种程度上，说明了合成这些力学量的“最基本坐标”有着相通性。不恰当的例子：新加坡的每个国民同时都是中国国籍，那么[新加坡,中国]=0 是对易的，中国人不饿肚子时，新加坡人也就不饿肚子了，即当H和J对易时，H如果守恒，J也守恒。
泊松括号对易的例子还有一个，这是听某个老师在量子力学上课讲过的，说某快餐店有很多份套餐，套餐A={苹果、面包、牛奶、香肠}    套餐B={香蕉、牛奶、饼干}   套餐C={香蕉、饼干}  于是又A与B不对易 B和C对易   这个例子阐述测不准原理——苹果和香蕉不可兼得。然而，我觉得这个对易也有点关系吧——组成套餐的基本成分不同。

当然，经典力学中坐标都是连续的实数的一部分。经典力学上泊松括号的对易性体现在两个力学量的内在联系。(可能数学上说的什么空间、流形、映射就指的是这种内在联系）
[Lx,Ly]=[yPz-zPy,zPx-xPz]=Lz
这个式子，以x y z Px Py Pz为基础的空间，三个方向的角动量之间是由内在的联系——我们拿一本书，先沿着x轴转动，再沿着y轴转动，某种情况下可以等效为沿着z轴的转动。
[x,y]=0  但是，你拿一本书，先沿着x方向平移，再沿着y方向平移，是没有任何可能指望通过沿着z方向等效的。
这些例子说明，泊松括号可以判断力学量之间的某种内部属性关系


元素是A B等等，乘法定义为[A B]
又泊松括号若干性质决定它是个李群，（李群是什么东西？，完全不懂……）
既然是个群，群应该有个单位元：满足dI/dt=[ I ,H ]=H
解出来的东西是就哈密顿量的积分，I=∫Hdt，这种东西在量子力学中好像有点意思（我也不懂），
通过求解特殊方程得到的单位元I=∫Hdt还无法令人完全信服。可移动过例子验证一番……
另一个推理是，I这个东西和谁作用就是谁，也它玄妙了！



*********************************************************************************************
（以上全都是民科在扯淡  不要轻信 ）