London equations
From Wikipedia, the free encyclopedia

As a material drops below its superconducting critical temperature, magnetic fields within the material are expelled via the Meissner effect. The London equations give a quantitative explanation of this effect.
Contents
[hide]Formulations[edit source | edit]
There are two London equations when expressed in terms of measurable fields: is the superconducting current density, E and B are respectively the electric and magnetic fields within the superconductor,
is the superconducting current density, E and B are respectively the electric and magnetic fields within the superconductor,  is the charge of an electron & proton,
is the charge of an electron & proton,  is electron mass, and
is electron mass, and  is a phenomenological constant loosely associated with a number density of superconducting carriers.[6] Throughout this article Gaussian (cgs) units are employed.
is a phenomenological constant loosely associated with a number density of superconducting carriers.[6] Throughout this article Gaussian (cgs) units are employed.On the other hand, if one is willing to abstract away slightly, both the expressions above can more neatly be written in terms of a single "London Equation"[6][7] in terms of the vector potential A:
London Penetration Depth[edit source | edit]
If the second of London's equations is manipulated by applying Ampere's law,[9]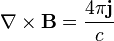 ,
,
 , over which external magnetic fields are exponentially suppressed. This value is the London penetration depth.
, over which external magnetic fields are exponentially suppressed. This value is the London penetration depth.A simple example geometry is a flat boundary between a superconductor within free space where the magnetic field outside the superconductor is a constant value pointed parallel to the superconducting boundary plane in the z direction. If x leads perpendicular to the boundary then the solution inside the superconductor may be shown to be
Rationale for the London Equations[edit source | edit]
Original arguments[edit source | edit]
While it is important to note that the above equations cannot be derived in any conventional sense of the word,[10] the Londons did follow a certain intuitive logic in the formulation of their theory. Substances across a stunningly wide range of composition behave roughly according to Ohm's law, which states that current is proportional to electric field. However, such a linear relationship is impossible in a superconductor for, almost by definition, the electrons in a superconductor flow with no resistance whatsoever. To this end, the brothers London imagined electrons as if they were free electrons under the influence of a uniform external electric field. According to the Lorentz force lawTo obtain the second equation, take the curl of the first London equation and apply Faraday's law,
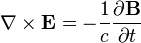 ,
,
Canonical momentum arguments[edit source | edit]
It is also possible to justify the London equations by other means.[11][12] Current density is defined according to the equationReferences[edit source | edit]
- ^ London, F.; H. London (March 1935). "The Electromagnetic Equations of the Supraconductor". Proc. Roy. Soc. (London) A149 (866): 71. ISSN 0080-4630.
- ^ Michael Tinkham (1996). Introduction to Superconductivity. McGraw-Hill. ISBN 0-07-064878-6.
- ^ Neil W. Ashcroft; N. David Mermin (1976). Solid State Physics. Saunders College. p. 738. ISBN 0-03-083993-9.
- ^ Charles Kittel (1999). Introduction to Solid State Physics. ISBN 0-47-141526-X.
- ^ Meissner, W.; R. Ochsenfeld (1933). "Ein neuer Effekt bei Eintritt der Supraleitfähigkeit". Naturwissenschaften 21 (44): 787. Bibcode:1933NW.....21..787M. doi:10.1007/BF01504252.
- ^ a b James F. Annett (2004). Superconductivity, Superfluids and Condensates. Oxford. p. 58. ISBN 0-19-850756-9.
- ^ John David Jackson (1999). Classical Electrodynamics. John Wiley & Sons. p. 604. ISBN 0-19-850756-9.
- ^ Michael Tinkham (1996). Introduction to Superconductivity. McGraw-Hill. p. 6. ISBN 0-07-064878-6.
- ^ (The displacement is ignored because it is assumed that electric field only varies slowly with respect to time, and the term is already suppressed by a factor of c.)
- ^ a b Michael Tinkham (1996). Introduction to Superconductivity. McGraw-Hill. p. 5. ISBN 0-07-064878-6.
- ^ John David Jackson (1999). Classical Electrodynamics. John Wiley & Sons. pp. 603–604. ISBN 0-19-850756-9.
- ^ Michael Tinkham (1996). Introduction to Superconductivity. McGraw-Hill. pp. 5–6. ISBN 0-07-064878-6.
- ^ L. D. Landau and E. M. Lifshitz (1977). Quantum Mechanics- Non-relativistic Theory. Butterworth-Heinemann. pp. 455–458. ISBN 0-7506-3539-8.



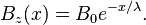


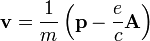

No comments:
Post a Comment