Saturday, October 4, 2014

不能被不交的开集所分离，所以L不是豪斯朵夫的。它是一个拓扑流形，但不是豪斯多夫拓扑流形

什么是流形的豪斯多夫假设，高手解决一下！：

两个原点的线
我们在这里给出一个空间的例子，它满足拓扑流形所有的条件，除了它不是豪斯多夫空间(Hausdorff space)。取两个R的拷贝，把它们写作

and

并定义如下等价关系

if

从这个等价关系得到的商空间L是一个象实直线那样的空间，除了有两个点"占据"了原点。特别的是，它们不能被不交的开集所分离，所以L不是豪斯朵夫的。它是一个拓扑流形，但不是豪斯多夫拓扑流形。

经常，拓扑流形被定义为必须是豪斯多夫的，在这个定义下，上面的例子不是流形。

不一样的贪吃蛇

陳浩 · 6 个月前

这个专栏文章由问题「莫比乌斯带上的棋盘？」引发。其中内容我很确定在某个答案里写过，不过找不着了。莫比乌斯带，克莱因瓶等，看着非常高大上，其实把正方形的四边做合适的粘连就可以得到了。下面五个图来自维基百科的相关页面，每个图上我都大致画了「一条」带方向的线段（黑色细线，可能不是很直）。你看的出这些分别是什么曲面吗？
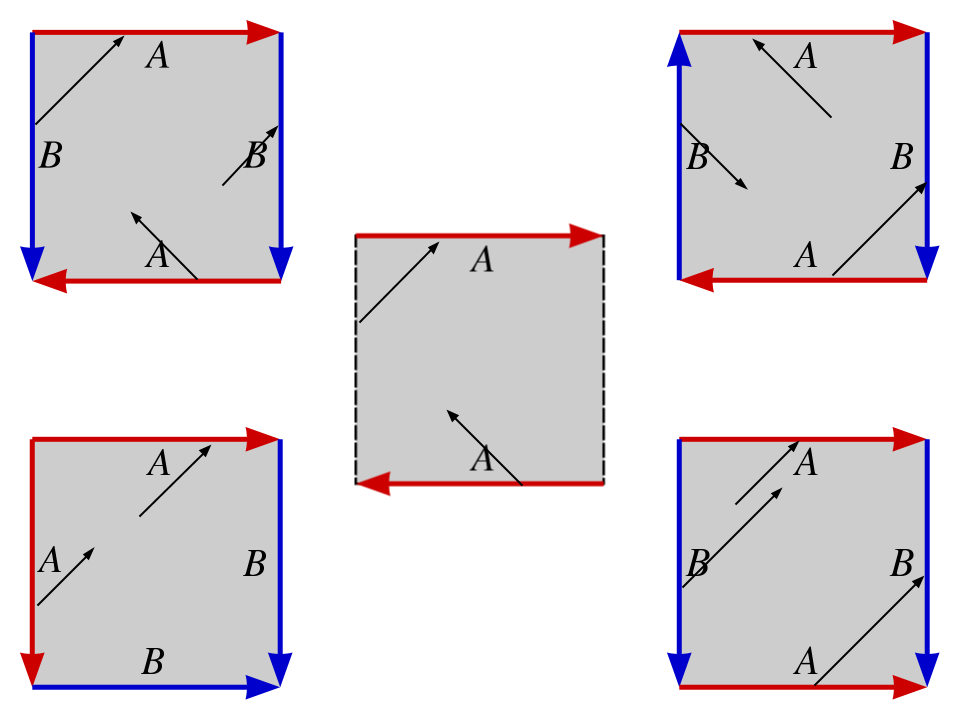图中正方形的边界都用红色或蓝色的箭头标注，表示同色的边界按标注的方向粘合。
先看右下角的图
设正方形左下角坐标 (0,0)，右上角坐标 (1,1)。因为上下边界被粘合起来，坐标为 (x,1) 的点被等同于坐标为 (x,0) 的点。同样的，左右边界被粘合起来，所以坐标 (0,x) 的点被等同于坐标为 (1,x) 的点。
试想我所画的黑线是一个正在走直线的贪吃蛇的路径。它向右上方行进，先碰到了上边界，于是从下边界同样的横坐标处出现，继续向右上方行进，碰到右边界，然后从左边界同样的高度出现，继续向右上行进。这是大家非常熟悉的情景，有些地方叫作「周期性边界条件」。
这是什么曲面呢？很容易想象……把正方形卷成一个筒，然后再把两端接起来……没错这是一个 torus（轮胎面？甜甜圈面？）
再看左下角的图
根据标注的箭头， (0,x) 被等同于 (1-x,1)，(x,0) 被等同于 (1,1-x)。这是什么曲面呢？球面。也许换个角度就更加明显了：是想一个地球，左上角是北极，右下角是南极，而 (0,0)-(1,1) 这条对角线是赤道。而左边和下面的边界，分别等同于上面和右边的边界，是「国际日期变更线」。
再看中间那幅图
根据标注的箭头，左右边界没有粘合。而上下边界，注意粘合的方向：(x,0) 被等同于 (1-x,1)。我所画的贪吃蛇，先是向右上方向行进，在偏左的地方碰到了上边界。于是他从下边界偏右的地方出现，向左上方向行进。这是什么曲面呢？注意粘合的方向是反的，是「扭」了一下再粘起来的。这正是莫比乌斯带。
现在你们知道怎么玩了，其实就是玩贪吃蛇的时候加上个变态的边界条件而已。上方的两幅图我就直接公布答案了：他们分别是克莱因瓶和射影平面。如果有人设计出这样的贪吃蛇，不知会不会流行。很有挑战不是吗？
对于数学基础不错的同学们来说，这也许太简单了。我就再贴两个当年初学时颇耗了我一些脑细胞的曲面。第一个是二维的 Dunce hat (topology)：

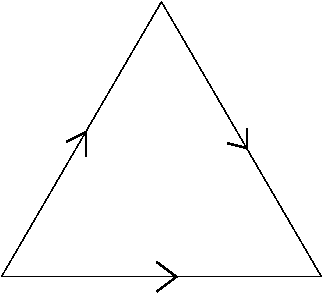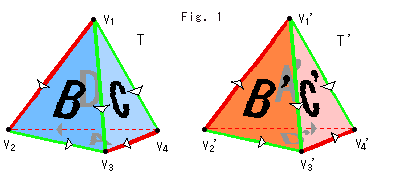
这三条边要全部按给定的方向粘合起来，三个点也因此相互等同。因此最后的结构中只有一个点，一条边，一个面。其实粘合左边和下边还是比较容易想象的，结果是一个圆锥。然后右边要怎么处理呢？想要直观可以看这个视频 https://www.youtube.com/watch?v=34j4CppfRTA 他在一块布上缝了两个拉链，做出了这个曲面。结果是一个很萌很萌的睡帽。
第二个是粘合两个四面体得到的三维流形，图片来自：Figure-8 Knot (2)