物理学笔记（6）：基尔霍夫定律的“盲点”
精选
|||
物理学笔记（6）：基尔霍夫定律的“盲点”
不得不说，我是一个无聊的人......
曾经有位初三的小朋友来问我电路问题。这位小朋友物理基础似乎不错（至少初中物理基础），这诱使我产生了做个“小试验”（不是“实验”！）的冲动，于是乎故作神秘告诉他：我现在传你一个一劳永逸的“秘术”，但你到上大学之前，只能在草稿纸上演算，万不可轻易示人。如果你不听我的，考试扣分别怪我哦！——估计许多朋友已经猜到：所谓“秘术”，不过就是电路拓扑的基尔霍夫定律（KCL & KVL）罢了——我以为，就直流电路的情况而言，一位数理基础良好的初中生完全可以掌握它。
不出所料，小朋友掌握的情况还不错，即使这个两个定律在他上大学前所遇到的电路求解问题中并不实用——除了一些简单的电桥电路外，在初高中阶段使用KCL和KVL，甚至还有点儿“脱了裤子放屁”（谁叫我这么无聊呢！），就算他有点儿“无用的收获”吧。
其实，真正的收获是我的，虽然微乎其微：由于他们在初中阶段遇到的电路都是“理想电路”（即考虑内阻或内压降为零的“理想电源”），在解算过程中，我不经意地意识到了基尔霍夫定律一个非常隐蔽的“盲点”。之所以隐蔽，是因为我们在使用基尔霍夫定律是主要面对的是“实际电路”，这使得该“盲点”被自然地规避了。换句话说，在实际问题中，无论你有没有意识到这个“盲点”，一般不影响电路的求解——要不然怎么说我很无聊呢？
我们现在使用的基尔霍夫定律是古斯塔夫·基尔霍夫（ Gustav Kirchhoff）于1845年提出的，它一般被表述为两个定律：基尔霍夫第一定律，也叫电流定律（KCL）；基尔霍夫第二定律，也叫电压定律（KVL）。
对一个占据空间体积的V闭合曲面（高斯面）S，由电荷守恒定律易知：S内单位时间减少的电荷等于单位时间从边界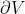
流出的电荷，即
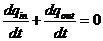
引入电流强度定义，则
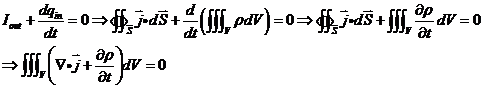
由此可得到电荷守恒的数学表达式——电流连续性方程，取其微分形式为：
对某一电流场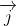
，若任意高斯面内
，则有描述此类电流场的稳恒电流条件：
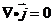
电荷守恒定律在稳恒条件下可充分导出电路学中的基尔霍夫第一定律：任一节点处的各电流的代数和等于零，即
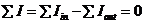
也就是说，KCL本质上是电荷守恒定律在电路中的反映。
KVL则是能量转化与守恒定律在电路中的反映。根据静电场（有势而无旋）的安培环路定理，结合部分电路的欧姆定律的积分形式（也就是初中物理教的欧姆定律）I=U/R，可以很容易得到基尔霍夫第二定律：对任一闭合回路，各支路上的电压代数和等于零，即
KCL和KVL究其本质，都是对称或守恒，且是一种动态的守恒：前者“有进有出”，后者“有升有降”。就其守恒本质和在稳恒电路的应用，初中生是可以掌握的。
我们有必要保持审慎：物理学中不存在“放之四海而皆准的真理”。关于基尔霍夫定律的适用条件，一般文献（教材）给出类似这样的说法：原则上它可以用来解算任何复杂电路（当然在推广到交流的情形时，应引入含时电荷密度和元件电感的修正）。
我一般比较警惕有“全称量词”（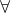
）与“必然模态”（
）的论断表述，比如周衍柏先生的《理论力学教程》中的表述（p326）：哈密顿原理是和牛顿运动定律等价的原理......甚至牛顿运动定律也可认为是哈密顿原理的必然结果——我就持保留意见，至少“牛三”应视为基本的实验定律。
那么基尔霍夫定律的“盲点”在哪儿？
——基尔霍夫定律不适用于存在零电阻回路的电路。比如下图：
若并联的两个电源为零内阻的理想电源，则电路存在一个零电阻回路（虚线箭头所示）。此时，除非两个电源输出的路端电压（理想电源，路端电压=电源电动势）相等，基尔霍夫定律不适用。
补记：
感谢各位老师补充指正！
其实所谓基尔霍夫定律的“盲点”，或者说零点阻回路，正是理想电路模型的“奇点”——我时常强调“奇点意识”，在这里却把它“忽略”了，实在不应该！
这个纯属臆造的“电路”，是否类似于“克里特人”或者那位脾气古怪的“理发师”呢？？？
根据部分电路的欧姆定律
R=0这个“奇点”是十分明显的，在实际情况中，即R足够小（小到在实验中可以忽略），它的物理意义一般理解为元件的“短路”（若U足够大则意味着“击穿”）。
而在通常的电路分析中，理想电路模型无法给出自由电荷的微观运动图像。基尔霍夫定律在零电阻回路的失效，其实是理想电路模型在“奇点”失效了——微观图像则需要依赖其他模型近似给出，比如在经典情况下，金属电子论给出的电流微观表达式（当然固体物理中还有其他模型近似）
其中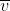
为载流子的迁移速率，是外场与介质（晶格）阻碍的结果，是一个平均速率而非瞬时速率。关于此中“细节”，L.Cooper在《物理世界》（An Introduction to the Meaning and Structure of Physics的中译本）中是这么说的（p350~251）：
如果在导线的两端加上电位差，导线中就会产生电场，也就是说，将有一个力开始作用于电子。倘若电子可以自由运动，那么它的加速度将等于a=F/m=eE/m，此时它的速度将不断地增大。结果是，电流将随时间和增长。这种景象可以在所谓理想导体中观察到。在这个意义上，普通的金属都不是理想导体。一般说来，在一个稳定的电位差作用下将产生一个稳定的电流，也就是说，导体中的电子以某个不变的平均速度运动。产生这种情况的原因之一是，电子与物质中的杂质不断碰撞。开始时，电子被加速，但通过某个平均自由程距离以后，电子与杂质相碰撞并失掉它的平移运动的大部分能量。然后，它又开始重新加速，如此等等。其结果是，电子以某个平均速度朝着电场引起的力的方向运动，因而出现某个平均电流。这个结论与观察结果一致，即纯材料的导电性能优于有杂质的同类材料。
当我们把一个固有理论（定律、公式或模型）推演到“奇点”附近时，“风险”极大，务必慎之又慎，慎之又慎，当引以为戒！
http://blog.sciencenet.cn/blog-217073-840528.html
上一篇：男儿何不带吴钩：说说文人与军事（上）
下一篇：星空立法者——从第谷到开普勒
22 陈楷翰 尤明庆 文克玲 钟炳 沈律 王春艳 黄永义 张云 周金元 李维纲 钱磊 樊京 张操 罗教明 郭景涛 罗会仟 徐传胜 yunmu xiaoban95 jianhuajiang ychengwei ybyb3929
该博文允许注册用户评论 请点击登录 评论 (24 个评论)
- [24]王国强
- "结果是，电流将随时间和增长。这种景象可以在所谓理想导体中观察到。“
？？？
既然是理想导体，那是怎么实现观察的？ - 博主回复(2014-11-5 20:37)：比如伦敦方程描述的理想情况？
- 博主回复(2014-11-5 19:58)：我估计Cooper的意思应该是一次“思想实验”的观测吧
- [23]李维纲
- 对于涉及巨大量子数之宏观物体的宏观运动，量子力学必须给出和客观现象一致的结论，这没有什么值得惊叹的。罗教明老师令人惊叹的重要成果在于，他将经典力学和麦克斯韦尔方程组贯彻到了微观领域！或者说，罗老师不是将经典力学统一于量子力学；而是将量子力学统一于经典力学和电磁学！这实在是极其值得关注的理论成果。
- [22]杜敏彪
- 一切都在振荡，模糊了焦点。
http://cell.bio1000.com/cell-reports/201410/192.html
- [21]郭景涛
- 我认为楼主的例子不能算是基尔霍夫定律的奇点。这个例子逻辑上不满足矛盾律。先不要说实际上是否可能，逻辑上先已经不可能了。毕竟，事实可能应该是逻辑可能的子集（也许这是属于信仰范畴）。你认为这个例子至少在概念上是存在的，只不过是因为你是以图形方式表述这个例子。试想，用一种语言来描述这个网络，某个节点先被赋值为10V，在被赋值为5V，那么10V就被5V刷新了。
- 博主回复(2014-11-3 17:44)：这个例子并不是“奇点”，“奇点”来自于理想电路模型的方程（R=0）。您给出的的网络节点赋值的表述，实际上已经使用了“等效”的办法，把电源的细节“滤掉”了，自然就没有这个问题了。
- [20]郭景涛
- 9楼切中肯綮
- 博主回复(2014-11-3 17:13)：其实这就是借电路的例子说模型的“奇点”罢了
- [19]罗教明
- 我在【17】楼表达的核心观点是，零电阻导线的两端，从物理的角度是施加不了电位差（电压）的，数学奇点是由于U不为零，R为零，纯数学条件导致的，真实情况是不可能的。因此我们在讨论一件自然界中，不可能发生的现象。所以，奇点解，在数学逻辑上是成立的，但没有物理意义。
- 博主回复(2014-11-3 17:05)：固有模型的“奇点”预示着适用范围更广的新模型
- [18]ybyb3929
- 这篇博文，我左看，右看，博文的核心观点不就是曾经在百度贴吧中被官科们视为民科的观点吗
- 博主回复(2014-11-3 17:04)：我确实是“民”，但不敢自称“科”，况且我对批判“旧理论”或构造各色“新理论”没什么兴趣
- [17]罗教明
- 李老师的例子很有启发意义。理解一个物理定律的数学表达式时，要与物理现象紧密联系，就不会产生歧义。
载流子（电子）通过导线会受到阻力的影响，因此要维持一个稳定的电流需要施加一定电场，导线的阻抗越大，电场强度越高；从能量的角度来理解，导线的电阻越大，消耗的能量越多，要维持电流的稳定，导线两端施加的电位差就越高。
如果导线的电阻为零，如超导体，就不会消耗能量，导线中处处电位相同，是个等位体。此时，也不需要在导线两端施加电压来维持电流稳恒流动。
我想这样来理解欧姆定律，当电阻为零时，就不会产生奇点的理解困难了。 - 博主回复(2014-11-3 17:03)：可能什么时候把超导机制理解透彻了，才能真正把握常规导体的导电机制吧。
- [16]张操
- 很好的问题。理论物理学家经常在奇点上犯错误。
- 博主回复(2014-11-3 17:01)：讨论“奇点”附近的情形，有较大风险
- [15]ybyb3929
- “甚至牛顿运动定律也可认为是哈密顿原理的必然结果——我就持保留意见”——保留意见很支持，理由见：http://tieba.baidu.com/p/2666794024
- [14]ybyb3929
- 另外，还有数学表达式未必一定能表达物理本意
- [13]ybyb3929
- 这种现象太多了，这其实是理想模型带来的
- [12]樊京
- 很多人将坡印廷能流的概念推广到直流电情况。而我们知道，直流电并不存在波动。请问李老师，“静态坡印廷”能流算不算是“动态坡印廷”能流的一个“奇点”呢？
- 博主回复(2014-11-3 17:00)：樊老师，您提到的问题我目前还没有特别清晰的看法，容我再想想。
就我现在所想到的，我们最直观的电路能量转化与守恒的分析基于经典电子论模型，而经典电子论模型在理解电路导电过程中，忽略了磁场，这在分析电容器这类元件时会带来障碍，所以麦克斯韦引入电位移矢量和位移电流来描述，这就要依赖于电磁场模型。在电路问题中，电磁场模型应该比经典电子论模型提供更详细的微观图像。至于坡印廷矢量所描述的周围空间电磁场和电路之间的能量交换，此中细节，我还要再琢磨琢磨。
- [11]李维纲
- 如果老师能用它把光学、电磁学等分散在各个课程的相应规律“串”起来，一以贯之，至少经典物理学的结构就比较清晰和明朗了。
——————————————————————————————————————
的确如此！并且按照罗教明老师的观点，量子力学也可以还原为经典力学和麦克斯韦尔方程组。这是极其重要的理论成果。 - 博主回复(2014-11-3 16:45)：系统量子数足够大而变量足够小的情况下,量子力学的结论应与经典物理的结论一致。这是玻尔的对应原理。
- [10]xiaoban95
- 高三学生，自认为对中学物理还好，但是表示上面的看不懂。
高三学生不可爱，也没有初中的孩子那么纯真。哎。。。怎么办呢没人爱呢
- 博主回复(2014-11-3 16:43)：高中应用基尔霍夫定律不存在障碍，更深入的理解和推导，需要高等数学的知识。
- [9]ep4h
- 你把电压不同的两个理想电压源并在一起，估计任何物理定律都会失效。
集总线路本身就是一种理想化，你在理想线路模型中把不同电源并在同一节点，就相当于数学上即定义U=10又同时定义U=5，不可能不产生矛盾。也就是说，这种矛盾其实是逻辑性的，而不是物理性的。 - 博主回复(2014-11-2 20:45)：是啊，理想电路模型并没有提供这种限制，这当然只能导致一个逻辑性的矛盾（这种矛盾出现的地方，就是固有模型失效的地方），因为实际情况中，不可能会出现U=10V又同时U=5V的情况。
- [8]yao101yao
- 看数学公式就头疼
- 博主回复(2014-11-2 21:28)：是啊，但若是没有数学表述，表达就很难聚焦到具体的某一点
- [7]王春艳
- 理想状态是对不理想状态的合理简化近似状态，我觉得是不是不能编造理想状态啊？
- 博主回复(2014-11-2 20:50)：我觉得我“编造”的这个“理想状态”，就类似于罗素“编造”的“以自身为元素的集合（或者说“类”）”
- 博主回复(2014-11-2 18:53)：我悔过,我疏忽了自己经常说的奇点问题,太愚蠢了。我要加个补正。
- 博主回复(2014-11-2 18:53)：我悔过,我疏忽了自己经常说的奇点问题,太愚蠢了。我要加个补正。
- [6]张江敏
- 极端情况不能孤立地考虑，应该作为一般情况的极限考虑。
- 博主回复(2014-11-2 17:40)：看来我确实表达得不清楚,我想说的人是理想电路模型在这种情况下失效了,稍后我好好改改。
- [5]文克玲
- 物理“零”不是数学“零”。
物理“零”是“可以忽略”的意思。
所给情况，电源内阻不能忽略。 - 博主回复(2014-11-2 17:38)：是这样的,我想表达的就是理想电路模型的失效(不能忽略电阻),看来我表达的不是很清楚。
- [4]徐晓
- 电路没学好的必然结果。实际上电阻为零，电子做加速运动，所以加速过程等效为一个电阻。
- 博主回复(2014-11-2 17:36)：我认为这是理想电路模型失效的问题,理想电路模型无法提供电荷运动的微观图像
- [3]王虹宇
- 你这样连接,两个电源有一个要烧掉....
- 博主回复(2014-11-2 17:42)：现实中不允许这种电路,理想模型失效了
- [2]尤明庆
- 李老师好。
在满足节点电流之和为零的条件下, 实际电流使得整个电路消耗的功率最小.
那么, 利用Lagrange 条件极值就很容易写出方程。
我觉得，大学物理应该介绍相关知识（我的同学说不知道），这样便于理解弹性力学的极小势能原理。 - 博主回复(2014-11-2 20:35)：电荷运动的实际路径也满足变分原理，这也是体现分析力学（最小作用量原理、哈密顿原理......）威力的地方。
我觉得自己当年学的《理论力学》（特别是分析力学部分）要么过于抽象，要么局限于运动学、静力学和动力学，如果老师能用它把光学、电磁学等分散在各个课程的相应规律“串”起来，一以贯之，至少经典物理学的结构就比较清晰和明朗了。
- [1]陈楷翰
- 妈呀，又是数学公式。。。。。
- 博主回复(2014-11-2 20:26)：便于记录嘛
No comments:
Post a Comment