精选
|||
正电子 = 逆着时间的负能量电子
那么 逆着时间的普通电子 = 负能量的正电子
不过注意，这些负能量态本身都是从没有观察到的，不一定具有物理意义的数学解
德布洛依提出物質波的概念
物質波的波長與動量呈反比
所以動量越大 物質波的波長越小 波長越小性質越接近粒子
物理学笔记（5）：信动量，得中子
一、从“牛二”到动量守恒
上回说到：玻尔的定态跃迁理论通过初末定态的差量与辐射建立联系，从而规避了过于复杂的内部细节。这种“技巧”（还有类似的诸多数学手段）并不独属于量子力学，在经典力学中也常“出没”——其中有一些在经典力学中业已成熟（比如微分方程的本征值问题），另一些则是现代物理方法确立后引入的修正（比如狄拉克函数）。
早期量子论的定态跃迁和经典力学中的功能关系针对的都是能量或具有能量量纲的物理量。在力学中，除能量外，动量也是一个十分重要的状态量（本文只讨论线动量Linear Momentum）。我们对动量的处理仍然可以用初末态差量反映过程量，就规避复杂的动力学细节（比如某个作用过程的平均作用力）这一点而言，好处是明显的。
在牛顿理论体系中，“动量”或者说“运动的量”（quantity of motion）是一个基本物理量，甚至可以说牛顿理论是围绕动量展开的。“力”的基本物理量“地位”是在分析力学的静力学体系中得到强化的。在成熟的分析力学体系（拉格朗日力学与哈密顿力学）中，能量以及具有能量量纲的拉格朗日函数和哈密度函数（作为动力学方程的首次积分）成为了基本物理量。
今天绝大部分力学（高中物理、普通物理、理论力学）教材在引入“动量”的时候，一般都是直接用标量m（质量或惯性质量）和矢量v（速度）做内积：p=m·v ——牛顿本人在《原理》（《自然哲学的数学原理》）中也是这么干的。按今天的视角：这种表述形式基于对惯性质量的处理，即确定物体的惯性质量与运动无关，其值不随时间变化。当然这种表述也不适用于非相对论性变质量（其实是“物质的量”发生改变）物体的动力学问题，比如齐奥科夫斯基讨论的火箭方程。
在更普遍意义上理解动量，需要回溯到原始版的“牛二”——在他本人的“牛顿第二定律”表述中（见《原理》的英译版：Newton, Isaac, Newton's Principia : the mathematical principles of natural philosophy, New York: Daniel Adee. 1846）：
The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.（运动的变化正比于外部所施加的力，变化方向沿外力作用线方向。）
用数学公式可以表达为：dp=F·dt，整理得：
即：外力是动量随时间的变化率。我们今天广泛使用的“牛二”形式（F=m·a 或
，可以称为“欧拉形式”）是欧拉于1750年给出的——在惯性质量不随运动时间变化的前提下，将p=m·v代入“牛顿形式”。
“牛二”的“欧拉形式”是经典动力学的基本方程，而“牛顿形式”则具有更普遍的适用性。后者的“奇妙”在于：它完全符合后来狭义相对论的要求，也就是说“欧拉形式”只适用于经典力学，而原始的“牛顿形式”既满足经典力学，又满足狭义相对论——费曼在他的《讲义》中把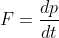
、洛伦兹力公式、牛顿万有引力公式与麦克斯韦方程组并列为“经典（非统计性）物理学基本规律”。
以动量为态函数处理具体问题时，规避复杂动力学细节的办法主要是使用“动量守恒定律”：根据“牛二”的原始形式，当外力F=0时，物体动量随时间的变化率为0，即物体动量在个过程中为常量——在仅有两个质点相互作用的简单模型中，费曼用“牛二”和“牛三”给出了一个十分简单的构造方法（见《讲义》）：
推广到质点组模型中，即普遍的动量守恒定律。
在分析力学中，根据诺特定理（Noether’s theorem）：每一种对称操作对应于一个物理量的守恒，动量守恒实质是“机械能对空间平移具有对称性”——在稳恒场中的简单机械运动情况下，机械能E=E(x,vx)，重力势能V=V(x)，则
正如机械能守恒有其适用条件，动量守恒亦然。许多教材把动量守恒的条件记为：质点或质点组不受外力或所受合外力为零。应当说，这个条件在理论上是准确的，但在实际应用中往往达不到：
我们知道加速度作为速度随时间的变化率（速度关于时间的一阶导数，即速度变化快慢），在某个时刻（不是一段“时间间隔”）并不能反映速度的变化。类似地，合外力作为动量关于时间的一阶导数，不能直接导致动量的改变。合外力必须在一段时间上做积分（即力在时间上的累积）才能改变态函数动量，这个积分被定义为一个过程量——冲量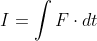
，对同一个物体或研究对象有：
即所谓的“动量定理”。
在实际问题中使用动量守恒时，合外力为零的情况极其罕见。动量守恒成立的条件应“弱化”为：合外力产生的冲量为零——它的“操作性”定义为：质点间相互作用的时间间隔足够小，以至于合外力产生的冲量近似为零（这种境况下一般意味着内部相互作用力远远大于合外力）。例如碰撞、爆炸、反冲等物理过程中，在整个时间间隔内，合外力一般不为零（特别是重力存在的情况下），如果时间间隔足够小（口语表达的“瞬间”，意味着物理变化过程十分剧烈），我们可以认为合外力的冲量近似为零，故在这个“瞬间”使用动量守恒。
使用动量守恒或冲量定理都可以从初末态函数入手，尽量避免讨论质点间复杂的动力学过程。这个优势在两个质点相互作用情况下倒还不十分明显，但如果你面对的是质点组，即多个物体间的相互作用过程，它可以帮你尽量避免陷入“万劫不复”的“N体运动”——如果简单的方法能达到效果，千万不要“舍近求远”。比如一道很经典的运动学问题：两个人分别匀速相向而行，一只苍蝇以匀速率在他们中间做往复运动，要求苍蝇运动的总路程。“传说”（只是传说！），冯·诺依曼被问到的时候是用“级数求和”的办法快速“心算”出结果的（这也不是常人能达到功力，甚至极有可能是诺依曼本人的“调侃”），而实际上，只要抓住三者整个运动时间相同，用最基本的运动学公式就能快速求解——现在，这个题估计小学生就会遇到。
二、查德威克：信动量，得中子！
上帝总是不断地抛出“苹果”，但不是所有人都接得到！
1920年，玻尔的“大师兄”卢瑟福在确定质子存在后，预言了一种来自原子核的电中性“辐射”。
1931年到1932年，普朗克的高足瓦尔特·博特（W.Bothe）与其弟子赫伯特·贝克（H.Becker），出身显赫的“小居里夫妇”（约里奥—居里夫妇，the Joliot-Curies）的关注焦点都集中在了氦核轰击铍原子的反应：
他们分析的结果表明：观测到的中性辐射n是一种
辐射——他们已经“看见”了中子，但并没有“抓住”它！——最终便宜了“英国佬”！
阅读了小居里夫妇发表的论文后，卢瑟福的高足查德威克（James Chadwick）在不到一个月的时间内完成了一系列实验(不能忽视卢瑟福打下的基础！)，并于《自然》上发表了一篇简短的文章《中子可能存在》（Possible Existence of a Neutron，Nature, p.312 ，Feb. 27, 1932）。更系统的工作发表在当年的《皇家学会通报》（Proceedings of the Royal Society A — Mathematical, Physical & Engineering Sciences），题目去掉了possible（底气十足！），改为《中子的存在》（the Existence of a Neutron，Proc. R. Soc. Lond. A，vol.136, p.692~708, 1932）——这两篇文章今天被视为“中子”的“准生证”！
其实“英国人”并不比“德国人”或“法国人”高明多少。
十九世纪末到二十世纪初，同志们见识了太多令人眼花缭乱的实验结果和理论推导——连玻尔都一度认为，被大家奉为“铁律”的能量或动量守恒只有在统计平均的意义上才是守恒的——宗师也有“跑偏”的时候啊！
查德威克同志（算是玻尔的师弟）的工作表明：眼花缭乱的时候，不要急于构造“新理论”。他在两篇文章中明确地阐述了自己的基本思路：
Up to the present, all the evidence is in favour of the neutron, while the quantum hypothesis can only be upheld if the conservation of energy and momentum be relinquished at some point.（Possible Existence of a Neutron）
直到目前, 所有的现象都有利于中子假设, 而量子假设（即辐射的光量子）只有在废除能量与动量守恒才成立。
It is evident that we must either relinquish the application of the conservation of energy and momentum in these collisions or adopt another hypothesis about the nature of the radiation. If we suppose that the radiation is not a quantum radiation, but consists of particles of mass very nearly equal to that of the proton, all the difficulties connected with the collisions disappear,.......(the Existence of a Neutron)
实验表明：在这些碰撞过程中，我们要么放弃应用能量与动量守恒，要么采用另一个关于辐射本质的假设。如果我们假定这一辐射并非量子辐射，而是质量与质子几乎相等的粒子组成的，那么所有关于碰撞的困难都会消失......
所谓查德威克的“基本思路”，其实就是继续相信动量守恒（包括能量守恒）——而博特和约里奥—居里夫妇很可能根本没有意识到这个问题，这导致他们缺乏查德威克那样更精细地分析，对送到眼前的中子“视而不见”。在实验的意义上，他们的工作都相当精彩，倒是查德威克对动量守恒的坚持显得技高一筹——在更广泛的意义上验证了列昂·库珀（Leon Cooper）的说法（也是物理学的共识之一）：动量守恒定律是一个极为深刻的规律，甚至当牛顿力学已经不再适用时，它仍然成立。......假定动量守恒定律是原始公设之一，就可以把整个物理学建立起来。（见《物理学的意义与结构导论》An Introduction of the Meaning and Structure of Physics）
其实对理论家而言，现成的实验或观测事实总是不够的。当上帝把“苹果”送到你面前时，问题的关键在于你信什么或者不信什么。
问：你怎么知道你选择的相信的不会将你引入歧途？
答：赌一把呗......
下一篇：秋风正怀人
28 马德义 陈楷翰 姬扬 徐晓 李天成 张江敏 余党会 武夷山 杨金波 沈律 刘全慧 罗教明 徐传胜 应行仁 李学忠 田云川 余昕 王春艳 ddsers eastHL2008 qidao Veteran11 oceanwen biofans xchen guoyanghuawu quzhizhuo yzqts
该博文允许注册用户评论 请点击登录 评论 (14 个评论)
- [14]王国强
- 1、《物理学的意义与结构导论》An Introduction of the Meaning and Structure of Physics， 此书何在？
2、辈分有点乱啊。。。。
^_^。。。。。。。。。。。。。。 - 博主回复(2014-10-22 13:44)：1.有中译本《物理世界》（上下两册），海洋出版社的，是本老书。
2.可能是汤姆逊、卢瑟福、玻尔、查德威克的关系有点“乱”，玻尔去剑桥本来是拜汤姆逊，结果被老汤支到“大师兄”卢瑟福那里去了。如果把卢瑟福视为玻尔的老师，查德威克就算“小师弟”了。
- [13]王春艳
- “内部相互作用力远远大于合外力”，还是这样定义的条件比较好，就像波粒二象性的条件是粒子运动涉及的空间尺度远大于粒子的德布罗意波长，而趋近于零或近似等于零，这个描述实在没法操作。哈哈
“Noether”，在你这里在表述一下崇敬，名字都这么高大上“NO Ether”…… - 博主回复(2014-10-15 16:31)：在剧烈的物理过程中（比如爆炸、碰撞、反冲），系统内各部分的相互作用是很难测量的。一般用动量定理算冲量再求平均作用力，这就是通过态函数差量规避复杂动力学细节。相较于内力，还是整个过程的时间好测量，用吸收了时间参数的合外力冲量作条件要好一些。
至于诺特，我早就说了嘛，神一样的存在
物理学笔记（4）：玻尔的定态与跃迁
|||
物理学笔记（4）：玻尔的定态与跃迁
一、量子化：定态与跃迁
欲说定态与跃迁，一定要从玻尔谈起......
1913年，曾被J.汤姆逊打发到卢瑟福那儿去的玻尔一口气发表了他的“三部曲”：《论原子和分子的结构》（On the Constitution of Atoms and Molecules）、《单原子核体系》（Systems Containing Only a Single Nucleus）和《多原子核体系》（Systems Containing Several Nuclei）。
在《论原子和分子的结构》（Philos. Mag. 26, 1）中，玻尔写到：
The way of considering a problem of this kind has, however, undergone essential alterations in recent years owing to the development of the theory of the energy radiation, and the direct affirmation of the new assumptions introduced in this theory, found by experiments on very different phenomena such as specific heats, photoelectric effect, Röntgen-rays, & c. The result of the discussion of these questions seems to be a general acknowledgment of the inadequacy of the classical elecrtodynamics in describing the behaviour of system of atomic size.Whatever the alteration in the laws of motion of the electrons may be, it seems necessary to introduce in the laws in question a quantity foreign to the classical electrodynamics, i.e., Planck’s constant, or as it often is called the elementary quantum of action. By the introduction of this quantity the question of the stable configuration of the electrons in the atoms is essentially changed, as this constant is of such dimensions and magnitude that it, together with the mass and charge of the particles, can determine a length of the order of magnitude required.
（近几年来对这类问题的研究途径发生了根本的变化，由于能量辐射理论的发展和这个理论中的新假设从实验取得了一些直接证据，这些实验来自各不相同的现象，诸如比热、光电效应和伦琴射线等等。这些问题讨论的结果看来一致公认经典电动力学并不适于描述原子规模的系统的行为。无论电子运动规律如何变动，看来有必要引进一个明显区别于经典电动力学概念的量到这些规律中来。这个量就叫普朗克常量，或者是经常所称的基本作用量子。通过引进这个量，原子中电子的稳定组态这个问题就发生了根本的变化，比如该常量具有的尺度和大小，结合粒子的质量与电荷，足以确定所需要的线度的数量级。）
在实际的计算过程中，玻尔提出了两个重要的假设：
(1) That the dynamical equilibrium of the systems in the stationary states can be discussed by help of the ordinary mechanics, while the passing of the systems between different stationary states cannot be treated on that basis.（处于定态的系统的动力学平衡可以借助普遍的力学进行讨论，而系统在不同定态之间的过渡则不能在这个基础上处理。）(2) That the latter is followed by the emission of a homogeneous radiation, for which the relation between the frequency and the amount of energy emitted is the one given by Planck’s theory.（后一过程伴随有同类辐射的发射，其频率与释放能量的关系由普朗克理论给出。）
这两条假设现在一般被称为“定态”（stationary state）与“跃迁”（transition or jump）。可能受“大师兄”卢瑟福的影响，玻尔仍然频繁调用了“轨道”（包括stationary orbit）的经典概念，在圆轨道的模型框架下（卢瑟福的核式结构原子模型），玻尔进一步给出了著名的量子化条件，即原子核外电子绕核“公转”的角动量L满足如下关系(mv为电子线动量，R为轨道半径，h为普朗克常量，n为主量子数)：
玻尔的这个量子化条件后来被索末菲推广为多自由度下的量子化通则，又由德布罗意通过德布罗意波在圆轨道上的驻波条件给出解释。量子力学建立后，可以通过薛定谔方程的求解，在主量子数和角量子数“足够大”的情况下（即主量子数和角量子数取极限）得出玻尔量子化条件。
玻尔喜欢用更符合经典味道的”轨道"和"过渡"（passing）指谓定态与跃迁，但并不影响定态跃迁假设和量子化条件刻画了与经典物理完全不同的微观图像——量子化：
（1）玻尔提出“定态”，规定电子处于量子化条件允许的轨道上时不辐射电磁波，实际上是用“强制手段”规避了经典电动力学框架下电子绕核运动辐射电磁波的困难——这种“野蛮”的手法很容易招致不满（汤姆逊、卢瑟福......一干经典大佬），却并不稀奇，比如集合论中的ZFC公理系统就是通过“强制”引入“分类公理”（Axiom schema of specification）规避“真类”（proper class，通俗地讲即自身可以作为元素的“类”，比如所有集合组成的集合）带来的罗素悖论——数学家可以，物理学家为什么不可以？
（2）按玻尔后来（与爱因斯坦的争论中）表述习惯，定态之间的“跃迁”
实际上构造了一个“黑箱”，我们可以通过“初态”和“末态”直接确定辐射或吸收的能量（或反其道而行之，类似于空间中机械运动的位移只与初末位置有关，与实际路径无关），规避了“定态之间如何过渡”这类过于复杂的细节（经典物理意义的），并且这些细节本身（也许暂时地）在实验上是没有意义的，物理学理论只需要刻画实验室里观测到的东西——非常哥本哈根趣味！
（3）量子化条件以及后来的量子化通则在普朗克、爱因斯坦量子与光量子假设的基础进一步强化了微观世界的“碎片化”，即物理量随时间或空间的不连续或离散现象（比如束缚态的能级）。在数学上，这种离散现象与微分方程在有限边界条件的本征值问题密切相关，这与德布罗意的驻波条件契合，也是薛定谔的思考方向。当然这种不连续或离散现象可以通过玻尔的对应原理“平稳地”过渡回符合经典描述的连续世界。
玻尔在上述“半经典”假设基础上构造了他的氢原子模型（可以看成卢瑟福模型的改良版），玻尔氢原子模型与普朗克的黑体辐射定律、爱因斯坦的光电效应方程共同构成了早期量子论（即1925年量子力学建立以前的量子理论）的三个主要模型。普朗克、爱因斯坦、玻尔不断引入的“新假设”及其“古怪”的处理手法在当时的理论物理界激起不小的波澜——有赞许、有抨击、有追随、有修正......
其实在更普遍的意义上（特别是不连续或离散这一点），“量子化”很可能不仅是“20世纪物理学的三条主旋律之一”（杨振宁语，另外两个是“对称”和“相位”），它也许是物理学中一直潜伏的幽灵(按物质结构、相互作用、时空的线索)：从德谟克利特、道尔顿再到分子运动论......，这可以说是物质层次或结构的“量子化”（包括经典意义上电荷的“量子化”）；普朗克、爱因斯坦与玻尔的工作，可以说主要是辐射、能量、作用量......的“量子化”，还有后来的QED、QCD.....；还有高端、大气、上档次的时空量子化或引力量子化......
按照玻尔的“哲学套路”，一贯由经典物理描述的宏观世界也是可以“量子化”的——这取决于观测的空间尺度与时间频率，打些通俗的比方（只是比方！）：比如一堵由标准形状、大小、质量的砖头垒成的墙，不计黏合剂与磨损，墙的高度与总质量一定是单块标准砖厚度和质量的整数倍；动态的电影或动画在时间上有最小的单幅影像，即一帧或一格静止的图像，而一副图像又在空间上存在最小的显像单元——像素.......
换句话说，“一尺之棰，日取其半，万世不竭”在物理上是没有意义的，世界的图像很可能是“簇矢之疾,而有不行不止之时”......
二、状态量与过程量
如果不考虑物理量在空间或时间上是连续的还是离散的，经典物理框架同样也有规避“复杂细节”的办法。
比如经典意义上的热力学主要讨论平衡态（equilibrium state）问题，不用过多考虑偏离平衡态或非平衡态向平衡态过渡的弛豫过程。基于热力学第零、第一、第二定律可以定义刻画平衡态的态函数（state function），对平衡态体系，态函数有确定值，其变化可以由初末态函数决定——定态跃迁的手法！
对刻画自然现象的物理量而言，可以作态函数的物理量称为状态量，而态函数的变化量称为过程量。态函数的判别可以用函数f 构造Pfaff方程:
不妨设i=2，则上式可化为df=Xdx+Ydy=0，当且仅当史瓦西关系成立，即
df=0是具有全微分形式的恰当微分方程，则f为态函数，态函数变化量的积分
与积分路径C无关。
这个数学结论在物理上可以体现为抽象的功能关系：
其中以某些形式的能量作为态函数，可以包括重力势能、引力势能（指经典意义上的引力势能，朗道和栗弗席兹在《场论》中发展了广义相对论框架下的引力势能，具有张量形式）、弹性势能、静电场中的电势能、保守场中的拉格朗日函数和哈密顿函数......如果状态量是具有能量量纲的热力学态函数（内能、焓），过程量还需考虑热量Q。
比如保守场中的势能函数V，在空间三维坐标下有全微分形式
当且仅当
。在我们熟知的重力场或静电场中，作为保守力的重力或静电力做功（重力势能或电势能的变化量）与路径无关，可通过初末状态的重力势能差或电势能差确定。
如果态函数是动能，对应的过程量为合外力所做的功，其中可能有非保守力（比如涡旋电场产生的涡旋电场力）或耗散力（流体粘滞阻力）做功，直接积分比较麻烦，其总功（包括可能的保守力做功）可通过初末状态的动能差确定。
与玻尔的定态跃迁方法类似，经典物理在处理状态量（主要是能量）和过程量（主要是热量和机械功）关系时也尽量规避复杂的细节（动力学意义的），许多具体问题从功能关系入手往往比从动力学方程入手更简便。
一个明显的区别在于：经典物理量在“理论上”是随空间或时间连续分布的。但如同前面提到的，在“实验操作上”，由于观测空间尺度和时间频率的限制，我们只能选择“相信”连续而无法实证之......
也许，世界本来就是量子化的吧？？？
——哥本哈根的，太哥本哈根的！
祝尼尔斯·玻尔生日快乐（1885.10.7）！
Niels Henrik David Bohr
http://blog.sciencenet.cn/blog-217073-833477.html
上一篇：述而不作：双照楼
下一篇：物理学笔记（5）：信动量，得中子
No comments:
Post a Comment