辐射能为主的时期,对称性高,高能,然后对称性破却,能量很大部分变成质量的结合能
曲率的概念是為了度量空間的彎曲程度所產生的數學量,而在高維度的微分幾何學裡,曲率可以看成是度量向量場二次微分的交換程度(這與空間的彎曲程度有關係)。假設
Ricc曲率張量
(1)first Bianchi:
(2)second Bianchi:
(3)
任給
利用局部座標系,我們還可以把
Cartan的流形微分學
假設定理:存在one-forms
我們稱 為connection-one-forms.
為connection-one-forms.
證明:令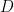 表示
表示 上的黎曼聯絡,且
上的黎曼聯絡,且 定義來自:
定義來自:
那麼利用黎曼聯絡的性質,我們可以得到此結果。
定義
則我們稱矩陣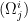 是curvature- 2-form。由於
是curvature- 2-form。由於 在每個點
在每個點 上都是
上都是 的基底,因此我們可以把
的基底,因此我們可以把 寫成
寫成 的表示:
的表示:
其中 為黎曼曲率張量。其中,
為黎曼曲率張量。其中,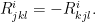
範例:假設 為黎曼曲面,則curvature 2-form為
為黎曼曲面,則curvature 2-form為
其中我們知道曲面的高斯曲率為
註記:所以大家應該可以看到,利用活動標價的方法(Cartan的微分學)可以簡化很多流形上張量的計算。應用的話,大家可以閱讀:曲面的高斯曲率的計算。
《微分几何入门与广义相对论(上册·第二版)》的笔记-第三章 黎曼内稟曲率张量
- 章节名:第三章 黎曼内稟曲率张量
- 2014-09-11 20:43:25
本章内容大致与作者老师所作 http://book.douban.com/subject/1768648/ 第三章相同 适合交叉阅读- 几何学的目的是研究单参变换群下的不变量 此过程开发出来的几何语言常用于描述物理世界在欧氏几何中这些不变量通常由 点 矢量 距离 夹角等概念描述欧氏空间是平直的 矢量沿任何轨迹的平移都不会影响夹角 两条平行线永远也不会相交 但经验发现 欧式几何不足以描述物理世界的规律-在微分几何中 空间不再假设为平直的 每一点上都有局部特殊的矢量空间 这些矢量被定义为该点上的泛函 微积分中的导数算子也被推广到这些矢量及相应的张量上 且可以写作偏微分算子与克氏符的形式在某曲线上的平移由以下包含导数算子的微分方程定义 其中 为曲线的切矢
































No comments:
Post a Comment