为什么第一章如此重要? 各个章节本质上都是极限, 是以函数的形式表现出来的,所以也具有函数的性质。函数的性质表现在各个方面
首先 对 极限的总结 如下
极限的保号性很重要 就是说在一定区间内 函数的正负与极限一致
1 极限分为 一般极限 , 还有个数列极限, (区别在于数列极限时发散的, 是一般极限的一种)
2解决极限的方法如下:(我能列出来的全部列出来了!!!!!你还能有补充么???)
1 等价无穷小的转化, (只能在乘除时候使用,但是不是说一定在加减时候不能用 但是前提是必须证明拆分后极限依然存在) e的X次方-1 或者 (1+x)的a次方-1等价于Ax 等等 。 全部熟记
(x趋近无穷的时候还原成无穷小)
2落笔他 法则 (大题目有时候会有暗示 要你使用这个方法)
首先他的使用有严格的使用前提!!!!!!
必须是 X趋近 而不是N趋近!!!!!!!(所以面对数列极限时候先要转化成求x趋近情况下的极限, 当然n趋近是x趋近的一种情况而已,是必要条件
(还有一点 数列极限的n当然是趋近于正无穷的 不可能是负无穷!)
必须是 函数的导数要存在!!!!!!!!(假如告诉你g(x), 没告诉你是否可导, 直接用无疑于找死!!)
必须是 0比0 无穷大比无穷大!!!!!!!!!
当然还要注意分母不能为0
落笔他 法则分为3中情况
1 0比0 无穷比无穷 时候 直接用
2 0乘以无穷 无穷减去无穷 ( 应为无穷大于无穷小成倒数的关系)所以 无穷大都写成了无穷小的倒数形式了。通项之后 这样就能变成1中的形式了
3 0的0次方 1的无穷次方 无穷的0次方
对于(指数幂数)方程 方法主要是取指数还取对数的方法, 这样就能把幂上的函数移下来了, 就是写成0与无穷的形式了 , ( 这就是为什么只有3种形式的原因, LNx两端都趋近于无穷时候他的幂移下来趋近于0 当他的幂移下来趋近于无穷的时候 LNX趋近于0)
3泰勒公式 (含有e的x次方的时候 ,尤其是含有正余旋 的加减的时候要 特变注意 !!!!)
E的x展开 sina 展开 cos 展开 ln1+x展开
对题目简化有很好帮助
4面对无穷大比上无穷大形式的解决办法
取大头原则 最大项除分子分母!!!!!!!!!!!
看上去复杂处理很简单 !!!!!!!!!!
5无穷小于有界函数的处理办法
面对复杂函数时候, 尤其是正余旋的复杂函数与其他函数相乘的时候,一定要注意这个方法。
面对非常复杂的函数 可能只需要知道它的范围结果就出来了!!!
6夹逼定理(主要对付的是数列极限!)
这个主要是看见极限中的函数是方程相除的形式 ,放缩和扩大。
7等比等差数列公式应用(对付数列极限) (q绝对值符号要小于1)
8各项的拆分相加 (来消掉中间的大多数) (对付的还是数列极限)
可以使用待定系数法来拆分化简函数
9求左右求极限的方式(对付数列极限) 例如知道Xn与Xn+1的关系, 已知Xn的极限存在的情况下, xn的极限与xn+1的极限时一样的 ,应为极限去掉有限项目极限值不变化
10 2 个重要极限的应用。 这两个很重要 !!!!!对第一个而言是X趋近0时候的sinx与x比值 。 地2个就如果x趋近无穷大 无穷小都有对有对应的形式
(地2个实际上是 用于 函数是1的无穷的形式 )(当底数是1 的时候要特别注意可能是用地2 个重要极限)
11 还有个方法 ,非常方便的方法
就是当趋近于无穷大时候
不同函数趋近于无穷的速度是不一样的!!!!!!!!!!!!!!!
x的x次方 快于 x! 快于 指数函数 快于 幂数函数 快于 对数函数 (画图也能看出速率的快慢) !!!!!!
当x趋近无穷的时候 他们的比值的极限一眼就能看出来了
12 换元法 是一种技巧,不会对模一道题目而言就只需要换元, 但是换元会夹杂其中
13假如要算的话 四则运算法则也算一种方法 ,当然也是夹杂其中的
14还有对付数列极限的一种方法,
就是当你面对题目实在是没有办法 走投无路的时候可以考虑 转化为定积分。 一般是从0到1的形式 。
15单调有界的性质
对付递推数列时候使用 证明单调性!!!!!!
16直接使用求导数的定义来求极限 ,
(一般都是x趋近于0时候,在分子上f(x加减麽个值)加减f(x)的形式, 看见了有特别注意)
(当题目中告诉你F(0)=0时候 f(0)导数=0的时候 就是暗示你一定要用导数定义!!!!)
标签:
股票数学模型黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影 一个几何球体上的两个方位线之间的区域。 图片来源:KARTHIK Narayanaswami The region between two Image credit: Karthik Narayanaswami  黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影
在数学中
扩展复数复杂的分析是有用的,因为它们允许零
在几何的黎曼领域是一个黎曼曲面的典型例子,是一个最简单的复流形
扩展复数
扩展复数由的复数C一起∞。
几何上,扩展的复数的组被称为为黎曼球体
加复数可以延长定义为
任何复数
所有非零复数
任何有理函数的
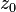  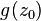 
例如,给定的功能
我们可以定义
当看作是一个复杂的多方面的,合理的功能,其实是全纯函数的黎曼球本身。
直观地说,过渡地图显示如何胶水两架飞机一起,形成黎曼球。
在拓扑上
另一方面,
所有非零复数λ。
C的坐标ξ的另一个副本可以被映射到由
这两个复杂的图表涵盖了投影线。
表明过渡映射ζ= 1 /ξ和ξ= 1 /ζ,如上。
Riemann球形可以作为单位球面上的可视化X
同样,从(0,0,-1)的立体图投影到平面
为了掩盖的单位球,需要两个立体的预测:第一个将覆盖整个领域,除了点(0,0,1)和第二点(0,0,-1)除外。
ζ-坐标和ξ坐标的过渡之间的映射是通过以下方式获得构成一个突起与其他逆。
在此微分同胚,在单位圆中的ζ图,ξ图的单位圆,赤道单位球面的确定。
一个黎曼面不配备任何特定的黎曼度量
在一个给定的保形类,可以使用形对称性找到一个方便性能指标代表。
在黎曼球的情况下,
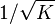
在实际坐标ζ=
最多一个常数因子,这个衡量标准与标准的富比尼研究度量复射影空间(其中的黎曼球就是一个例子)。
相反,,让S表示球体(作为一个抽象的平稳或拓扑流形
任何数学对象的研究,借助于其基团的同构的理解,这意味着从对象到其自身的地图,保存的基本结构的对象。
莫比乌斯变换盈利看作是复杂的投影线的转换。
如果赋予黎曼球面与富比尼-研究公制
在复杂的分析,亚纯函数在复平面上(或任何黎曼曲面上,对这一问题)是一种比F /
G的两个全纯函数
黎曼球在物理学有许多用途。
布朗,詹姆斯和丘吉尔,鲁埃尔(1989年), 格里菲思,菲利普·哈里斯,约瑟夫(1978年)。 彭罗斯,罗杰 鲁丁,瓦尔特(1987年)。 [ Hazewinkel,米歇尔,编辑。 莫比斯转换揭晓 |
分类: 股票数学模型 |


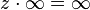
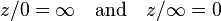

![黎曼球面Riemann <wbr>sphere对冲基金数学模型方法 \ {对齐} \ zeta电= 1 / \十一\ \ [8PT] \ XI = 1 / \泽塔。 \ {对齐}](http://upload.wikimedia.org/math/e/b/b/ebb2d659fa461362aaf1960142b0f066.png)





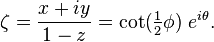
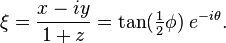
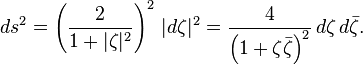
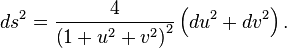

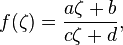

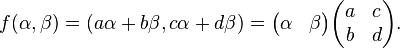
No comments:
Post a Comment