phymath999: 频谱分析是可能证明黎曼猜想的途径;复数放在 ...
phymath999.blogspot.com/2013/01/blog-post_7808.html
轉為繁體網頁
2013年1月18日 - 黎曼猜想是什么(2) 2. 算术基本定理与黎曼zeta函数。 算术基本定理又叫唯一分解定理。这个定理是说,每一个大于1的正整数N都可以写成有限个
phymath999.blogspot.com/2013/01/blog-post_7808.html
轉為繁體網頁
2013年1月18日 - 黎曼猜想是什么(2) 2. 算术基本定理与黎曼zeta函数。 算术基本定理又叫唯一分解定理。这个定理是说,每一个大于1的正整数N都可以写成有限个 轉為繁體網頁
科学网—相对论与黎曼几何-9-平行移动和曲率- 张天蓉的博文
blog.sciencenet.cn/blog-677221-831653.html
轉為繁體網頁
2014年9月29日 - 二维曲面上的平行移动和曲率 根据上节最后得到的“无限小”平行移动公式,理论上便知道了如何将一个矢量的坐标分量改变 ... 相对论与黎曼几何-9-平行移动和曲率 精选 .... 因此,锥面上顶点处的曲率等于无穷大,其余点的曲率为0。
blog.sciencenet.cn/blog-677221-831653.html
轉為繁體網頁
2014年9月29日 - 二维曲面上的平行移动和曲率 根据上节最后得到的“无限小”平行移动公式,理论上便知道了如何将一个矢量的坐标分量改变 ... 相对论与黎曼几何-9-平行移动和曲率 精选 .... 因此,锥面上顶点处的曲率等于无穷大,其余点的曲率为0。轉為繁體網頁
黎曼球面Riemann sphere对冲基金数学模型方法_柳州文铮_ ...
blog.sina.com.cn/s/blog_7f6f656101018wjb.html
轉為繁體網頁
2012年9月24日 - 这个扩展的平面表示扩展的复杂数字 ,即, 复数加一个值∞为无穷大 。 ... 球体与任何紧凑黎曼面,也可能被视为一个射影代数曲线 ,使它代数几何中 ...
blog.sina.com.cn/s/blog_7f6f656101018wjb.html
轉為繁體網頁
2012年9月24日 - 这个扩展的平面表示扩展的复杂数字 ,即, 复数加一个值∞为无穷大 。 ... 球体与任何紧凑黎曼面,也可能被视为一个射影代数曲线 ,使它代数几何中 ...轉為繁體網頁
黎曼度规[http://867107157.qzone.qq.com]
user.qzone.qq.com/867107157/blog/1350126974
轉為繁體網頁
2012年10月13日 - 黎曼度规. 在黑暗的度规中隐藏着鲜为人知的密秘. Kurt Goldel ... 2 0乘以无穷无穷减去无穷( 应为无穷大于无穷小成倒数的关系)所以无穷大都写成 ...
user.qzone.qq.com/867107157/blog/1350126974
轉為繁體網頁
2012年10月13日 - 黎曼度规. 在黑暗的度规中隐藏着鲜为人知的密秘. Kurt Goldel ... 2 0乘以无穷无穷减去无穷( 应为无穷大于无穷小成倒数的关系)所以无穷大都写成 ...轉為繁體網頁
黎曼猜想
159.226.2.2:82/gate/big5/www.kepu.net.cn/gb/.../2_25_1016.htm
希爾伯特回答:“我會先問黎曼猜想是否已經獲得解決了?” 原來他在1900年把這問題 ... 人們早知道下面的調和級數是不收斂(即和是無窮大)。 在1737年左右歐拉引進 ...
159.226.2.2:82/gate/big5/www.kepu.net.cn/gb/.../2_25_1016.htm
希爾伯特回答:“我會先問黎曼猜想是否已經獲得解決了?” 原來他在1900年把這問題 ... 人們早知道下面的調和級數是不收斂(即和是無窮大)。 在1737年左右歐拉引進 ...黎曼曲面_好搜问答 - 奇虎
wenda.haosou.com/search/?q=黎曼曲面&src=tab...pn... - 轉為繁體網頁
黎曼流形和黎曼几何,虽然黎曼面是一个一维复流形。黎曼 ... hold on;n=100;%这个数你自己定,反正到无穷大是不可能了for i=2:n j=1:i-1; j=j(gcd(i,j)==1); plot(j/i,1/i,'r.
wenda.haosou.com/search/?q=黎曼曲面&src=tab...pn... - 轉為繁體網頁
黎曼流形和黎曼几何,虽然黎曼面是一个一维复流形。黎曼 ... hold on;n=100;%这个数你自己定,反正到无穷大是不可能了for i=2:n j=1:i-1; j=j(gcd(i,j)==1); plot(j/i,1/i,'r.黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影

一个几何球体上的两个方位线之间的区域。
图片来源:KARTHIK Narayanaswami
The region between two
Image credit: Karthik Narayanaswami

黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影
在数学中
扩展复数复杂的分析是有用的,因为它们允许零
在几何的黎曼领域是一个黎曼曲面的典型例子,是一个最简单的复流形
扩展复数
扩展复数由的复数C一起∞。
几何上,扩展的复数的组被称为为黎曼球体
加复数可以延长定义为
任何复数
所有非零复数
任何有理函数的 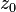

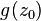

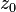

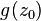

例如,给定的功能
我们可以定义
当看作是一个复杂的多方面的,合理的功能,其实是全纯函数的黎曼球本身。
直观地说,过渡地图显示如何胶水两架飞机一起,形成黎曼球。
在拓扑上
另一方面,
所有非零复数λ。
C的坐标ξ的另一个副本可以被映射到由
这两个复杂的图表涵盖了投影线。
表明过渡映射ζ= 1 /ξ和ξ= 1 /ζ,如上。
Riemann球形可以作为单位球面上的可视化X
同样,从(0,0,-1)的立体图投影到平面
为了掩盖的单位球,需要两个立体的预测:第一个将覆盖整个领域,除了点(0,0,1)和第二点(0,0,-1)除外。
ζ-坐标和ξ坐标的过渡之间的映射是通过以下方式获得构成一个突起与其他逆。
在此微分同胚,在单位圆中的ζ图,ξ图的单位圆,赤道单位球面的确定。
一个黎曼面不配备任何特定的黎曼度量
在一个给定的保形类,可以使用形对称性找到一个方便性能指标代表。
在黎曼球的情况下, 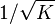
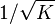
在实际坐标ζ=
最多一个常数因子,这个衡量标准与标准的富比尼研究度量复射影空间(其中的黎曼球就是一个例子)。
相反,,让S表示球体(作为一个抽象的平稳或拓扑流形
任何数学对象的研究,借助于其基团的同构的理解,这意味着从对象到其自身的地图,保存的基本结构的对象。
莫比乌斯变换盈利看作是复杂的投影线的转换。
如果赋予黎曼球面与富比尼-研究公制
在复杂的分析,亚纯函数在复平面上(或任何黎曼曲面上,对这一问题)是一种比F / G的两个全纯函数
黎曼球在物理学有许多用途。
| 本文包含一个列表的引用 |
| 本文列举了它的来源 |
布朗,詹姆斯和丘吉尔,鲁埃尔(1989年),
格里菲思,菲利普·哈里斯,约瑟夫(1978年)。
彭罗斯,罗杰
鲁丁,瓦尔特(1987年)。
[
Hazewinkel,米歇尔,编辑。
莫比斯转换揭晓
古典的幾何學者在討論三維空間中的曲面時,他們留意到曲面上每一點的曲率,都有兩個不同的選擇。比如在一個圓柱面上,一個方向是沿其橫切的圓,另一個則是沿垂直線。高斯在1827發現這兩個曲率的乘積具有驚人的屬性。當我們另曲面在空間變型,只要它沒有拉長縮短,這個積是不變的!後世稱這個積為高斯曲率
[PPT]請點選此處下載。
mathcenter.ck.tp.edu.tw/Resources/Ctrl/ePaper/ePaperOpenFileX.ashx?...
2005年11月15日 - 雙曲幾何給出第一個抽象而與歐氏不一樣的空間,影響到黎曼的工作。 .... 張量滿足等價原理,黎曼曲率使得度量拉長或收縮,正符合他的需要。 ... 物理中的等價原理要求引力的定律與座標的選取無關,黎曼的曲率正正具有這種特性。[PPT]近代幾何的發展 丘成桐香港中文大學數學科學研究所
www.cms.zju.edu.cn/UploadFiles/AttachFiles/20054411421524.ppt
在空間每一點都可以變動的內積,即是說給出了黎曼度量,可以寫作一個張量 。 ... 在一般的黎曼幾何裏,兩點 p 和q 之間可以有超過一條的路徑使得E(x) 是極短的。 ... 在 t 0 ,熱方程的核可以用擾動的方法計算出來,它跟空間的曲率有關,因此指標可由曲率表示, .... 單連通的定義是說在此空間中任何一個閉曲線可以連續收縮成一點。博研联盟.__.2005-几何三十载_百度文库
wenku.baidu.com/view/212730d276eeaeaad1f330d9.html?re=view
2011年3月22日 - 0 在空間每一點都可以變動的內積,即是說給出了黎曼度量, 可以寫作一個張量? i ... 3 在一般的黎曼幾何裏,兩點p 和q 之間可以有超過一條的路徑使得E(x) 是極短的。 ... 0 ,熱方程的核可以用擾動的方法計算出來,它跟空間的曲率有關,因此指標 .... 單連通的定義是說在此空間中任何一個閉曲線可以連續收縮成一點。庞加莱猜想100年 - 欢迎访问科学文化评论 - 中国科学院
sourcedb.scr.cas.cn/zwqkk/.../t20091123_2673455.html
轉為繁體網頁
2009年11月23日 - 高斯的确做过这种测量,但测量误差使他无法做出判断。 ... 在向高维推广时,这缺点更加突出,尤其是当只是“粗线条”地了解图形的时候。 ... 主要的一个是单连通性,也就是球面上任何一个绳圈都可以在球面上连续地变形,最后收缩成一点。 .... 把黎曼轉為繁體網頁
[PDF]to download the PDF file. - 中研院數學研究所
w3.math.sinica.edu.tw/math_media/d232/23201.pdf
Euler-Lagrangian 方程, 即黎曼泛函的. 臨界度量方程。 ... 的初值度量gij(0) 的Ricci 曲率是正的, 則 ... 的解沿著正. Ricci 曲率的方向向內收縮(shrinking); 然 ... 例如在S2科学网—相对论与黎曼几何-15-引力场方程- 张天蓉的博文
blog.sciencenet.cn/blog-677221-843310.html
轉為繁體網頁
2014年11月14日 - 就像是天意安排的,格罗斯曼后来成为黎曼几何专家。 ... 观测者测量直径的时候,轉為繁體網頁
從球面剪取一片曲面,其高斯曲率為正常數。反過來說,局部而言,任何具正常曲率的曲面都是球面的一部分。
類似地,從雙曲曲面剪取的一片,其高斯曲率恒等於負一,而反過來說曲率等於負一的曲面與雙面曲面局部相等。雙曲曲面曾在討論歐氏第五公設時論及算術基本定理與黎曼zeta函數 送交者: 莊銳 2013年01月12日16:19:17 于 [教育學術] 發送悄悄話
黎曼猜想是什麼(2)
2. 算術基本定理與黎曼zeta函數。
算術基本定理又叫唯一分解定理。這個定理是說,每一個大于1的正整數N都可以寫成有限個質數(或者素數)的乘積;這個乘積叫做N的因數分解。N的因數分解中的質數因子可以有重復但是其個數是由這個被分解的正整數確定的,不同整數的分解是不可能相同的。這個定理幾乎有兩千年的歷史。 算術基本定理描述了全體素數是整個大于一的正整數之集合的生成集;就是說從所有素數的集合出發,把所有有限乘積都加進去就得到了所有大于1的正整數之集合。
描述質數之個數的結論叫做素數定理,這個定理根據估計的準確度可以有多種不同的形式。固定任何一個比一大的正整數N,通過簡單的實驗人類很早就知道在一到N之間我們可以期待有少數質數。比如在1到10之間有2,3,5,7這四個質數;佔幾乎五分之二。 這個比例平均地講隨著N的增加在減少,實驗結果告訴我們在一到N之間大概有 M =log(N) 分之一的整數是質數。這里的 log(N) 是類似與常用對數的(以e為底的)自然對數。這個e是繼圓周率pi之後的第二個重要數學常數。用公式表示,通常把從一到N之間的質數個數表示為 pi(N)。這里的 pi 用的是圓周率的同一個符號,但是不是指那個圓周率常數,而是用來表示質數計數函數。 最簡單的素數定理是說 pi(N) 大致等于N 與 log(N) 的商。 這里的大致必須用數學詞匯準確地描繪。 其他精確的素數定理就要給出對這個函數的更精確描寫加上對誤差的估計。
在黎曼之前,高斯對質數計數函數有一個猜測,那就是用現在叫做 高斯的(logarithmic integral) 對數積分函數 li(N) 來代替上面所提到的N與log(N)之商。高斯對後來叫做黎曼zeta函數的那個數學對象已經有過一些研究。1859年,黎曼在他唯一關于數論的研究論文中引進復數作為變量,從而制造出現在叫做黎曼zeta函數的這個特殊函數。黎曼zeta函數是一個以復數為變量的函數,除了一個奇點以外這個函數在整個復數平面上是解析的。這里用的的“解析”一詞,基本上就是微積分中無窮次可微分的意思。
要解釋什麼是黎曼zeta函數,我們還是從如何計算質數的個數說起。 數學發展到前兩個世紀中間的時候,已經有了非常成熟的無窮個數字相加的工具。 其實幾乎兩千年前就有“一尺之棰,日取其半,萬世不竭”的說法。如果把二分之一,四分之一,八分之一,十六分之一,等等一切,一直加起來,可以想象其和為一。 嚴格地說,這就是現代數學系大學高年級里學到的“無窮級數”。定義黎曼zeta函數就必須要用到“無窮級數”與“解析”的概念,所以至少要到大學數學系接近畢業的學人們才可能真正理解黎曼zeta函數的定義。
這里給出在某個場合本人曾經使用過的一個籠統解釋,那就是黎曼zeta函數其實就是把所有的正整數添加必要的附帶數據後然後巧妙地糅合在一起得到的一個函數。不難想象,有關整數的所有一切都被揉在里面了。 因此可以說,這個函數既展示了宇宙的完美無瑕,又顯現出這個世界的雜亂無章。 對于數學家們的問題就是,如何從這個非常復雜的函數里面找到清晰的數學數據。
既然有無窮個質數存在,我們可以比如用每一個正整數的倒數來相加。事實上,所有正整數的倒數相加起來叫做調和級數。調和級數的和仍然是一個無窮大;而這正是黎曼zeta函數中唯一一個奇點的來源。如果把所有正整數的平方的倒數加起來,那麼得到的結果等于那個圓周率的平方除以6。這樣用來研究質數個數的黎曼zeta函數與圓周率也有著緊密的聯系。事實上,所有的數學理論都是緊密地聯系在一起的。作為開端,黎曼zeta函數被定義為所有正整數的其復數變量次方的和,比如我們必須定義2的pi次方是什麼意義。但是這個定義只對復數變量的實數部分大于一的時候有用,然後就要進行進一步的解析延拓把這個函數對所有復數變量都給予定義。除了在復數變量為一的時候為無窮大以外,其他所有復數變量對應的函數值都是有限的。這就是對于什麼是黎曼zeta函數的一個簡單解釋。
相關鏈接︰
| 黎曼猜想是什麼(1) |


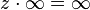
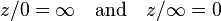

![黎曼球面Riemann <wbr>sphere对冲基金数学模型方法 \ {对齐} \ zeta电= 1 / \十一\ \ [8PT] \ XI = 1 / \泽塔。 \ {对齐}](http://upload.wikimedia.org/math/e/b/b/ebb2d659fa461362aaf1960142b0f066.png)





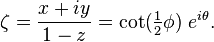
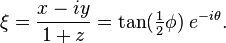
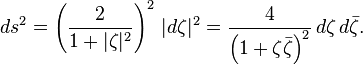
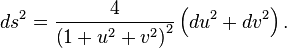

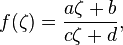

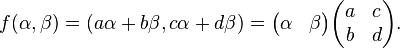
No comments:
Post a Comment