谢邀。
场论的科普工作上,我觉得徐一鸿做了相当不错的工作。参Anthony Zee, Quantum Field Theory in a Nutshell;Feynman也做得很好,参其着的《理性边缘的物理》(QED: The Strange Theory of Light and Matter)。
这是一个不容易的问题,因为场论其实没有什麽新的物理,它是一套系统的方法,把前人的东西简洁表示,然后以此为工具去研究新的问题。没有基本的物理知识(高中或本科程度),跟那人谈场论是没有意思的。不懂物理,场论只是一堆没有意义的数学。而且场论是一种很有趣的东西,读完好像懂,可以跟人谈笑风生,但用到上手却什麽都不会。
例子我主要用谐振子。其实,这个很实用,经典和量子都有解,而且大部分问题都由这个开始,理论家其实除了这个好像什麽也不懂⋯⋯
经典力学
我觉得要懂得量子场论,先要谈谈经典场论。谈经典场论前,先谈经典力学。
假设我们都懂得牛顿力学(不懂的话,场论对你来说没有意思⋯⋯),我们可以用牛顿第二定律得出其运动方程。后来有人发明了能量的概念,再后来有人发明了Lagrangian。需然这些都不是直接可量度的东西,但很有用,只要你写出 ,你可以用最小作用量原理(或Euler-Lagrange方程)得出一样的运动方程。
,你可以用最小作用量原理(或Euler-Lagrange方程)得出一样的运动方程。
这是一个系统:1. 识别系统的自由度;2. 写出系统的Lagrangian;3. 用最小作用量原理得出运动方程。你可能会问,既然我们有牛顿力学,为什麽要发明这个没有新物理意义的东西?答桉是:对于複杂点的系统,写出耦合的运动方程很难,但写出其Lagrangian相对容易,如两质点以一个弹簧连着,这两质点便有耦合,用我们的物理直觉,可自Lagrangian中有一耦合项为 ,再用系统的方法,便知运动方程。(当然这个简单问题,尚可用牛顿透程解决。)
,再用系统的方法,便知运动方程。(当然这个简单问题,尚可用牛顿透程解决。)
经典场论
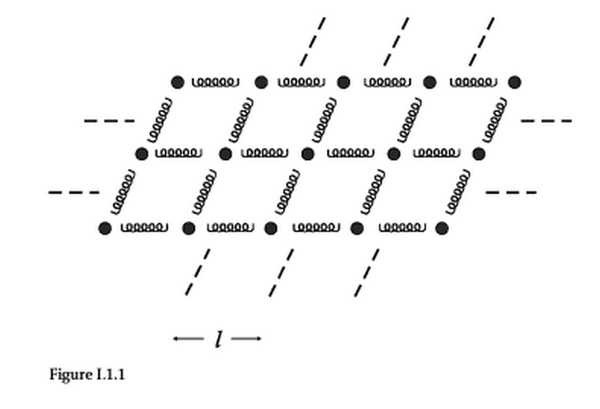
好了,讲完力学,可以讲场论了。上述的问题是单体或少体问题,场论一般处理多体问题。场是什麽?场(field)是空间(实空间、动量空间、或任何奇怪的空间)的函数(参如何让普通人理解物理学中「场」的本质? - 何史提的回答 )。用徐一鸿的方法说,场论处理的问题是一个床垫,找出一函数在床垫不同位置的便化。我们要用Lagrangian density,是场的泛函。同样地,用你的物理直觉,写出了Lagrangian density,再用最小作用量原理便可得运动方程。
经典场论的方程可以足够难解了。学到了这里,你可以跑去学机器学习了。
量子力学
经典力学中的一些量在量子力学便被量子化,有一些量不服从交换定律。这些东西大部分可在经典力学找到对应。可是,在经典力学视为可确定的,在量子力学变为随机,但随机量的平均值仍和经典力学一样。另外,在极限 ,量子力学回归经典力学,此即Correspondence Principle。
,量子力学回归经典力学,此即Correspondence Principle。
量子场论和统计场论
用Schrodinger方程的话,基本可解决很多单体或少体量子问题,但多体问题则需场论。跟经典力学一样,我们可写出其Lagrangian density,亦有系统的方法写出其运动方程,这运动方程跟经典力学的一样,但量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学。
统计场论因其随机性,也有类似的东西,可用泛函积分,用最小自由能解得出平均场解,用linear response求出方差和关联(Kubo方程便和此有关)。古典和量的分别,只是一个用 ,另一用
,另一用 。
。
这好像很简单,但光是上两段,可能足以给一个博士学位,因为经典解也可能是极複杂的。还有,量子场论的微扰複杂得多。幸好我们有伟大的费曼图,简化了不少工作,而每一幅图都代表一项(包含积分式、格林函数/传播子),点的数量代表是微扰阶数。在相对论量子力学中,每一幅图都有物理意义,和某一事件发生的概率有关;在统计场论中,则纯綷代表数式。
微扰通常是小的量,但不幸地,这些费曼图中往往会给出发散的积分。那怎办?我们有重整化,在Lagrangian加些counter-term抵消发散项,而这些发散项可吸至Lagrangian。(参:微积分在微观量子世界还适用吗? - 何史提的回答)
在统计场论中,有一非微扰方法叫重整化群,是对系统作粗粒化处理(有点像在Chrome做zoom out一样),看看Lagrangian中每一项的变化是怎样,决定那些项留或不留。这个肯定和重整化有关,不过小弟还没通透。(参:重整群是不是一种粗粒化处理? - 何史提的回答)
另外,有孤立子的问题,如vortex和Skyrmions的;还有本人不熟悉的拓扑量子场论,什麽Chern-Simons项,很多好东西。
最后想强调这一点:场论本身没有为基本力学加点什麽物理,可是作为系统化的方法,让我们可以跑得跟远,研究更深刻的问题。如果没有物理基础就学场论,则是未学走路就先学跑。当用场论得到结果后,有洞见的物理学家绝对可以不用场论把物理图象清析地描述出来。这有点像基督教中的系统神学,一般信徒是不需要有系统神学训练的都可以过一个有爱心有喜乐的基督徒生命,但系统神学在一个有基础的基督徒可以助他走得更远,他也可深入浅出解析他领受的;但对于连圣经也未读懂的人,系统神学充其量是学术知识,对他能否有一个好的生命没有帮助。 显示全部
场论的科普工作上,我觉得徐一鸿做了相当不错的工作。参Anthony Zee, Quantum Field Theory in a Nutshell;Feynman也做得很好,参其着的《理性边缘的物理》(QED: The Strange Theory of Light and Matter)。
这是一个不容易的问题,因为场论其实没有什麽新的物理,它是一套系统的方法,把前人的东西简洁表示,然后以此为工具去研究新的问题。没有基本的物理知识(高中或本科程度),跟那人谈场论是没有意思的。不懂物理,场论只是一堆没有意义的数学。而且场论是一种很有趣的东西,读完好像懂,可以跟人谈笑风生,但用到上手却什麽都不会。
例子我主要用谐振子。其实,这个很实用,经典和量子都有解,而且大部分问题都由这个开始,理论家其实除了这个好像什麽也不懂⋯⋯
经典力学
我觉得要懂得量子场论,先要谈谈经典场论。谈经典场论前,先谈经典力学。
假设我们都懂得牛顿力学(不懂的话,场论对你来说没有意思⋯⋯),我们可以用牛顿第二定律得出其运动方程。后来有人发明了能量的概念,再后来有人发明了Lagrangian。需然这些都不是直接可量度的东西,但很有用,只要你写出
这是一个系统:1. 识别系统的自由度;2. 写出系统的Lagrangian;3. 用最小作用量原理得出运动方程。你可能会问,既然我们有牛顿力学,为什麽要发明这个没有新物理意义的东西?答桉是:对于複杂点的系统,写出耦合的运动方程很难,但写出其Lagrangian相对容易,如两质点以一个弹簧连着,这两质点便有耦合,用我们的物理直觉,可自Lagrangian中有一耦合项为
经典场论

好了,讲完力学,可以讲场论了。上述的问题是单体或少体问题,场论一般处理多体问题。场是什麽?场(field)是空间(实空间、动量空间、或任何奇怪的空间)的函数(参如何让普通人理解物理学中「场」的本质? - 何史提的回答 )。用徐一鸿的方法说,场论处理的问题是一个床垫,找出一函数在床垫不同位置的便化。我们要用Lagrangian density,是场的泛函。同样地,用你的物理直觉,写出了Lagrangian density,再用最小作用量原理便可得运动方程。
经典场论的方程可以足够难解了。学到了这里,你可以跑去学机器学习了。
量子力学
经典力学中的一些量在量子力学便被量子化,有一些量不服从交换定律。这些东西大部分可在经典力学找到对应。可是,在经典力学视为可确定的,在量子力学变为随机,但随机量的平均值仍和经典力学一样。另外,在极限
量子场论和统计场论
用Schrodinger方程的话,基本可解决很多单体或少体量子问题,但多体问题则需场论。跟经典力学一样,我们可写出其Lagrangian density,亦有系统的方法写出其运动方程,这运动方程跟经典力学的一样,但量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学。
统计场论因其随机性,也有类似的东西,可用泛函积分,用最小自由能解得出平均场解,用linear response求出方差和关联(Kubo方程便和此有关)。古典和量的分别,只是一个用
这好像很简单,但光是上两段,可能足以给一个博士学位,因为经典解也可能是极複杂的。还有,量子场论的微扰複杂得多。幸好我们有伟大的费曼图,简化了不少工作,而每一幅图都代表一项(包含积分式、格林函数/传播子),点的数量代表是微扰阶数。在相对论量子力学中,每一幅图都有物理意义,和某一事件发生的概率有关;在统计场论中,则纯綷代表数式。
微扰通常是小的量,但不幸地,这些费曼图中往往会给出发散的积分。那怎办?我们有重整化,在Lagrangian加些counter-term抵消发散项,而这些发散项可吸至Lagrangian。(参:微积分在微观量子世界还适用吗? - 何史提的回答)
在统计场论中,有一非微扰方法叫重整化群,是对系统作粗粒化处理(有点像在Chrome做zoom out一样),看看Lagrangian中每一项的变化是怎样,决定那些项留或不留。这个肯定和重整化有关,不过小弟还没通透。(参:重整群是不是一种粗粒化处理? - 何史提的回答)
另外,有孤立子的问题,如vortex和Skyrmions的;还有本人不熟悉的拓扑量子场论,什麽Chern-Simons项,很多好东西。
最后想强调这一点:场论本身没有为基本力学加点什麽物理,可是作为系统化的方法,让我们可以跑得跟远,研究更深刻的问题。如果没有物理基础就学场论,则是未学走路就先学跑。当用场论得到结果后,有洞见的物理学家绝对可以不用场论把物理图象清析地描述出来。这有点像基督教中的系统神学,一般信徒是不需要有系统神学训练的都可以过一个有爱心有喜乐的基督徒生命,但系统神学在一个有基础的基督徒可以助他走得更远,他也可深入浅出解析他领受的;但对于连圣经也未读懂的人,系统神学充其量是学术知识,对他能否有一个好的生命没有帮助。 显示全部
qinan wang、知乎用户、Mike Xu 等人赞同
我们的电动老师(他也教量子电动力学)在我们的倒数第二节课上,给我们折腾了电磁场的拉格朗日表述,然后他说要给我们一分钟内讲清楚量子电动力学
然后他说把这个东西量子化就完了,其他都是细节
然后他就讲完了(╯‵□′)╯︵┻━┻
然后他说把这个东西量子化就完了,其他都是细节
然后他就讲完了(╯‵□′)╯︵┻━┻
量子场论是一整套数学方法和物理诠释的总称,你要科普的具体是哪一部分?量子化、重整化、规范场论、对称性、反常乃至温度场论和粒子物理标准模型,这些都是量子场论的组成部分,在概念上相互联系又都独立成章。
专注科普其中一两个不难,一次性全盘托出不大可能。实际上这些题目下大多有成熟的科普先例,也根据读者的背景差异有着不同层次的实现方案。比如‘t Hooft在Scholarpedia的这篇文章Gauge theories,在我看来就是针对本科生的绝佳科普。
专注科普其中一两个不难,一次性全盘托出不大可能。实际上这些题目下大多有成熟的科普先例,也根据读者的背景差异有着不同层次的实现方案。比如‘t Hooft在Scholarpedia的这篇文章Gauge theories,在我看来就是针对本科生的绝佳科普。
放一幅老早画图(回过头看有点不太确切的地方),名字:《理科no料理亭》,大体讲了下场论是咋工作的:
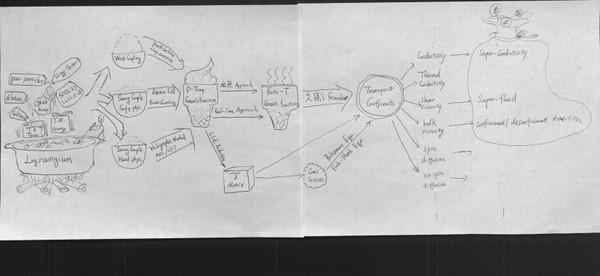
不过这也只能让学过的人看着图叙叙旧。咱还是觉得与普通人讨论场论是挺不智的。因为场论是那种只能说明“有什么用,怎么工作”的东西,而讲不清楚“是什么”。一句“场是什么”就能把你绕进去了。因为场根本就不是物理观测量。学过重整化的都知道,场是要被rescale的,是种说大就大,说小就小的东西。但它又不单纯是种数学工具,所以。。。。能绕开场论就绕开吧。
=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=
终于可以摸着键盘打字了。。
图有点小,解释一下
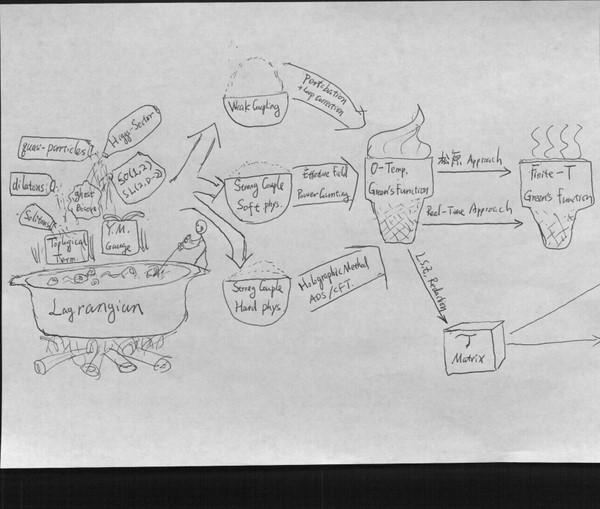
最左边是拉氏量,主要由一些对称原则决定,比如YM。有时要加拓扑项,另一些时候会添一些辅助场,用以揭示一些对偶性。这些系统按照作用强度以及我们的目标分为三类:作用较弱的可以作微扰展开;较强的,但我们只在乎低能情况的,可以按照 展开,这就是低能有效理论;剩下的一种情况就只能格点计算(在高化学势下失败)或者借助Ads/CFT的对偶理论(这个咱不懂)再或者就套各种唯象模型。总之,这些处理手段的目标是取得格林函数。真空下的格林函数作LSZ reduction可以得到截面。介质中的格林函数有两种途径入手。松原方案:虚时格林函数,适用于平衡态,在一些情况下也可以向非平衡作解析延拓。Keldysh方案:实时格林函数,每一个格林函数都写作Keldysh空间下的矩阵,适用于非平衡态。由这些格林函数,通过线性响应理论,可以计算系统的线性输运系数。以电导为例。
展开,这就是低能有效理论;剩下的一种情况就只能格点计算(在高化学势下失败)或者借助Ads/CFT的对偶理论(这个咱不懂)再或者就套各种唯象模型。总之,这些处理手段的目标是取得格林函数。真空下的格林函数作LSZ reduction可以得到截面。介质中的格林函数有两种途径入手。松原方案:虚时格林函数,适用于平衡态,在一些情况下也可以向非平衡作解析延拓。Keldysh方案:实时格林函数,每一个格林函数都写作Keldysh空间下的矩阵,适用于非平衡态。由这些格林函数,通过线性响应理论,可以计算系统的线性输运系数。以电导为例。 ,
, 是外界给系统的微扰,而
是外界给系统的微扰,而 就是系统作出的响应,两者之间线性相关。系数
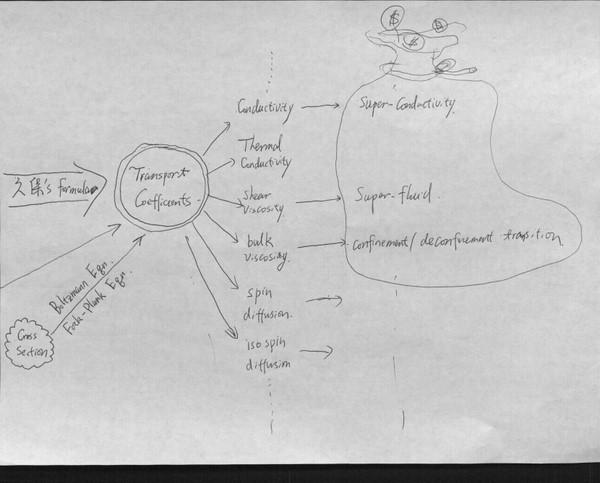
就是系统作出的响应,两者之间线性相关。系数 是系统的内禀属性,与微扰大小无关(与频率还是有关的)。久保方程(Kubo formula)告诉我们:
是系统的内禀属性,与微扰大小无关(与频率还是有关的)。久保方程(Kubo formula)告诉我们:![\sigma(\omega)=\frac 1 \omega\int dtd\mathbf x \theta(t)\langle[\mathbf j(t,\mathbf x),\mathbf j(0)]\rangle e^{-i\omega t}](http://zhihu.com/equation?tex=%5Csigma%28%5Comega%29%3D%5Cfrac+1+%5Comega%5Cint+dtd%5Cmathbf+x+%5Ctheta%28t%29%5Clangle%5B%5Cmathbf+j%28t%2C%5Cmathbf+x%29%2C%5Cmathbf+j%280%29%5D%5Crangle+e%5E%7B-i%5Comega+t%7D) ,而
,而 ,故而右边就是一个两点格林函数,用图表示的话就是幅眼睛一样的图。输运系数另一个求法是把截面带入经典输运方程(Boltzmann或Fock-Plank),把它线性化,然后求得。这条路径就不得不作经典近似了。
,故而右边就是一个两点格林函数,用图表示的话就是幅眼睛一样的图。输运系数另一个求法是把截面带入经典输运方程(Boltzmann或Fock-Plank),把它线性化,然后求得。这条路径就不得不作经典近似了。
总之,图的最左边是系统的底层机理,最右边是宏观观测量,场论只是连接两者的桥梁。说穿了,场论本身的物理与量子力学没有区别,余下的部分全是数学 ,是可借助来形成物理图象的工具。真正有意思的物理在图的两端。当然,图中没有包含所有的宏观量,诸如压强、比热等热力学量的算法因为更简单,没有画在料理亭里。比方如何用场论来回答这个问题呢:水的比热为什么这么大? - 知乎用户的回答。首先要拿到“水”这个系统的拉氏量。然后用虚时方案算配分函数:![Z(\beta)=Z_0(\beta)\exp\left(\sum_{n_l}\frac 1 {n_l !}C_{J=0}[n_l]\right)](http://zhihu.com/equation?tex=Z%28%5Cbeta%29%3DZ_0%28%5Cbeta%29%5Cexp%5Cleft%28%5Csum_%7Bn_l%7D%5Cfrac+1+%7Bn_l+%21%7DC_%7BJ%3D0%7D%5Bn_l%5D%5Cright%29) 。其中,
。其中, 是理想气体的配分函数,
是理想气体的配分函数, 表示所有的泡泡图(bubble diagram),
表示所有的泡泡图(bubble diagram), 是图的vertex数目。有了配分后,取一次对数,作两次偏微分,热容就到手了。我这样答题算回答了那位题主的问题么?不算。因为我只提供了算法,没有提供物理图象,而算法永远不会是“原因”。再比如如果我用这套算法算,发现夸克物质在褪禁闭相的热容要高于在禁闭相的,就能写文章了么?也不行,我还是要提供物理图象:色禁闭禁锢了夸克的自由度,因而降低了体系热容。因而场论只是那个指着月亮的手指,不足为外人道。
是图的vertex数目。有了配分后,取一次对数,作两次偏微分,热容就到手了。我这样答题算回答了那位题主的问题么?不算。因为我只提供了算法,没有提供物理图象,而算法永远不会是“原因”。再比如如果我用这套算法算,发现夸克物质在褪禁闭相的热容要高于在禁闭相的,就能写文章了么?也不行,我还是要提供物理图象:色禁闭禁锢了夸克的自由度,因而降低了体系热容。因而场论只是那个指着月亮的手指,不足为外人道。



不过这也只能让学过的人看着图叙叙旧。咱还是觉得与普通人讨论场论是挺不智的。因为场论是那种只能说明“有什么用,怎么工作”的东西,而讲不清楚“是什么”。一句“场是什么”就能把你绕进去了。因为场根本就不是物理观测量。学过重整化的都知道,场是要被rescale的,是种说大就大,说小就小的东西。但它又不单纯是种数学工具,所以。。。。能绕开场论就绕开吧。
=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=。=
终于可以摸着键盘打字了。。
图有点小,解释一下
最左边是拉氏量,主要由一些对称原则决定,比如YM。有时要加拓扑项,另一些时候会添一些辅助场,用以揭示一些对偶性。这些系统按照作用强度以及我们的目标分为三类:作用较弱的可以作微扰展开;较强的,但我们只在乎低能情况的,可以按照
总之,图的最左边是系统的底层机理,最右边是宏观观测量,场论只是连接两者的桥梁。说穿了,场论本身的物理与量子力学没有区别,余下的部分全是数学 ,是可借助来形成物理图象的工具。真正有意思的物理在图的两端。当然,图中没有包含所有的宏观量,诸如压强、比热等热力学量的算法因为更简单,没有画在料理亭里。比方如何用场论来回答这个问题呢:水的比热为什么这么大? - 知乎用户的回答。首先要拿到“水”这个系统的拉氏量。然后用虚时方案算配分函数:
我做科普喜欢先讲一点儿历史,讲一讲为什么要提出某个概念,是为了解决什么问题,获得了什么结果,包括涉及到的诺贝尔奖
比如我设想的一个提纲,供参考
- 把量子力学相对论化的努力:先讲Klein-Gorden方程,这是薛定谔方程的直接相对论性推广,然后说K-G方程涉及到了时间的二次导;和只涉及到时间一阶导的Dirac方程,以及Dirac的「负能海」、「反粒子」假设(诺贝尔奖:Dirac 方程,正电子,反质子);相对论性量子力学最根本的问题——没法处理粒子产生湮灭的情形,从而自然进入第二部分
- 二次量子化(这个没想好怎么讲,说是太数学化了吧,不讲又无法理解量子力学进入到相对论性情形后的本质变化)
- 如果能讲清楚二次量子化,接下来讲量子场论就是坦途了,场量子化,对易(反对易)关系,这都是自然而然的结论,微扰论讲不讲视受众的情形而定,不过费曼图多少还是得提一下,这个比较直观(诺贝尔奖:泡利不相容原理,量子电动力学)
- 看情形,讲一讲规范对称性(包括电磁场的「额外自由度」的问题以及 C.N. Yang 的八卦)、重整化(主要是代表性的圈图)及其获得的重要成果——兰姆位移、真空自能什么的(诺贝尔奖:兰姆位移,宇称不守恒)
- 到了标准模型这儿,就只能讲概念了,QCD,夸克轻子的种类,中间玻色子,中微子的问题,Higgs机制,基本上就着诺贝尔奖来讲(诺贝尔奖:Gell-Mann,丁肇中,标准模型,对称性破缺,W和Z的发现,tau子,中微子,深度非弹,渐近自由,对称性自发破缺,Higgs粒子)
- beyond SM 随便扯一点儿,以表示大家在 SM 之后也没闲着
 何史提,拉格朗日制造厂 收起
何史提,拉格朗日制造厂 收起
谢邀。
场论的科普工作上,我觉得徐一鸿做了相当不错的工作。参Anthony Zee, Quantum Field Theory in a Nutshell;Feynman也做得很好,参其着的《理性边缘的物理》(QED: The Strange Theory of Light and Matter)。
这是一个不容易的问题,因为场论其实没有什麽新的物理,它是一套系统的方法,把前人的东西简洁表示,然后以此为工具去研究新的问题。没有基本的物理知识(高中或本科程度),跟那人谈场论是没有意思的。不懂物理,场论只是一堆没有意义的数学。而且场论是一种很有趣的东西,读完好像懂,可以跟人谈笑风生,但用到上手却什麽都不会。
例子我主要用谐振子。其实,这个很实用,经典和量子都有解,而且大部分问题都由这个开始,理论家其实除了这个好像什麽也不懂⋯⋯
经典力学
我觉得要懂得量子场论,先要谈谈经典场论。谈经典场论前,先谈经典力学。
假设我们都懂得牛顿力学(不懂的话,场论对你来说没有意思⋯⋯),我们可以用牛顿第二定律得出其运动方程。后来有人发明了能量的概念,再后来有人发明了Lagrangian。需然这些都不是直接可量度的东西,但很有用,只要你写出 ,你可以用最小作用量原理(或Euler-Lagrange方程)得出一样的运动方程。
,你可以用最小作用量原理(或Euler-Lagrange方程)得出一样的运动方程。
这是一个系统:1. 识别系统的自由度;2. 写出系统的Lagrangian;3. 用最小作用量原理得出运动方程。你可能会问,既然我们有牛顿力学,为什麽要发明这个没有新物理意义的东西?答桉是:对于複杂点的系统,写出耦合的运动方程很难,但写出其Lagrangian相对容易,如两质点以一个弹簧连着,这两质点便有耦合,用我们的物理直觉,可自Lagrangian中有一耦合项为 ,再用系统的方法,便知运动方程。(当然这个简单问题,尚可用牛顿透程解决。)
,再用系统的方法,便知运动方程。(当然这个简单问题,尚可用牛顿透程解决。)
经典场论

好了,讲完力学,可以讲场论了。上述的问题是单体或少体问题,场论一般处理多体问题。场是什麽?场(field)是空间(实空间、动量空间、或任何奇怪的空间)的函数(参如何让普通人理解物理学中「场」的本质? - 何史提的回答 )。用徐一鸿的方法说,场论处理的问题是一个床垫,找出一函数在床垫不同位置的便化。我们要用Lagrangian density,是场的泛函。同样地,用你的物理直觉,写出了Lagrangian density,再用最小作用量原理便可得运动方程。
经典场论的方程可以足够难解了。学到了这里,你可以跑去学机器学习了。
量子力学
经典力学中的一些量在量子力学便被量子化,有一些量不服从交换定律。这些东西大部分可在经典力学找到对应。可是,在经典力学视为可确定的,在量子力学变为随机,但随机量的平均值仍和经典力学一样。另外,在极限 ,量子力学回归经典力学,此即Correspondence Principle。
,量子力学回归经典力学,此即Correspondence Principle。
量子场论和统计场论
用Schrodinger方程的话,基本可解决很多单体或少体量子问题,但多体问题则需场论。跟经典力学一样,我们可写出其Lagrangian density,亦有系统的方法写出其运动方程,这运动方程跟经典力学的一样,但量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学。
统计场论因其随机性,也有类似的东西,可用泛函积分,用最小自由能解得出平均场解,用linear response求出方差和关联(Kubo方程便和此有关)。古典和量的分别,只是一个用 ,另一用
,另一用 。
。
这好像很简单,但光是上两段,可能足以给一个博士学位,因为经典解也可能是极複杂的。还有,量子场论的微扰複杂得多。幸好我们有伟大的费曼图,简化了不少工作,而每一幅图都代表一项(包含积分式、格林函数/传播子),点的数量代表是微扰阶数。在相对论量子力学中,每一幅图都有物理意义,和某一事件发生的概率有关;在统计场论中,则纯綷代表数式。
微扰通常是小的量,但不幸地,这些费曼图中往往会给出发散的积分。那怎办?我们有重整化,在Lagrangian加些counter-term抵消发散项,而这些发散项可吸至Lagrangian。(参:微积分在微观量子世界还适用吗? - 何史提的回答)
在统计场论中,有一非微扰方法叫重整化群,是对系统作粗粒化处理(有点像在Chrome做zoom out一样),看看Lagrangian中每一项的变化是怎样,决定那些项留或不留。这个肯定和重整化有关,不过小弟还没通透。(参:重整群是不是一种粗粒化处理? - 何史提的回答)
另外,有孤立子的问题,如vortex和Skyrmions的;还有本人不熟悉的拓扑量子场论,什麽Chern-Simons项,很多好东西。
最后想强调这一点:场论本身没有为基本力学加点什麽物理,可是作为系统化的方法,让我们可以跑得跟远,研究更深刻的问题。如果没有物理基础就学场论,则是未学走路就先学跑。当用场论得到结果后,有洞见的物理学家绝对可以不用场论把物理图象清析地描述出来。这有点像基督教中的系统神学,一般信徒是不需要有系统神学训练的都可以过一个有爱心有喜乐的基督徒生命,但系统神学在一个有基础的基督徒可以助他走得更远,他也可深入浅出解析他领受的;但对于连圣经也未读懂的人,系统神学充其量是学术知识,对他能否有一个好的生命没有帮助。
场论的科普工作上,我觉得徐一鸿做了相当不错的工作。参Anthony Zee, Quantum Field Theory in a Nutshell;Feynman也做得很好,参其着的《理性边缘的物理》(QED: The Strange Theory of Light and Matter)。
这是一个不容易的问题,因为场论其实没有什麽新的物理,它是一套系统的方法,把前人的东西简洁表示,然后以此为工具去研究新的问题。没有基本的物理知识(高中或本科程度),跟那人谈场论是没有意思的。不懂物理,场论只是一堆没有意义的数学。而且场论是一种很有趣的东西,读完好像懂,可以跟人谈笑风生,但用到上手却什麽都不会。
例子我主要用谐振子。其实,这个很实用,经典和量子都有解,而且大部分问题都由这个开始,理论家其实除了这个好像什麽也不懂⋯⋯
经典力学
我觉得要懂得量子场论,先要谈谈经典场论。谈经典场论前,先谈经典力学。
假设我们都懂得牛顿力学(不懂的话,场论对你来说没有意思⋯⋯),我们可以用牛顿第二定律得出其运动方程。后来有人发明了能量的概念,再后来有人发明了Lagrangian。需然这些都不是直接可量度的东西,但很有用,只要你写出
这是一个系统:1. 识别系统的自由度;2. 写出系统的Lagrangian;3. 用最小作用量原理得出运动方程。你可能会问,既然我们有牛顿力学,为什麽要发明这个没有新物理意义的东西?答桉是:对于複杂点的系统,写出耦合的运动方程很难,但写出其Lagrangian相对容易,如两质点以一个弹簧连着,这两质点便有耦合,用我们的物理直觉,可自Lagrangian中有一耦合项为
经典场论

好了,讲完力学,可以讲场论了。上述的问题是单体或少体问题,场论一般处理多体问题。场是什麽?场(field)是空间(实空间、动量空间、或任何奇怪的空间)的函数(参如何让普通人理解物理学中「场」的本质? - 何史提的回答 )。用徐一鸿的方法说,场论处理的问题是一个床垫,找出一函数在床垫不同位置的便化。我们要用Lagrangian density,是场的泛函。同样地,用你的物理直觉,写出了Lagrangian density,再用最小作用量原理便可得运动方程。
经典场论的方程可以足够难解了。学到了这里,你可以跑去学机器学习了。
量子力学
经典力学中的一些量在量子力学便被量子化,有一些量不服从交换定律。这些东西大部分可在经典力学找到对应。可是,在经典力学视为可确定的,在量子力学变为随机,但随机量的平均值仍和经典力学一样。另外,在极限
量子场论和统计场论
用Schrodinger方程的话,基本可解决很多单体或少体量子问题,但多体问题则需场论。跟经典力学一样,我们可写出其Lagrangian density,亦有系统的方法写出其运动方程,这运动方程跟经典力学的一样,但量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学。
统计场论因其随机性,也有类似的东西,可用泛函积分,用最小自由能解得出平均场解,用linear response求出方差和关联(Kubo方程便和此有关)。古典和量的分别,只是一个用
这好像很简单,但光是上两段,可能足以给一个博士学位,因为经典解也可能是极複杂的。还有,量子场论的微扰複杂得多。幸好我们有伟大的费曼图,简化了不少工作,而每一幅图都代表一项(包含积分式、格林函数/传播子),点的数量代表是微扰阶数。在相对论量子力学中,每一幅图都有物理意义,和某一事件发生的概率有关;在统计场论中,则纯綷代表数式。
微扰通常是小的量,但不幸地,这些费曼图中往往会给出发散的积分。那怎办?我们有重整化,在Lagrangian加些counter-term抵消发散项,而这些发散项可吸至Lagrangian。(参:微积分在微观量子世界还适用吗? - 何史提的回答)
在统计场论中,有一非微扰方法叫重整化群,是对系统作粗粒化处理(有点像在Chrome做zoom out一样),看看Lagrangian中每一项的变化是怎样,决定那些项留或不留。这个肯定和重整化有关,不过小弟还没通透。(参:重整群是不是一种粗粒化处理? - 何史提的回答)
另外,有孤立子的问题,如vortex和Skyrmions的;还有本人不熟悉的拓扑量子场论,什麽Chern-Simons项,很多好东西。
最后想强调这一点:场论本身没有为基本力学加点什麽物理,可是作为系统化的方法,让我们可以跑得跟远,研究更深刻的问题。如果没有物理基础就学场论,则是未学走路就先学跑。当用场论得到结果后,有洞见的物理学家绝对可以不用场论把物理图象清析地描述出来。这有点像基督教中的系统神学,一般信徒是不需要有系统神学训练的都可以过一个有爱心有喜乐的基督徒生命,但系统神学在一个有基础的基督徒可以助他走得更远,他也可深入浅出解析他领受的;但对于连圣经也未读懂的人,系统神学充其量是学术知识,对他能否有一个好的生命没有帮助。



No comments:
Post a Comment